
§ 2. Дифференциальное уравнение гармонических колебаний.
Пружинный маятник
Пружинным маятником называется грузик, колеблющийся на пружине.
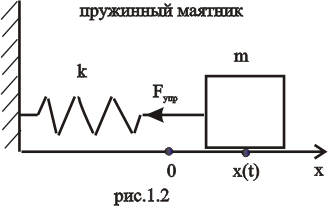 Дифференциальное уравнение – это уравнение, в которое входит неизвестная функция и её производные. Решение дифференциального уравнения - это функция, которая обращает уравнение в тождество (здесь слово «решение» является существительным, оно обозначает функцию – нематериальный объект). Дифференциальное уравнение – это уравнение, в которое входит неизвестная функция и её производные. Решение дифференциального уравнения - это функция, которая обращает уравнение в тождество (здесь слово «решение» является существительным, оно обозначает функцию – нематериальный объект).
Дифференциальные уравнения принято записывать в каноническом виде:
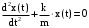 (1.12а) (1.12а)
решения нашего дифференциального уравнения
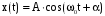 . .
Циклическая частота и период незатухающих колебаний пружинного маятника:
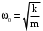 . . 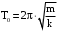
§ 3. Дифференциальное уравнение незатухающих колебаний
физического маятника. Математический маятник.
Гармонические колебания физического маятника
Физическим маятником называют любое твёрдое тело, совершающее под действием силы тяжести колебания вокруг горизонтальной оси, не проходящей через его центр масс.
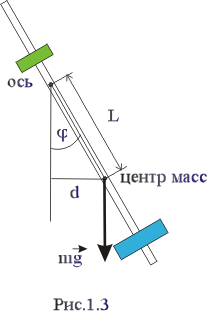 На рис.1.3 маятник отклонён от положения равновесия на угол На рис.1.3 маятник отклонён от положения равновесия на угол 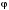 . .
Центр масс – это точка приложения равнодействующей сил тяжести, действующих на маятник - силы 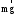 , направленной вертикально вниз , направленной вертикально вниз
(g - ускорение свободного падения).
Выведенный из положения равновесия, маятник будет совершать колебания.
Уравнение движения маятника можно записать,
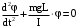
решения :
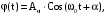
где 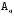 - амплитуда, т. е. наибольший угол, на который отклоняется маятник. - амплитуда, т. е. наибольший угол, на который отклоняется маятник.
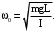 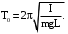
2. Математический маятник
На рис.1.4 изображен математический маятник - физическая модель, которая задается следующим образом. На невесомой и нерастяжимой нити длиной L подвешена материальная точка массой m, на которую с силой rng действует однородное поле силы тяжести. Эта модель применима для описания колебаний тела, размеры которого малы по сравнению с L
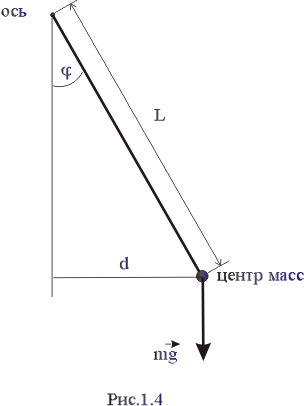 Математический маятник является частным случаем физического. Математический маятник является частным случаем физического.
Для периода малых колебаний математического маятника 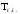 получим следующую формулу: получим следующую формулу:
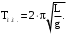 (1.22) (1.22)
Теперь можно ввести термин приведённая длина физического маятника 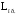 – это длина такого математического маятника, который колеблется с таким же периодом, как и определённый физический маятник – это длина такого математического маятника, который колеблется с таким же периодом, как и определённый физический маятник
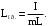
I – момент инерции физического маятника; m – масса физического маятника; L – расстояние от центра масс физического маятника до оси вращения .
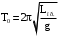 . .
§ 4. Дифференциальное уравнение незатухающих колебаний
заряда в колебательном контуре
Колебательный контур состоит из конденсатора и катушки индуктивности
Приведём уравнение к каноническому виду:
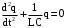 . (1.25) . (1.25)
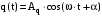 , (1.26) , (1.26)
здесь 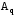 - амплитуда колебаний заряда, максимальный заряд конденсатора. - амплитуда колебаний заряда, максимальный заряд конденсатора.
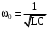 . .
§ 3. Обобщённое уравнение колебаний
Введем обобщенную координату , понимая под ней отклонение любой физической величины от положения равновесия.
Пружинный маятник - 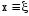 , ,
физический маятник - 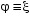 . .
колебательный контур - 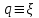 . .
Тогда для всех трех рассмотренных случаев имеем одно и то же дифференциальное уравнение колебательного движения
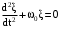 , (1.28) , (1.28)
где 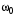 – частота собственных незатухающих колебаний системы. – частота собственных незатухающих колебаний системы.
Пружинный маятник - 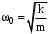 , ,
физический маятник - 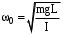 . .
колебательный контур - 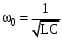 . .
Ясно, что решение обобщённого дифференциального уравнения свободных незатухающих колебаний имеет вид:
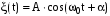 , (1.29) , (1.29)
т. е. является гармонической функцией.
Значит, уравнение
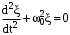 – это дифференциальное уравнение гармонических колебаний. – это дифференциальное уравнение гармонических колебаний.
СЛОЖЕНИЕ КОЛЕБАНИЙ
§ 2. Сложение колебаний одинаковой частоты
и одинакового направления
Пусть складывается два колебания:
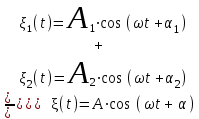 . (2.1) . (2.1)
По теореме косинусов
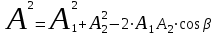 . .
Так как 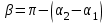 , то , то
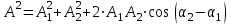 . .
Амплитуда результирующего колебания равна:
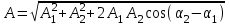 . (2.2) . (2.2)
Очевидно, что начальная фаза результирующего колебания определяется соотношением:
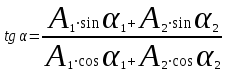 . .
Значит, начальная фаза результирующего колебания равна:
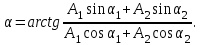 (2.3) (2.3)
Вывод: при сложении колебаний одинаковой частоты и направления результирующее колебание будет совершаться с той же частотой, что и частота складываемых колебаний.
§ 3. Сложение колебаний одного направления
и близких частот
Пусть складывается два колебания с почти одинаковыми частотами, т. е.
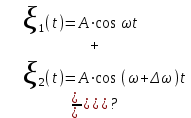 , , 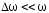 . .
Для количественного анализа сложения колебаний близких частот мы воспользуемся известной тригонометрической формулой:
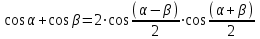 . .
Применяя к нашему случаю, получим:
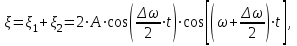
так как 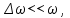 то то
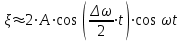 . (2.4) . (2.4)
Г
рафик результирующего колебания – график биений, т. е. почти гармонических колебаний частоты , амплитуда которых медленно меняется с частотой , представлен на рис. 2.3.

Рис. 2.3
Амплитуда биений:
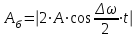 . (2.4а) . (2.4а)
Из-за наличия знака модуля (амплитуда всегда больше нуля) частота, с которой изменяется амплитуда, равна не 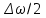 , а в два раза выше – , а в два раза выше – 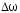 . .
§ 4. Сложение взаимно-перпендикулярных колебаний
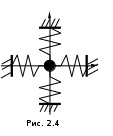
Пусть маленькое тело колеблется на взаимно-перпендикулярных пружинках одинаковой жесткости (рис. 2.4). По какой траектории будет двигаться это тело?
 �X �X
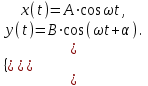 (2.5) (2.5)
Это уравнения траектории в параметрическом виде.
Для получения явной зависимости между координатами x и y надо из уравнений исключить параметр t.
Из первого уравнения:
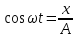 . .
Тогда: 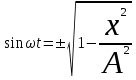 . .
Из второго уравнения:
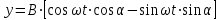 . .
После подстановки сюда полученных выражений для cost и sint получим:
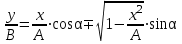 . .
Избавимся от корня:
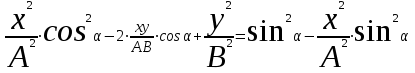 . .
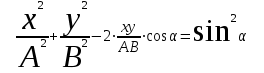 – это уравнение эллипса. (2.6) – это уравнение эллипса. (2.6)
§ 1. Дифференциальное уравнение затухающих колебаний
Пружинный маятник
Рассмотрим колебание грузика, прикрепленного к пружинке, учтем влияние трения на движение грузика (рис. 3.1). На тело действует сила упругости :
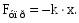
Сила трения препятствует движению.
Дифференциальное уравнение затухающих колебаний пружинного маятника имеет вид:
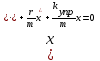 . .
Введем обозначения:
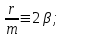 (3.2) (3.2)
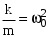 (см формулу (1.13), (см формулу (1.13),
где 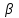 – коэффициент затухания; – коэффициент затухания;
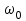 – частота собственных незатухающих колебаний. – частота собственных незатухающих колебаний.
Тогда:
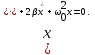 (3.3) (3.3)
Колебания заряда в колебательном контуре
Дифференциальное уравнение затухающих колебаний заряда q на обкладкаконденсатора:
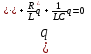 . (3.3а) . (3.3а)
Дифференциальное уравнение, описывающее затухающие колебания любой природы:
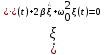 . (3.4) . (3.4)
Для пружинного маятника:
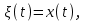
а для колебательного контура:
 . (3.4а) . (3.4а)
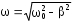 . (3.7) . (3.7)
Предположим, что амплитуда затухающих колебаний убывает по экспоненциальному закону, т.е.
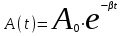 (e=2,71828...), (3.5) (e=2,71828...), (3.5)
тогда решение будем искать в виде:
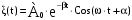 . (3.6) . (3.6)
Выражение для - частоты затухающих колебаний.
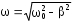 (3.7) (3.7)
§ 2. Период затухающих колебаний
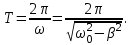 (3.8) (3.8)
§ 3 Логарифмический декремент затухания
В качестве характеристики затухания вводится величина, называемая логарифмическим декрементом затухания.
Логарифмическим декрементом затухания называется натуральный логарифм отношения двух последовательных амплитуд, взятых через период.
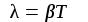 . (3.10) . (3.10)
§ 4. Добротность
Выясним физический смысл логарифмического декремента затухания.
Введем понятие времени релаксации.
Время релаксации – это время , за которое амплитуда (3.6) уменьшилась в e = 2,71раз.
Так как 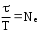 – число колебаний за время , то: – число колебаний за время , то:
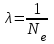 . (3.11) . (3.11)
Логарифмический декремент по величине обратен числу колебаний, за которое амплитуда убывает в е = 2.71 раз.
Характеристикой затухания также является добротность, которая вводится как
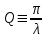 . .
С учетом (3.11):
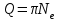 . (3.12) . (3.12)
Добротность пропорциональна числу колебаний, совершаемых системой за время, в течение которого амплитуда уменьшается в е = 2,71… раз.
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
Вынужденные колебания – это колебания, происходящие под действием периодического внешнего воздействия.
§ 1. Дифференциальное уравнение вынужденных колебаний
Пружинный маятник
 
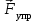
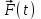
Рис. 4.1
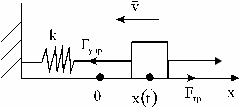
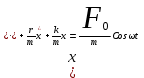 . .
Введем обозначения:
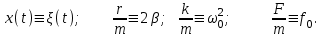
Дифференциальное уравнение, описывающее вынужденные колебания, будет иметь вид:
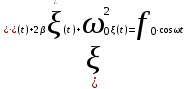 . (4.2) . (4.2)
Колебания заряда в колебательном контуре
В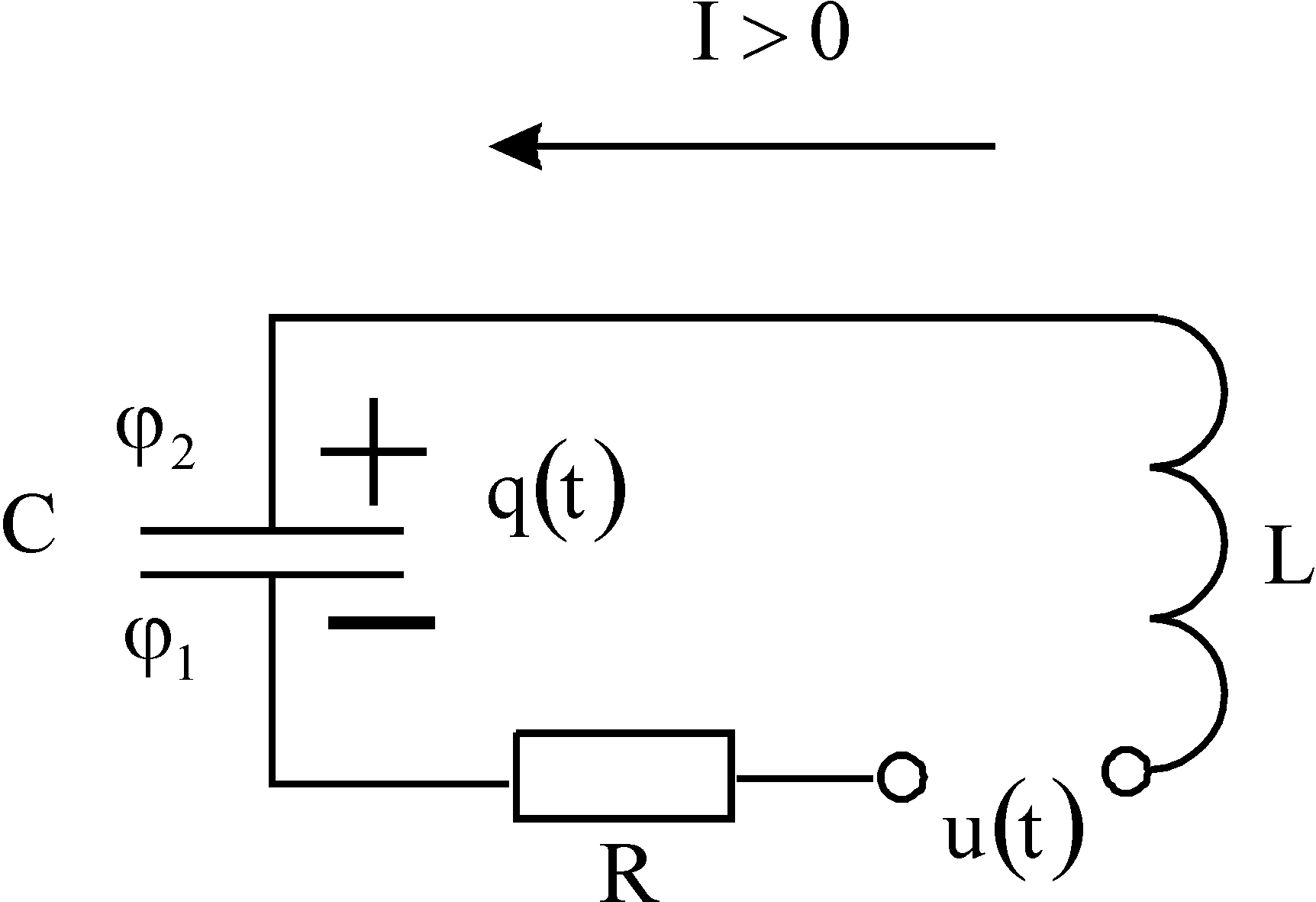 контур включен последовательно источник переменного напряжения, изменяющегося по гармоническому закону: контур включен последовательно источник переменного напряжения, изменяющегося по гармоническому закону:
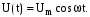
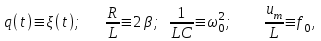
Найдем амплитуду А и начальную фазу вынужденных колебаний. Из рис. 4.3. следует:
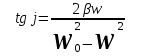 . (4.7) . (4.7)
Амплитуда вынужденных колебаний равна:
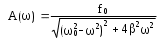 . (4.9) . (4.9)
Амплитуда вынужденных колебаний зависит от частоты вынуждающей силы.
§ 3. Резонанс
Проанализируем, как амплитуда вынужденных колебаний изменяется с изменением частоты внешнего воздействия. При определенной частоте амплитуда достигает максимума. Это явление называется резонансом, а соответствующая частота рез – резонансной.
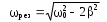 . (4.10) . (4.10)
При 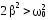 резонанс отсутствует ( резонанс отсутствует (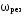 – мнимое число). – мнимое число).
Амплитуда при резонансе
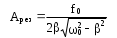 . (4.11) . (4.11)
При 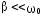 : :
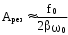 . (4.12) . (4.12)
ЛЕКЦИЯ № 2
§ 1. Упругая волна
Упругая волна – это процесс распространения механических колебаний в упругой среде. Характерное свойство волны – перенос энергии без переноса вещества.
Смещение 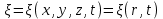 . .
Скорость движения частиц упругой среды – это частная производная от смещения по времени, т. е.
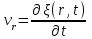 . .
Колебания частиц среды могут совершаться вдоль направления распространения волны или поперек. Поэтому различают продольные и поперечные волны.
Если направление смещения и скорость частицы совпадают с направлением скорости волны, то волна называется продольной. Если они взаимно перпендикулярны, то волна поперечная. В газах и жидкостях могут существовать только продольные волны, в твердых телах – как продольные, так и поперечные.
§ 2. Основные определения для волнового процесса
Фронт волны – поверхность, отделяющая часть пространства, охваченную волновым процессом, от той части, где колебания еще не возникли.
Волновая поверхность – это геометрическое место точек, колеблющихся в одинаковой фазе.
Для плоской волны – волновые поверхности и фронт волны представляют собой плоскости. Для сферической волны – волновые поверхности и фронт волны представляют собой сферы. В общем случае форма волновых поверхностей может быть любой.
Длина волны – это расстояние, на которое распространяется волна за один период колебаний.
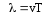 . (5.1) . (5.1)
Так как
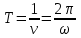 , ,
то
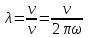 . (5.2) . (5.2)
Волновое число – это величина
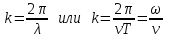 . (5.3) . (5.3)
§ 3. Уравнение плоской волны
Колебания до волновой поверхности, удаленной от начала координат на расстояние x, дойдут через время 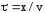 , значит, уравнение волны , значит, уравнение волны
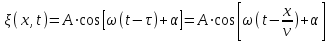 . (5.4) . (5.4)
где 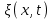 – смещение частиц среды от положения равновесия; – смещение частиц среды от положения равновесия;
х – расстояние от источника до точки наблюдения;
А – амплитуда волны;
– частота колебаний источника;
t – время распространения колебаний;
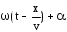 – фаза волны, т. е. аргумент у косинуса в уравнении волны. – фаза волны, т. е. аргумент у косинуса в уравнении волны.
Фаза плоской волны зависит от двух переменных – x и t.
Найдем симметричную форму уравнения плоской волны. Преобразуем уравнение (5.4):
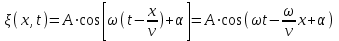 . .
Учтем:
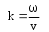 – волновое число. – волновое число.
Тогда:
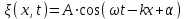 . (5.5) . (5.5)
При такой записи координата х и время t входят в уравнение волны симметрично.
Уравнение плоской волны, распространяющейся в направлении, противоположном оси x, имеет вид:
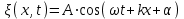 . (5.5а) . (5.5а)
§ 6. Волновое уравнение
Уравнение сферической волны (5.8):
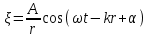 . .
Уравнение любой гармонической волны есть решение волнового уравнения (5.13):
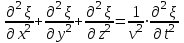 . .
где v – фазовая скорость волны (5.12):
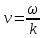 . .
Плотность энергии упругой волны
Плотность энергии упругой волн
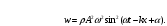
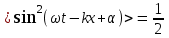 . .
Тогда:
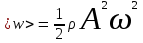 . (6.5) . (6.5)
§ 4. Вектор Умова. Интенсивность
Найдем связь плотности потока энергии с плотностью энергии упругой волны.
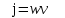 . (6.9) . (6.9)
Интенсивность волны – это среднее по времени от модуля вектора плотности потока энергии:
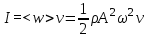 . (6.10а) . (6.10а)
§ 5. Стоячие волны
При наложении двух встречных плоских волн с одинаковой амплитудой возникает колебательный процесс, называемый стоячей волной. При этом переноса энергии не происходит.
Уравнение стоячей волны:
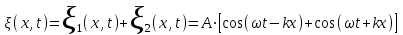 = =
=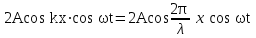 . (6.11) . (6.11)
Амплитуда стоячей волны – это модуль выражения, стоящего перед множителем 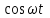 , т е. , т е.
 . (6.12) . (6.12)
Узлы и пучности
Поверхности, где амплитуда колебаний равна нулю, называют узлами стоячей волны. Для узлов:
Следовательно, координаты узлов:
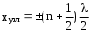 . .
Поверхности, где амплитуда колебаний достигает максимума, называют пучностями стоячей волны.
Для пучностей:
Координаты пучностей:
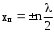 . .
ЛЕКЦИЯ № 3
§ 1. Световые волны
Согласно современным представлениям, свет представляет собой сложное явление: в одних случаях он ведет себя как электромагнитная волна, в других – как поток особых частиц (фотонов). Такое свойство называется корпускулярно-волновым дуализмом (корпускула – частица, дуализм – двойственность).
В этой части курса лекций будем рассматривать волновые явления света.
Световая волна – это электромагнитная волна с длиной волны в вакууме в диапазоне:
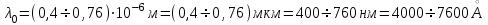 . .
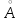 – ангстрем – единица измерения длины. – ангстрем – единица измерения длины. 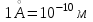 . .
Волны такого диапазона воспринимаются человеческим глазом.
Излучение с длиной волны меньше 400 нм называют ультрафиолетовым, а с большей, чем 760 нм – инфракрасным.
Частота световой волны для видимого света:
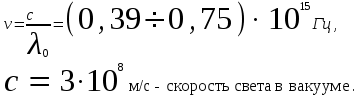
Скорость света совпадает со скоростью распространения электромагнитной волны.
Показатель преломления
Скорость распространения света в среде, как и любой электромагнитной волны равна (см. (7.3)):
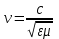 . .
Для характеристики оптических свойств среды вводится показатель преломления. Отношение скорости света в вакууме к скорости света в данной среде называется абсолютным показателем преломления:
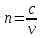 . (8.1) . (8.1)
С учетом (7.3)
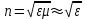 , (8.2) , (8.2)
так как для большинства прозрачных веществ .
Формула (8.2) связывает оптические свойства вещества с его электрическими свойствами. Для любой среды, кроме вакуума, n > 1. Для вакуума n = 1, для газов при нормальных условиях n 1.
Показатель преломления характеризует оптическую плотность среды. Среда с большим показателем преломления называется оптически более плотной. Обозначим абсолютные показатели преломления для двух сред:
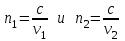 . .
Тогда относительный показатель преломления равен:
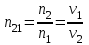 , (8.3) , (8.3)
где 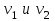 – скорости света в первой и второй среде, соответственно. – скорости света в первой и второй среде, соответственно.
Зависимость показателя преломления от длины волны (или частоты) называется дисперсией.
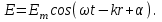 (8.4) (8.4)
Здесь k – волновое число, r – расстояние, отсчитываемое вдоль направления распространения волны, 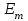 – амплитуда световой волны. Для плоской волны – амплитуда световой волны. Для плоской волны 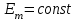 , для сферической убывает как 1/r. , для сферической убывает как 1/r.
Интенсивность световой волны:
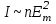 . (8.6) . (8.6)
§ 3. Законы геометрической оптики
Геометрическая оптика – это приближенное рассмотрение распространения света в предположении, что свет распространяется вдоль некоторых линий – лучей (лучевая оптика). В этом приближении пренебрегают конечностью длин волн света, полагая, что 0.
1. Закон прямолинейного распространения света.
Закон прямолинейного распространения света утверждает, что в однородной среде свет распространяется прямолинейно.
2. Закон независимости световых лучей утверждает, что лучи при пересечении не возмущают друг друга. При больших интенсивностях этот закон не соблюдается, происходит рассеяние света на свете.
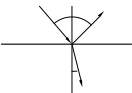
3 и 4. Законы отражения и преломления утверждают, что на границе раздела двух сред происходит отражение и преломление светового луча. Отраженный и преломленный лучи лежат в одной плоскости с падающим лучом и перпендикуляром, восстановленным к границе раздела в точке падения,
(рис. 8.1).
Угол падения равен углу отражения (8.7).
Отношение синуса угла падения к синусу угла преломления равно отношению показателя преломления второй среды к показателю преломления первой (8.8):
 �X �X
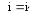 . (8.7) . (8.7)
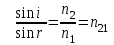 . (8.8) . (8.8)
Рис. 8.1
Закон преломления был открыт в XVII веке В. Снеллиусом и Р. Декартом.
Законы отражения и преломления могут нарушаться в анизотропных средах, т. е. средах, для которых показатель преломления зависит от направления в пространстве.
§ 4. Полное внутреннее отражение
Полное внутреннее отражение наблюдается, если свет падает из оптически более плотной среды на границу раздела с оптически менее плотной средой под углом, большим предельного. Найдем предельный угол полного внутреннего отражения.
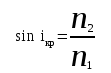 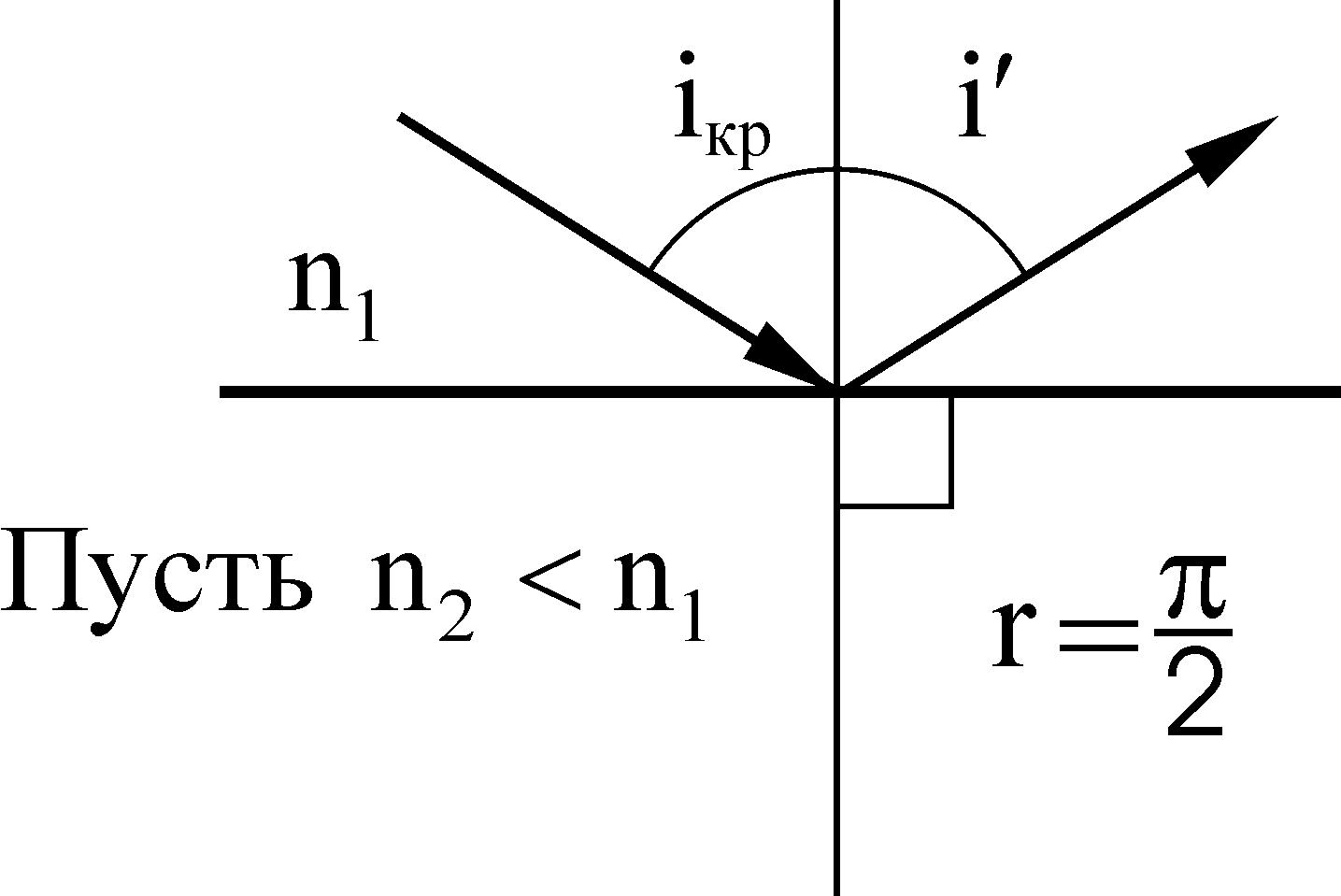 , ,
т. е. 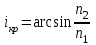 . (8.9) . (8.9)
Угол iкр называют также предельным углом внутреннего отражения.
ИНТЕРФЕРЕНЦИЯ СВЕТА
Интерференцией волн называется наложение волн друг на друга, при котором происходит устойчивое перераспределение энергии в пространстве, вследствие чего образуется так называемая интерференционная картина (от лат. Inter – взаимно, ferio – ударяю). Интерференционная картина световых волн представляет собой чередование темных и светлых участков экрана.
Интерференция наблюдается только от когерентных источников.
§ 1. Интерференция от двух монохроматических источников
одинаковой частоты
Изобразим два точечных источника S1 и S2, излучающих монохроматические световые волны одинаковой частоты . Проанализируем, от чего зависит интенсивность света в точке пространства, удаленной от первого источника на расстояние r1, а от второго – на r2 (рис. 10.1).
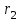
Амплитуда результирующего колебания при сложении колебаний одинаковой частоты и одинакового направления:
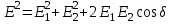 . .
Интенсивность найдем, усреднив это выражение по времени (см. (7.9)):
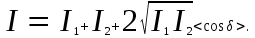 (10.1) (10.1)
§ 2. Когерентность
Когерентностью называется согласованное протекание колебательных или волновых процессов.
Когерентными источниками называют такие источники, которые дают волны одинаковой частоты и для фиксированной точки пространства разность фаз колебаний, возбуждаемых волнами, остается постоянной.
Таким образом, при наложении когерентных световых волн происходит перераспределение светового потока в пространстве, в результате чего в одних местах возникают максимумы, а в других – минимумы интенсивности.
§ 3. Условия максимума и минимума на разность фаз
Это условие, как видно из (10.2), заключается в следующем:
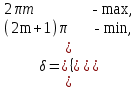 m = 0, 1, 2, … (10.3) m = 0, 1, 2, … (10.3)
§ 4. Оптическая разность хода
здесь 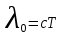 – длина световой волны в вакууме. – длина световой волны в вакууме.
Произведение показателя преломления на геометрический путь называют оптическим путем.
Оптической разностью хода называют величину:
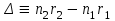 . (10.4) . (10.4)
Тогда оптическая разность хода и разность фаз интерферирующих волн связаны соотношением:
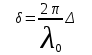 . (10.5) . (10.5)
 
(10.6)
(10.7)
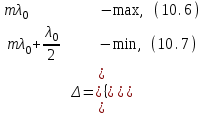 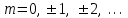
Следовательно, если оптическая разность хода равна целому числу длин волн в вакууме или четному числу полуволн, то при интерференции двух волн наблюдается максимум интенсивности. Это и есть условие максимума при интерференции (10.6). Соответственно, условие минимума при интерференции (10.7) читается так: если оптическая разность хода равна полуцелому числу длин волн в вакууме или нечетному числу полуволн, то наблюдается интерференционный минимум интенсивности. В этих формулах целое число m называется порядком интерференционного максимума или минимума.
§ 6. Способы получения когерентных источников
Когерентные источники получают, разделив световую волну, идущую от одного источника, на две. Две части одной волны когерентны между собой. Существуют разные способы получения когерентных световых источников.
Опыт Юнга
Т
омас Юнг наблюдал интерференцию от двух источников, прокалывая на малом расстоянии (d 1 mm) два маленьких отверстия в непрозрачном экране. Отверстия освещались светом от солнца, прошедшим через малое отверстие в другом непрозрачном экране. Схема опыта Юнга приведена на рис. 10.4
Интерференционная картина наблюдалась на экране, удаленном на расстоянии L 1 м от двух источников. Так, впервые в истории, Т. Юнг определил длины световых волн (используя формулу (10.8)).
При использовании лазера в качестве источника света необходимость в экране 1 отпадает.
Итак, в методе Юнга используется механическое деление световой волны
с помощью экрана с двумя отверстиями. Эти отверстия являются действительными источниками света.
§ 1. Интерференция при отражении от прозрачных пластинок
Интерференция в тонких пленках наблюдается довольно часто. Например, окраска тонких прозрачных пленок, цветные разводы на тонких пленках бензина или масла на поверхности воды. Рассмотрим, как образуется интерференционная картина в тонких пленках.
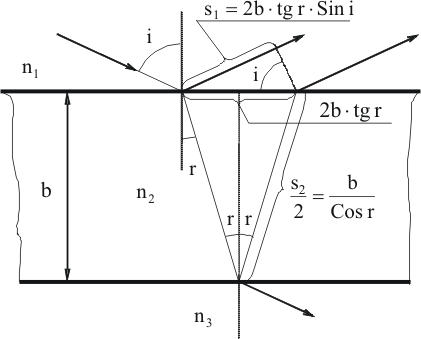
Рис. 11.1
Луч света, падающий на прозрачную пластинку, частично отражается и частично преломляется. Преломленный луч, отражаясь от нижней поверхности пластинки, идет к верхней грани и преломляется на ней второй раз. Таким образом получаются два луча.
Условие максимума интенсивности в отраженном свете (10.6) с учетом (11.3) имеет вид:
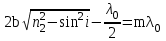 . (11.4) . (11.4)
Условие минимума:
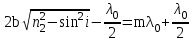 , m = 0,1,2, … (11.5) , m = 0,1,2, … (11.5)
Из этих условий следует два возможных варианта интерференционной картины.
1. Если толщина пленки постоянна (b = const) и пластинка освещается рассеянным светом, то интерференционная картина будет представлять собой линии одинакового наклона. Каждому определенному углу наклона световых лучей i будет соответствовать своя линия, т. е. своя окружность. С помощью линий равного наклона можно контролировать плоскопараллельность тонких пленок. Если интерференционная картина будет представлять собой окружность, то пластинка плоскопараллельна.
2. Если пластинка освещается параллельными лучами (i = const), но толщина пластинки не постоянна, то интерференционная картина будет представлять собой линии одинаковой толщины. При освещении пластинки белым светом каждой толщине соответствует своя окраска.
ЛЕКЦИЯ № 4
§ 1. Явление дифракции волн
Дифракция (от лат. difractus – преломленный) в первоначальном смысле – огибание волнами препятствий, в современном, более широком смысле – любые отклонения при распространении волн от законов геометрической оптики (см. лекцию № 8).
Причина дифракции, как и интерференции, – суперпозиция волн, которая приводит к перераспределению интенсивности.
§ 2. Принцип Гюйгенса – Френеля
Принцип Гюйгенса – Френеля:
Каждая точка, до которой доходит волна, служит источником вторичных сферических волн, огибающая которых дает положение волнового фронта в следующий момент времени (Х. Гюйгенс, 1678 г.).
Амплитуда результирующей волны в любой точке пространства может быть найдена как результат интерференции всех вторичных волн, с учетом их фаз и амплитуд (О. Френель, 1818 г.).
§ 4. Дифракция Френеля на круглом отверстии
Пусть на пути сферической световой волны, испускаемой источником S, расположен непрозрачный экран с круглым отверстием радиуса r0 (рис. 12.3). Если отверстие открывает четное число зон Френеля, то в точке P будет наблюдаться минимум, так как все открытые зоны можно объединить в соседние пары, колебания которых в точке P приблизительно гасят друг друга.
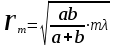 . (12.3) . (12.3)
Расстояние a примерно равно расстоянию от источника до преграды, расстояние b – от преграды до точки наблюдения P.
§ 5. Дифракция Фраунгофера на щели
Следовательно, условие минимума при дифракции Фраунгофера на щели имеет вид:
 (12.5) (12.5)
условие максимума при дифракции Фраунгофера на щели будет иметь вид:
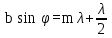 . (12.6) . (12.6)
§ 1. Дифракция на дифракционной решетке
Дифракционная решетка – это совокупность большого числа одинаковых щелей, отстоящих друг от друга на одно и то же расстояние. Расстояние d между соответственными точками соседних щелей называют периодом решетки:
d = a + b,
здесь а – ширина непрозрачного промежутка; b – ширина щели.
Условие главного максимума для дифракционной решетки будет иметь следующий вид:
dsin = mλ, m = 0, 1, 2, … (13.1)
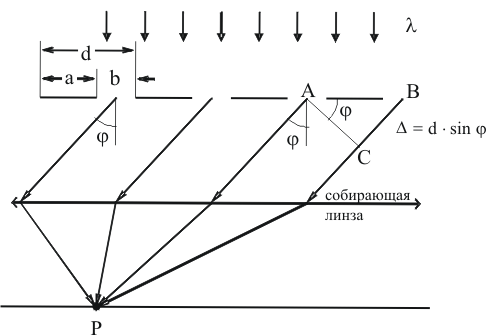
Рис. 13.1
Целое число m называют порядком максимума.
Для условий минимумов интенсивности от дифракционной решетки анализ дает следующие результаты:
 (13.2) (13.2)
– это условие минимума для щели (12.5);
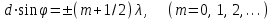 (13.3) (13.3)
– это условие главного минимума для решетки.
§ 4. Разрешающая сила дифракционной решетки
Разрешающая сила характеризует свойство дифракционной решетки разделять излучения, близкие по длине волны. Разрешающей силой или разрешающей способностью, называют безразмерную величину:
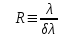 . (13.12) . (13.12)
Здесь – минимальная разница в длинах волн соседних спектральных линий, при которой эти линии еще можно наблюдать раздельно.
В результате получим:
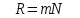 . (13.13) . (13.13)
ПОЛЯРИЗАЦИЯ СВЕТА
Поляризацией света называется совокупность явлений волновой оптики,
в которых проявляется поперечность электромагнитных волн. Если колебания светового вектора 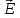 упорядочены, то свет называется поляризованным. упорядочены, то свет называется поляризованным.
§ 1. Естественный и поляризованный свет

У естественного света направления векторов 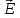 у разных цугов у разных цугов
различны.
Световая волна – это электромагнитная волна, у которой вектор всегда перпендикулярен направлению распространения. Электромагнитная волна,
у которой вектор Е колеблется в одной плоскости, называется плоско поляризованной (рис. 14.1). Естественный свет (см. § 2, лекция № 10) – это смесь огромного числа цугов. Каждый цуг поляризован, т. е. вектор Е совершает колебания в одной плоскости, но направления векторов Е разных цугов различны. Поэтому естественный свет неполяризован, у него отсутствует какое-либо упорядочение направлений колебаний вектора Е (рис. 14.2).

Плоскость, в которой колеблется вектор Е называется плоскостью поляризации.
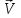
Рис. 14.1 Рис. 14.2
Плоско поляризованная электромагнитная волна представлена на рис. 14.1.
Упорядоченность колебаний может заключаться в том, что вектор Е поворачивается вокруг луча, одновременно пульсируя по величине. В результате конец вектора описывает эллипс. Такой свет называется эллиптически поляризованным. Если конец вектора описывает окружность, то свет называется поляризованным по кругу.
§ 3. Закон Малюса
З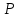 акон Малюса устанавливает связь между интенсивностями света, прошедшего через два последовательных поляризатора. акон Малюса устанавливает связь между интенсивностями света, прошедшего через два последовательных поляризатора.
Р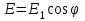 ис. 14.5 ис. 14.5
Поляризаторы предполагаются идеальными, т. е. после прохождения через такой поляризатор свет становится плоскополяризованным.
Поставим на пути естественного света два одинаковых поляроида, оси пропускания которых развернуты друг относительно друга на угол
(рис. 14.5).
Вектор 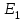 любого цуга световой волны после первого поляроида будет параллелен PP любого цуга световой волны после первого поляроида будет параллелен PP 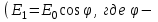 любой угол между плоскостью колебаний вектора любой угол между плоскостью колебаний вектора 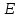 и осью поляроида РР). Этот поляроид называют поляризатором, так как после него естественный свет стал плоскополяризованным. и осью поляроида РР). Этот поляроид называют поляризатором, так как после него естественный свет стал плоскополяризованным.
Второй поляроид служит для анализа характера поляризации света и называется анализатором.
 После второго поляроида останется лишь вектор После второго поляроида останется лишь вектор 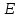 , параллельный PP его оси пропускания: , параллельный PP его оси пропускания:
 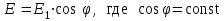 . .
Так как интенсивность света пропорциональна среднему значению квадрата напряженности электрического поля (7.9):
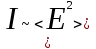 , ,
то после первого поляроида:
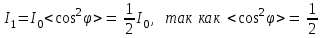 . .
После второго поляроида интенсивность будет
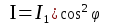 , (14.1) , (14.1)
где I1 – интенсивность перед вторым поляроидом. Полученное соотношение между интенсивностями носит название закона Малюса.
Закон Малюса читается так: интенсивность света, прошедшего через поляризатор и анализатор, равна интенсивности света, прошедшего через поляризатор, умноженной на квадрат косинуса угла между плоскостями пропускания колебаний поляризатора и анализатора.
Если I1 выразить через I0, то закон Малюса примет вид:
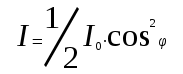 . (14.2) . (14.2)
Если , то I = 0 и поляризаторы называются скрещенными.
Закон Малюса строго выполняется лишь для идеальных поляроидов: поляризатора и анализатора.
Если поляризатор частично пропускает свет с вектором 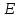 , перпендикулярным оси пропускания, то после него свет будет частично поляризован. , перпендикулярным оси пропускания, то после него свет будет частично поляризован.
В этом случае идеальный анализатор при PP, параллельной PP, пропустит свет интенсивностью Imax, а при PP, перпендикулярной PP, – свет интенсивностью Imin.
Степенью поляризации частичного поляризованного света называется величина
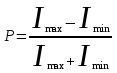 . (14.3) . (14.3)
При идеальном поляризаторе Imin = 0 и P = 1, свет плоскополяризован.
При естественном свете 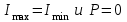 , свет неполяризован. , свет неполяризован.
ЛЕКЦИЯ № 1 |
 Скачать 1.62 Mb.
Скачать 1.62 Mb.