Физика. Лекции. Лекция1 Предмет механики
 Скачать 1.62 Mb. Скачать 1.62 Mb.
|
|
§ 2. Закон Био-Савара-Лапласа Экспериментально магнитное поле, создаваемое током, изучали французкие ученые Ж. Био и Ф. Савар, результаты этих исследований математически оформил их соотечественник П. Лаплас.  . (8.2) . (8.2)Единица измерения магнитной индукции в системе СИ– «тесла» (Тл).. Графическое изображение магнитного поля Магнитное поле графически изображается, как и электрическое, с помощью линий магнитной индукции (магнитных силовых линий). Линии магнитной индукции: 1) замкнуты, так как в природе нет магнитных зарядов; 2) вектор В направлен по касательной к линии магнитной индукции; 3) густота линий магнитной индукции пропорциональна модулю векто- ра В. § 3. Примеры применения закона Био-Савара-Лапласа В этом параграфе мы применим закон Био-Савара-Лапласа для расчета магнитного поля в двух простейших случаях: в центре кольца с током и в случае прямого проводника с током. Магнитное поле в центре кольца с током Таким образом, магнитная индукция в центре кольца равна: 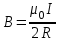 . (8.3) . (8.3) Вектор магнитной индукции направлен перпендикулярно плоскости кольца, направление вектора 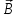 определяется по правилу правого винта для кольцевого тока: винт установить перпендикулярно плоскости кольца и поворачивать по направлению тока в кольце, направление поступательного движения винта покажет направление вектора определяется по правилу правого винта для кольцевого тока: винт установить перпендикулярно плоскости кольца и поворачивать по направлению тока в кольце, направление поступательного движения винта покажет направление вектора 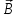 . . Магнитный диполь Магнитное поле кольца, по которому течет ток, вне кольца можно рассматривать как поле магнитного диполя. Такой диполь характеризуется дипольным магнитным моментом. Модуль дипольного магнитного момента:  , (8.4) , (8.4)где S – площадь контура с током. Для бесконечного проводника 1 = 0, 2 = , сos1 - сos2 = 2, следовательно, из (8.6) получим:  . (8.7) . (8.7)ЛЕКЦИЯ № 6 (раздел 2)(лек. №9 «КЛФ, ч.2») Циркуляция и поток вектора магнитной индукции Вектор магнитной индукции – физическая величина, характеризующая магнитное поле точно так же, как напряженность электрического поля характеризует электрическое поле. Для вектора магнитной индукции можно ввести понятие циркуляции по замкнутому контуру и потока вектора В через поверхность. Циркуляция вектора В – это интеграл вида: 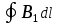 . .Интеграл берется по замкнутому контуру. Найдем циркуляцию вектора 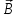 по контуру в виде окружности, по контуру в виде окружности, 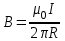 , ,где R – радиус окружности. Циркуляция вектора В вдоль силовой линии равна: 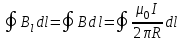 . .Длина элемента дуги окружности, как известно из определения радианной меры угла, равна:  . .Теорема о циркуляции: Циркуляция вектора В по произвольному, замкнутому контуру равна алгебраической сумме токов, охватываемых контуром, умноженной на  , т.е. , т.е.  (9.2) (9.2)Знак у силы тока выбирается в соответствии с правилом правого винта: выбирается направление обхода контура, если направление тока совпадает с направлением смещения правого винта, который вращается по направлению обхода контура, берется знак «+», в противном случае – знак «-». Как видим, циркуляция вектора магнитной индукции по замкнутому контуру может отличаться от нуля, в то время как циркуляция вектора напряженности электростатического поля по замкнутому контуру всегда равна нулю (см. (3.14)). Векторное поле, у которого циркуляция по замкнутому контуру отлична от нуля, называют вихревым или соленоидальным. Если циркуляция по замкнутому контуру всегда равна нулю, то поле называют потенциальным. Таким образом, электростатическое поле потенциально, а магнитное – соленоидально. Соленоид – провод, навитый на цилиндрический каркас. На один метр длины – n витков:  , ,где N – число витков на длине l (см. рис. 9.5).  (9.3) (9.3)Направлено 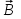 вдоль оси соленоида, в соответствии с правилом правого винта. вдоль оси соленоида, в соответствии с правилом правого винта.Магнитное поле тороидаТороид – провод, навитый на тор (бублик). Магнитное поле тороида:  (9.4) (9.4)Вне тора поле 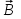 = 0 (докажите!) = 0 (докажите!)При r/R 1, B = 0nI, (сравните с (9.3). (9.5) ЛЕКЦИЯ № 7, (раздел 1) (лек. №10 «КЛФ, ч.2») Закон Ампера. Рамка с током в магнитном поле § 1. Закон АмпераИсточником магнитного поля является электрический ток (движущийся электрический заряд) и, по аналогии с электрическим полем, можно ожидать, что магнитное поле действует на другой ток с силой, пропорциональной силе тока и магнитной индукции поля. Обобщив опытные данные о действии магнитного поля на проводник с током, французский ученый Ампер установил, что на элемент тока в магнитном поле действует сила  , (10.2) , (10.2)Направление которой, определяется по правилам векторного произведения (см. рис. 10.1). 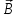 Если векторы dl и B взаимно перпендикулярны, можно использовать более удобное правило – правило левой руки: левую руку располагают так, чтобы силовые линии вектора магнитной индукции входили в ладонь, а четыре пальца были направлены по току, тогда отогнутый большой палец покажет направление силы, действующий на проводник с током. Силу, действующую на проводник с током в магнитном поле называют силой Ампера. Для того, чтобы найти силу Ампера, действующую на проводник сложной формы или больших размеров, нужно разбить проводник на элементы тока и затем найти векторную сумму сил, действующих на элементы тока. Сила Лоренца. Движение заряженной частицы в магнитном поле § 2. Сила Лоренца Электрический ток – это направленное, упорядоченное движение свободных зарядов (см. лекцию 6, § 1). Если на проводник с током в магнитном поле действует сила Ампера, то объясняется это тем, что на каждый движущийся заряд в магнитном поле действует сила, которую называют силой Лоренца –. Исходя из выражения для силы Ампера, определим силу, действующую на каждый заряд, т.е. силу Лоренца.  § 4. Движение заряженной частицы в однородном магнитном поле Рассмотрим случай, когда вектор 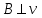 (см. рис. 11.3). (см. рис. 11.3).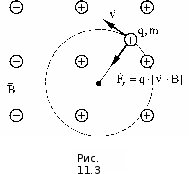 Линии индукции направлены за чертеж, В = const. Линии индукции направлены за чертеж, В = const.Радиус окружности можно получить, подставляя выражение (11.4) для нормального ускорения в формулу (11.3):  (10.5) (10.5)Время, за которое частица совершает один оборот, называется периодом обращения. Длина окружности, как известно, 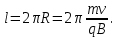 Скорость движения по окружности постоянна, поэтому период обращения:  Лекция 5 § 1. Поток вектора магнитной индукции 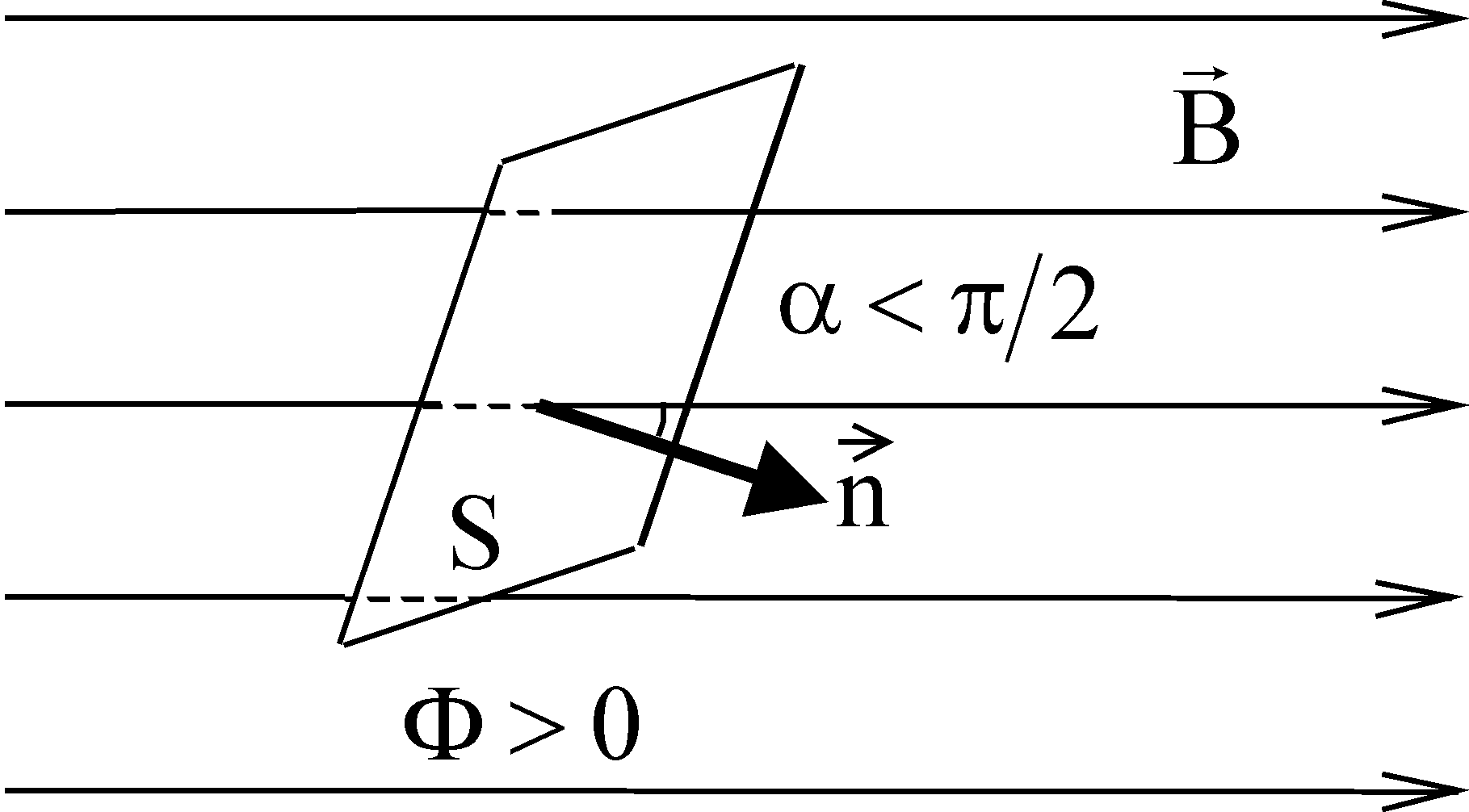 Рис. 9.7 Поток вектора магнитной индукции определяется аналогично потоку вектора напряженности электрического поля. Для однородного магнитного поля (рис. 9.7) поток вектора B определяется формулой (9.6). 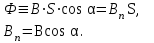 (9.6) (9.6)Единица измерения потока вектора магнитной индукции Ф имеет наименование «вебер», Вб:  . .§ 1. Явление электромагнитной индукции Закон Фарадея Если по замкнутому проводнику течет ток, значит в нем действует ЭДС. Найдем ЭДС, возникающую в контуре, изображенном на рис. 12.1, где одна сторона поступательно движется в магнитном поле вдоль направляющих проводящих шин перпендикулярно силовым линиям (см. рис. 12.1)  Рис. 12.1 На рис. 12.1 магнитное поле B направлено от нас. Если мы тянем подвижную сторону со скоростью v, то на заряд +q действует сила Лоренца Можно считать, что заряд под действием силы Лоренца проходит расстояние l, равное длине подвижного проводника, при этом работа, совершаемая магнитным полем, равна: 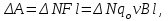 где 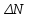 – число носителей заряда, прошедших чрез сечение, l – длина проводника, qо – заряд одного носителя. – число носителей заряда, прошедших чрез сечение, l – длина проводника, qо – заряд одного носителя.Работу, совершаемую магнитным полем, можно представить как работу, совершаемую источником ЭДС, возникающей в проводнике, движущемся в магнитном поле. Величину ЭДС найдем, воспользовавшись определением ЭДС (6.11): 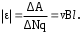 За время dt площадь прямоугольной рамки, ограниченной проводящими шинами и подвижным проводником, увеличивается на 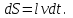 Соответственно, магнитный поток увеличивается на 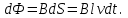 Сравнивая с выражением для ЭДС, видим, что  . .Теперь, исходя из направления нормали, выберем направление положительного обхода контура также согласно правилу «правого винта»: за направление положительного обхода принимается направление вращения правого винта, при котором он перемещается в направлении нормали. 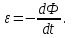 (12.1) (12.1)ЭДС, возникающая в контуре при изменении потока вектора магнитной индукции через поверхность, ограниченную контуром, называют ЭДС электромагнитной индукции. Значение ее определяется формулой (12.1), которая является математическим выражением закона Фарадея. Направление ЭДС индукции удобно определять по правилу Ленца, которое утверждает: индукционные токи всегда направлены так, чтобы компенсировать изменения потока вектора магнитной индукции, приводящие к их появлению. Сумму магнитных потоков, связанных с каждым витком, называют потокосцеплением или полным потоком: 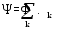 (12.2) (12.2)Используя (12.2), ЭДС электромагнитной индукции (12.1) можно выразить через скорость изменения потокосцепления :  (12.3) (12.3)§ 2. Индуктивность, явление самоиндукции Электрический ток, текущий в контуре, согласно закону Био-Савара-Лапласа создает магнитное поле, вектор магнитной индукции В которого пропорционален силе тока I. Магнитный поток Ф, в соответствии с определением (9.7) и формулой (9.8), пропорционален вектору магнитной индукции В. Следовательно, магнитный поток Ф и полный магнитный поток (потокосцепление) должны быть пропорциональны силе тока, текущему в контуре (см. рис. 12.3).  (12.4) (12.4)К  оэффициент про-порциональности между потокосцеплением и током называют индуктивностью контура. оэффициент про-порциональности между потокосцеплением и током называют индуктивностью контура. Индуктивность не зависит от силы тока, а определяется только размерами, конфигурацией контура, магнитными свойствами окружающей контур среды.  Если ток в контуре зависит от времени (I = I(t)), то магнитный поток тоже будет переменным (Ф = Ф(t)) и возникает ЭДС индукции. ЭДС индукции, возникающую за счет изменения тока в контуре, называют ЭДС самоиндукции сам:  . .Если L = const, то 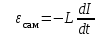 . (12.5) . (12.5)Индуктивность соленоида:  (12.6) (12.6)§ 3. Энергия магнитного поля Р  ассмотрим соленоид, по которому течет ток I. При размыкании цепи ЭДС самоиндукции поддерживает ток в соленоиде и совершает положительную работу за счет энергии, накопленной в соленоиде. Найдя работу, можно найти энергию соленоида. ассмотрим соленоид, по которому течет ток I. При размыкании цепи ЭДС самоиндукции поддерживает ток в соленоиде и совершает положительную работу за счет энергии, накопленной в соленоиде. Найдя работу, можно найти энергию соленоида.По катушке L течет ток I, поддерживаемый источником . При размыкании цепи (ключ переводим в положение 2) ток I поддерживается за счет ЭДС самоиндукции сам, возникающей за счет уменьшения тока I. В соответствии с (6.11), работа, совершаемая сам по перемещению заряда dq, равна:  Здесь мы сначала выразили dq через силу тока I, использовав определение (6.1), а затем применили (12.3), выразив сам через скорость изменения потокосцепления . Вся работа: 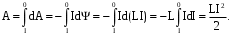 Эта работа равна энергии, накопленной в соленоиде: 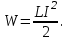 (12.7) (12.7)При уменьшении тока уменьшается магнитное поле соленоида, следовательно, формула (12.7) дает значение энергии магнитного поля в объеме соленоида. Выразим энергию магнитного поля через характеристику поля – магнитную индукцию В. Для этого ток I, используя (9.3), выразим через индукцию B, индуктивность L подставим из (12.6): В = 0nI, I = В/(0n), L = 0n2V. Тогда:  . (12.8) . (12.8)Введем понятие плотности энергии магнитного поля, точно так же, как соотношением (5.12) введена плотность энергии электрического поля. Тогда, с учетом (12.8), для плотности энергии магнитного поля в вакууме имеем:  (12.9) (12.9)§ Уравнения Максвелла 1. Уравнения Максвелла выражают связи между характеристиками электромагнитного поля и связывают электрические и магнитные поля с зарядами и токами. 2. Д.К. Максвелл обобщил эмпирические законы электрических и магнитных явлений и, дополнив их гипотезой о том, что переменное электрическое поле порождает магнитное, получил систему уравнений, составляющих основу электродинамики покоящихся сред. 3. Система уравнений Максвелла может быть записана как в интегральной форме:  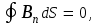 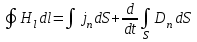 , , ЛЕКЦИЯ № 1 § 1. Понятие о колебательных процессах Колебаниями называются движения или процессы, обладающие той или иной повторяемостью во времени. В зависимости от физической природы, колебания подразделяют на механические, электромеханические, электромагнитные и т. д. В зависимости от характера воздействия, оказываемого на колеблющуюся систему, различают: 1) свободные или собственные колебания – это такие колебания, которые происходят в системе после того, как она была выведена из положения равновесия и предоставлена самой себе. Свободные колебания бывают затухающими и незатухающими; 2) вынужденные колебания – это такие колебания, в процессе которых колеблющаяся система подвергается воздействию внешней периодически изменяющейся силы (например, раскачивание качелей). Уравнение гармонических колебаний Амплитуда. Фаза. Круговая частота Гармонические колебания – это такие колебания, при которых колеблющаяся величина x изменяется со временем по закону синуса либо косинуса:  , или , или  где x(t) – отклонение или смещение колеблющейся величины от положения равновесия; A – амплитуда, т. е. наибольшее отклонение от положения равновесия (амплитуда всегда положительна); (t + ) – фаза колебания – это аргумент периодической функции, определяющей смещение; – начальная фаза, т. е. значение фазы в начальный момент времени (при t = 0); – круговая, или циклическая частота. При изменении аргумента косинуса либо синуса (т. е. фазы) на 2 эти функции возвращаются к прежнему значению. Найдем промежуток времени T, в течение которого фаза гармонической функции изменяется на 2, откуда: (t + T) + = t + + 2, или T = 2.  . (1.2) . (1.2)Время Tодного полного колебания называется периодом колебания. Частотой называют число колебаний в единицу времени, т. е. величину, обратную периоду: 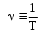 . (1.3) . (1.3)Единица измерения частоты – герц (Гц), 1 Гц = 1 с-1.  , то , то . . Круговая частота – это скорость изменения фазы со временем. График гармонического колебания (1.1) представлен на рис. 1.1. |
