ворд. Документ Microsoft Word. Литература по теме Тема Основы системного анализа Вопрос Системный подход и системный анализ

• Название: Литература по теме Тема Основы системного анализа Вопрос Системный подход и системный анализ
• Дата: 25.04.2022
• Размер: 0.56 Mb.
• Имя файла: Документ Microsoft Word.docx
• Тип: Литература; #495220
• страница: 6 из 9

Тема 6. Модели принятия решений на основе функции полезности

 

Цели изучения темы:

·     изучить подходы к задачам принятия решений на основе функции полезности.

 

Задачи изучения темы:

·     познакомиться с концепцией функции полезности;

·     познакомиться с подходами к построению функции полезности;

·     познакомиться с подходами к принятию решений на основе применения функции полезности.

 

Успешно изучив тему, Вы:

Получите представление о:

·     способах определения функции полезности;

·     возможных условиях принятия решения.

 

Будете знать:

·     основные виды аппроксимирующих функций;

·     основные критерии принятия решений в условиях риска и условиях неопределенности.

 

Вопросы темы:

1.  Понятие функции полезности.

2.  Принятие решений в условиях риска.

3.  Принятие решений в условиях неопределенности.

 

Модели и методы, рассматривавшиеся в предыдущей теме, относились к случаям, когда изучаемая система работала в так называемых условиях определенности. Под условиями определенности понимают такие условия, когда поведение системы (и, в частности, значения каждого ее показателя качества) полностью предсказуемы. Однако на практике такое поведение наблюдается далеко не всегда и приходится применять другие методы оценивания и принятия решений.

 

Вопрос 1. Понятие функции полезности.

 

Подход к оценке системы на основе теории полезности использует метод свертывания векторного критерия в скалярный. Свертывание, в отличие от других методов, производится на основе предпочтений лица, принимающего решение. Полезность исхода операции определяется как действительное число, приписываемое исходу операции и характеризующее его предпочтительность по отношению к другим. Зная возможные альтернативы с их показателями полезности можно построить функцию полезности, с помощью которой можно производить сравнения и принимать решения. Функция полезности представляет собой ограниченную функцию  , определенную на множестве альтернатив  такую, что  , когда альтернативы   и   неразличимы ( ), т.е., когда нельзя отдать предпочтение ни тому, ни другому исходу, и  , когда альтернативы   предпочтительнее альтернативы   ( ).

В теории полезности доказывается, что при вполне естественных допущениях относительно предпочтений лица, принимающего решение, существует функция полезности в виде отображения упорядоченного множества альтернатив Аво множество действительных чисел. Предпочтения лица, принимающего решение, формулируются в виде аксиом. Поскольку различные лица, принимающие решения, имеют разные предпочтения, то разные аксиоматики приводят к разным функциям свертки, и, следовательно, функция полезности не единственная. Причина заключается в том, что отсутствуют определения нулевой полезности, единицы полезности и шкалы полезности (выбор их произволен).

Согласно теории полезности при выполнении всех пяти аксиом существует функция полезности, однозначно определенная на множестве всех альтернатив с точностью до монотонного строго возрастающего линейного преобразования (т.е., полезность определяется в шкале интервалов).

В зависимости от типа показателей исходов операции функция полезности может быть либо непрерывной, либо дискретной.

Функцию полезности называют прямой, если большему значению показателя исхода операции соответствует большее значение функции полезности (т.е., тем исход полезнее), и обратной в противном случае.

Для определения функции полезности необходимо:

·     выявить показатели исходов операции;

·     определить множество допустимых исходов операции;

·     определить показатели полезности исходов операции.

 

Все известные способы определения функции полезности носят приближенный характер и могут быть сгруппированы следующим образом.

Анализ влияния исхода операции на операцию более высокого уровня иерархии основывается на моделировании и предполагает включение оцениваемой системы как элемента в старшую систему и рассмотрении влияния исследуемой системы на функционирование старшей (включающей) системы. Например, для оценивания значения системы связи (передачи команд) по сети оповещения необходимо рассмотреть весь процесс перевода системы управления в состояние повышенной боевой готовности. Если удастся определить такую зависимость, то полученная функция будет функцией полезности. Достоинством способа является его высокая объективность, недостатком – трудность реализации.

Способ определения функции полезности с использованием метода экспертных оценок основан на предпочтительном использовании практического опыта и знаний людей по отношению к формальным методам. Поэтому этим подходам отдается предпочтение, и они интенсивно разрабатываются. При любом способе проведения экспертизы в ней выделяются этапы:

·     упорядочение множества исходов операции по их предпочтительности  ;

·     определение полезности каждого исхода и проверка полученных оценок на непротиворечивость путем сравнения оценок предпочтительности полезности исходов;

·     устранение противоречий в оценках путем корректировки или варианта упорядочения исходов или показателей полезности или того и другого вместе.

 

Способ определения функции полезности на основе аппроксимации заключается в следующем. При рассмотрении исходов конкретной операции отыскиваются характерные точки, соответствующие, например, экстремумам функции полезности, а неизвестные значения между ними заменяются какой-либо известной зависимостью. Вид аппроксимации выбирается на основе имеющихся сведений или качественных соображений о показателях полезности исходов. На практике могут применяться многоступенчатые или другие сложные аппроксимации функции полезности. Наиболее простыми являются одноступенчатое, косинусоидальное и треугольное представления функции полезности (рис. 13).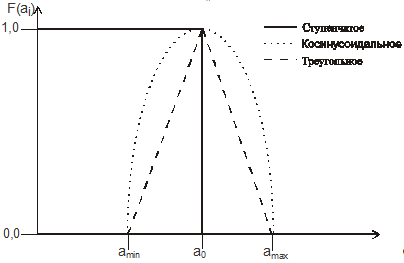

 



 

Рис. 13. Примеры представлений функций полезности

 

Одноступенчатое представление может применяться для операции, в которых показателем исхода является своевременность выполнения работ, например, выплавки шихты, подачу управляющего сигнала системы наведения противоракеты в системе ПВО, подготовка презентации. В этом случае под исходом понимается фактическое время завершения процесса (готовности результата). Если точка   означает некоторый характерный или критический момент процесса, то при   полезность равна 1, при   полезность равна 0.

Косинусоидальное и треугольное представления функции полезности могут применяться для операций, в которых показателем исхода операции является ее временной интервал, например, подготовка телеконференции в ЛВС. Слишком ранняя доступность материалов может привести к ненужной перегрузке и ограничению пропускной способности сети для других приложений, а задержка готовности может привести к тому, что некоторые пользователи ЛВС могут отказаться от участия в телеконференции. Характерными точками в данном случае будут минимально и максимально допустимые значения времен готовности   и   вместе с плановым сроком  . В зависимости от предпочтений лица, принимающего решение, функция полезности может быть представлена либо фрагментом косинусоиды, либо треугольником, построенным по этим точкам.

 

Вопрос 2. Принятие решений в условиях риска.

 

Условиями риска называют такие условия функционирования систем, когда результат выполняемых системой операций (действий, работ) характеризуется как вероятностный. Однозначность соответствия между системами и исходами в вероятностных операциях нарушается. Например, в силу ненадежности сетевого оборудования время передачи сообщений может меняться случайным образом по известному закону. Очевидно, оценивать системы, функционирующие в условиях риска, таким же образом, как в детерминированных системах, нельзя.

Эффективность функционирования систем в условиях риска чаще всего находится через математическое ожидание функции полезности на множестве исходов отдельных операций. Поясним применение процедуры оценивания на следующем примере.

Пусть необходимо оценить варианты оборудования локальной вычислительной сети с целью выбора наилучшего. Полезность оборудования определяется обеспечиваемая им интенсивность обмена сообщениями между пользователями, функция полезности строится экспертным путем (в зависимости от числа передаваемых в сети сообщений). Исходные данные для оценивания представлены в таблице:

 

i
1	60 40 20	0,30 0,50 0,20	0,8 0,5 0,1
2	60 40 20	0,25 0,60 0,15	0,8 0,5 0,1

 

Здесь

i – номер варианта сетевого оборудования;

- возможные варианты производительности (число передаваемых в течение некоторого времени сообщений);

 – вероятность того, что в сети i будет передано  сообщений;

 - значение функции полезности передачи по сети   сообщений.

 

Расчет математического ожидания функции полезности   для каждого варианта i сетевого оборудования производим согласно определению математического ожидания: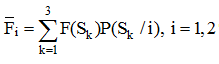

 



 

Подставляя значения из таблицы, получаем: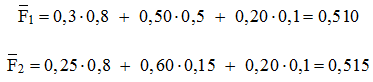

 



 

Из полученных оценок заключаем, что предпочтение следует отдать варианту сетевого оборудования № 2.

Кроме оптимизации в среднем в вероятностных операциях в теории принятия решений рассматриваются и используются и другие критерии оценки систем:

·     максимум вероятности случайного события;

·     максимум степени вероятностной гарантии достижения результата не ниже требуемого уровня;

·     минимум среднего квадрата отклонения результата от требуемого;

·     минимум дисперсии результата;

·     максимум вероятностно-гарантированного результата;

·     минимум среднего (байесовского) риска (минимум средних потерь).

 

Вопрос 3. Принятие решений в условиях неопределенности.

 

Специфические черты многих сложных систем не позволяют при решении ряде задач свести их ни к детерминированным, ни к вероятностным и, следовательно, применить методы, применяемые в этих случаях. Описание условий неопределенности, удобное с точки зрения применения методов оценивания, можно представить в виде таблицы:

 

i			…
1			…
2			…
…	…	…	…	…
n			…

 

Здесь

i– идентификатор системы (операции);

- состояние внешней среды;

- эффективность системы i для состояния внешней среды  .

 

Для оценивания альтернатив в теории принятия решения используются различные критерии. К числу наиболее часто используемых относятся критерии:

·     среднего выигрыша;

·     Лапласа;

·     осторожного наблюдателя (критерий Вальда);

·     максимакса;

·     пессимизма-оптимизма (критерий Гурвица);

·     минимального риска (критерий Сэвиджа).

 

Критерии основаны на разных презумпциях, поэтому выбор того или иного во многом определяется субъективными предпочтениями аналитика или лица, принимающего решение,. Поясним сказанное на примере применения двух из вышеназванных критериев.

Пусть необходимо оценить пять программных продуктов для защиты от вирусных атак. Известны значения эффективности применения каждой программы по отражению каждого вида атак, общее число видов атак равно 4.

 

	1	2	3	4
1	0,4	0,3	0,4	0,2
2	0,2	0,4	0,5	0,2
3	0,1	0,4	0,5	0,3
4	0,4	0,4	0,3	0,2
5	0,5	0,4	0,3	0,3

 

Каждая i-ая строка таблицы содержит значения эффективности   применения i-ой программы,  , для всех видов вирусов, а каждый j-ый столбец – значения эффективности   применения для борьбы с j-ым вирусом,  , всех программ.

Для определения наилучшего варианта (в данном случае, антивирусной программы) в первых пяти вышеперечисленных критериях используется правило, в соответствии с которым для этого наилучшего варианта должно выполняться:

 



 

где

 – значение обобщенного критерия эффективности применения i-ой программы.

Вместе с тем, каждый из этих критериев использует свое правило для нахождения этого значения.

 

В частности, согласно критерию Вальда значения критерия для каждого i-го варианта   находятся как минимально возможные значения критерия для всех вариантов j-ой обстановки (что объясняет причину второго названия критерия – осторожного наблюдателя):

 



 

В нашем примере минимальная эффективность применения каждой из программ для всех вирусов будет соответственно:

 



 

Таким образом, по критерию Вальда следует считать наилучшей пятую программу как имеющую наибольшее значение критерия из всей совокупности.

Смысл критерия Сэвиджа состоит в выборе варианта, минимизирующегопотериэффективности при наихудших условиях. Для оценки систем на основе данного критерия матрица эффективности должна быть преобразована в матрицу потерь (риска). Каждый элемент матрицы потерь определяется как разность между максимальным и текущим значениями оценок эффективности в столбце

 



 

В нашем примере для матрицы потерь имеем (значения максимумов по столбцам   равны соответственно 0,5; 0,4; 0,5; 0,3):

 

	1	2	3	4
	0,1	0,1	0,1	0,1
	0,3	0,0	0,0	0,1
	0,4	0,0	0,0	0,0
	0,1	0,0	0,2	0,1
	0,0	0,0	0,2	0,0

 

По матрице потерь определяются значения критерия как:

 



 

Для нашего примера:

 



 

Очевидно, что целесообразно выбирать тот вариант системы, который обеспечит минимум потерь, т.е., для которого:

 



 

В нашем случае минимальные потери должны быть в случае выбора первой программы, для которой  .

Оба рассмотренных критерия принадлежат к числу осторожных критериев.

 

Выводы:

1.  Переход от задачи многокритериальной оптимизации к однокритериальной может осуществлять на основе концепции функции полезности. Функция полезности представляет собой ограниченную функцию, определенную на множестве альтернатив, отображающую упорядоченное множество альтернатив во множество действительных чисел.

2.  Для практического построения функции полезности применяются различные подходы. Одним из наиболее употребительных является способ определения функции полезности на основе аппроксимации.

3.  Реальные условия функционирования сложных систем не позволяют однозначно предсказать их поведение в какой-либо момент в будущем. В зависимости от возможности или невозможности вероятностного описания поведения системы различают условия риска и условия неопределенности. Для каждой из указанных групп разработаны методы принятия решений, учитывающие специфику задачи и предпочтения принимающего решения лица.

 

Вопросы для самопроверки:

1.       Что понимается под условиями определенности?

2.       В чем состоит суть подхода к оцениванию систем на основе функции полезности?

3.       Что представляет собой функция полезности?

4.       Что такое прямая функция полезности?

5.       Что такое обратная функция полезности?

6.       Какие шаги нужно выполнить для определения вида функция полезности?

7.       Какие способы определения функции полезности вам известны?

8.       На чем основан способ определения функции полезности с использованием метода экспертных оценок?

9.       На чем основан способ определения функции полезности на основе аппроксимации?

10.  Какие виды аппроксимирующих функций используются на практике чаще всего для аппроксимации функции полезности?

11.  Для каких операций может применяться одноступенчатое представление функции полезности?

12.  Для каких операций могут применяться косинусоидальное и треугольное представления функции полезности?

13.  Какие условия функционирования системназываютусловиями риска?

14.  Какие критерии оценивания эффективности функционирования систем в условиях риска вам известны?

15.  Какой критерий оценивания эффективности функционирования систем в условиях риска используется чаще всего?

16.  Какие условия функционирования системназываютусловиями неопределенности?

17.  Какие критерии оценивания эффективности функционирования систем в условиях неопределенности вам известны?

18.  Чем обусловлен практический выбор того или иного критерия эффективности?

19.  В каком виде обычно формулируется задача оценивания эффективности функционирования систем в условиях неопределенности?

20.  Как формулируется критерий Вальда?

21.  Как формулируется критерий Сэвиджа?

 

Литература по теме:

 

Основная литература:

1.  Волкова В. Н. Теория систем и системный анализ: учебник для академического бакалавриата / В. Н. Волкова, А. А. Денисов. – М.: Юрайт, 2015. – 616с.

2.  Качала В. В. Основы теории систем и системного анализа. Учебное пособие для вузов. – М.: Издательский центр «Академия», 2013 – 272с.

3.  Прокимнов Н.Н. Теория систем и системный анализ. Практикум. – Сайт МФПУ «Синергия».

 

Дополнительная литература:

1.  Анфилатов В. С., Емельянов В. С., Кукушкин А. А. Системный анализ в управлении: учебное пособие / (под ред. Емельянова А.А.) – М.: Финансы и статистика, 2009. – 368с.

2.  Теория систем и системный анализ в управлении организациями: справочник/ ред. В. Н. Волкова и А. А. Емельянов. – М.: Финансы и статистика, 2009. - 848с.

 

Практическое задание:

 

Для заданных значений функции полезности пяти вариантов системы для шести вариантов внешней среды

 

	1	2	3	4	5	6
1	10,4	15,7	10,3	13,1	13,3	14,4
2	17,6	10,4	17,6	15,7	15,7	13,3
3	17,3	17,6	19,2	14,7	15,7	16,9
4	15,7	18,9	17,3	19,3	10,4	11,8
5	12,0	15,7	17,8	18,9	17,6	17,0

 

найти наилучший вариант системы:

1)       по критерию Вальда;

2)       по критерию Сэвиджа.