ворд. Документ Microsoft Word. Литература по теме Тема Основы системного анализа Вопрос Системный подход и системный анализ

• Название: Литература по теме Тема Основы системного анализа Вопрос Системный подход и системный анализ
• Дата: 25.04.2022
• Размер: 0.56 Mb.
• Имя файла: Документ Microsoft Word.docx
• Тип: Литература; #495220
• страница: 5 из 9

Тема 5. Модели формализованного принятия решений

 

Цели изучения темы:

·     изучить модели количественного анализа.

 

Задачи изучения темы:

·     изучить понятия свойства, показателя, критерия;

·     изучить возможные постановки задач количественного анализа;

·     изучить основные подходы к решению задач.

 

Успешно изучив тему, Вы:

Получите представление о:

·     понятии критерия;

·     типах критериев количественного оценивания.

 

Будете знать:

·     что такое множество Парето;

·     что такое скаляризация критерия и способы скаляризации;

·     какие существуют подходы к решению задач векторной оптимизации.

 

Вопросы темы:

1.  Понятие критерия.

2.  Множество Парето.

3.  Векторная оптимизация.

4.  Скаляризация векторного критерия.

 

Вопрос 1. Понятие критерия.

 

Каждое i-ое качество j-ой системы,   может быть описано с помощью некоторой переменной   отображающей определенное свойство системы, значение которой характеризует меру этого качества. Эта мера называется показателем свойства или частным показателем качествасистемы. Каждый показатель y_i может принимать значения из множества (области) допустимых значений  .

Обобщенным показателем качества j-ой системы называется вектор  , компонентами которого являются показатели отдельных системных свойств. Размерность этого вектора определяется числом существенных свойств системы (обратим внимание на то, что обобщенным показателем качества является именно вектор, а не простое множество частных показателей, поскольку между отдельными свойствами могут существовать связи, которые в рамках теории множеств описать весьма сложно).

Частные показатели имеют различную физическую природу и в соответствии с этим различную размерность. Поэтому при переходе к обобщенному показателю качества следует оперировать не с самими показателями, а с их нормированными значениями, обеспечивающими приведение показателей к одному масштабу, что необходимо для их сопоставления.

Задача нормировки решается, как правило, введением относительных безразмерных показателей, представляющих собой отношение измеренного частного показателя к некоторой нормирующей величине, измеряемой в тех же единицах, что и сам показатель

 



 

где

- некоторое «идеальное» значение i-го показателя.

 

Выбор нормирующего делителя для перевода частных показателей в безразмерную форму в значительной мере носит субъективный характер и должен обосновываться в каждом конкретном случае.

Возможны несколько подходов к выбору нормирующего делителя. Укажем следующие.

1)        может задаваться лицом, принимающим решение. Такой способ задания означает, что значение   следует воспринимать как образцовое.

2)       Можно положить  .

3)       В качестве может быть взята разность между максимальным и минимальным допустимыми значениями частного показателя.

 

Требуемое качество системы задается правилами (условиями), которым должны удовлетворять показатели существенных свойств, а проверка их выполнения называется оцениванием качества системы. Таким образом, критерий качества есть показатель существенных свойств системы и правило его оценивания.

Все критерии в общем случае могут принадлежать одному из трех классов.

 

Критерий пригодности.

Согласно этому критерию j-ая система считается пригодной, если значения всех частных показателей  этой системы принадлежат области допустимых значений частных показателей.

 

Критерий оптимальности.

Согласно этому критерию j-ая система считается оптимальной по i-му показателю качества, если все значения частных показателей качества  принадлежат допустимой области и существует хотя бы один частный показатель качества  , по которому достигается оптимум.

 

Критерий превосходства.

Согласно этому критерию j-ая система считается превосходной, если все значения частных показателей качества  принадлежат допустимой области и система оптимальна по всем показателям.

Иллюстрация приведенных формулировок приведена на рис. 11 где по свойствам у_х и у₂ сравниваются характеристики пяти систем 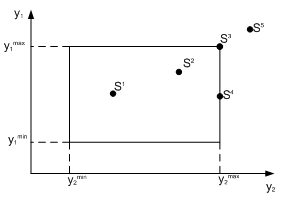 , имеющие допустимые области адекватности значений у₁ и у₂, для которых оптимальные значения определены как   и  соответственно.

 



 

Рис. 11. Примеры критериев оценивания

 

Из рисунка видно, что системы   пригодны по показателям у₁ и у₂. Система S⁵ не является пригодной. Системы  ⁴ оптимальны по показателю у₂. Система S³ является превосходной.

 

Вопрос 2. Множество Парето.

 

Множество Парето определяется как подмножество А* множества альтернатив А. Множество А* (переговорное множество, множество компромиссов) включает альтернативы, которые всегда более предпочтительны по сравнению с любой альтернативой из множества А\А*. При этом любые две альтернативы из множества Парето по предпочтению несравнимы. Альтернативы   и   называются несравнимыми, если альтернатива   превосходит альтернативу   по одним критериям, а альтернатива   превосходит альтернативу   по другим. Выражение   означает, что

 



 

и хотя бы одно из этих неравенств является строгим.

Понятие множества Парето можно пояснить на примере. Пусть имеем задачу оптимизации по двум критериям 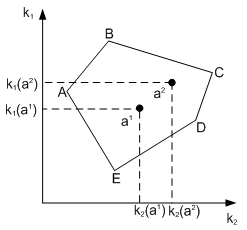 ,  ,где   и   – показатели свойств системы (параметры), значения которых можно выбирать. Целью является выбор оптимальных (в данном случае минимальных) значений параметров. Если изобразить множество критериев в виде многоугольника (рис. 12):

 



 

Рис. 12. Множество Парето

 

и рассмотреть пару точек   и   как показано на рисунке, то легко заметить, что для этих точек справедливо: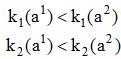

 



 

т.е., точка   является более предпочтительной по отношению к точке  . Поэтому оставлять для рассмотрения точку   не имеет смысла.

Продолжая рассмотрение других точек области многоугольника, придем к тому, что для выбора остаются только точки стороны AE. Для каждой пары этих точек предпочтение по одному показателю сопровождается ухудшением по другому показателю.

Таким образом, нахождение множества Парето может значительно уменьшить затраты на решение задачи выбора за счет сокращения числа подлежащих рассмотрению вариантов.

 

Вопрос 3. Векторная оптимизация.

 

Существует несколько подходов к решению задач многокритериальной оптимизации, которые можно сгруппировать следующим образом:

·     метод выделения главного критерия;

·     метод лексикографической оптимизации;

·     метод последовательных уступок;

·     человеко-машинные процедуры векторной оптимизации.

 

В методе выделения главного критерия лицо, принимающее решение, назначает один главный критерий, остальные выводятся в состав ограничений, т.е., указываются границы, в которых эти критерии могут находиться. Недостатком метода является его вырожденность: нет смысла проводить глубокое системное исследование, если все критерии кроме одного не учитываются.

В методе лексикографической оптимизации предполагается, что критерии, составляющие векторный критерий, могут быть упорядочены на основе отношения абсолютной предпочтительности.

Пусть критерии пронумерованы так, что наиболее важному из них соответствует номер 1. Тогда на первом шаге выбирается подмножество альтернатив  , имеющие наилучшие оценки по первому критерию. Если окажется, что  , то это означает, что есть единственная альтернатива, входящая в  , которая и признается наилучшей. Если  , то на втором шаге выбирается подмножество альтернатив  , имеющих наилучшие оценки по второму критерию, и так далее, до тех пор, пока не будет выявлена лучшая альтернатива. При поиске решения будут учтены, как правило, не все, а лишь наиболее значимые критерии, что не всегда оправдано.

Поэтому в методе последовательных уступок для каждого для каждого из проранжированных критериев назначается допустимое отклонение значение критерия от наилучшего. Затем на первом шаге производится построение подмножества альтернатив  , для которых отклонение оценки по первому критерию от его экстремального значения не превышает допустимого отклонения («уступки»). Далее строится подмножество   на основе второго критерия и его уступки и т.д. При этом уступки назначаются таким образом, чтобы получающееся на каждом шаге подмножество состояло бы как минимум из двух элементов, поскольку одноэлементное или пустое множество приводит к невозможности оптимизации по другим критериям.

Заметим, что если допустимые отклонения для всех компонентов векторного критерия положить равным нулю, то метод последовательных уступок превращается в метод лексикографической оптимизации.

Достоинством человеко-машинные процедуры векторной оптимизации является сочетание возможностей ЭВМ по быстрому проведению больших расчетов и способностей человека к восприятию альтернатив в целом, без длительного изучения и сравнения по отдельным критериям. Общая схема этих методов состоит в следующем.

Тем или иным способом лицо, принимающее решение, указывает свои предпочтения на множестве векторных оценок альтернатив. На основе полученной информации ЭВМ автоматически сужает исходное множество альтернатив, сообщая по окончанию процесса сужения наилучшие альтернативы. Затем лицо, принимающее решение, указывает допустимые уровни снижения оценок по одним критериям, требуемые более высокие уровни оценок по другим критериям, и ЭВМ вновь выполняет необходимые расчеты.

Итеративный процесс продолжается до тех пор, пока не будет решена задача выбора альтернатив. В процессе решения поиск ведется среди элементов множества Парето.

 

Вопрос 4. Скаляризация векторного критерия.

 

В этих методах многокритериальная задача заменяется однокритериальной. Методы, основанные на свертке векторного критерия в скалярный, предполагают переход к решению задачи

 



 

где

- скалярный критерий, представляющий собой некоторую функцию от значений компонентов векторного критерия:

 



 

Основной проблемой этого подхода является построение функции f, называемой сверткой.

Решение задачи требует выполнения следующих этапов.

Обоснование допустимости свертки.Требует подтверждения, что рассматриваемые показатели эффективности являются однородными. Известно, что показатели эффективности разделяются на три группы: показатели результативности, ресурсоемкости и оперативности. В общем случае разрешается свертка показателей, входящих в обобщенный показатель для каждой группы отдельно. Свертка показателей разных групп может привести к потере физического смысла такого критерия.

Нормализация критериев. Проводится аналогично нормировке показателей.

Учет приоритетов критериев. Осуществляется в большинстве методов свертывания путем задания вектора коэффициентов важности критериев l: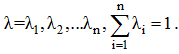

 



 

где

 – коэффициент важности критерия  , обычно совпадающий с коэффициентом значимости частного показателя качества.

 

Определение коэффициентов важности критериев, как и в случае с показателями, сталкивается с серьезными трудностями и сводится либо к использованию формальных процедур, либо к применению экспертных оценок.

В результате нормализации и учета приоритетов критериев вместо исходной векторной оценки   альтернативы   образуется новая векторная оценка

 



 

где

 - нормированный критерий, он находится аналогично нормированному показателю. Именно эта полученная векторная оценка подлежит преобразованию с использованием функции свертки.

 

Свертка показателей. Способ свертки зависит от характера показателей и целей оценивания систем. Известны несколько видов свертки. Наиболее часто использую аддитивная и мультипликативная свертки компонентов векторного критерия.

Аддитивная свертка компонентов векторного критериясостоит в представлении обобщенного скалярного критерия в виде суммы взвешенных нормированных частных критериев: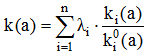

 



 

Такие критерии образуют группу аддитивных критериев, их свертка основана на использовании принципа справедливой компенсации абсолютных значений нормированных частных критериев. Сутью этого принципа является утверждение: справедливым следует считать такой компромисс, при котором суммарныйуровень абсолютного снижения значений одного или нескольких показателей не превышает суммарного уровня абсолютного увеличения значений других показателей. Главный недостаток аддитивных критериев состоит в том, что они не вытекают из объективной роли частных критериев в определении качества системы и поэтому выступают как формальный математический прием, придающий задаче удобный вид.Кроме того, низкие оценки по одним критериям могут компенсироваться высокими оценками по другим критериям. Это значит, что уменьшение одного из критериев вплоть до нулевого значения может возмещаться возрастанием другого.

Мультипликативная сверткакритерия состоит в представлении обобщенного скалярного критерия в виде произведения: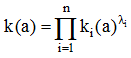

 



 

Значение критерия получается путем перемножения частных критериев   возведенных в степени  . Если все частные критерии имеют одинаковую важность, то  =1. При разной важности критериев  ≠1.

В мультипликативных критериях компромисс достигается по отношению не к абсолютным, а к относительным изменениям частных критериев, а именно, суммарный уровень относительного снижения значений одного или нескольких критериев не превышает суммарного уровня относительного увеличения значений других критериев.

Достоинством мультипликативного критерия является то, что при его использовании не требуется нормировки частных критериев. К его недостаткам относится то, что он компенсирует недостаточную величину одного частного критерия избыточной величиной другого и имеет тенденцию сглаживать уровни частных критериев за счет неравнозначных первоначальных значений частных критериев.

Выбор между аддитивной и мультипликативной свертками частных критериев определяется степенью важности абсолютных или относительных изменений значений частных критериев соответственно.

 

Выводы:

1.  В случае, когда относительно изучаемой системы доступны сведения в виде значений ее количественных показателей, становится возможным проведения оценивания и принятия решений на основе формальной математической модели. Необходимым элементом этой модели является критерий качества анализируемой системы.

2.  Критерии разделяются на частные и обобщенные. Обобщенный критерий представляет собой вектор, компонентами которого являются показатели отдельных системных свойств.

3.  В целях достижения возможности сравнения разнородных показателей и приведение их к единому диапазону значений показатели нормируются. Для выполнения операции нормирования применяется один из нескольких типовых приемов.

4.  Критерии сравнения образуют три основные группы. Применение того или критерия определяется существом решаемой задачи. Критерий превосходства положен в основу нахождения множества Парето, нахождение которого позволяет значительно упростить решение задачи оценивания и выбора.

5.  Решать задачу многокритериальной оптимизации можно с применением одного из группы методов векторной оптимизации. Использование методов этой группы основано на пошаговой процедуре, на каждом шаге которой производится последовательное сужение исходного множества.

6.  Методы, основанные на свертке векторного критерия в скалярный, предполагают переход к решению однокритериальной задачи оптимизации. Переход производится на основе применения одного из известных методов свертки, выбор которого определяется существом решаемой задачи и предпочтениями аналитика.

 

Вопросы для самопроверки:

1.       Что называется частным показателем качествасистемы?

2.       Что называется обобщеннымпоказателем качествасистемы?

3.       Что такое нормированный показатель?

4.       В чем необходимость проведения нормирования показателей?

5.       Какие применяются способы нормирования показателей?

6.       Какие классы критериев оценивания систем вам известны?

7.       Как определяется критерий пригодности?

8.       Как определяется оптимальности?

9.       Как определяется превосходства?

10.  Как определяется множество Парето?

11.  Какие существуют подходы к решению задач многокритериальной оптимизации?

12.  В чем состоит суть метода выделения главного критерия?

13.  В чем состоит суть метода лексикографической оптимизации?

14.  В чем состоит суть метода последовательных уступок?

15.  Какая цель преследуется методами скаляризации векторного критерия?

16.  Что понимается под сверткой показателей?

17.  Какие шаги выполняются при осуществлении свертки?

18.  Какие способы свертки вам известны?

19.  В чем состоят достоинства и недостатки аддитивной свертки?

20.  В чем состоят достоинства и недостатки мультипликативной свертки?

 

Литература по теме:

 

Основная литература:

1.  Волкова В. Н. Теория систем и системный анализ: учебник для академического бакалавриата / В. Н. Волкова, А. А. Денисов. – М.: Юрайт, 2015. – 616с.

2.  Качала В. В. Основы теории систем и системного анализа. Учебное пособие для вузов. – М.: Издательский центр «Академия», 2013 – 272с.

3.  Прокимнов Н.Н. Теория систем и системный анализ. Практикум. – Сайт МФПУ «Синергия».

 

Дополнительная литература:

1.  Анфилатов В. С., Емельянов В. С., Кукушкин А. А. Системный анализ в управлении: учебное пособие / (под ред. Емельянова А.А.) – М.: Финансы и статистика, 2009. – 368с.

2.  Теория систем и системный анализ в управлении организациями: справочник/ ред. В. Н. Волкова и А. А. Емельянов. – М.: Финансы и статистика, 2009. – 848с.

3.  Орлов А.И. Теория принятия решений. Учебное пособие. — М.: Издательство «Март», 2004. - 656 с.