ВНЕАУДИТ САМОСТОЯТ.РАБОТА. Методические рекомендации по выполнению внеаудиторной самостоятельной работы обучающихся по учебной дисциплине
 Скачать 0.62 Mb. Скачать 0.62 Mb.
|
|
ВСР№9 «Элементарные функции. Сложные функции». Цель: Знать определение функции, элементарной функции, сложной функции. Форма самостоятельной деятельности: составление конспекта Методические рекомендации Найти в Интернете или учебной литературе материал и изучив тему, письменно ответьте на вопросы: 10. Сформулируйте определение функции. 20. Какую функцию называют сложной? 30. Перечислите основные элементарные функции (свойства + график). 40. Какие функции называются элементарными? ВСР№12. «Обратные функции». Цель: Развитие интереса к предмету. Форма самостоятельной деятельности: построить графики обратных функций и провести их сравнительный анализ Методические рекомендации
1. Алимов Ш.А. и др. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углубленный уровни).10—11 классы. — М., 2014. 2. Гусев В.А., Григорьев С.Г., Иволгина С.В. Математика для профессий и специальностей социально-экономического профиля: учебник для студ. учреждений сред. проф. образования. — М., 2014. Полезные Интернет – сайты:
ВСР№11. «Показательные и логарифмические функции: их свойства и графики» Цель: Развитие интереса к предмету. Форма самостоятельной деятельности: исследовать функции и построить их графики. Задания:
Методические рекомендации
1. Алимов Ш.А. и др. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углубленный уровни).10—11 классы. — М., 2014. 2. Гусев В.А., Григорьев С.Г., Иволгина С.В. Математика для профессий и специальностей социально-экономического профиля: учебник для студ. учреждений сред. проф. образования. — М., 2014. Полезные Интернет – сайты:
ВСР№12. «Производная». Цель: Развитие интереса к предмету. Форма самостоятельной деятельности: подготовка исторических справок Подготовить исторические справки: 1) Происхождение понятия производной. 2) Символы и термины производной. Методические рекомендации
ВСР№13. «Производная и ее применение». Цель: Развитие интереса к предмету. Форма самостоятельной деятельности: заполнить таблицу «Межпредметные связи темы «Производная». Методические рекомендации
1. Алимов Ш.А. и др. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углубленный уровни).10—11 классы. — М., 2014. 2. Гусев В.А., Григорьев С.Г., Иволгина С.В. Математика для профессий и специальностей социально-экономического профиля: учебник для студ. учреждений сред. проф. образования. — М., 2014. Полезные Интернет – сайты:
ВСР№14 «Решение прикладных задач». Цель: Уметь применять определение производной и ее механический смысл к решению прикладных задач. Форма самостоятельной деятельности:Выполнение заданий Методические рекомендации Физический смысл первой производной. Физический смысл производной заключается в том, что мгновенная скорость движения 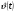 в момент времени t есть производная пути по времени, т.е. в момент времени t есть производная пути по времени, т.е.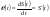 Физический смысл второй производной. Ускорение прямолинейного движения в данный момент времени есть первая производная скорости по времени или вторая производная пути по времени. 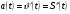 Пример. 1. Зависимость пути от времени при прямолинейном движении точки задана уравнением 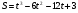 . .В какой момент времени ускорение движения точки будет равно 24 м/с2? Решение. а) Найдем скорость движения точки по формуле: 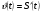 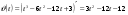 б) Найти ускорение движения точки по формуле: 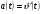 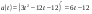 в) Из условия 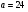 м/с2, найти момент времени: м/с2, найти момент времени: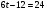 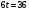 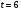 c cОтвет: 6 с.
Правила.
Производные основных элементарных функций.
Используя методические рекомендации, выполните задания:
ВСР№15.«Вычисление площадей плоских фигур с помощью определённого интеграла». Цель: Развитие интереса к предмету. Форма самостоятельной деятельности:
Методические рекомендации
Инструкция по созданию кроссвордов. 1) Начало начал составления кроссворда. Оптимальный вариант – это выбрать сетку и начать ее заполнять. При обретении достаточного опыта, можно пойти и от обратного: то есть, сетку строить потом, но это достаточно сложно – нужно симметрично располагать слова и т.д. Поэтому начнем с простого: сначала – сетка. Если сложно нарисовать ее самостоятельно, то легко можно взять сетку из любого печатного издания – конечно, если это не какой-нибудь мудреный эксклюзив, а наша стандартная классическая черно-белая сетка разных конфигураций. 2) Обратите внимание на количество пересечений. Самое простое – это когда слова пересекаются в двух, максимум – в трех местах. Больше – это будет намного сложнее, особенно к концу кроссворда. Допустим, сетка с двойным-тройным пересечением слов выбрана, и теперь переходим к ее заполнению. 3) Старайтесь, чтобы в местах пересечений оказались гласные. Составить пересекающееся слово в варианте «-а-и-а» гораздо легче, чем «-к-с-н». Если все же в пересечении попали согласные, то желательно выбирать легко сочетаемые и часто встречающиеся, например, «к», «р», «с». В предпоследнее пересечение можно поставить «н» или «к», потому что в русском языке очень много слов, оканчивающихся на «-на», или «-ка». Если же пересечение не в предпоследней букве, а, например, в третьей с конца, то тоже ничего страшного: сколько можно вспомнить слов, оканчивающихся на «-сть», «ист», «лог», интересных фамилий или географических названий. Однако шипящие и буквы «э», «ю», «я», а также мягкие-твердые знаки в клетках пересечения – это лишняя головная боль. 4) Придумайте сначала длинные слова, состыкуйте их друг с другом, а уж затем подгоняйте под них короткие. Выбор оригинальных слов из трех букв довольно невелик, и поэтому они, по техническим причинам, кочуют из одного кроссворда в другой. Наиболее интересные слова лучше заполнять сначала – потом, к концу сетки, придется элементарно подгонять их по уже имеющемуся в наличии сочетанию букв, а в начале пути еще есть полный простор. 5) Не мудрите! Примитивность и доступность – это разные вещи! 4. Не забудьте указать ответы. 5. Рекомендуемая литература: 1. Алимов Ш.А. и др. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углубленный уровни).10—11 классы. — М., 2014. 2. Гусев В.А., Григорьев С.Г., Иволгина С.В. Математика для профессий и специальностей социально-экономического профиля: учебник для студ. учреждений сред. проф. образования. — М., 2014. | ||||||||||||||||||||||||||||||||||||||||||||||||||||

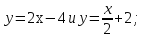
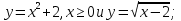
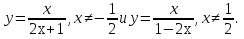
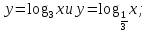
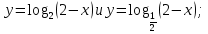
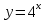 и
и 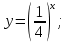
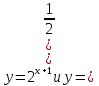 .
.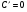
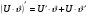
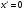
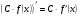
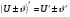
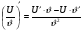
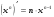 ,
, 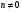
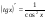
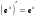
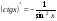
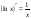
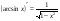
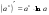
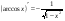
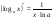
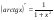
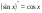
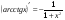
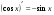
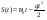 с начальной скоростью
с начальной скоростью 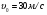 ,
, 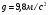 . Через сколько секунд скорость станет равной
. Через сколько секунд скорость станет равной 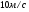 ?
?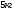 , движущееся по закону
, движущееся по закону 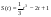 в момент времени
в момент времени 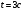 .
.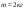 , движущейся по закону
, движущейся по закону 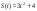 в момент времени
в момент времени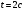
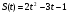 . Найти ускорение точки в момент времени
. Найти ускорение точки в момент времени 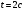 .
.