ргз по сопромату. Методические указания для выполнения расчетного задания
 Скачать 1.5 Mb.
|
|
Выполните задания (образец выполнения см. в конце). Обязательно напишите все выводы и постройте графики (полученные прямые не должны совпадать, правильно выбирайте масштаб). Можно для расчетов использовать Exel. Вариант - номер по списку в журнале. Срок сдачи до 15 мая. Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Санкт-Петербургский горный университет» Кафедра высшей математики МАТЕМАТИКА ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ. КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ. Методические указания для выполнения расчетного задания САНКТ-ПЕТЕРБУРГ 2018 УДК 519.2.06(073) МАТЕМАТИКА. Элементы математической статистики. Корреляционно-регрессионный анализ: Методические указания для выполнения расчетного задания / Санкт-Петербургский горный университет. Сост.: Л.В.Бакеева, Е.В. Пастухова, СПб, 2018. 42 с. Методические указания разработаны в соответствии с требованиями государственного образовательного стандарта высшего образования. Методические указания содержат основные понятия математической статистики, в нем излагаются основы выборочного метода и корреляционно-регрессионного анализа. Изложение теоретического материала сопровождается разобранными типовыми примерами. Включены задания для самостоятельной работы. Методические указания могут быть использованы для работы на практических занятиях и для выполнения заданий самостоятельной работы обучающимися, изучающими элементы математической статистики в рамках учебной дисциплины «Математика», в соответствии с программами подготовки специалистов и бакалавров инженерно-технических и экономических направлений подготовки и специальностей Научный редактор проф. А.П. Господариков
1. Выборки и их характеристики 1.1 Предмет математической статистики Математическая статистика – раздел математики, в котором изучаются методы сбора, систематизации и обработки результатов наблюдений массовых случайных явлений для выявления существующих закономерностей. Математическая статистика тесно связана с теорией вероятностей. Обе эти математические дисциплины изучают массовые случайные явления. При этом теория вероятностей выводит из математической модели свойства реального процесса, а математическая статистика устанавливает свойства математической модели, исходя из данных наблюдений (говорят «из статистических данных»). Предметом математической статистики является изучение случайных величин (или случайных событий, процессов) по результатам наблюдений. Полученные в результате наблюдения (опыта, эксперимента) данные сначала надо каким-либо образом обработать: упорядочить, представить в удобном для обозрения и анализа виде. Это первая задача. Затем, это уже вторая задача, оценить, хотя бы приблизительно, интересующие нас характеристики наблюдаемой случайной величины. Например, дать оценку неизвестной вероятности события, оценку неизвестной функции распределения, оценку математического ожидания, оценку дисперсии случайной величины, оценку параметров распределения, вид которого неизвестен, и т.д. Следующей, назовем ее условно третьей, задачей является проверка статистических гипотез, т.е. решение вопроса согласования результатов оценивания с опытными данными. Например, выдвигается гипотеза, что: а) наблюдаемая случайная величина подчиняется нормальному закону; б) математическое ожидание наблюдаемой случайной величины равно нулю; в) случайное событие обладает данной вероятностью и т.д. Одной из важнейших задач математической статистики является разработка методов, позволяющих по результатам обследования выборки (т.е. части исследуемой совокупности объектов) делать обоснованные выводы о распределении признака (случайной величины  ) изучаемых объектов по всей совокупности.Результаты исследования статистических данных методами математической статистики используются для принятия решения в задачах планирования, управления, прогнозирования и организации производства, при контроле качества продукции, при выборе оптимального времени настройки и замены действующей аппаратуры и т.д., то есть для научных и практических выводов. Говорят, что «математическая статистика – это теория принятия решений в условиях неопределенности». 1.2 Генеральная и выборочная совокупности Пусть требуется изучить данную совокупность объектов относительно некоторого признака. Например, рассматривая работу диспетчера, можно исследовать: его загруженность, тип клиентов, скорость обслуживания, моменты поступления заявок и т.д. Каждый такой признак (и их комбинации) образует случайную величину, наблюдения над которой мы и производим. Совокупность всех подлежащих изучению объектов или возможных результатов всех мыслимых наблюдений, производимых в неизменных условиях над одним объектом, называется генеральной совокупностью. Определение. Генеральная совокупность – это случайная величина  , заданная на пространстве элементарных событий  с выделенным в ней классом  подмножеств событий, для которых указаны их вероятности.Зачастую проводить сплошное обследование, когда изучаются все объекты, например – перепись населения, трудно или дорого, экономически нецелесообразно, а иногда невозможно. В этих случаях наилучшим способом обследования является выборочное наблюдение: выбирают из генеральной совокупности часть ее объектов («выборку») и подвергают их изучению. Выборочной совокупностью (выборкой) называется совокупность объектов, отобранных случайным образом из генеральной совокупности. Определение. Выборка – это последовательность  независимых одинаково распределенных случайных величин, распределение каждой из которых совпадает с распределением генеральной случайной величины.Число объектов (наблюдений) в совокупности, генеральной или выборочной, называется ее объемом; обозначается соответственно через  или  . Конкретные значения выборки, полученные в результате наблюдений (испытаний), называют реализацией выборки и обозначают строчными буквами  .Метод статистического исследования, состоящий в том, что на основе изучения выборочной совокупности делается заключение о всей генеральной совокупности, называется выборочным. Для получения хороших оценок характеристик генеральной совокупности необходимо, чтобы выборка была репрезентативной (или представительной), то есть достаточно полно представлять изучаемые признаки генеральной совокупности. Условием обеспечения репрезентативности выборки, является согласно закону больших чисел, соблюдение случайности отбора, то есть все объекты генеральной совокупности должны иметь равные вероятности попасть в выборку. Различают выборки с возвращением (повторные) и без возвращения (бесповторные). В первом случае отобранный объект возвращается в генеральную совокупность перед извлечением следующего; во втором - не возвращается. Заметим, что если объем выборки значительно меньше объема генеральной совокупности, различие между повторной бесповторной выборками очень мало, его можно не учитывать. В зависимости от конкретных условий для обеспечения репрезентативности применяют различные способы отбора: простой, при котором из генеральной совокупности извлекают по одному объекту; типический, при котором генеральную совокупность делят на «типические» части и отбор осуществляется из каждой части; механический, при котором отбор производится через определенный интервал; серийный, при котором объекты из генеральной совокупности отбираются «сериями», которые должны исследоваться при помощи сплошного обследования. На практике обычно пользуются сочетанием вышеупомянутых способов отбора. 1.3 Статистическое распределение выборки Пример 1. Десять абитуриентов проходят тестирование по математике. Каждый из них может набрать от 0 до 5 баллов включительно. Пусть  - количество баллов, набранных  м ( ) абитуриентом. Тогда значения  – все возможные количества баллов, набранных одним абитуриентом, – образуют генеральную совокупность. Выборка  – результат тестирования 10 абитуриентов. Реализациями выборки могут быть следующие наборы чисел:  или  , то есть все возможные комбинации десяти чисел от 0 до 5.Пусть изучается некоторая случайная величина  . С этой целью над случайной величиной производится ряд независимых опытов (наблюдений). В каждом из этих опытов величина принимает то или иное значение.Пусть она приняла  раз значение  ,  раз – значение  ,…,  раз - значение  . При этом  - объем выборки. Значения , ,…, называются вариантами случайной величины , а изменение этих значений варьированием. Расположение выборочных наблюдаемых значений случайной величины (признака) в порядке неубывания называется ранжированием статистических данных. Полученная таким образом последовательность  ,  ,…, значений случайной величины (где  … и  ,…,  ) называется вариационным рядом.Числа  , показывающие сколько раз встречаются варианты  в ряде наблюдений, называются частотами, а отношение их к объему выборки – частостями или относительными частостями (обозначают  или  ), то есть  , где  .Перечень вариантов и соответствующих им частот или частостей называется статистическим распределением ряда или статистическим рядом. Различают дискретные и непрерывные статистические ряды. Дискретным статистическим рядом называется ранжированная совокупность вариант  с соответствующими им частотами. Записывается дискретный ряд в виде таблицы. Первая строка содержит варианты, а вторая их частоты или частости.Пример 2. В результате тестирования (см. пример 1) группа абитуриентов набрала баллы: 5, 3, 0, 1, 4, 2, 5, 4, 1, 5. Записать полученную выборку в виде статистического ряда. Решение. Случайная величина – число набранных баллов является дискретной случайной величиной.Вначале составим ранжированный вариационный ряд ,  ,…,  , то есть расположим числа (баллы) в порядке неубывания их величин:0, 1, 1, 2, 3, 4, 4, 5, 5, 5. Подсчитав частоту и частость вариантов  ,  ,  ,  ,  ,  получим статистическое распределение выборки (так называемый дискретный статистический ряд):
или
В случае, когда число значений признака (случайной величины ) велико или признак является непрерывным (то есть когда случайная величина может принять любое значение в некотором интервале), составляют интервальный статистический ряд. В первую строку таблицы статистического распределения вписывают частичные промежутки  ,  ,…,  , которые берут обычно одинаковыми по длине. Для определения величины интервала  можно использовать формулу Стерджесса: ,где  – размах признака, то есть разность между наибольшим и наименьшим значениями признака,  – число интервалов. За начало первого интервала рекомендуется брать величину  . Во второй строчке статистического ряда вписывают количество наблюдений  , попавших в каждый интервал.Пример 3. Измерили рост (с точностью до 1 см) 30 наудачу отобранных студентов. Результаты измерений таковы: 178, 160, 154, 183, 155, 153, 167, 186, 163, 155, 157, 175, 170, 160, 159, 173, 182, 167, 171, 169, 179, 165, 156, 179, 158, 171, 175, 173, 164, 172. Построить интервальный статистический ряд. Решение. Для удобства проранжируем полученные данные: 153, 154, 155, 155, 156, 157, 158, 159, 160, 163, 164, 165, 166, 167, 167, 169, 170, 171, 171, 172, 173, 173, 175, 175, 178, 179, 179, 182, 183, 186. Очевидно, что рост студентов – непрерывная случайная величина. Для полученной выборки:   ,  . По формуле Стерджесса, при  , находим длину частичного интервала: .Примем  . Тогда  . Число интервалов:  .Исходные данные разбиваем на 6 интервалов:  ,  ,  ,  ,  ,  .Подсчитав число студентов ( ), попавших в каждый из полученных промежутков получим интервальный статистический ряд:
1.4 Эмпирическая функция распределения Эмпирической (статистической) функцией распределения называется функция  , определяющая для каждого значения  относительную частоту события  . Следовательно, по определению: .Для нахождения эмпирической функции распределения удобно  записать в виде: ,где  объем выборки,  число выборочных значений величины , меньших .Эмпирическую функцию распределения можно задать таблично или графически. Пример 4. Построить функцию , используя условия и результаты примера 2.Решение. Объем выборки по условию примера  . Наименьшая варианта равна 0, значит  при  (наблюдений меньше 0 нет). Тогда  . Если  , то неравенство  выполняется для варианты , которая встречается 1 раз ( ), поэтому  и т.д. Окончательно получаем: График эмпирической функции распределения приведен на рисунке 1. Р  ис. 1. Эмпирическая функция распределения дискретной случайной величины В данном примере функция есть выборочная функция распределения дискретной случайной величины и построена она по дискретному статистическому ряду.Если случайная величина непрерывная и ее выборочные значения представлены в виде интервального статистического ряда, то выборочную функцию распределения строят иначе. Рассмотрим построение эмпирической функции распределения для интервального статистического ряда на примере. Пример 5. Построить функцию , используя условия и результаты примера 3.Решение. Очевидно, что для   , так как  .Используя результаты расчетов, представленных в таблице, подсчитаем на концах интервалов значения функции  в виде «наращенной относительной частоты»:
Табличные значения не полностью определяют выборочную функцию распределения непрерывной случайной величины, поэтому при графическом изображении такой функции ее доопределяют, соединив точки графика, соответствующие концам интервала, отрезками прямой (рисунок 2):  1.5 Графическое изображение статистического распределения Статистическое распределение изображается графически (для наглядности) в виде так называемых полигона и гистограммы. Полигон, как правило, служит для изображения дискретного статистического ряда (т.е. варианты отличаются на постоянную величину). Полигоном частот называют ломаную, отрезки которой соединяют на плоскости точки с координатами  ,  ,…,  ; полигоном частостей – ломаную, соединяющую точки с координатами  ,  ,…,  . Иногда полигон называют многоугольником распределения.Варианты откладываются на оси абсцисс, а частоты и соответственно частости – на оси ординат.Пример 6. Пусть дана выборка в виде распределения частот:
Построить полигон частостей. Решение. Статистический вариационный ряд можно записать в виде (см. пример 2):
Полигон частостей для данного ряда имеет вид, изображенный на рисунке 3: 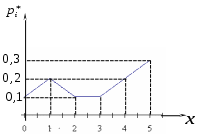 Рис.3. Полигон частостей Полигон частостей является статистическим аналогом многоугольника распределения дискретной случайной величины. Для непрерывно распределенного признака (то есть варианты могут отличаться одна от другой на сколь угодно малую величину) можно построить полигон частот, взяв середины интервалов в качестве значений признака  . Однако чаще распределение непрерывного признака изображают графически в виде так называемой гистограммы.Гистограммой частот (частостей) называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины , а высоты равны частотам или частостям соответствующих интервалов. Если соединить середины верхних оснований прямоугольников отрезками прямой, то можно получить полигон того же распределения.Пример 7. Построить гистограмму частостей по данным группировки промышленных предприятий по средней годовой стоимости основных производственных фондов, приведенным в таблице.
Решение. Для построения гистограммы частостей, найдем  . Так как объем выборки  , то  ;  ;  ;  ;  . Гистограмма частостей изображена на рисунке 4: |
.
.
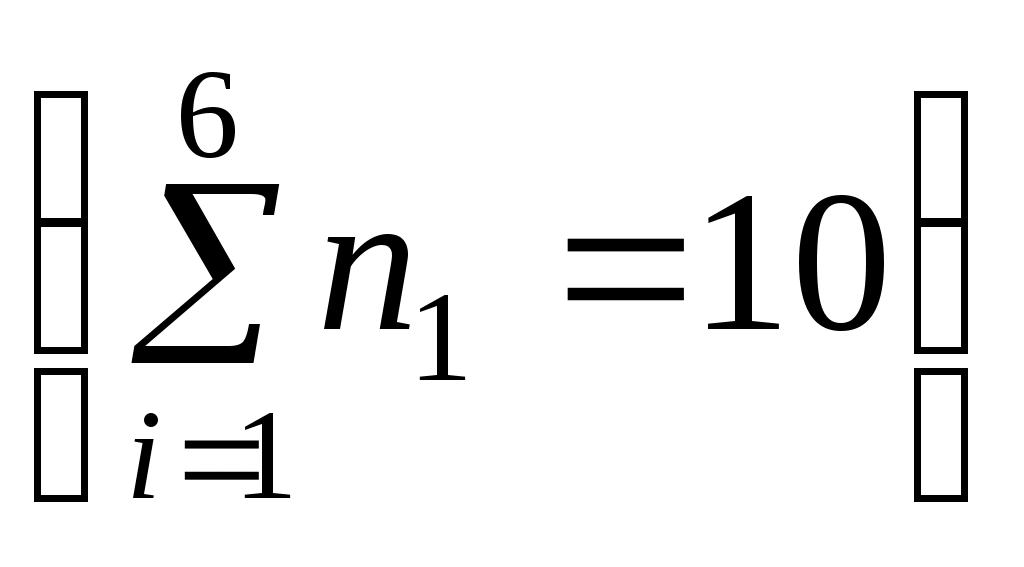
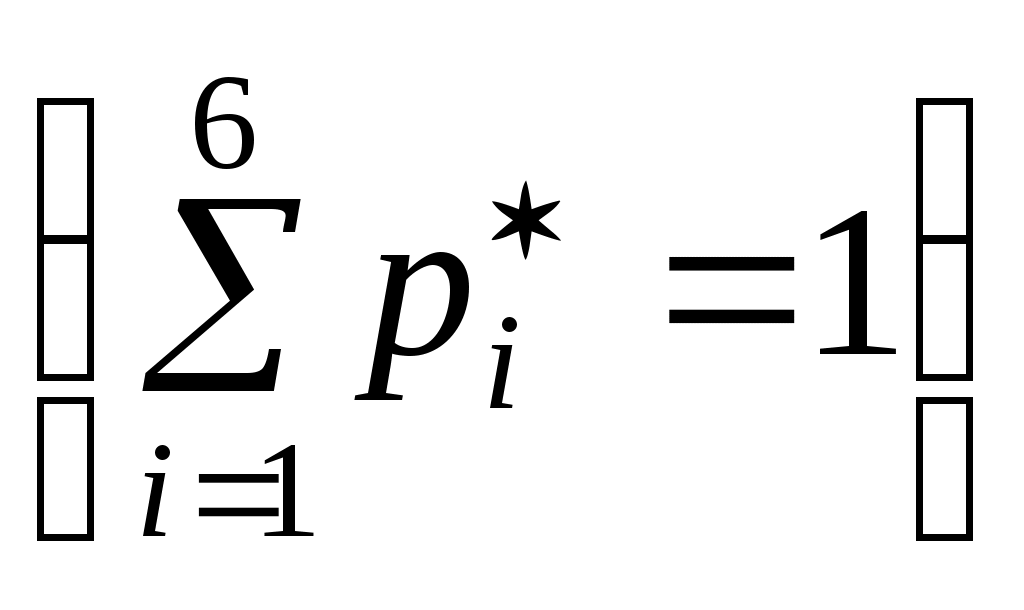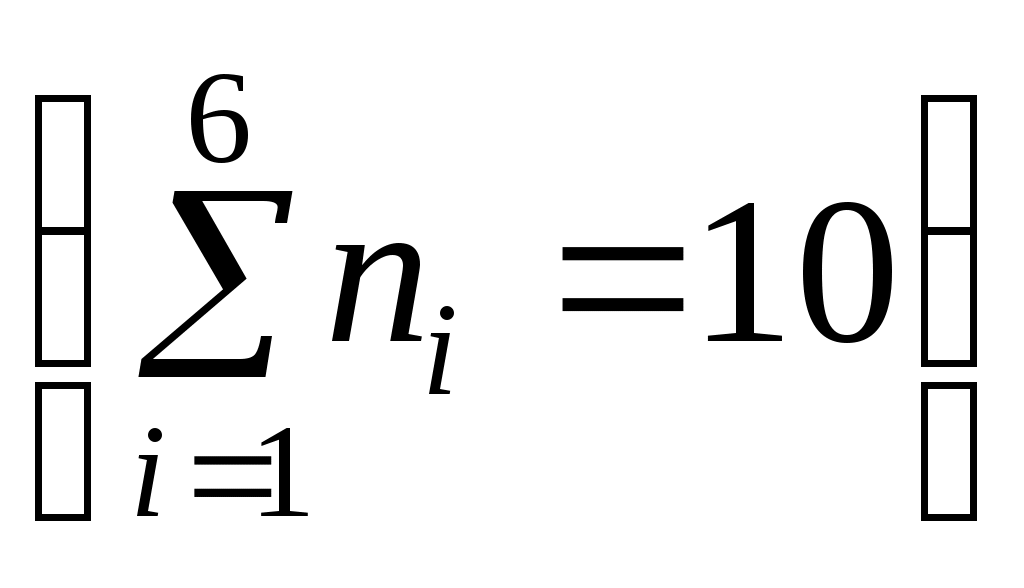
