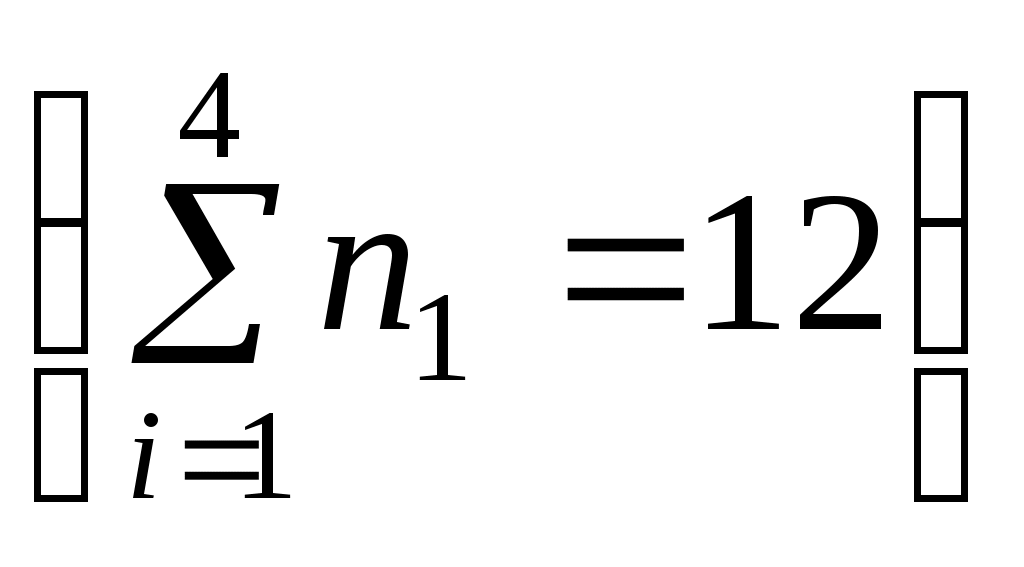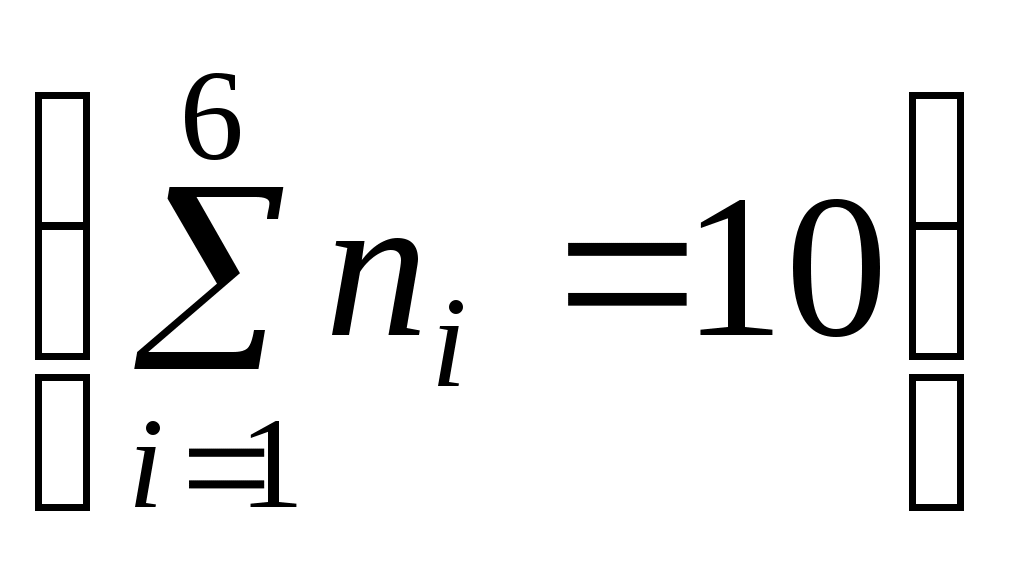Найти выборочную среднюю и выборочную дисперсию.
Решение. Построим сначала статистический ряд распределения:
Выручка, 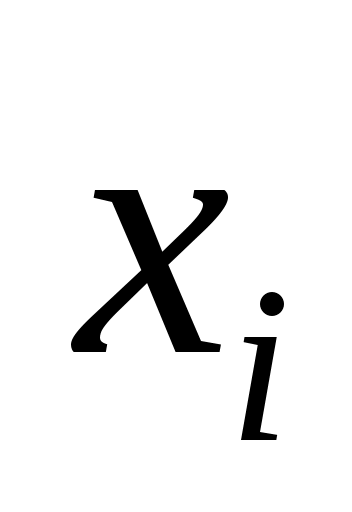
|
2,2
|
2,3
|
2,4
|
2,5
|
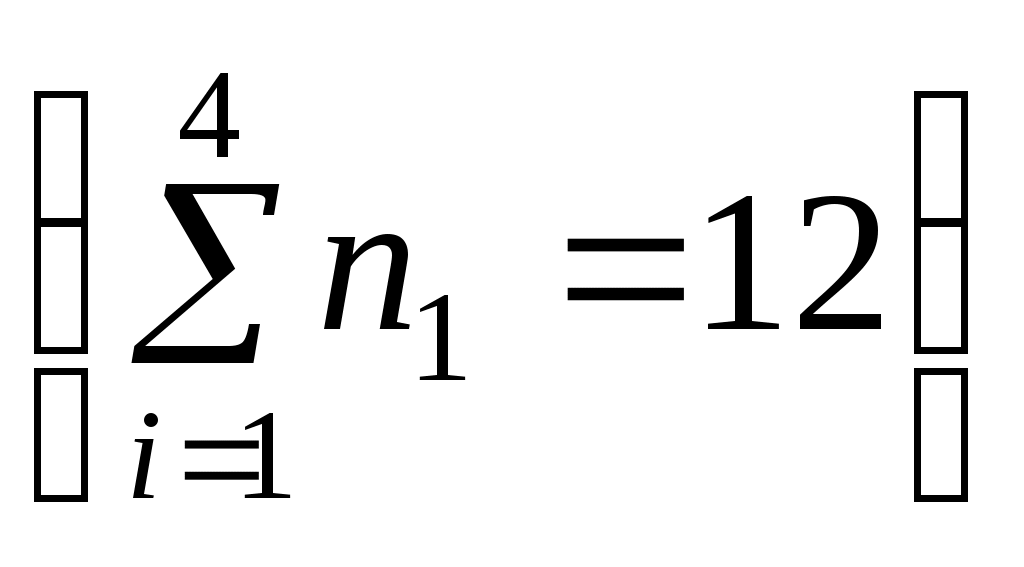
|
Частота, 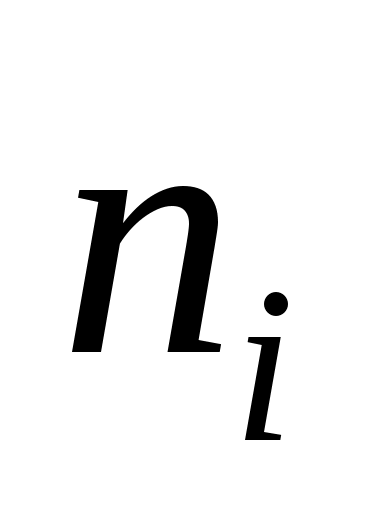
|
5
|
3
|
2
|
2
|
Найдем выборочную среднюю:
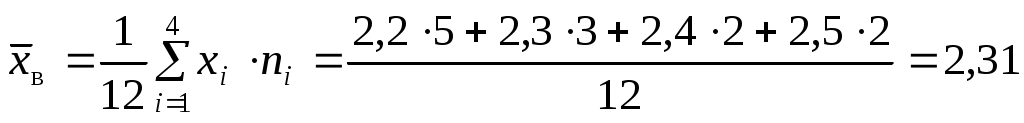 . .
Для вычисления выборочной дисперсии используем формулу 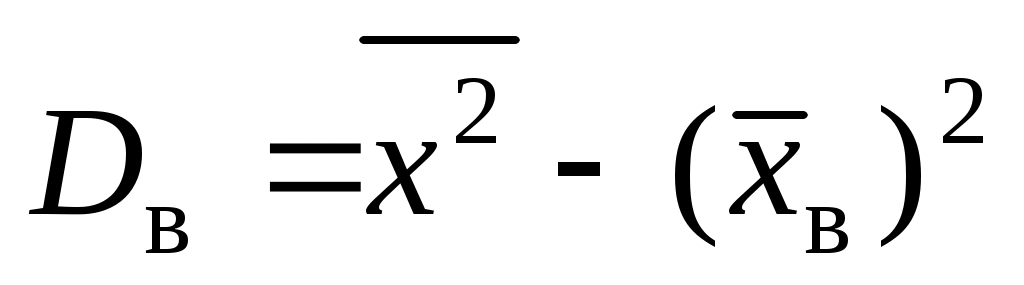 . Чтобы воспользоваться данной формулой найдем сначала . Чтобы воспользоваться данной формулой найдем сначала 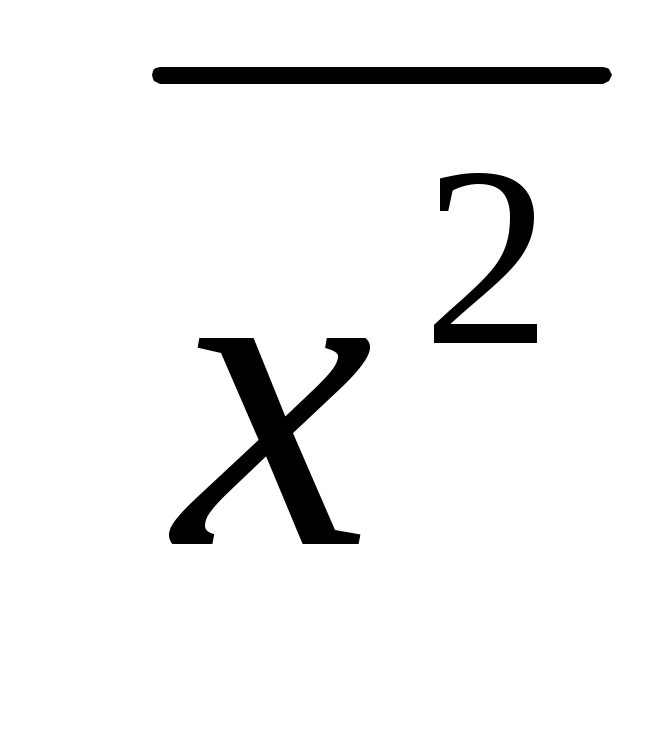 : :
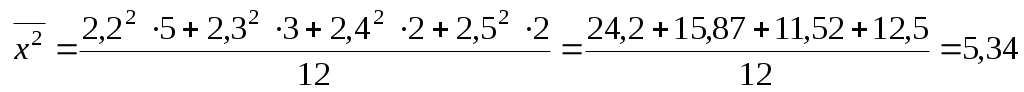 тогда тогда 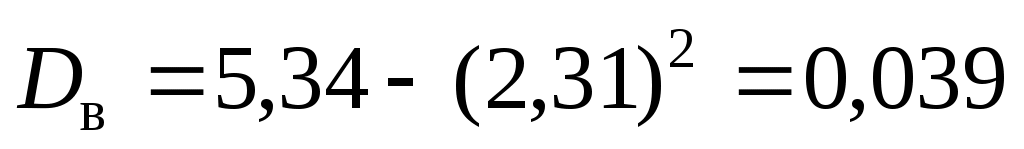 . .
В качестве описательных характеристик вариационного ряда 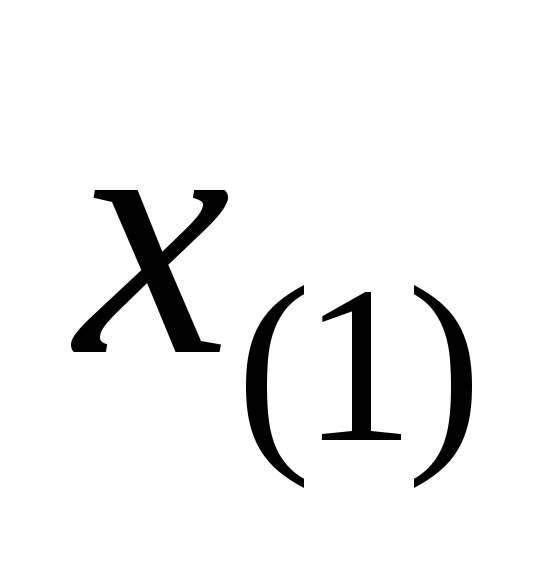 , ,  ,…, ,…, 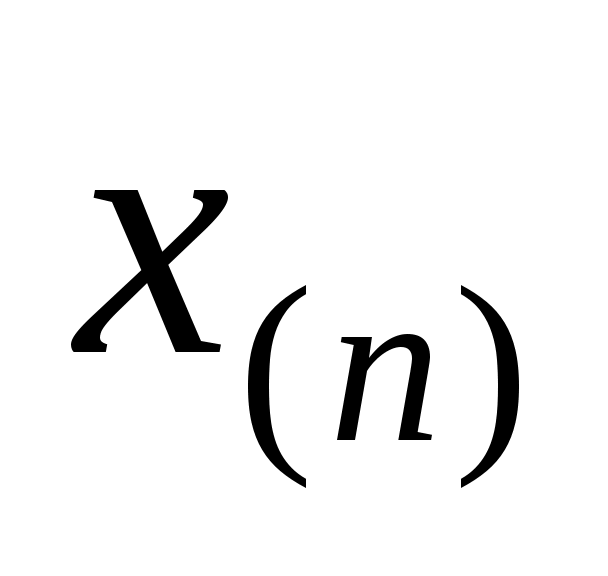 (или полученного из него статистического распределения выборки) используется медиана, мода, размах вариации (выборки). (или полученного из него статистического распределения выборки) используется медиана, мода, размах вариации (выборки).
Размахом вариации называется число:
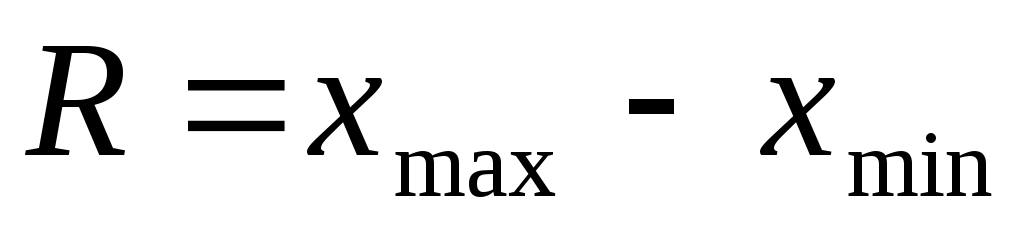 , ,
где 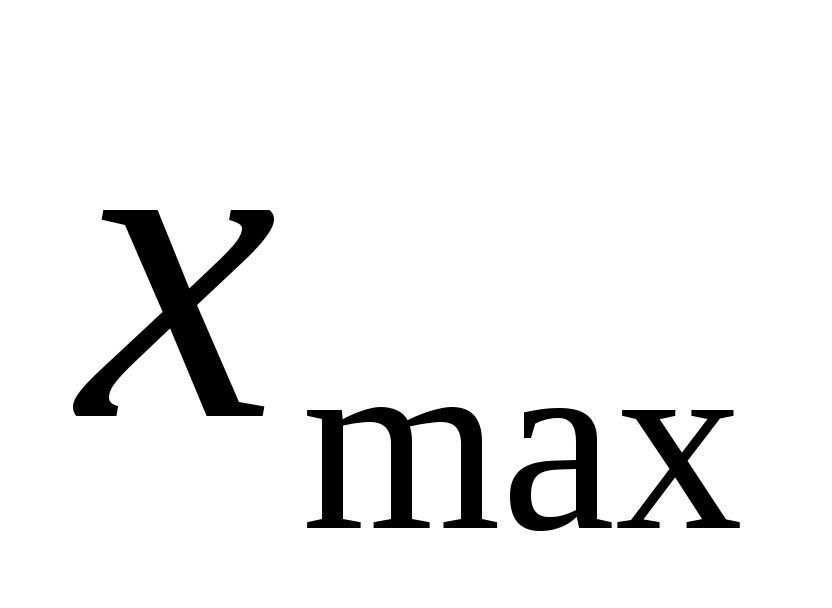 - наибольшая, - наибольшая, 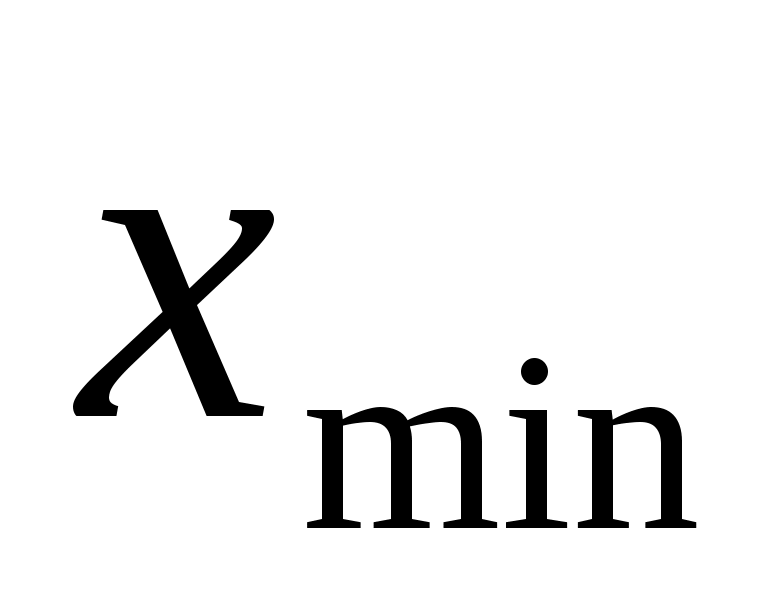 - наименьшая варианты ряда. - наименьшая варианты ряда.
Модой 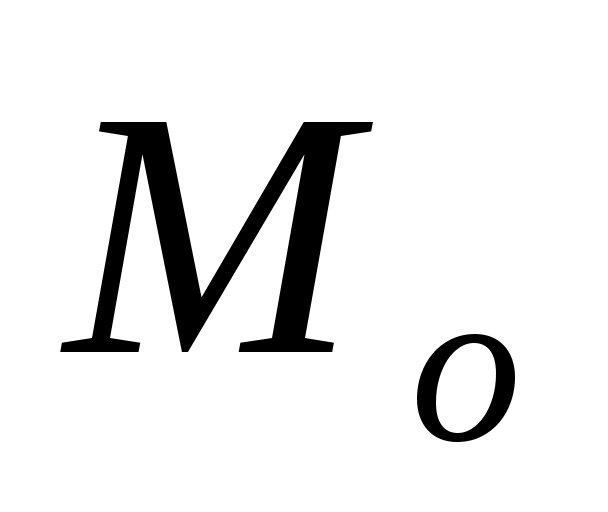 вариационного ряда называется варианта, имеющая наибольшую частоту. вариационного ряда называется варианта, имеющая наибольшую частоту.
Медианой 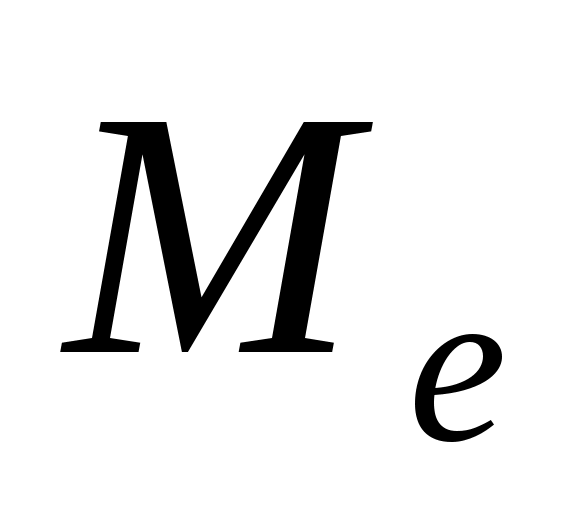 вариационного ряда называется значение признака (варианта), приходящееся на середину ряда. вариационного ряда называется значение признака (варианта), приходящееся на середину ряда.
Если 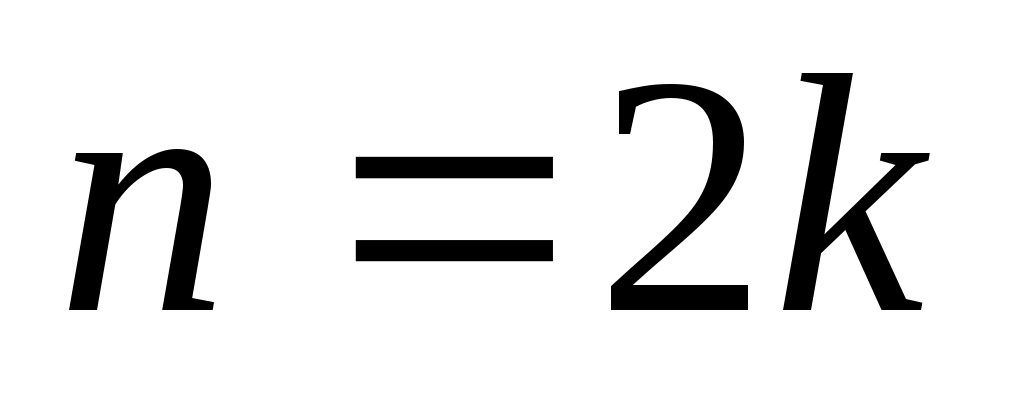 (то есть ряд (то есть ряд 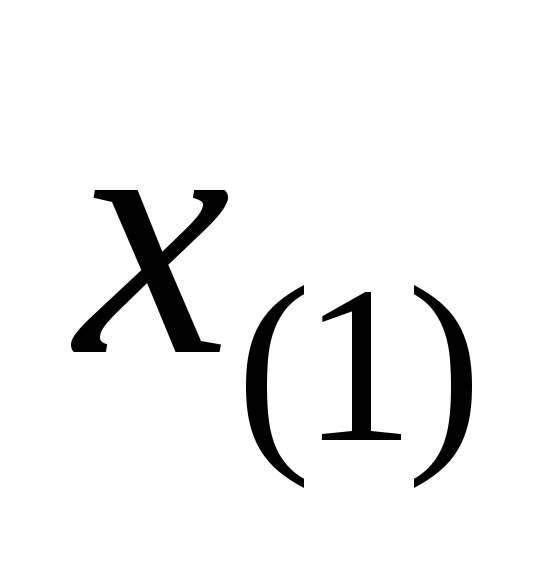 , ,  ,…, ,…, 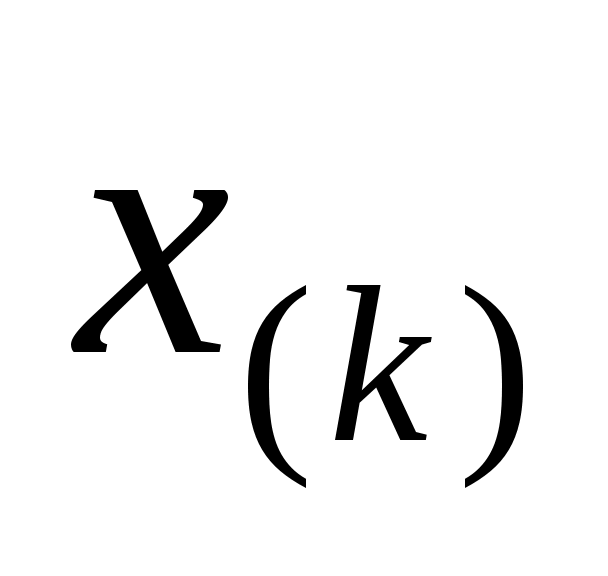 , , 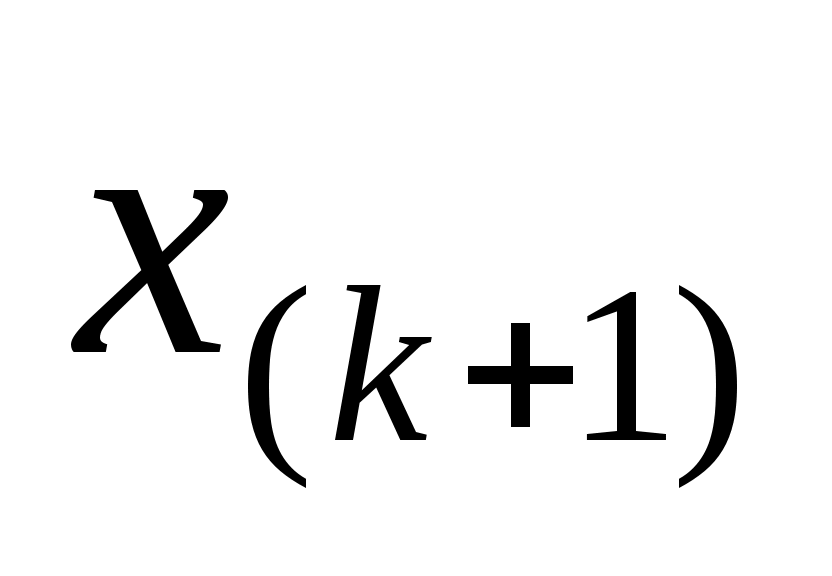 , , 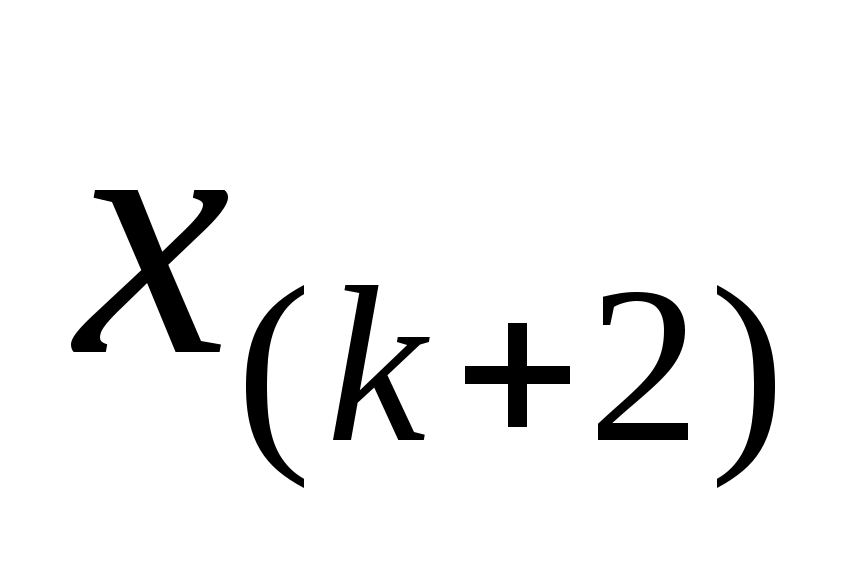 ,…, ,…, 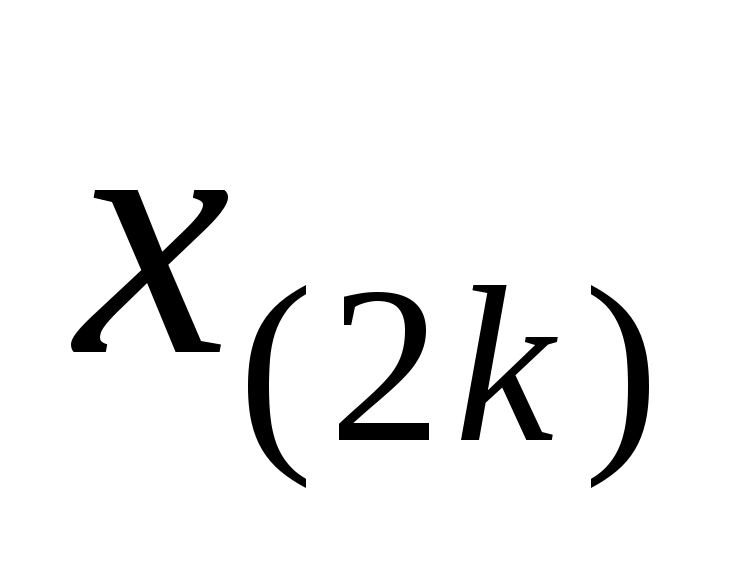 имеет четное число членов), то имеет четное число членов), то 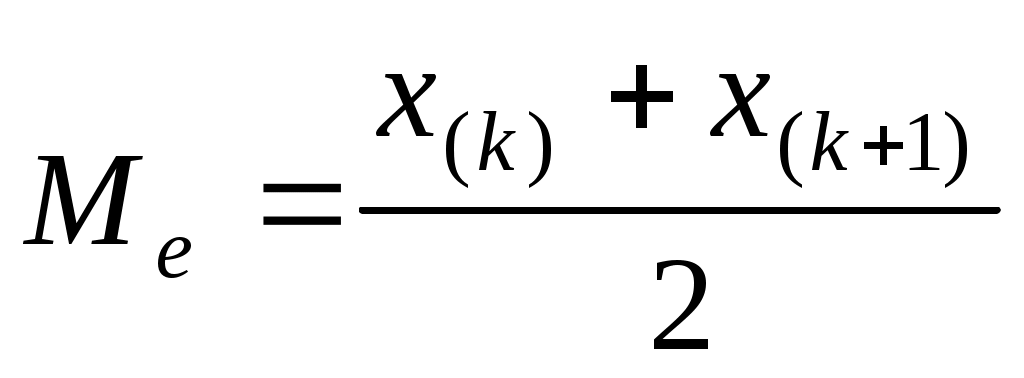 . Если . Если 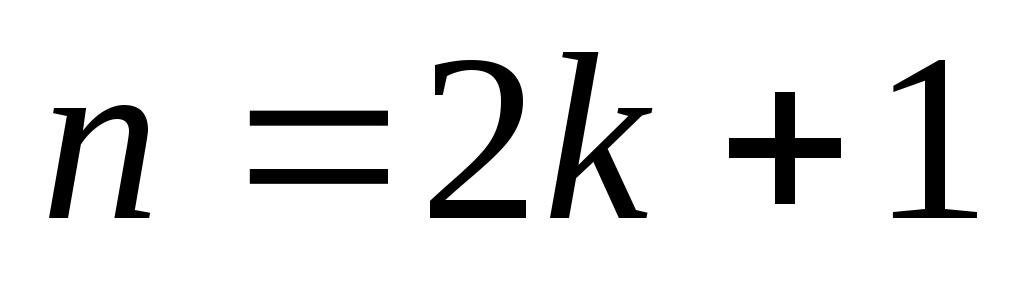 (то есть ряд имеет нечетное число членов), то (то есть ряд имеет нечетное число членов), то 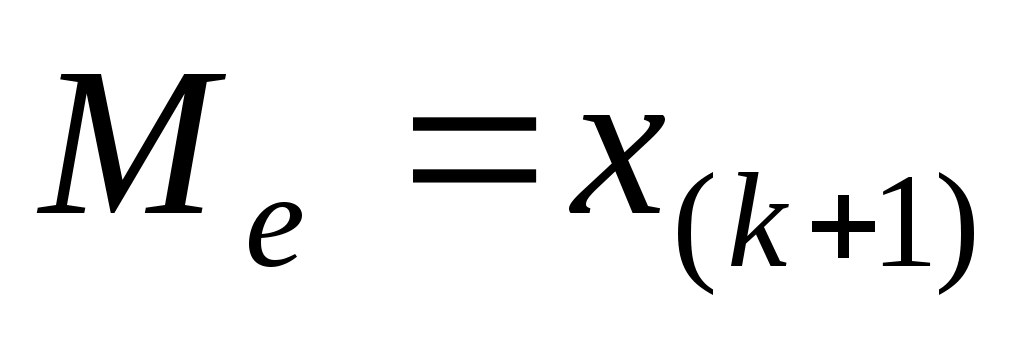 . .
Пример 9. В результате тестирования (см. пример 2) группа абитуриентов набрала баллы: 5, 3, 0, 1, 4, 2, 5, 4, 1, 5. Найти характеристики выборки.
Решение. Статистическое распределение выборки (так называемый дискретный статистический ряд) имеет вид:
Тогда:
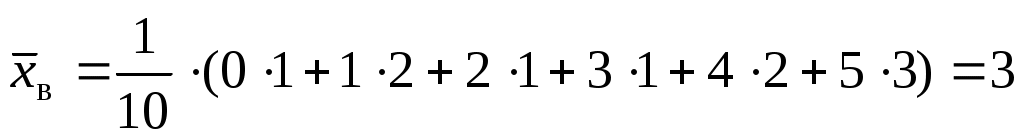 , ,
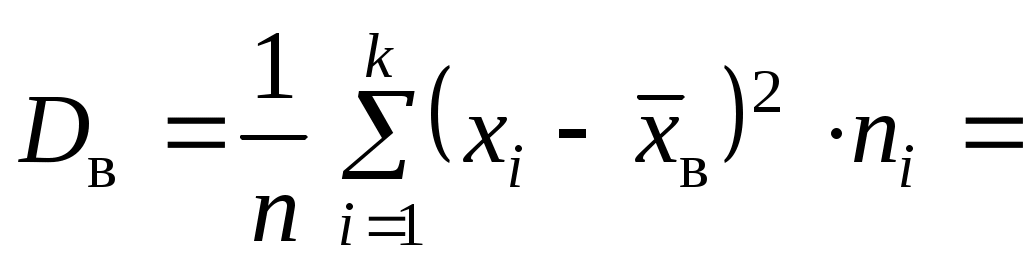
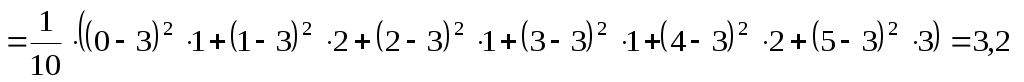 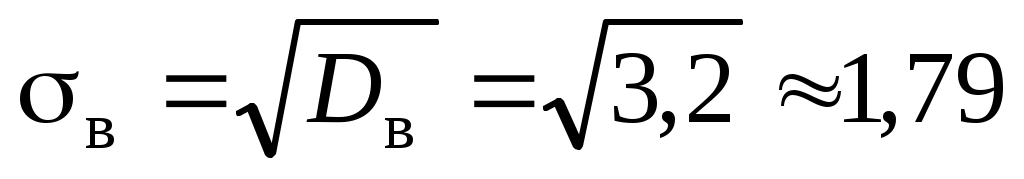 , ,
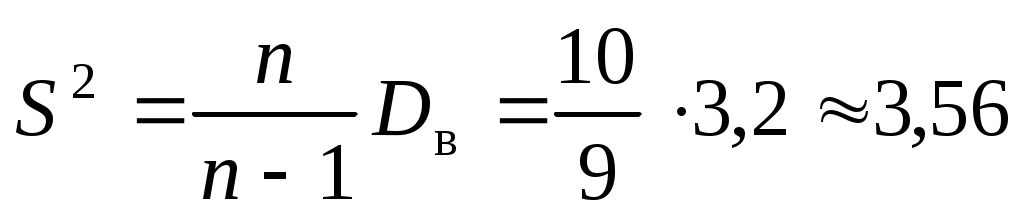 , ,
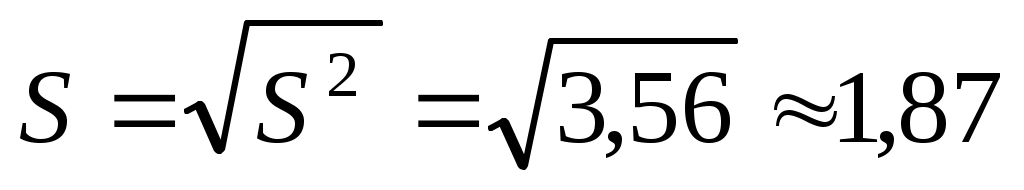 , ,
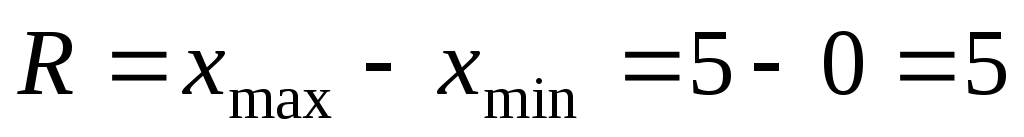 , ,
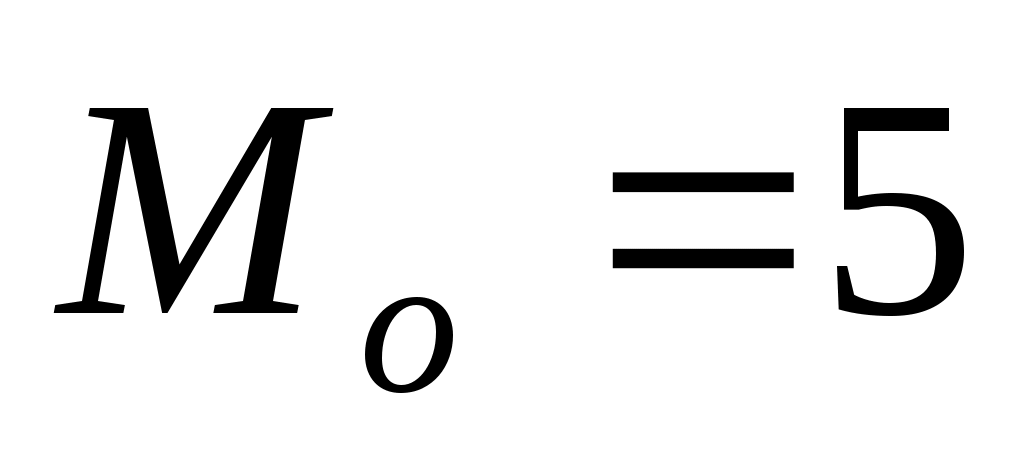 , так как 5 наиболее часто встречающаяся варианта, , так как 5 наиболее часто встречающаяся варианта,
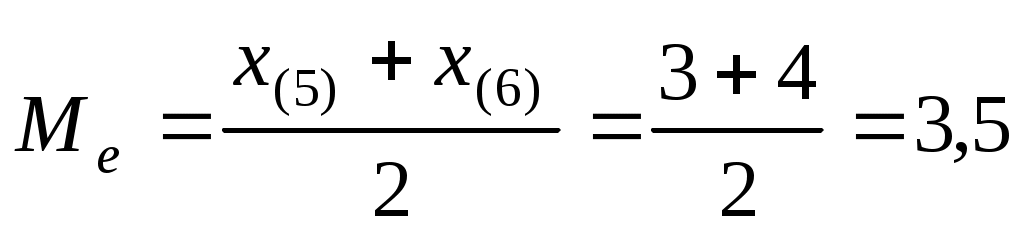 . .
Для непрерывно распределенного признака формулы для вычисления моды и медианы имеют вид:
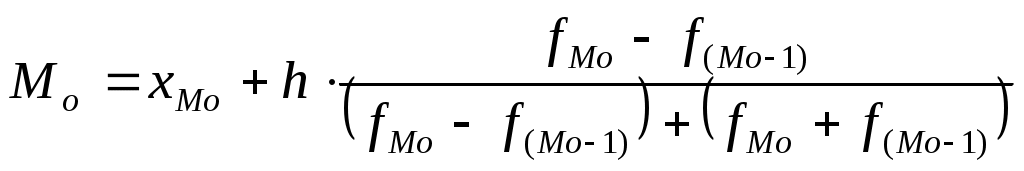 , где , где
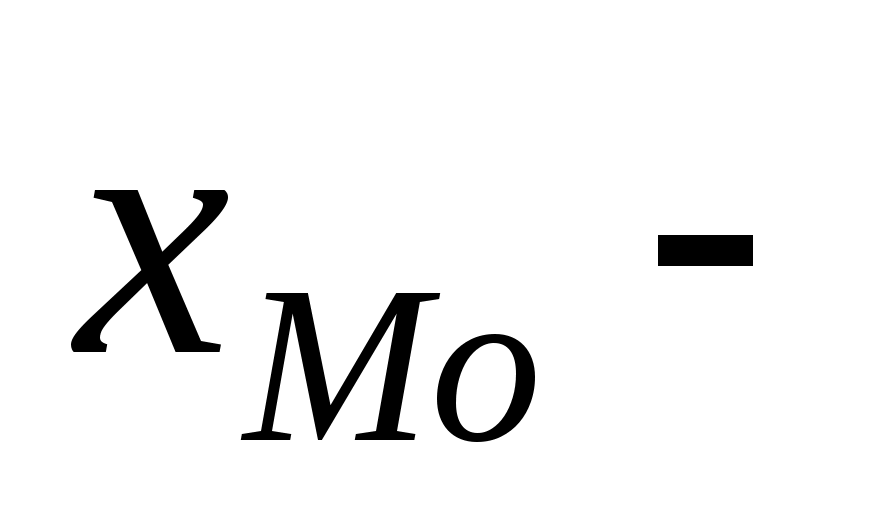 начало модального интервального интервала, то есть интервала, имеющего наибольшую частоту, начало модального интервального интервала, то есть интервала, имеющего наибольшую частоту,
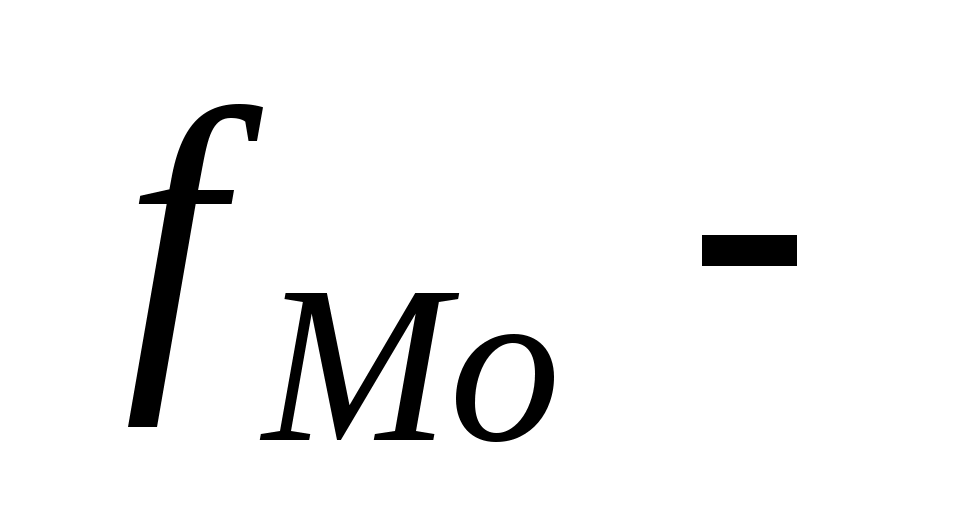 частота модального интервального, частота модального интервального,
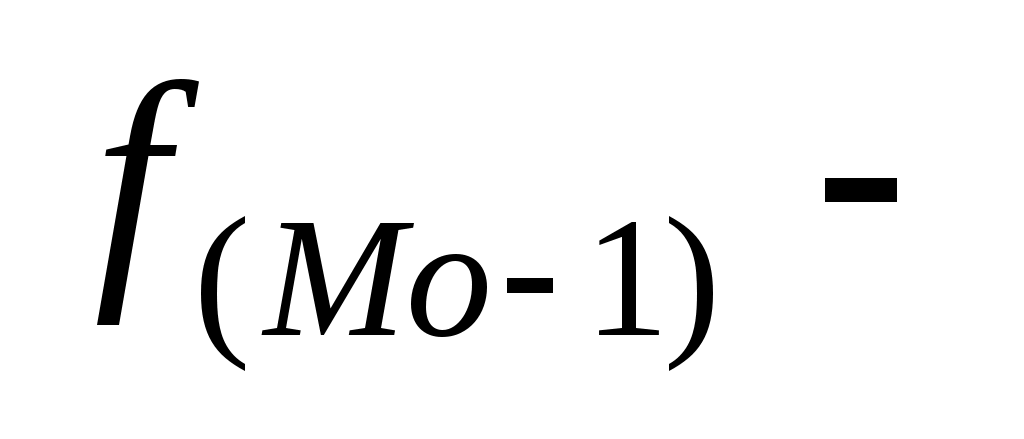 частота интервала, предшествующего модальному, частота интервала, предшествующего модальному,
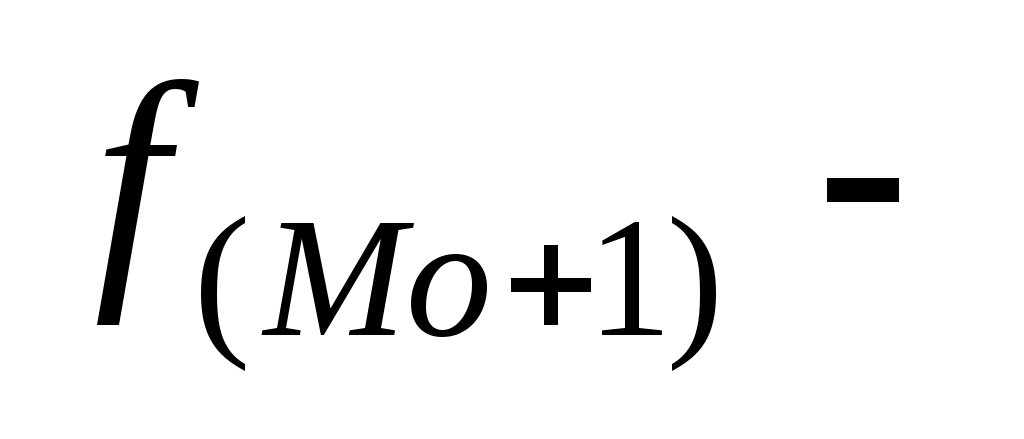 частота интервала, следующего за модальным, частота интервала, следующего за модальным,
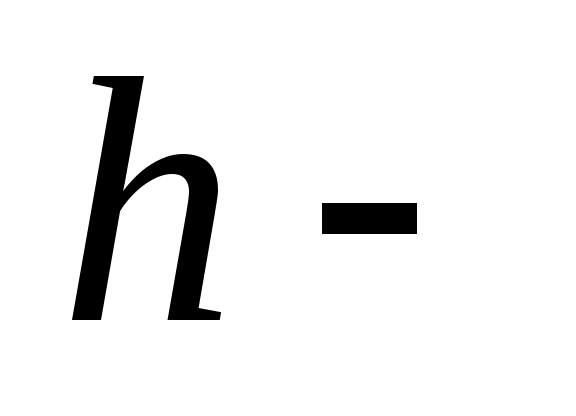 интервал группировки; интервал группировки;
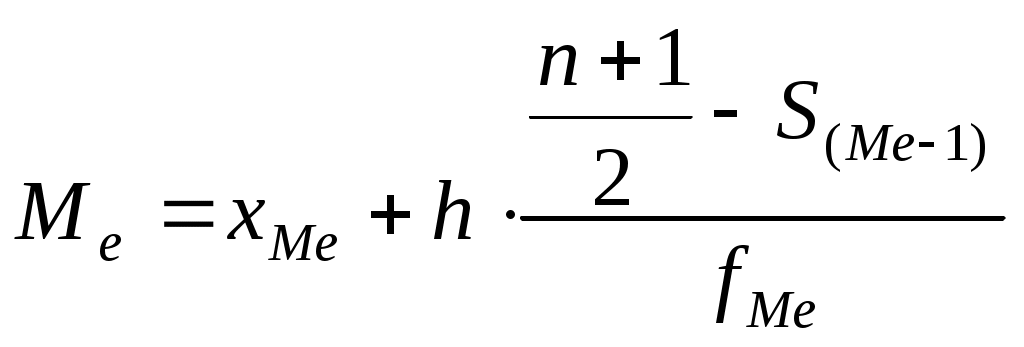 , где , где
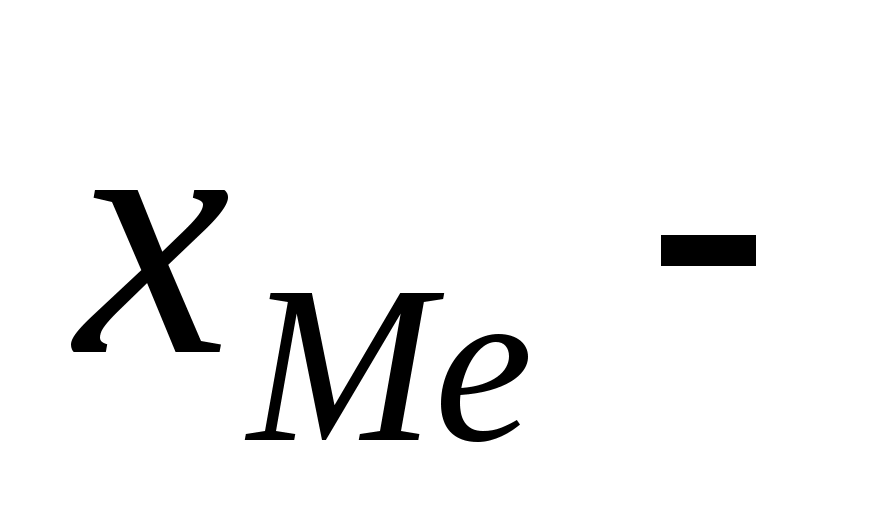 начало медианного интервала, то есть интервала содержащего серединные значения вариационного ряда, начало медианного интервала, то есть интервала содержащего серединные значения вариационного ряда,
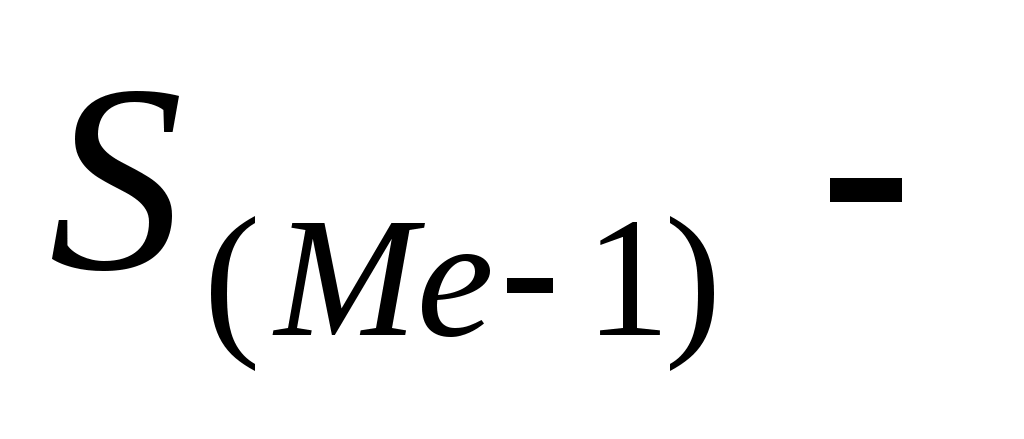 накопленная частота интервала, предшествующего модальному. накопленная частота интервала, предшествующего модальному.
|
 Скачать 1.5 Mb.
Скачать 1.5 Mb.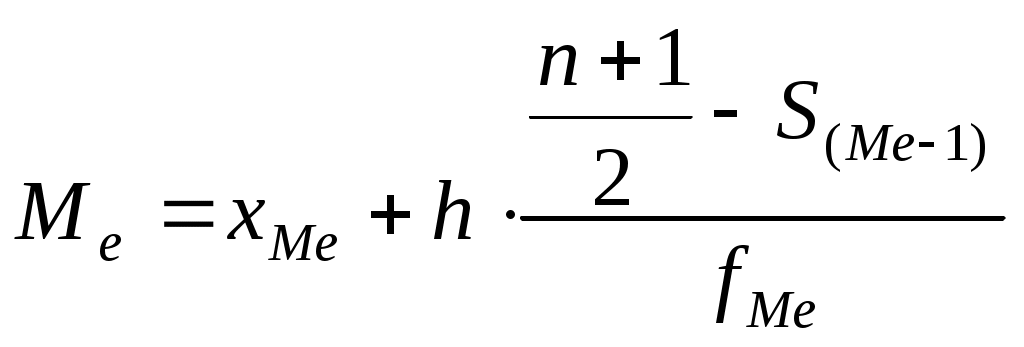 , где
, где