|
|
ргз по сопромату. Методические указания для выполнения расчетного задания
Пример 11. В условиях предыдущей задачи найти уравнение линейной регрессии, выражающее зависимость между заработной платой рабочих и числом уволившихся.
Решение.
1. Для определения параметров  и и 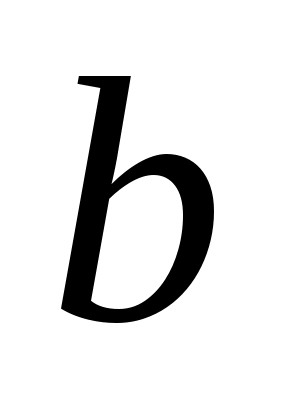 линии регрессии линии регрессии 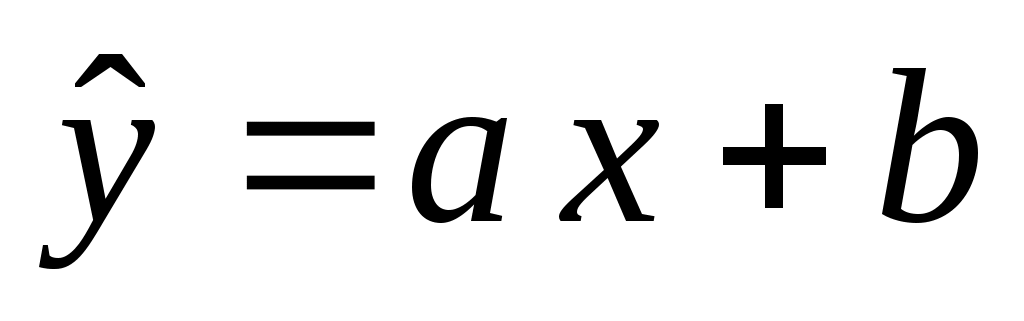 составим систему нормальных уравнений: составим систему нормальных уравнений:
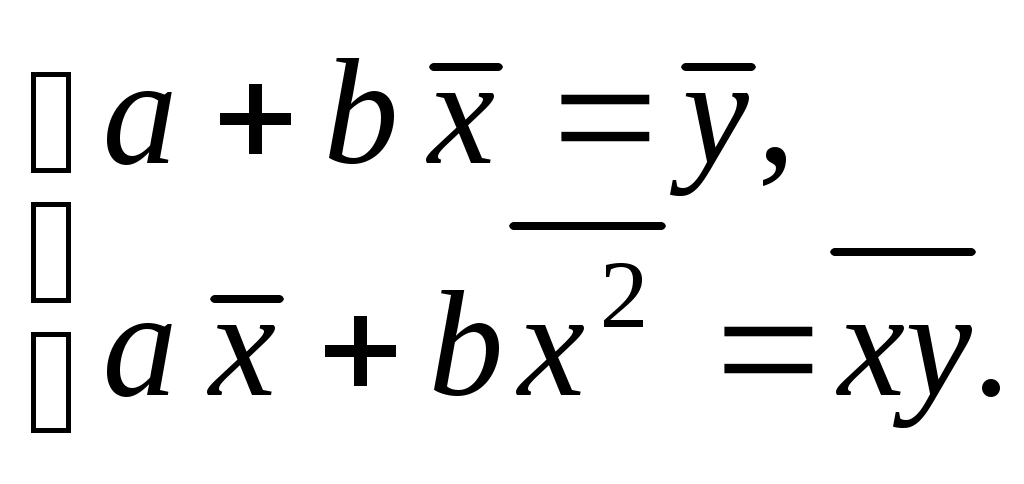
2. Подставляя найденные в предыдущей задаче средние значения 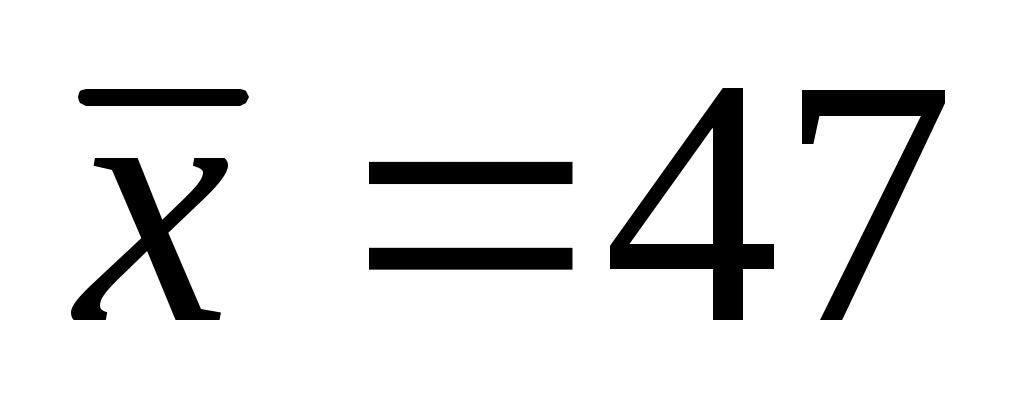 , , 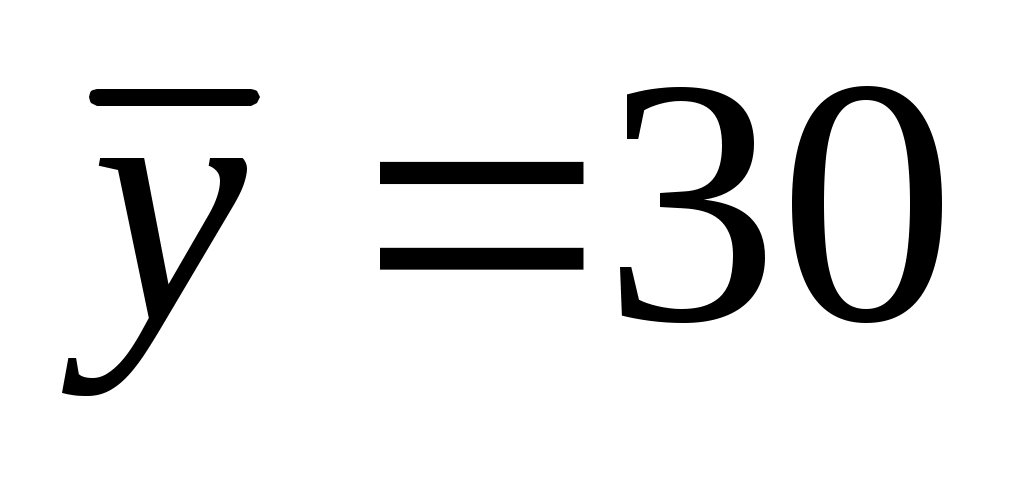 , , 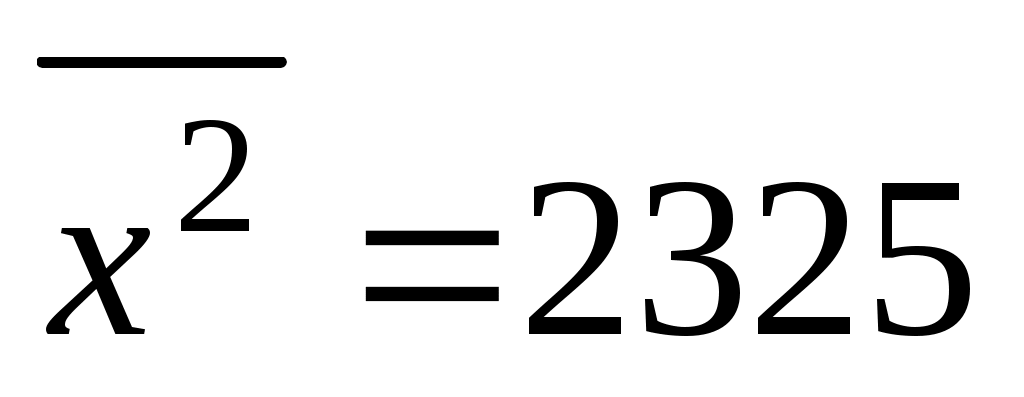 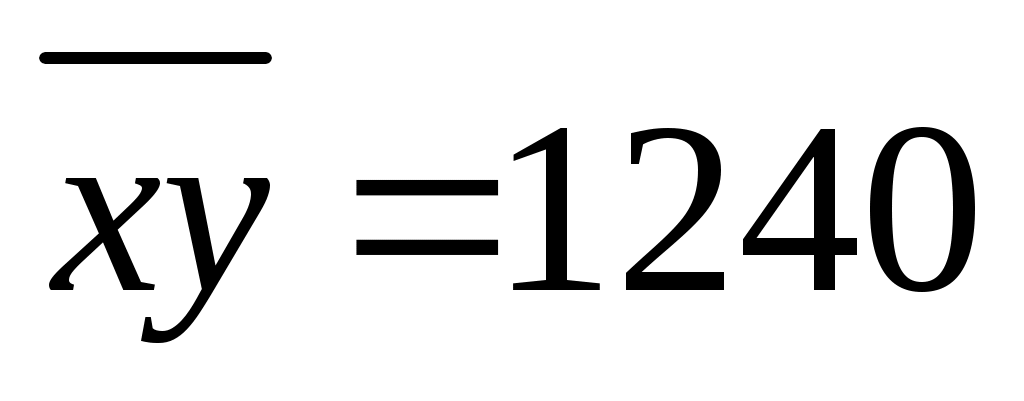 , получим: , получим:
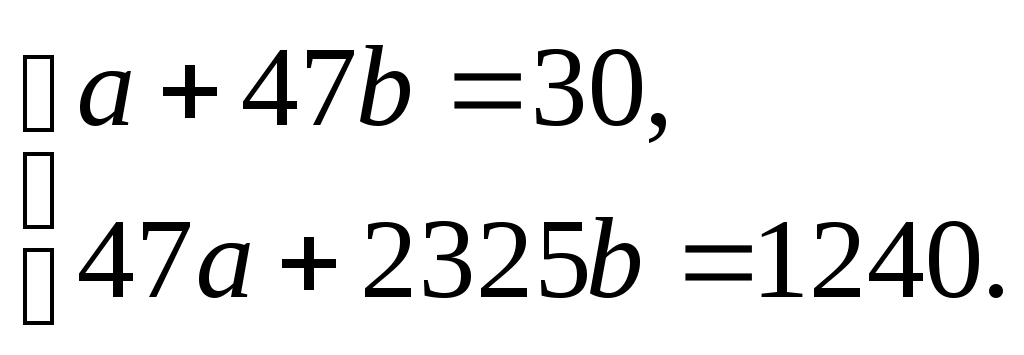
3. Решая эту систему, найдем 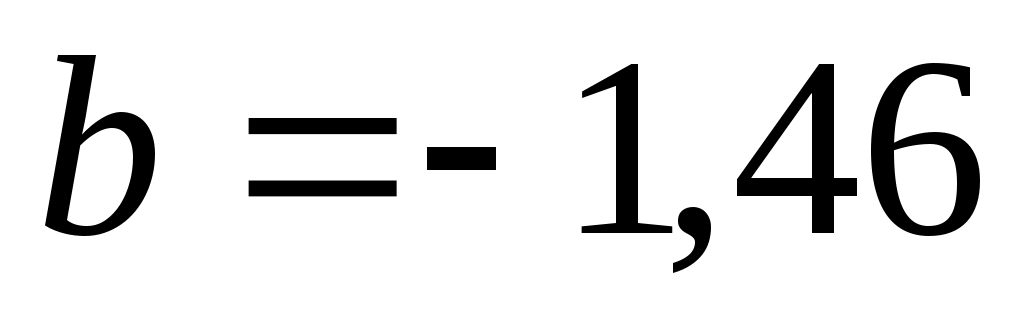 ; ; 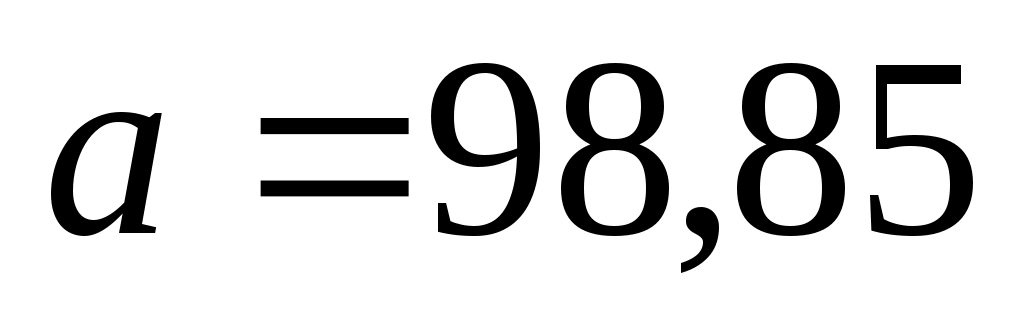 . Тогда уравнение регрессии: . Тогда уравнение регрессии:
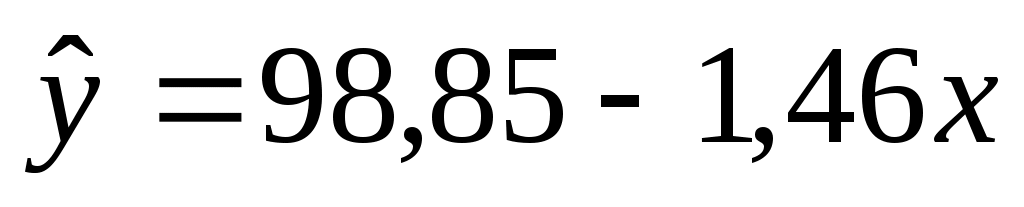 . .
Отрицательный коэффициент регрессии подтверждает то, что связь между заработной платой рабочих и текучестью кадров обратная. Вычислим коэффициент эластичности:
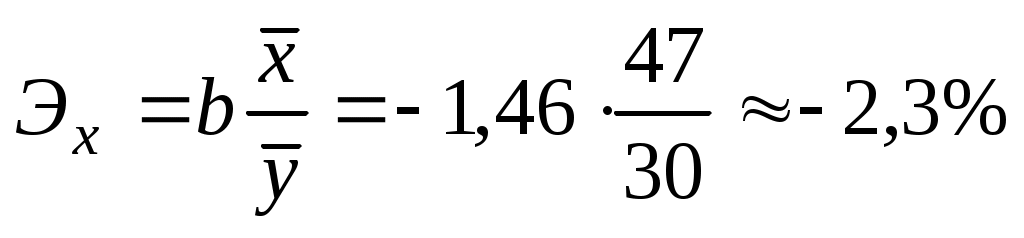 . .
Полученный коэффициент свидетельствует о том, что при увеличении заработной платы на 1%, число увольняющихся в среднем сократиться на 2,3%.
Замечание 2. Выборочную линию регрессии можно задать также при помощи линейного уравнения 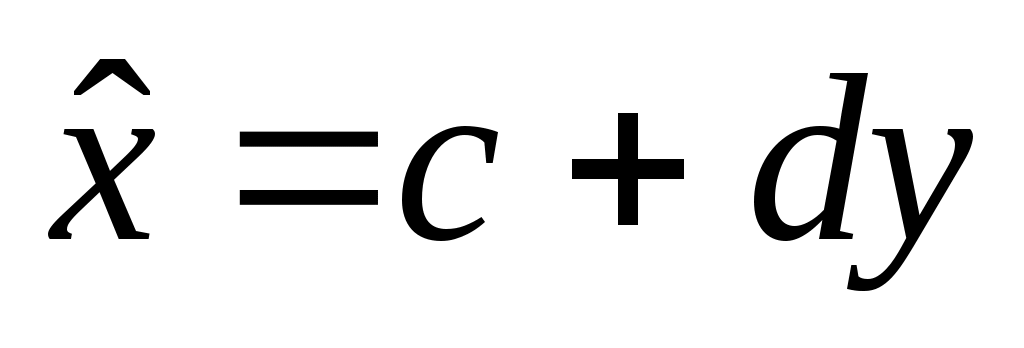 , параметры , параметры 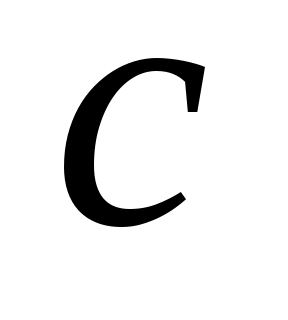 и и 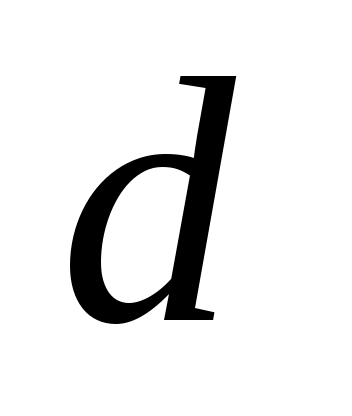 для которого находятся из системы: для которого находятся из системы:
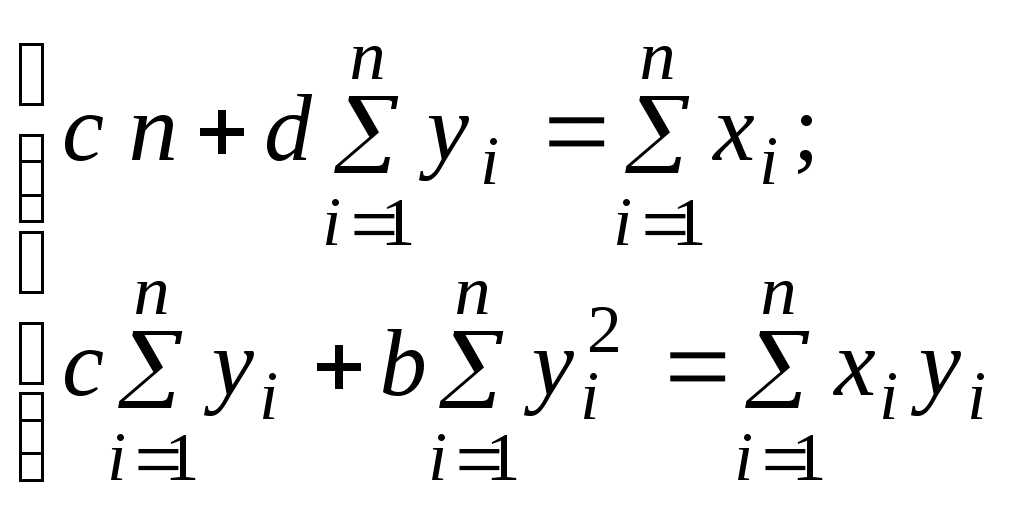 или или 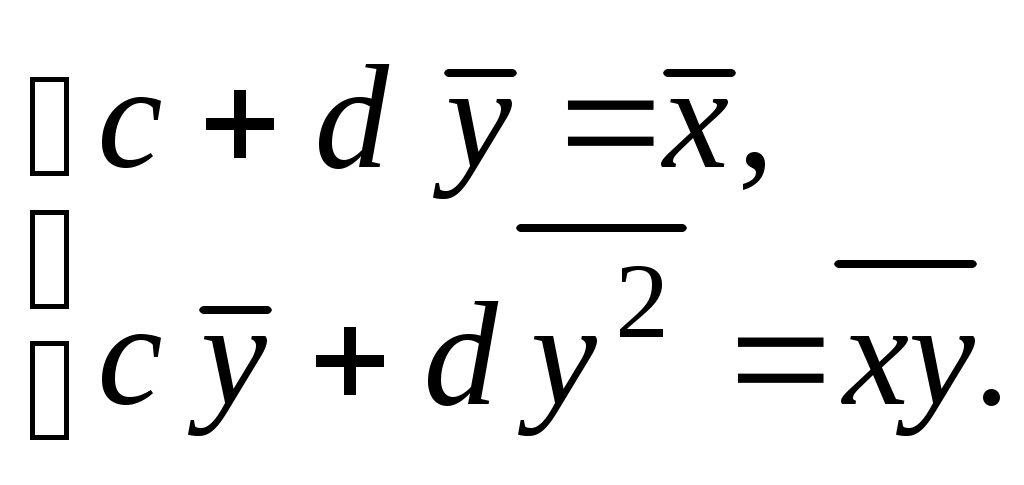
Коэффициент 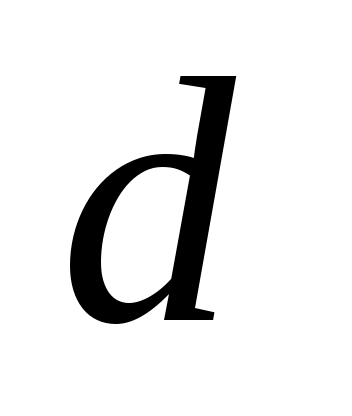 называется коэффициентом регрессии. Он показывает, на сколько единиц в среднем изменяется переменная называется коэффициентом регрессии. Он показывает, на сколько единиц в среднем изменяется переменная 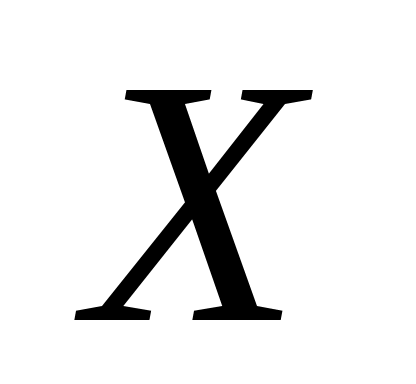 при изменении при изменении 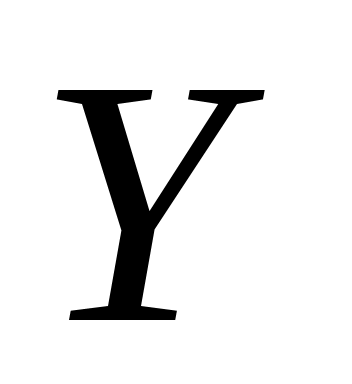 на одну единицу. на одну единицу.
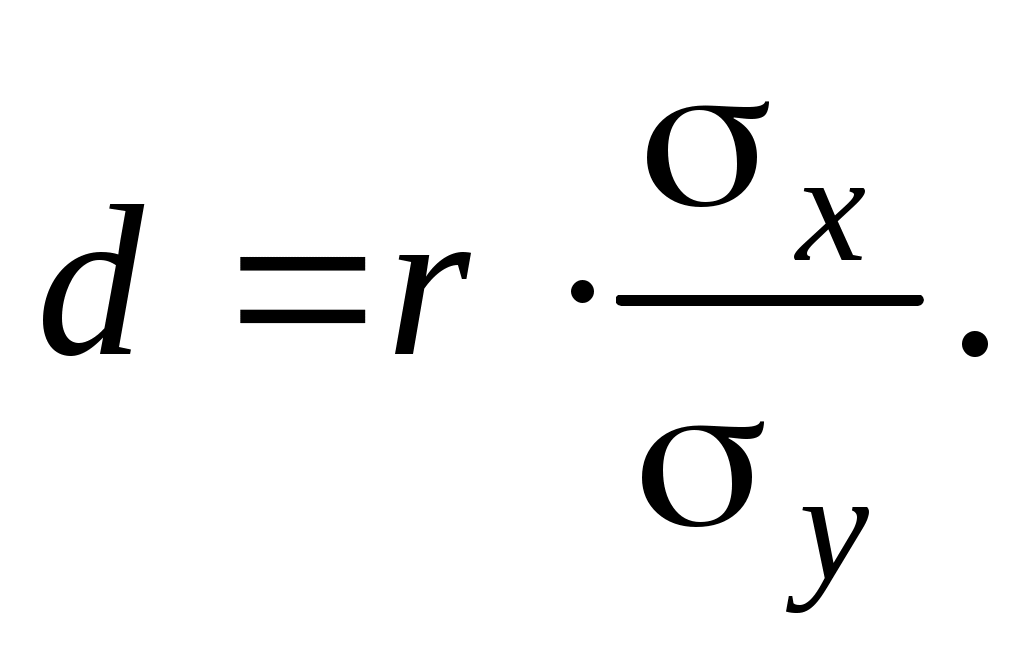
Замечание 3. Следует иметь в виду, что 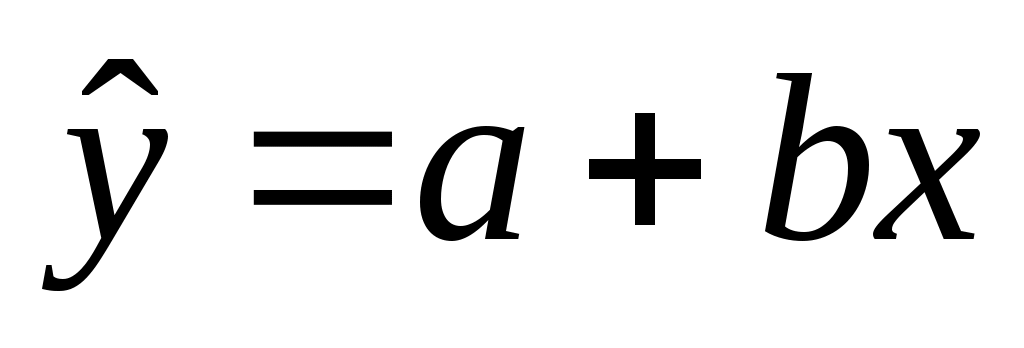 и и 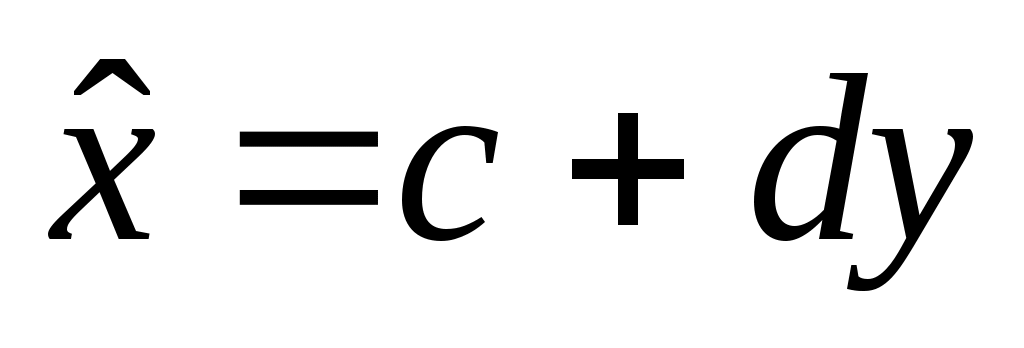 различные прямые (см. рисунок 5). Первая прямая получается в результате решения задачи о минимизации суммы квадратов отклонений по вертикали, а вторая – при решении задачи о минимизации суммы квадратов отклонений по горизонтали. Линии регрессии, заданные этими уравнениями пересекаются в точке различные прямые (см. рисунок 5). Первая прямая получается в результате решения задачи о минимизации суммы квадратов отклонений по вертикали, а вторая – при решении задачи о минимизации суммы квадратов отклонений по горизонтали. Линии регрессии, заданные этими уравнениями пересекаются в точке 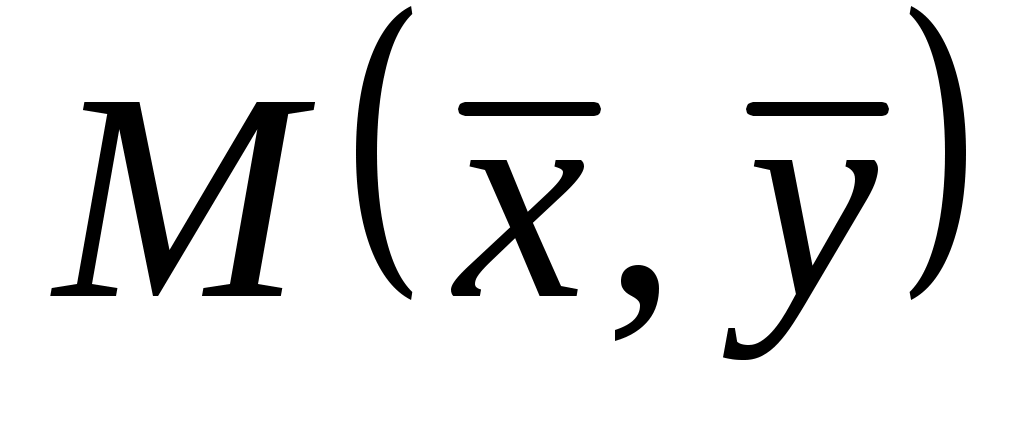 с координатами соответствующими средним значениям корреляционно связанных между собой переменных. с координатами соответствующими средним значениям корреляционно связанных между собой переменных.
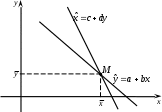
Рис. 5. Линии регрессии
Замечание 4. Если известны коэффициенты регрессии 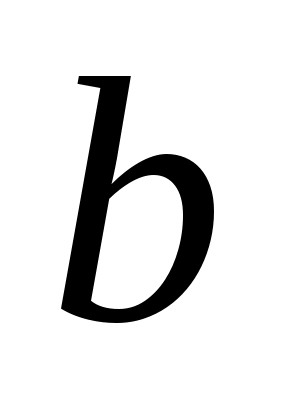 и и 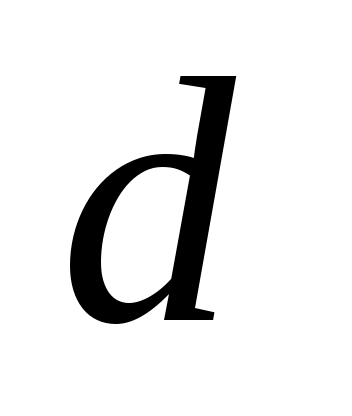 , выборочные средние , выборочные средние 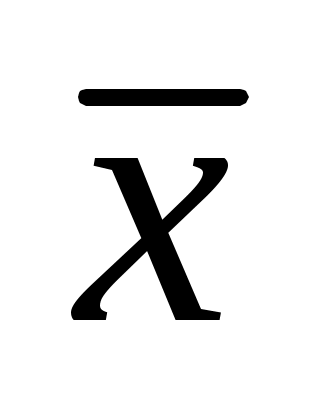 и и 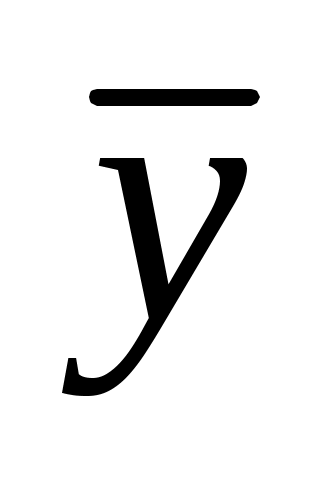 , то уравнения линейной регрессии могут быть найдены по формулам. , то уравнения линейной регрессии могут быть найдены по формулам.
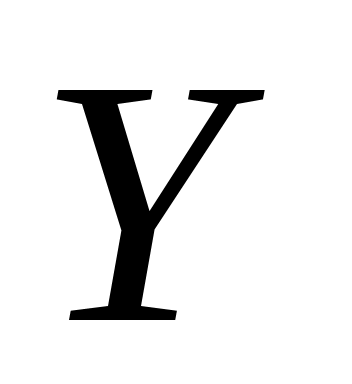 на на 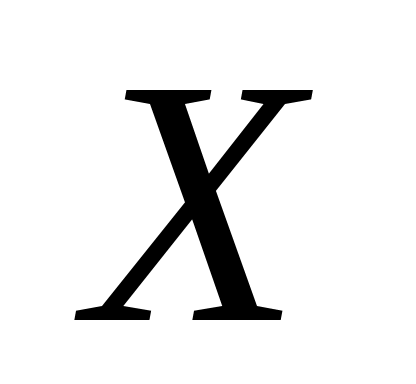 : : 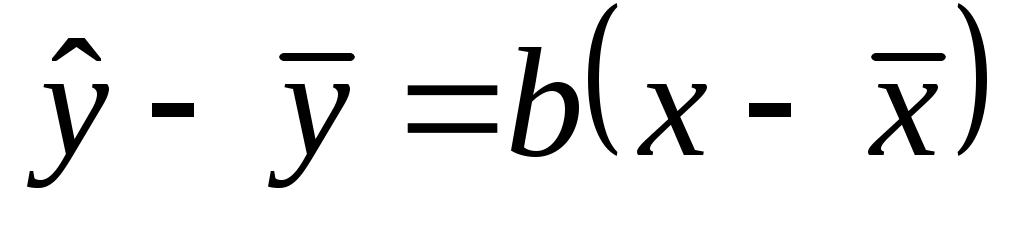 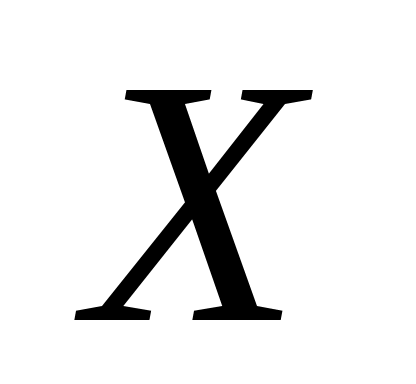 на на 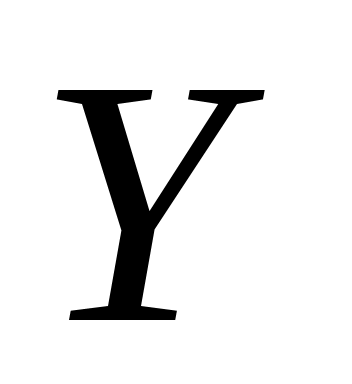 : :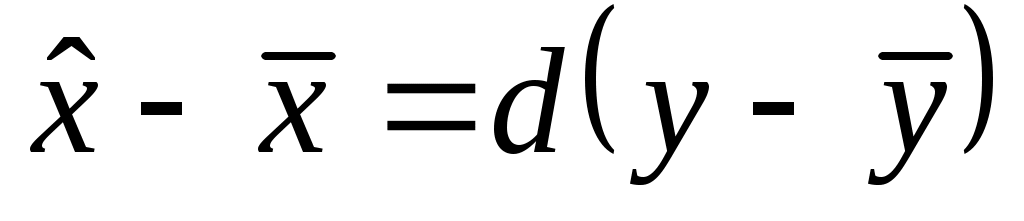
3.Задания для самостоятельной работы
Задание 1. Для выборок а), б) и в) определить размах R, моду Mo, медиану Me, выборочное среднее 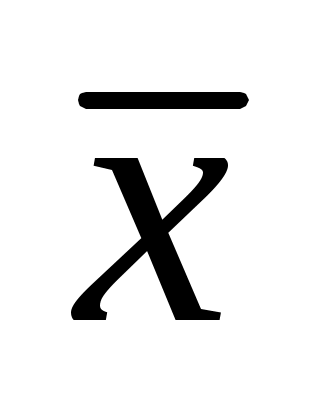 , выборочную дисперсию , выборочную дисперсию 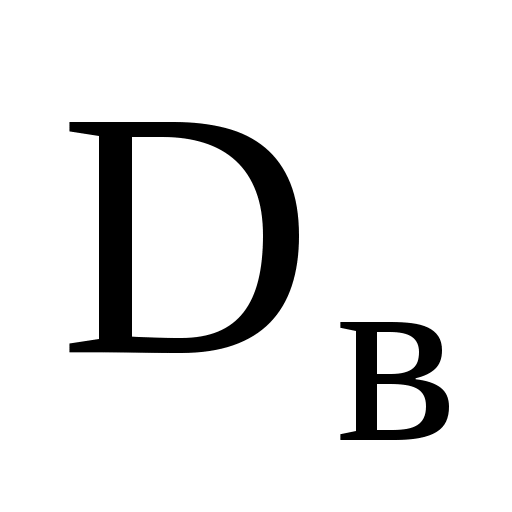 , «исправленную» выборочную дисперсию , «исправленную» выборочную дисперсию 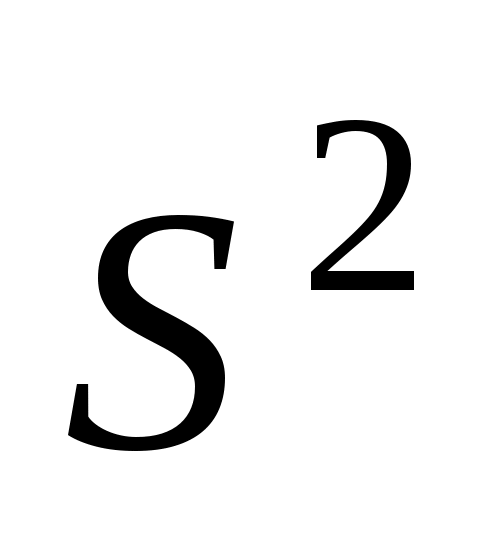 . Для a) составить вариационный и статистический ряды; для б) найти эмпирическую функцию распределения . Для a) составить вариационный и статистический ряды; для б) найти эмпирическую функцию распределения 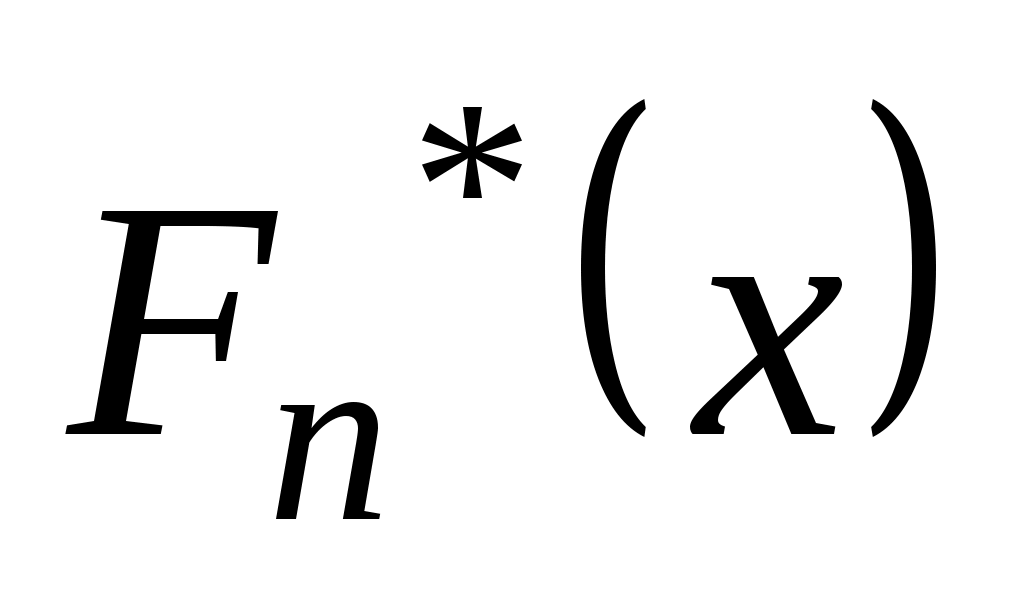 ; для в) построить гистограмму и полигон, эмпирическую функцию распределения ; для в) построить гистограмму и полигон, эмпирическую функцию распределения 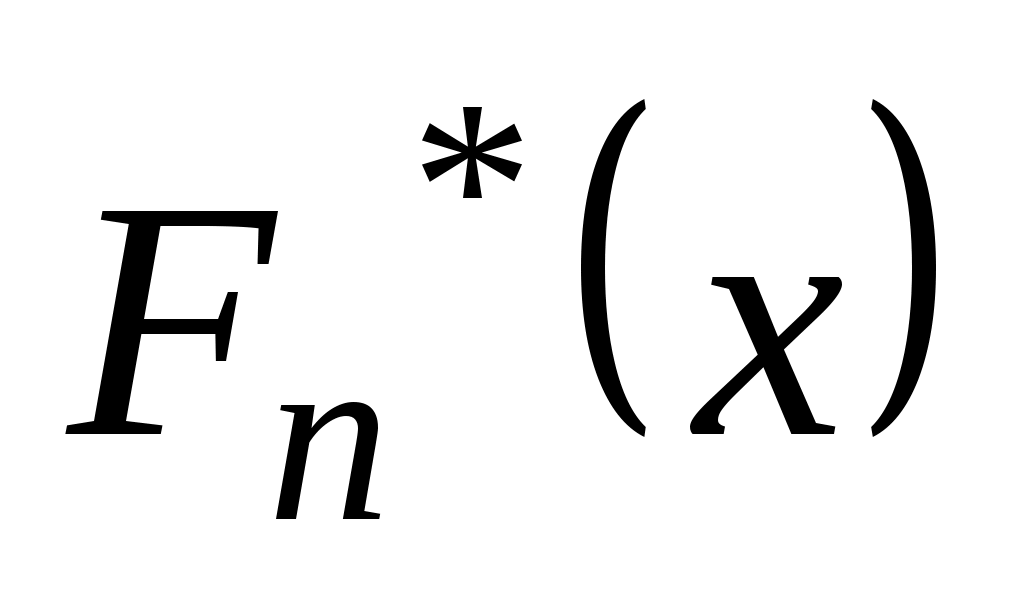 . .
а) 7, 3, 3, 6, 4, 5, 1, 2, 1, 3.
б)
|
xi
|
11
|
13
|
15
|
17
|
19
|
21
|
23
|
|
|
ni
|
2
|
4
|
8
|
12
|
16
|
10
|
3
|
|
|
|
|
|
|
|
|
|
в)
|
xi
|
[0; 4)
|
[4; 8)
|
[8; 12)
|
[12; 16)
|
[16; 20)
|
[20; 24)
|
|
ni
|
1
|
1
|
3
|
2
|
1
|
1
|
а) 6, 1, 4, 8, 5, 7, 2, 5, 7, 6.
б)
|
xi
|
12
|
14
|
16
|
18
|
20
|
22
|
23
|
|
|
ni
|
3
|
5
|
9
|
10
|
8
|
7
|
4
|
|
|
|
|
|
|
|
|
|
в)
|
xi
|
[0; 3)
|
[3; 6)
|
[6; 9)
|
[9; 12)
|
[12; 15)
|
[15; 18)
|
|
ni
|
4
|
1
|
2
|
3
|
3
|
1
|
а) 4, 9, 5, 2, 6, 9, 3, 3, 4, 9.
б)
|
xi
|
10
|
12
|
14
|
16
|
18
|
20
|
22
|
|
|
ni
|
6
|
4
|
1
|
5
|
7
|
8
|
10
|
|
|
|
|
|
|
|
|
в)
|
xi
|
[0; 6)
|
[6; 12)
|
[12; 18)
|
[18; 24)
|
[24; 30)
|
|
ni
|
2
|
3
|
1
|
1
|
2
|
а) 3, 7, 6, 4, 7, 1, 4, 2, 1, 2.
-
б)
|
xi
|
9
|
11
|
13
|
15
|
17
|
19
|
21
|
|
|
ni
|
9
|
5
|
4
|
7
|
8
|
10
|
6
|
|
|
|
|
|
|
|
|
в)
|
xi
|
[0; 5)
|
[5; 10)
|
[10; 15)
|
[15; 20)
|
[20; 25)
|
|
ni
|
1
|
3
|
4
|
2
|
1
| |
|
|
 Скачать 1.5 Mb.
Скачать 1.5 Mb.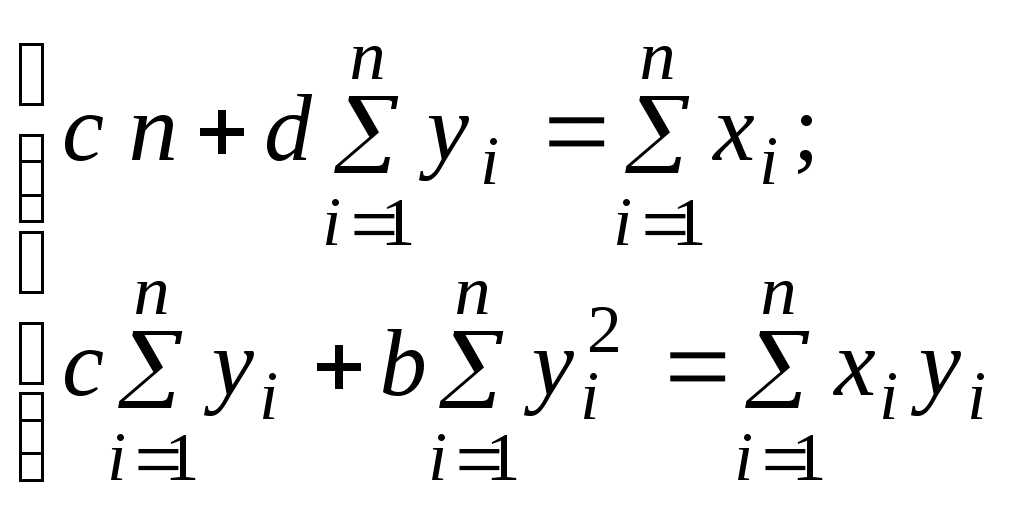 или
или 
