ргз по сопромату. Методические указания для выполнения расчетного задания
 Скачать 1.5 Mb.
|
|
Коэффициент корреляции рассчитывается по формуле:  .Найдем средние значения:  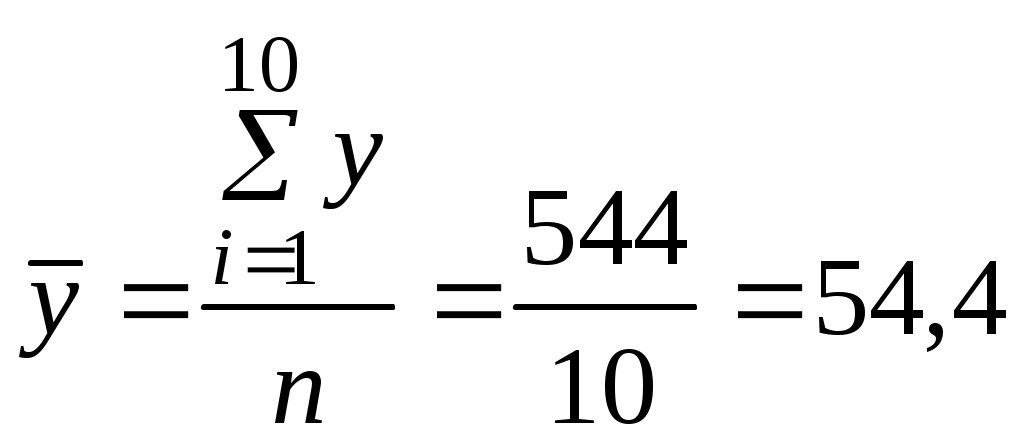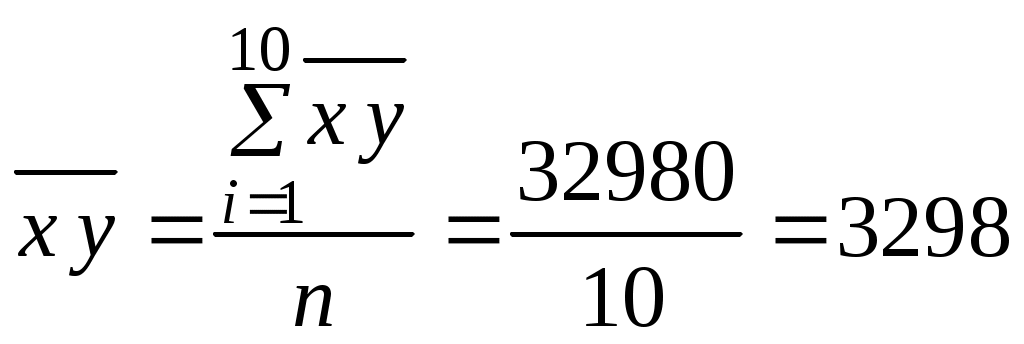(сумма значений второго столбца, деленная на число строк): ; (сумма значений третьего столбца, деленная на число строк): ; (среднее значение шестого столбца): .Найдем средние квадратические отклонения  и  :  ,где  рассчитывается как среднее значение четвертого столбца. , Где  – среднее значение пятого столбца.Подставляя найденные значения в формулу коэффициента корреляции, получим:  .2. Составим уравнения линейной регрессии.  и  .Для определения параметров  и  линии регрессии  составим систему нормальных уравнений: Подставляя найденные в пункте 1 задачи средние значения  ,  ,  ,  , получим: Решая эту систему, найдем  и  . Тогда уравнение регрессии и имеет вид: . и .Составим уравнения линейной регрессии и используя формулы:  и  .  или  .3. Построим корреляционное поле и графики прямых линий регрессии Y на Х и Х на Y (рис. 10). Из чертежа видно, что полученные уравнения хорошо согласуются с исходными данными. 4. По вычисленным коэффициентам, можно сделать вывод, что связь между температурой реакции и выходом продукта прямая и очень тесная, так как полученный коэффициент корреляции (  ) положительный и очень близок к единице. Это говорит о том, что чем больше температура реакции ( ), тем больше выход продукта ( ).Выясним, какая часть вариации обусловлена вариацией , для этого вычислим коэффициент детерминации: .То есть вариация выхода продукта ( ) на 94% обусловлена вариацией температурой реакции ( ).Положительный коэффициент регрессии подтверждает то, что связь между температурой реакции и выходом продукта прямая. Вычислим коэффициент эластичности (регрессии): .Полученный коэффициент свидетельствует о том, что при увеличении температуры реакции на 1%, выход продукта в среднем увеличится на 2,1 %.  Рис. 6. Корреляционное поле. Линии регрессии Спрогнозируем выход продукта при  С. Так как при увеличении температуры реакции на 1%, выход продукта в среднем увеличится на 2,1 %, то увеличение температуры реакции до С (т.е. примерно на 5,3%) должно привести к увеличению выхода продукта примерно на 11,1% (т.е примерно на 11,1 кг/ч). Подставляя в уравнение регрессии значение  , получим  , т.е. при температуре реакции С получим выход продукта 111,75 кг/ч, т.е на 11,75 кг/ч больше.Рекомендательный библиографический список Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М., Высшая школа, 1979, 400 с. Гмурман В.Е. Теория вероятностей и математическая статистика. – М., Высшая школа, 197, 368 с. Горелова Г.В., Кацко И.А. Теория вероятностей и математическая статистика в примерах и задачах с применением EXCEL: Учебное пособие для вузов.– Ростов н/Д, Феникс, 2005,112 с. Господариков А.П., Ивакин В.В., Лебедев И.А., Зацепин М.А. Высшая математика. Теория вероятностей и основы математической статистики. Учебное пособие.‑ Горный университет, 2013. Кремер Н.Ш. Теория вероятностей и математическая статистика: Учебное пособие для вузов – М., Юнити-Дана, 2000, 543 с. Палий И.А. Прикладная статистика: Учеб. Пособие для вузов./ И.А. Палий – М.: Высш. Шк., 2004. – 176 с. СОДЕРЖАНИЕ
|