ргз по сопромату. Методические указания для выполнения расчетного задания

• Название: Методические указания для выполнения расчетного задания
• Анкор: ргз по сопромату
• Дата: 15.05.2022
• Размер: 1.5 Mb.
• Имя файла: Rgz_Dlya_Gr_To-20_Vd-20_Bts-20_Mo-20.doc
• Тип: Методические указания; #530094
• страница: 4 из 10

2. Корреляционно-регрессионный анализ

2.1 Понятие о корреляционной и регрессионной связи

Проводя исследования, необходимо считаться с взаимосвязью наблюдаемых процессов и явлений. При этом полнота описания, так или иначе, определяется количественными характеристиками причинно-следственных связей между ними. Оценка наиболее существенных из них, а также воздействия одних факторов на другие является одной из основных задач статистики. Изучение реальных процессов обычно предполагает наблюдение над целым рядом случайных величин. Возникает задача изучения взаимосвязи между случайными величинами. Формы проявления взаимосвязей разнообразны.

Различают два вида зависимостей между явлениями: функциональную и корреляционную (статистическую).

При функциональной зависимости каждому значению независимой переменной соответствует вполне определенное значение зависимой переменной .

В большинстве случаев между переменными величинами существуют зависимости, когда каждому значению одной переменной соответствует не какое-то определенное, а множество возможных значений другой переменной. Иначе говоря, каждому значению одной переменной соответствует определенное (условное) распределение другой переменной. Такая зависимость называется статистической (или стохастической, вероятностной)

Статистическую зависимость называют корреляционной, если при изменении значений одной величины меняется среднее значение другой. Если переменные не равноправны, т.е. четко ясно, какая из них причина, какая – следствие, то такая зависимость, при которой одна из переменных служит причиной изменения другой, называется регрессионной.

При сравнении функциональных и корреляционных зависимостей следует иметь в виду, что при функциональной зависимости, зная , можно вычислить величину , а при корреляционной зависимости устанавливается лишь тенденция изменения при изменении .

Статистические связи между переменными можно изучать методами корреляционного и регрессионного анализа. Основной задачей регрессионного анализа является установление формы и изучение зависимости между переменными. Основной задачей корреляционного анализа – выявление связи между случайными величинами и оценка тесноты связи.

2.2 Коэффициент корреляции

Для характеристики корреляционной зависимости между случайными величинами вводится понятие коэффициента корреляции .

Коэффициент корреляции между двумя случайными величинами и вычисляется по формуле:

,

где , – средние квадратические отклонения случайных величин соответственно.

Отметим некоторые свойства коэффициента корреляции:

1. 
   Если независимые случайные величины, то коэффициент корреляции равен нулю.
   
2. 
   Коэффициент корреляции принимает значения на отрезке , то есть . В зависимости от того, насколько приближается к 1, в математической статистике различают (шкала Шеддока): связи нет ( ), связь слабую ( ), умеренную ( ), тесную и очень тесную .
   
3. 
   Если , то между случайными величинами имеет место функциональная, а именно линейная зависимость.
   
4. 
   Коэффициент корреляции указывает на направление связи. Если , то связь прямая, если отрицателен, то это свидетельствует о наличии обратной связи.
   

Квадрат коэффициента корреляции называется коэффициентом детерминации:

.

Коэффициент детерминации показывает, какая часть общей вариации обусловлена вариацией .

Пример 10. С целью анализа влияния заработной платы на текучесть рабочей силы на пяти однотипных предприятиях проведены измерения уровня зарплаты (тыс. руб.) и числа уволившихся за год рабочих :

	30	40	50	55	60
	60	35	20	20	15

Определить степень влияния заработной платы на текучесть рабочей силы.

Решение. Для определения тесноты связи вычислим коэффициент корреляции, для чего составим расчетную таблицу:

1	2	3	4	5	6
1	30	60	900	3600	1800
2	40	35	1600	1225	1400
3	50	20	2500	400	1000
4	55	20	3025	400	1100
5	60	15	3600	225	900
	235	150	11625	5850	6200

Так как коэффициент корреляции рассчитывается по формуле

, то:

1. Найдем средние значения: 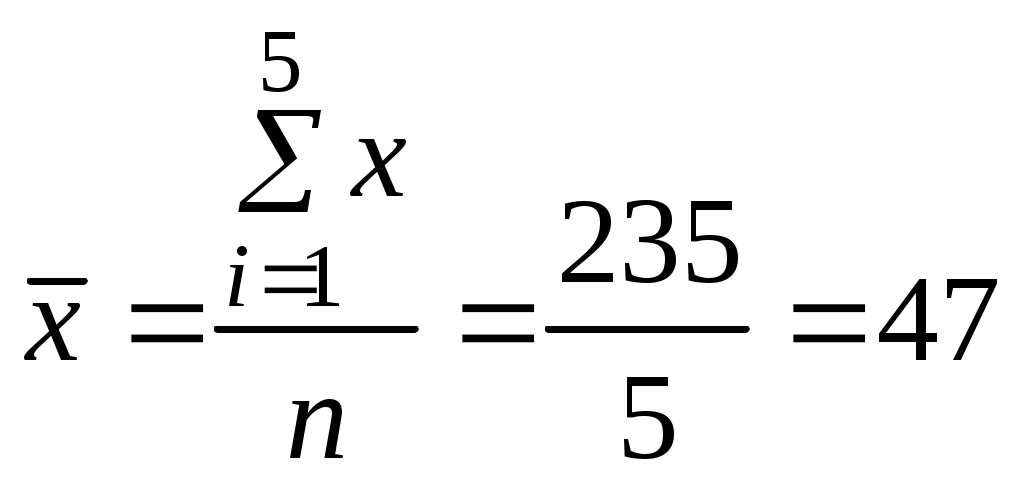(сумма значений второго столбца, деленная на число строк:

;

среднее значение (сумма значений третьего столбца, деленная на число строк):

;

среднее значение 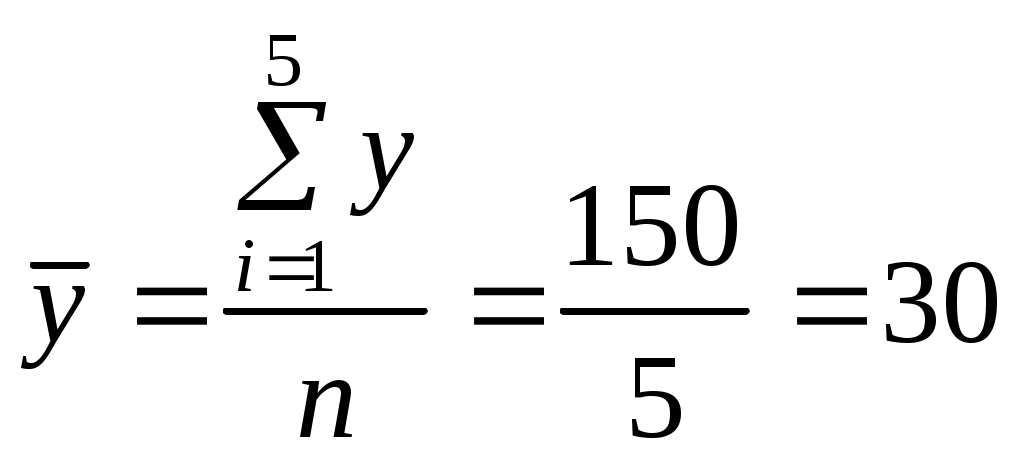(среднее значение 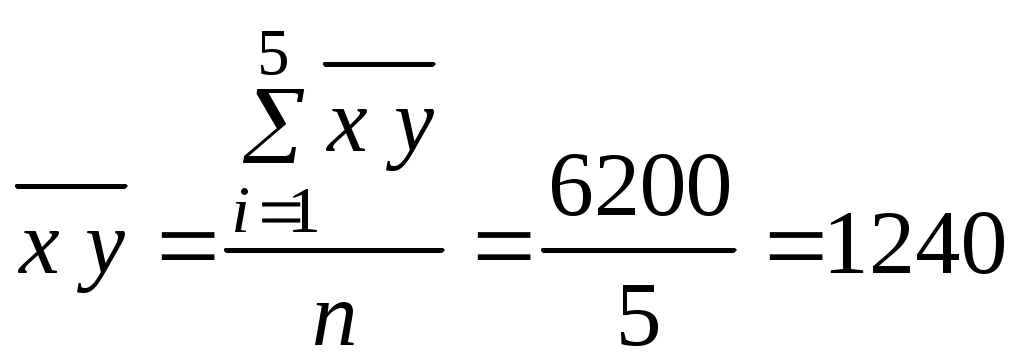шестого столбца):

.

2. Найдем средние квадратические отклонения :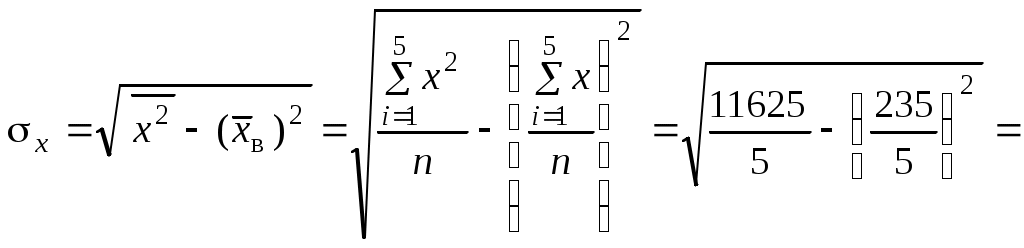



.

где рассчитывается как среднее значение четвертого столбца.

Аналогично ,

где – среднее значение пятого столбца.

3. Подставляя найденные значения в формулу коэффициента корреляции, получим

.

Таким образом, можно сделать вывод, что связь между заработной платой и текучестью рабочей силы очень тесная и обратная, так как полученный коэффициент корреляции отрицательный. Это говорит о том, что чем меньше заработная плата ( ), тем больше число уволившихся.

Выясним, какая часть вариации обусловлена вариацией . Вычислим коэффициент детерминации:

.

То есть вариации текучести рабочей силы ( ) на 92% обусловлена вариацией заработной платы ( ).

2.3 Линейная парная регрессия

После того, как с помощью корреляционного анализа выявлено наличие статистических связей между переменными и оценена степень тесноты, обычно переходят к математическому описанию вида зависимостей с использованием регрессионного анализа. Если коэффициент корреляции , то согласно шкале Шеддока связи между переменными нет, а следовательно не имеет смысла описывать модель связи.

Регрессионная модель представляет собой математическое выражение, связывающее случайные величины . Уравнение регрессии – это зависимость величины от .

Часто встречающейся моделью зависимости является линейная парная корреляция. Вообще говоря, уравнение регрессии может описывать взаимосвязь не двух, а более переменных (то есть быть не парной, а множественной). Кроме того, связь между переменными далеко не всегда линейна.

В общем случае уравнение регрессии имеет вид:

,

где параметры модели, ошибка наблюдений.

Уравнение парной линейной регрессии выглядит следующим образом:

,

где a и b- параметры уравнения линейной регрессии.

Для нахождения параметром применяют метод наименьших квадратов, согласно которому неизвестные a и b выбираются таким образом, чтобы сумма квадратов отклонений эмпирических средних значений от значений, найденных по уравнению регрессии была минимальной:

.

Получим систему нормальных уравнений для нахождения искомых параметров: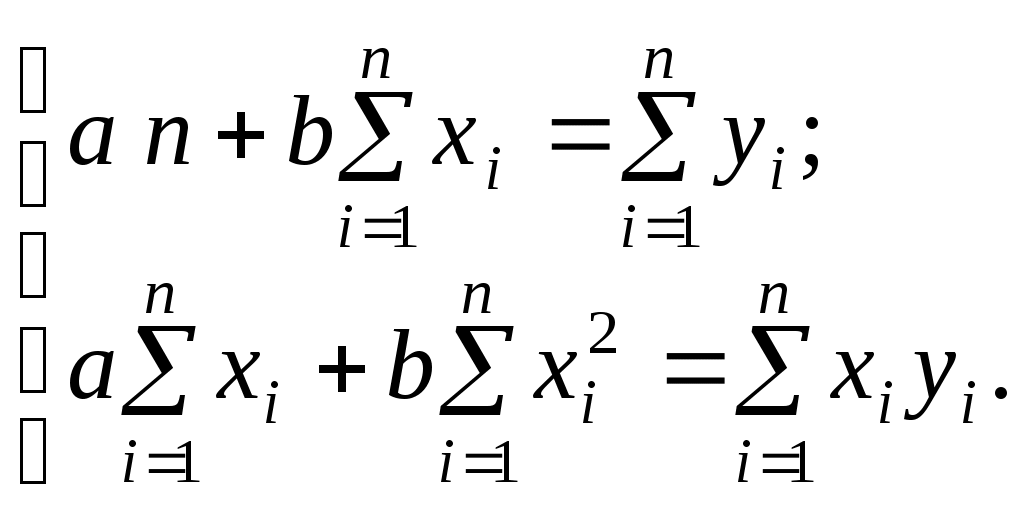



Разделив обе части уравнений на , получим систему нормальных уравнений в виде:



Решая систему уравнений, найдем:



зная, что и формулу для вычисления коэффициента корреляции можем записать:



Коэффициент называется коэффициентом регрессии. Он показывает, на сколько единиц в среднем изменяется переменная при изменении на одну единицу.

Замечание 1. Знак коэффициента регрессии указывает на направление связи: если , связь прямая, если - обратная. Очевидно, что знаки коэффициентов корреляции и регрессии должны совпадать.

Решая систему относительно параметра , получим:

.

Для установления влияния на зависимую переменную независимой переменной, то есть для интерпретации модели используется коэффициент эластичности:

.

Коэффициент эластичности показывает, на сколько процентов изменится при изменении на 1 %.