Математика. Б1.Б.11_ММ Математика 38.03.02. Методические указания и задания к занятиям семинарского типа, контрольной и самостоятельной работе по дисциплине математика
 Скачать 2.28 Mb. Скачать 2.28 Mb.
|
|
Методические указания к решению задач 41 – 50 Неопределенный интеграл, методы интегрирования 1. Понятия первообразной и неопределенного интеграла. Функция Множество всех первообразных функции 2. Свойства неопределенного интеграла: где k – постоянная, отличная от нуля. 3. Таблица интегралов. 1. 2. 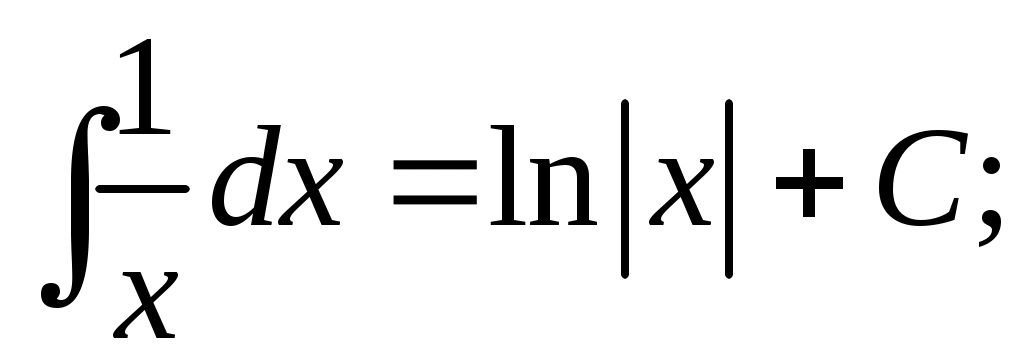 3. 3. 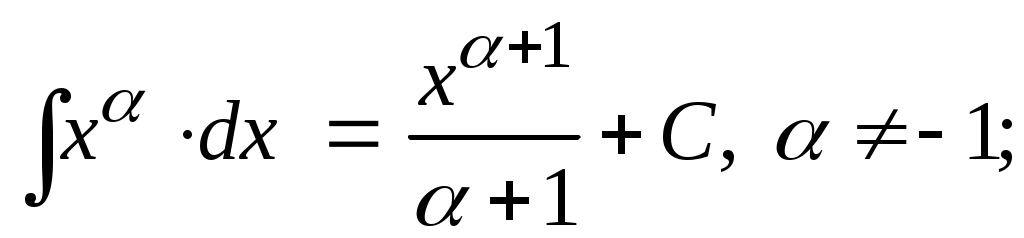 4. 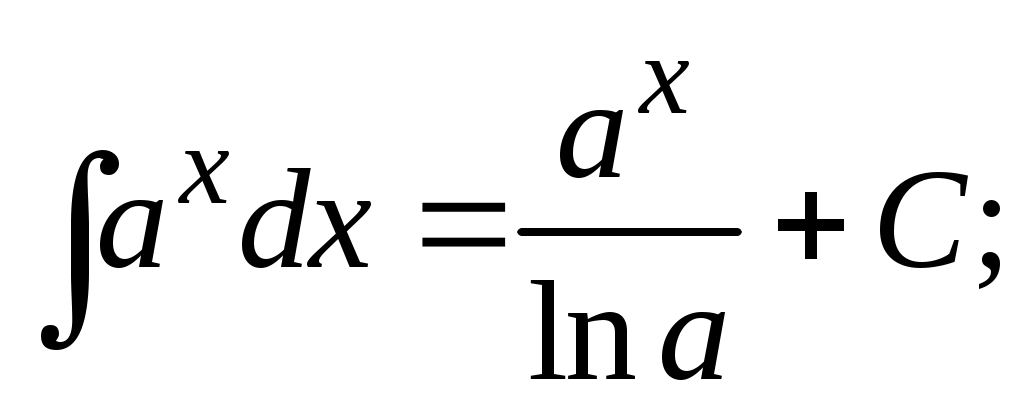 6. 8. 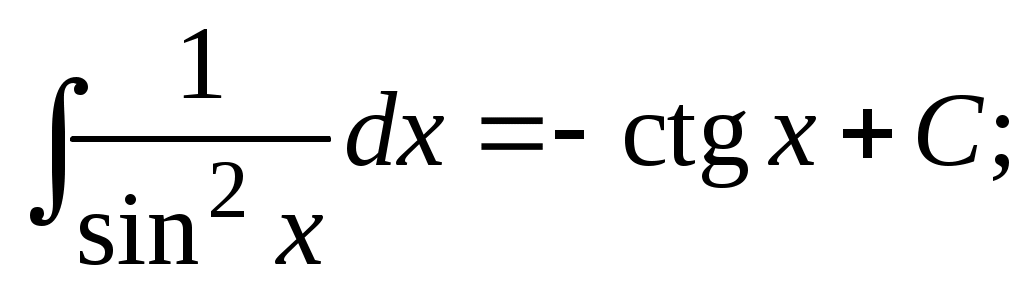 9. 9. 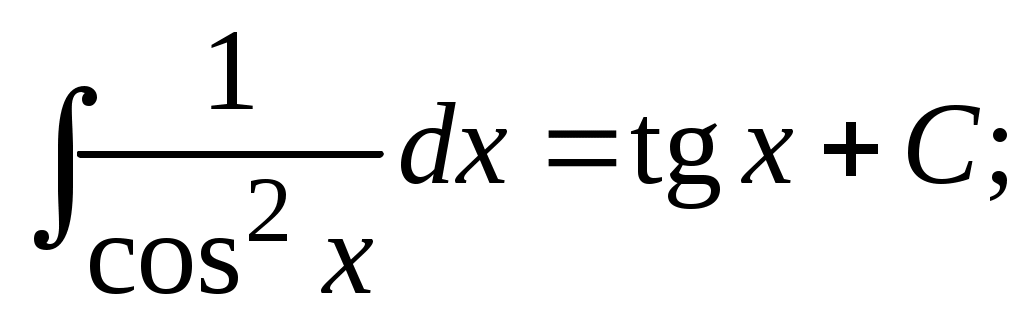 10. 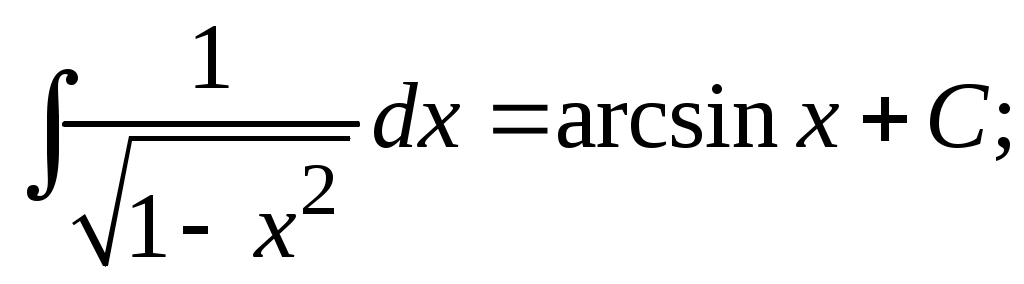 11. 11. 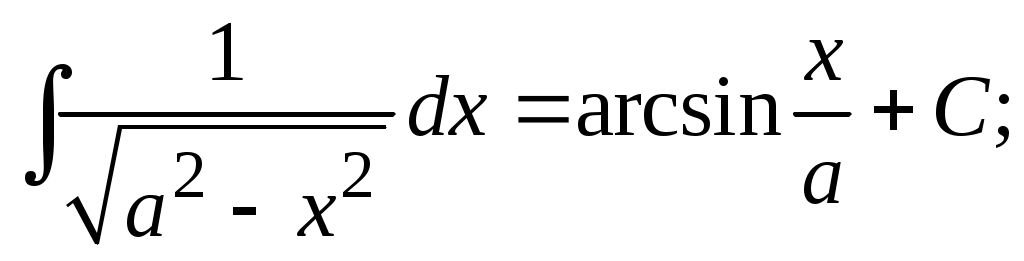 12. 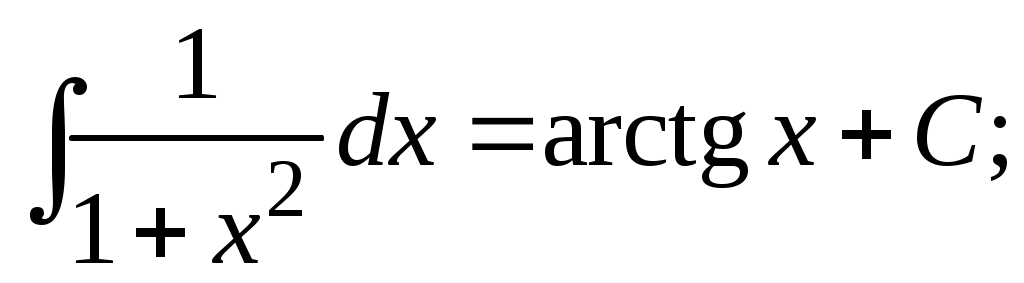 13. 13. 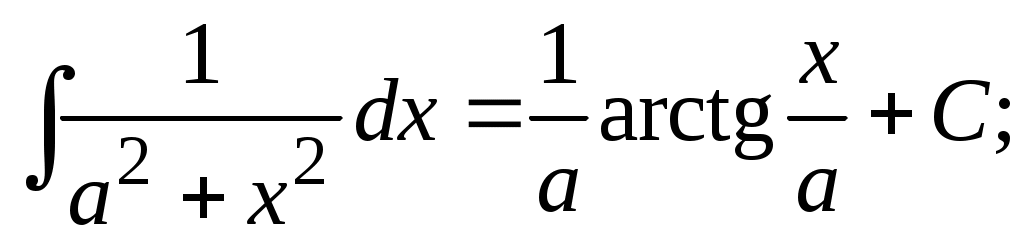 14. 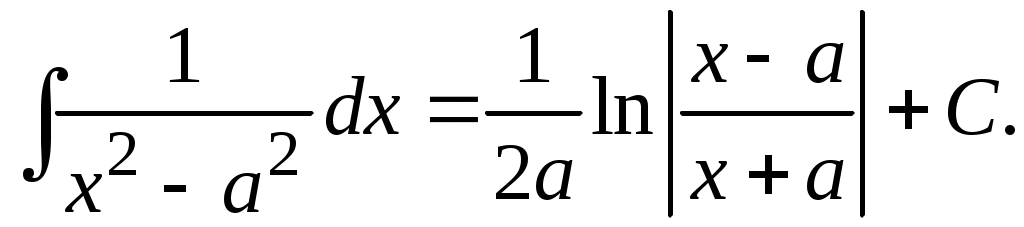 15. 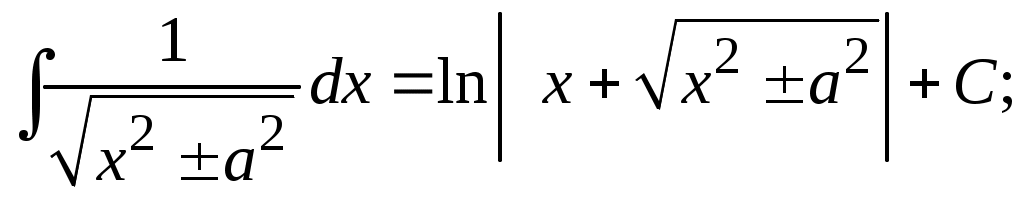 Примечание. Формулы верны, когда переменная х является независимой переменной, а также когда х является функцией другой переменной: х = х(t). 4. Основные методы интегрирования. Идея всех методов интегрирования заключается в приведении искомого интеграла к табличному интегралу или сумме табличных интегралов. 1) Непосредственное интегрирование. Интеграл приводится к табличному виду путем алгебраических или тригонометрических преобразований. 2) Замена переменной (интегрирование подстановкой). Сведение интеграла к табличному виду осуществляется с помощью подстановки t = (x). Тогда дифференциал dt равен Рекомендации по введению новой переменной даны ниже в примерах. 5. Связь между интегрированием и дифференцированием. Интегрирование – это операция, обратная дифференцированию. Если интеграл взят правильно, то производная от интеграла равна подынтегральной функции: 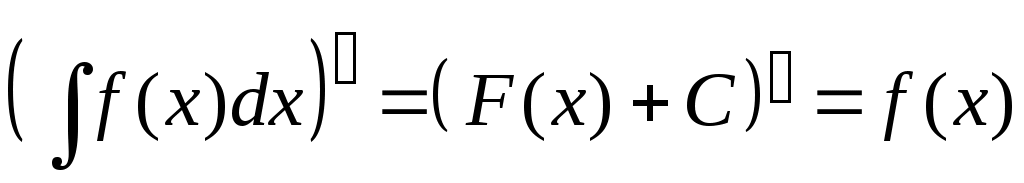 . . Задача.Найти неопределенные интегралы. Результаты проверить дифференцированием. Решение. В контрольной работе интеграл под буквой а берется методом непосредственного интегрирования. При этом используются табличные интегралы от степенных функций: 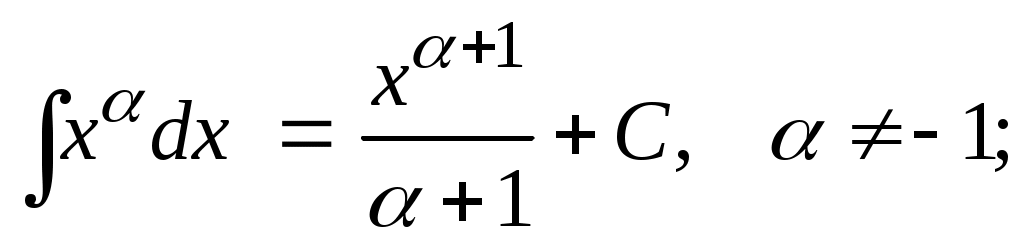 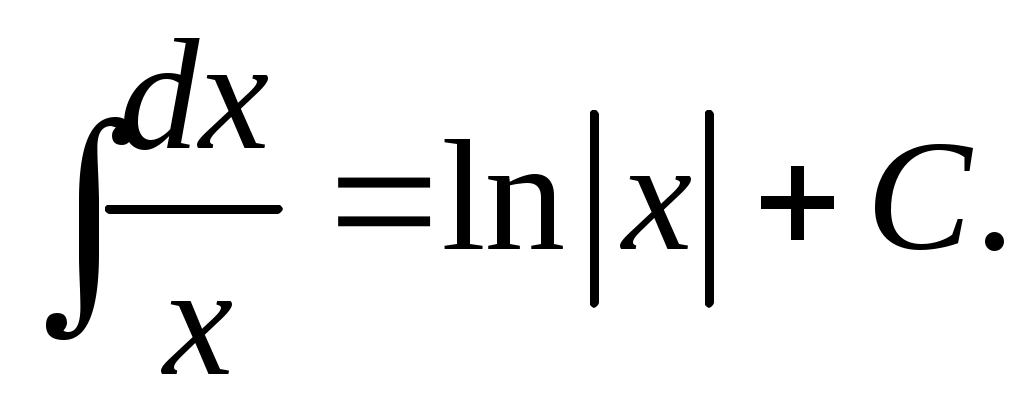 Используются также правила действий со степенями. а) 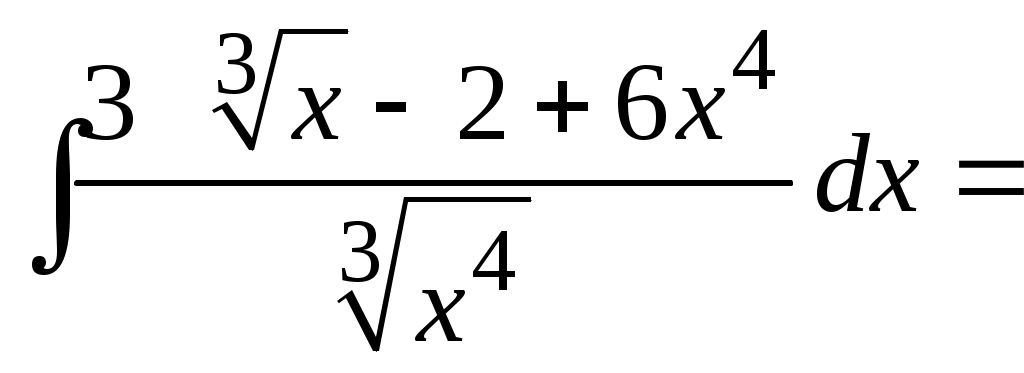 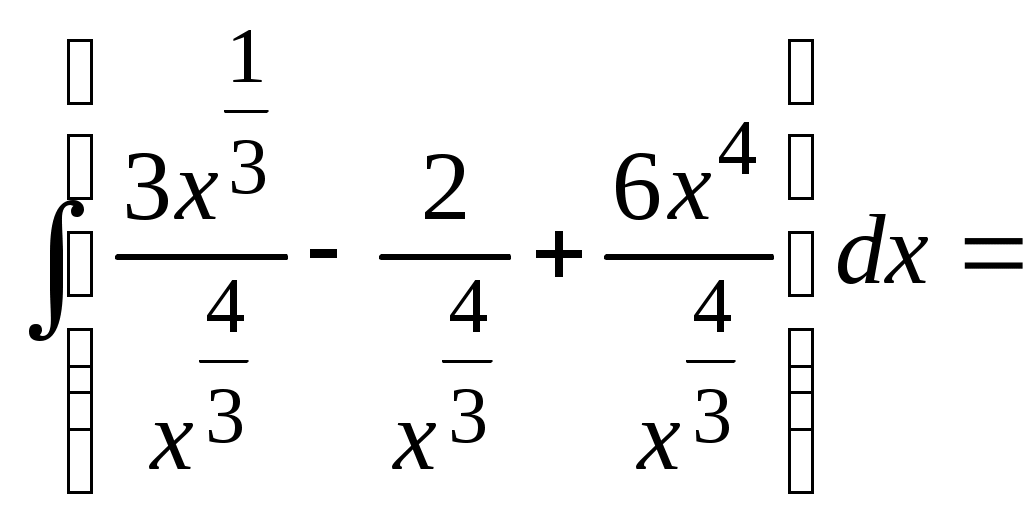 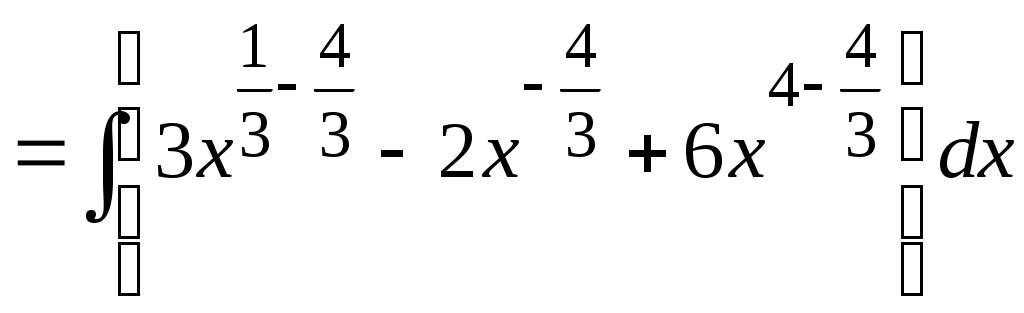 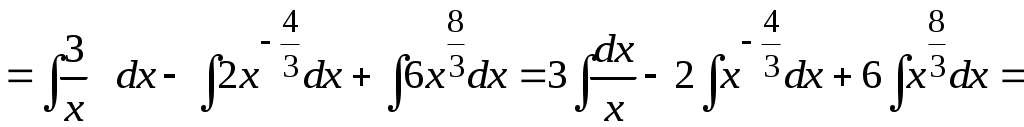 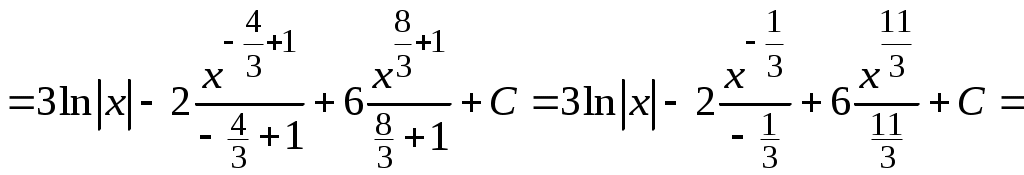 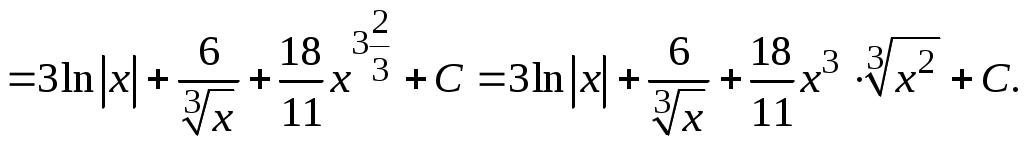 Проверка. 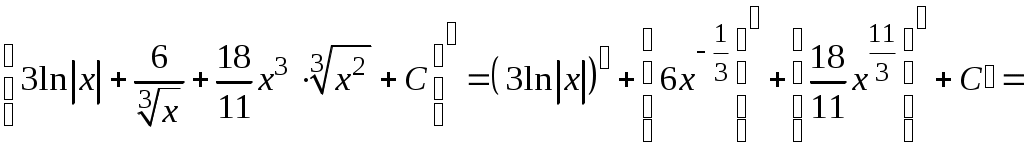 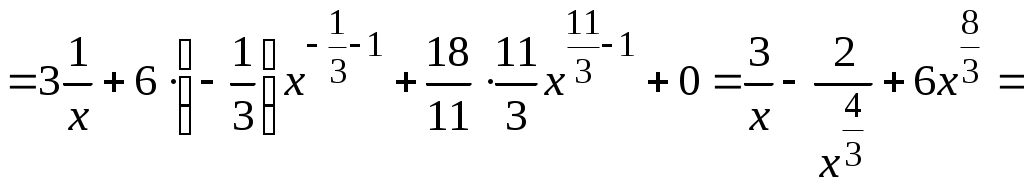 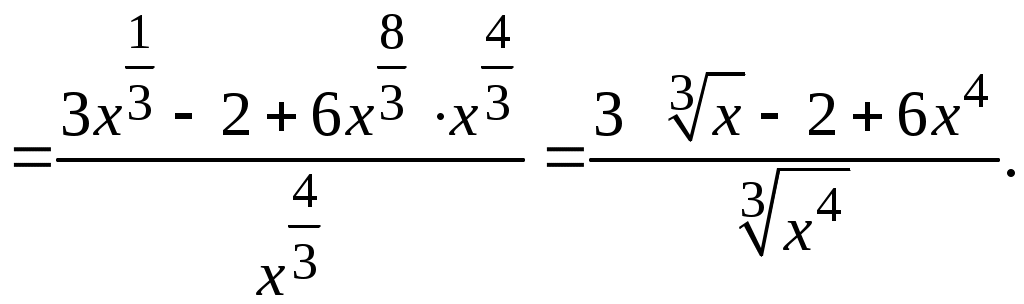 Получена подинтегральная функция, что и требовалось показать. Интеграл б в контрольной работе берется методом замены переменной (подстановкой). Приведем ряд примеров. б.1) 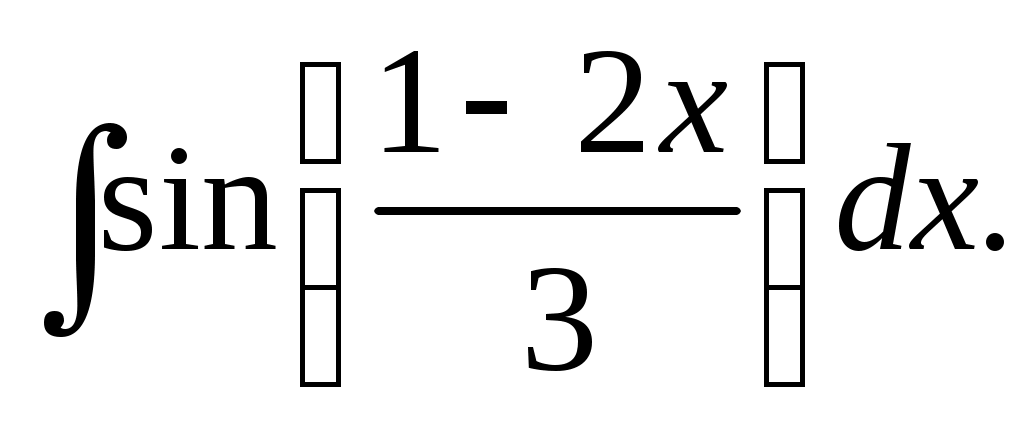 За новую переменную возьмем аргумент подинтегральной функции 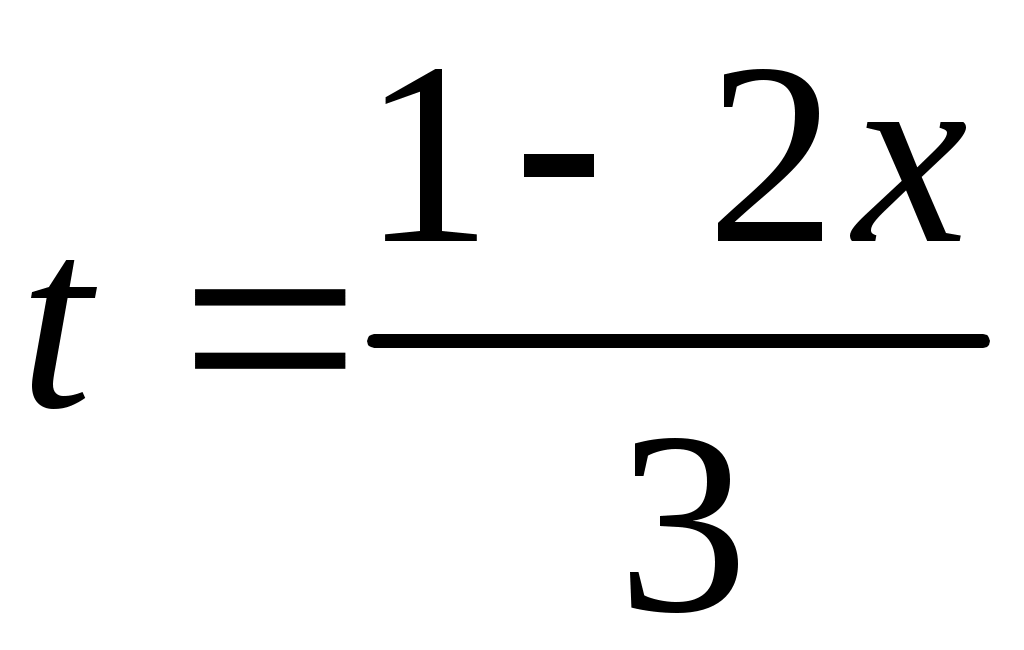 и найдем dtпо формуле: и найдем dtпо формуле: 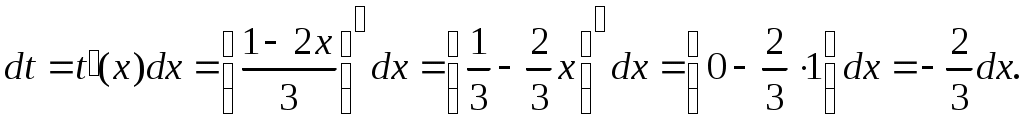 Тогда 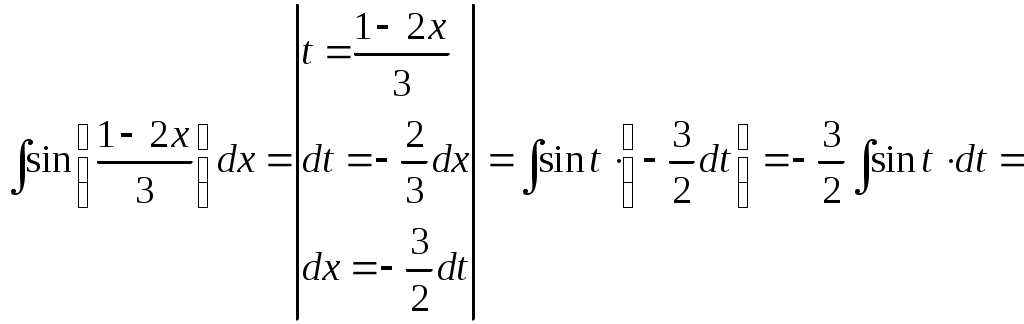 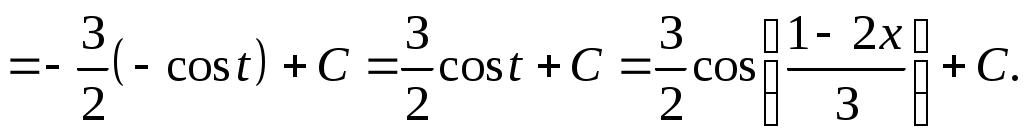 В последнем действии осуществлен переход к исходной переменной x с учетом, что 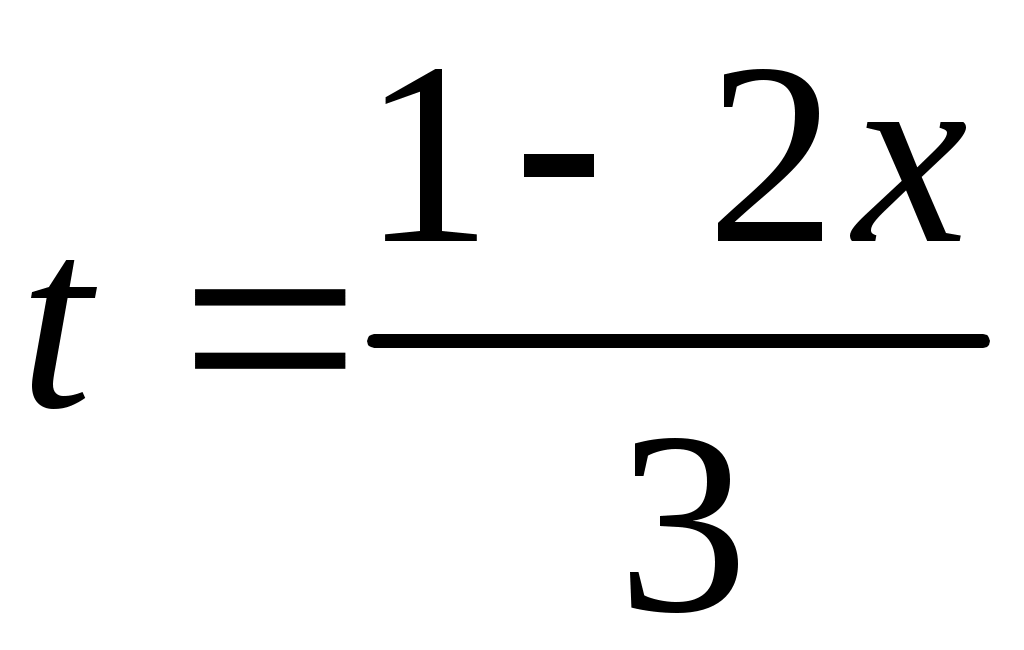 . .Проверка. 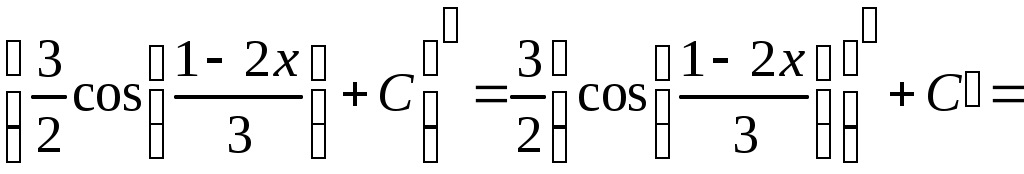 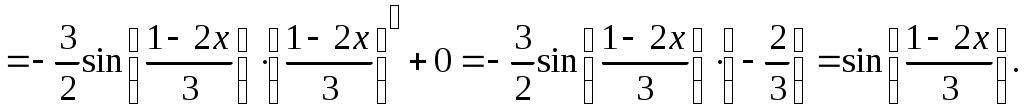 Что и требовалось показать. б.2) 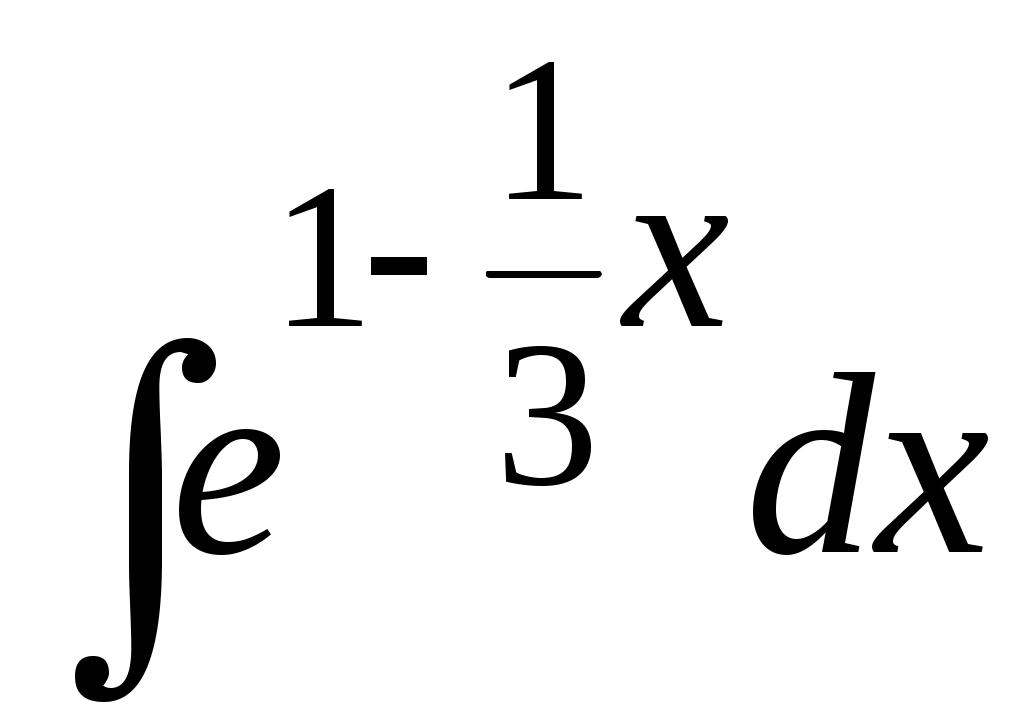 . .За новую переменную возьмем показатель степени 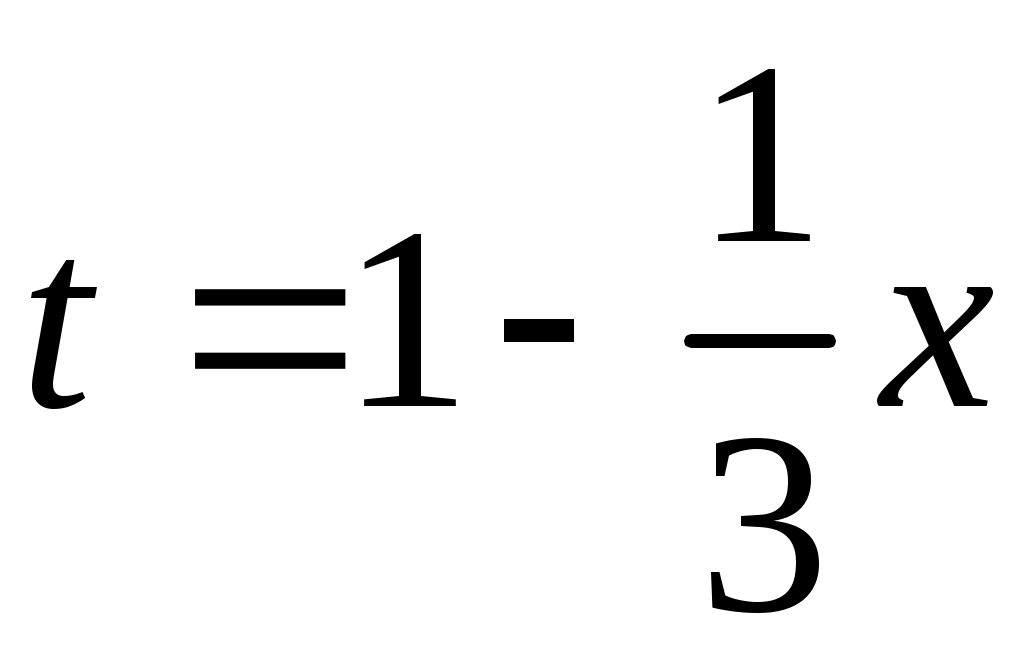 . .Тогда 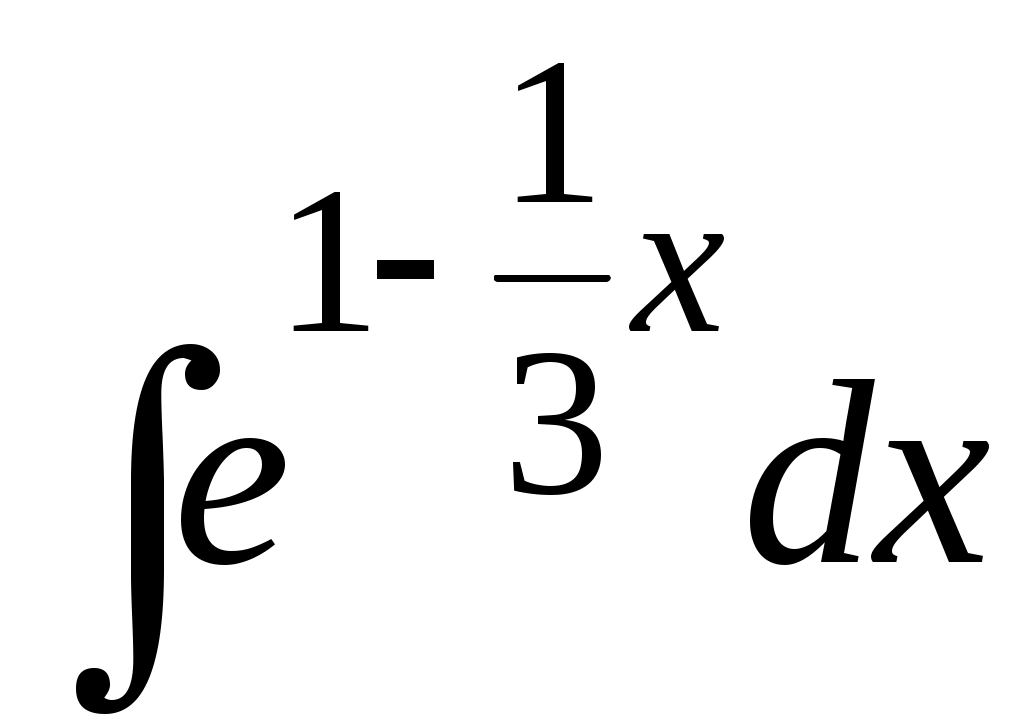 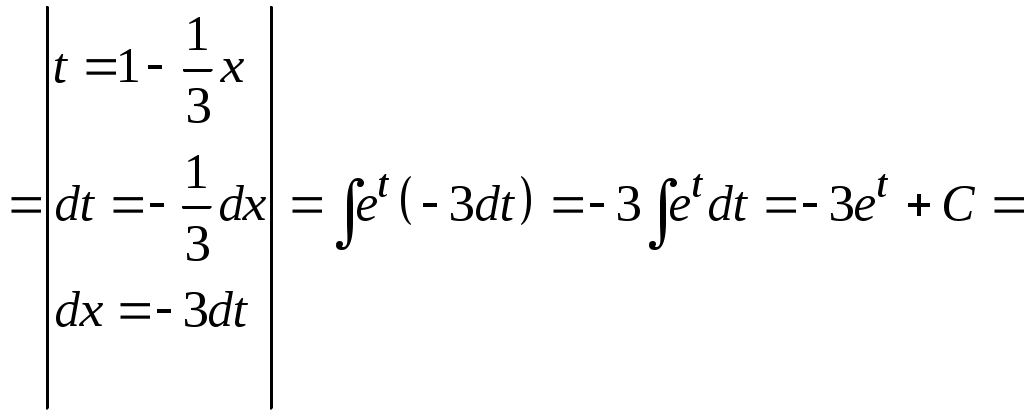 Проверка. 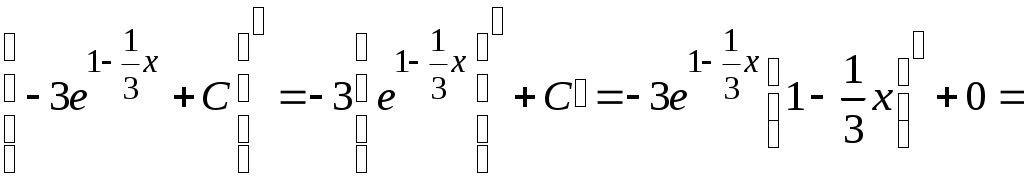 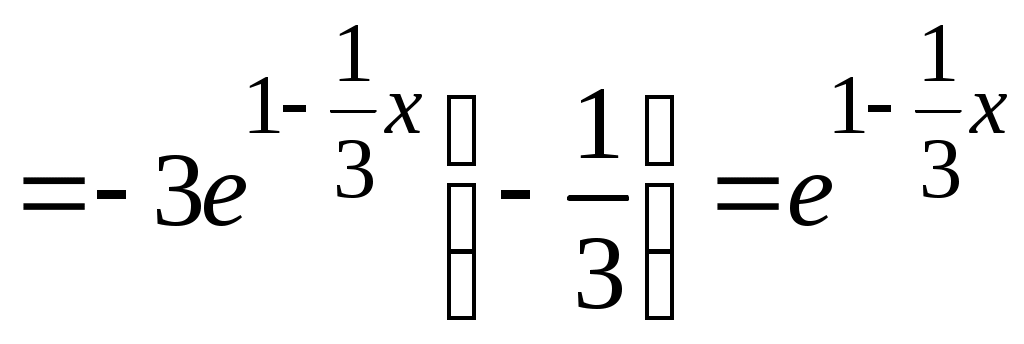 . . Получена подинтегральная функция, что и требовалось показать. б.3) 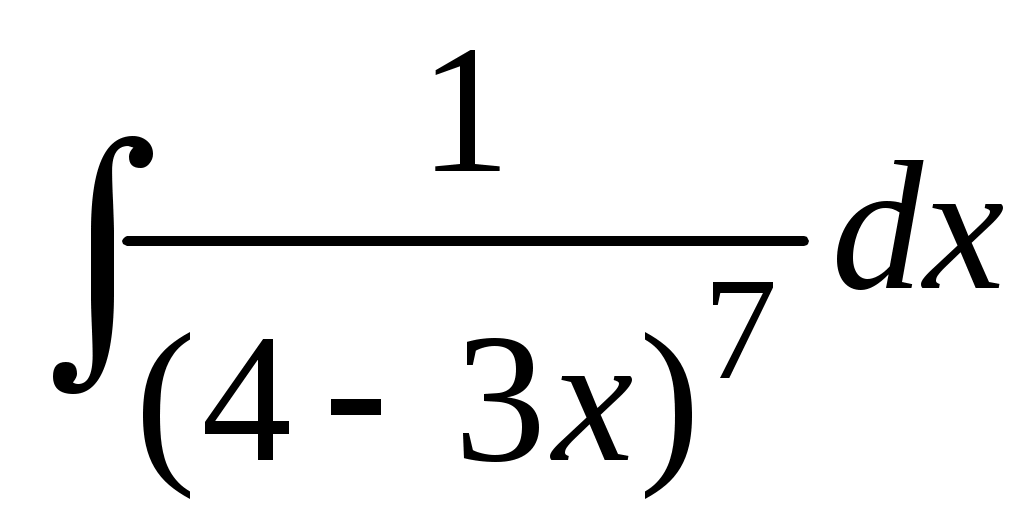 . .За новую переменную возьмем функцию, стоящую в основании степени 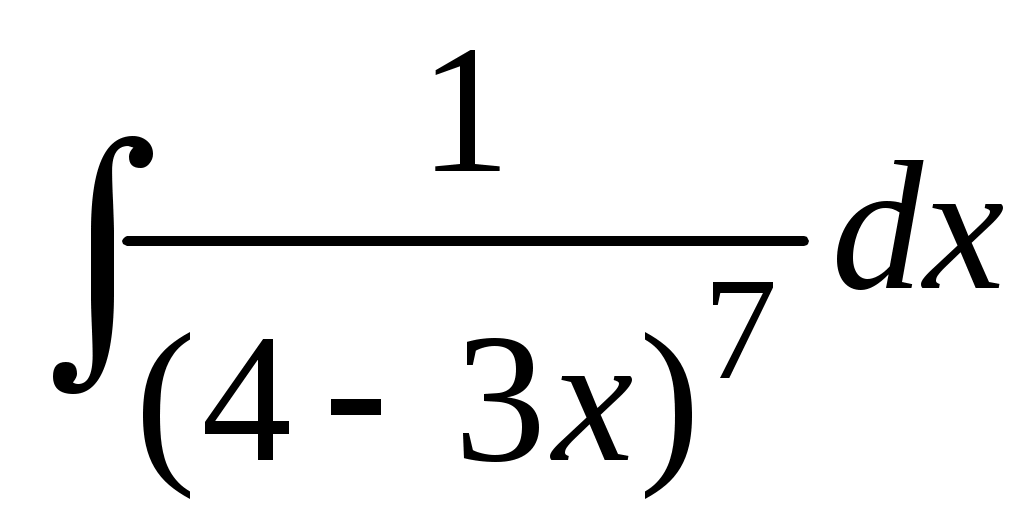 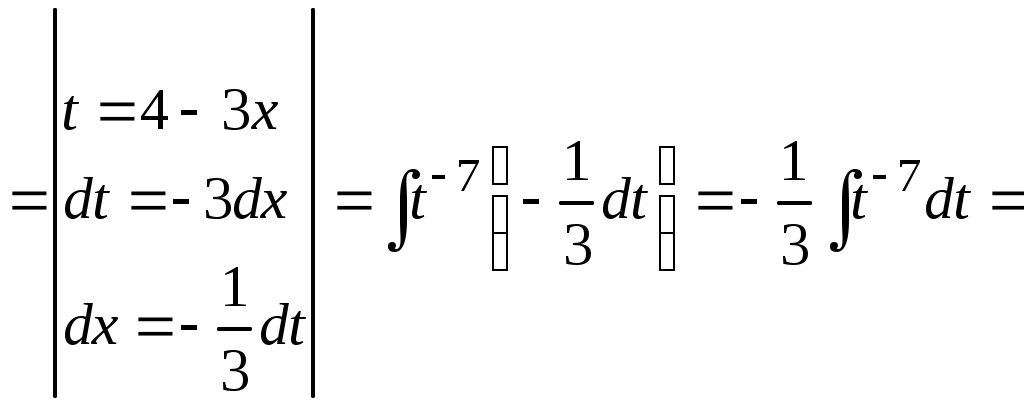 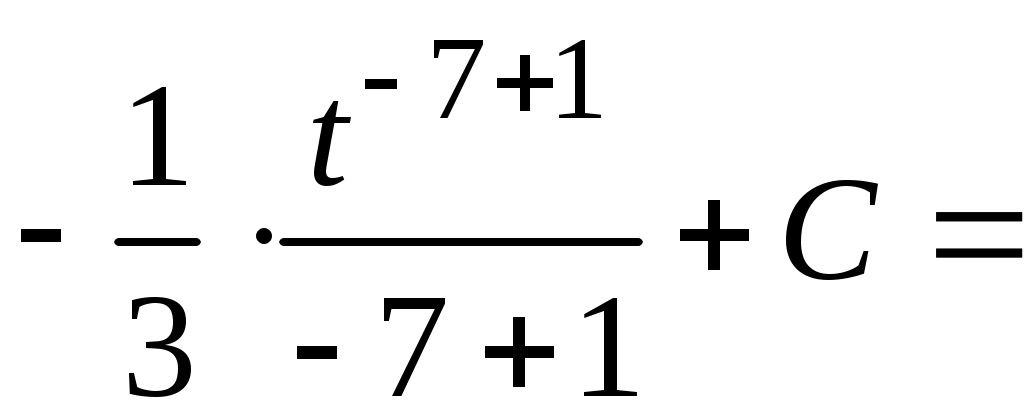 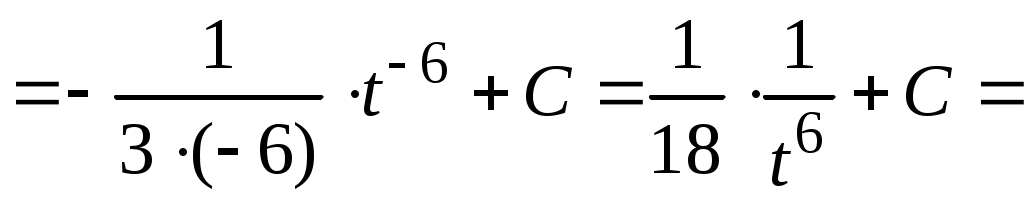 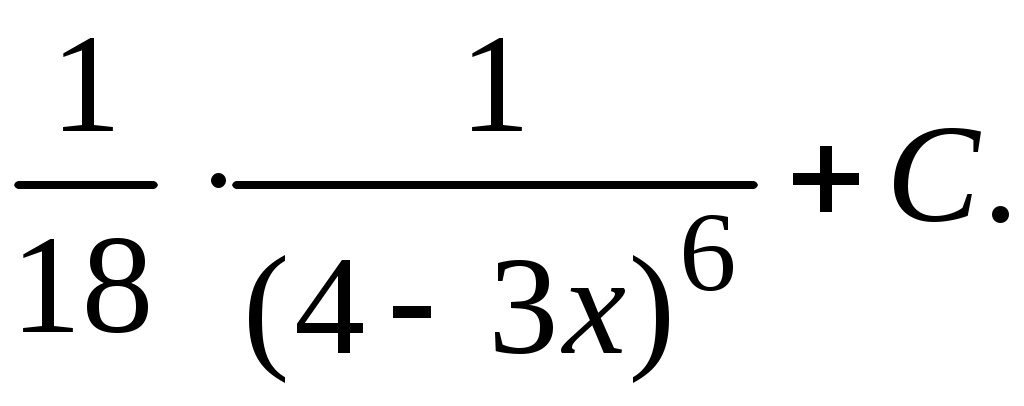 Проверка. 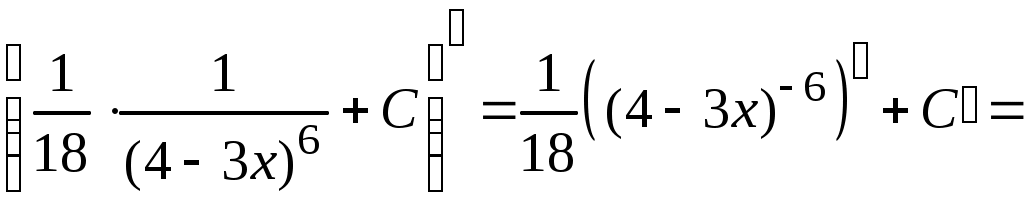 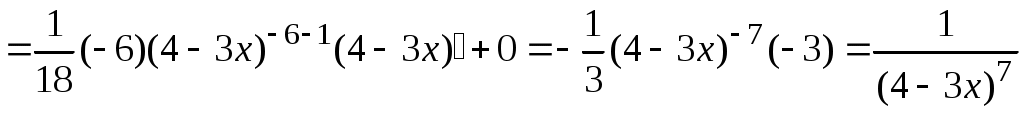 . .Получена подинтегральная функция. Интеграл под буквой в в контрольной работе также берется методом замены переменной (подстановкой). Ознакомимся с примерами таких подстановок. в.1) За новую переменную удобно взять аргумент тригонометриической функции, если к тому же под интегралом присутствует производная этого аргумента в качестве множителя. 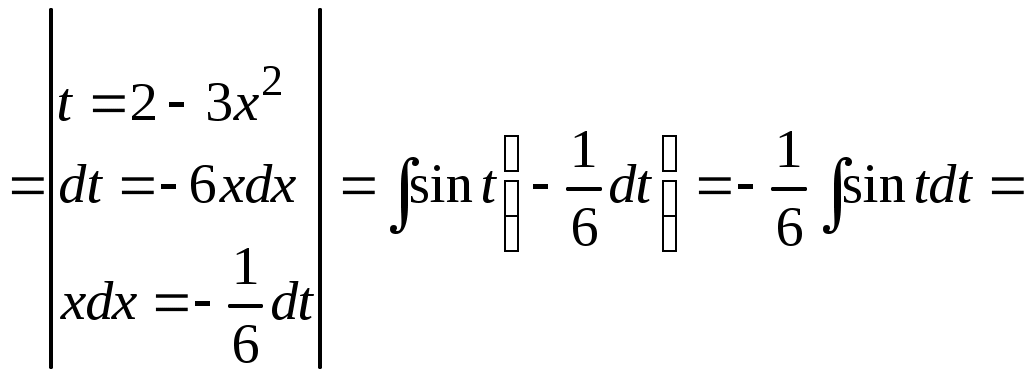 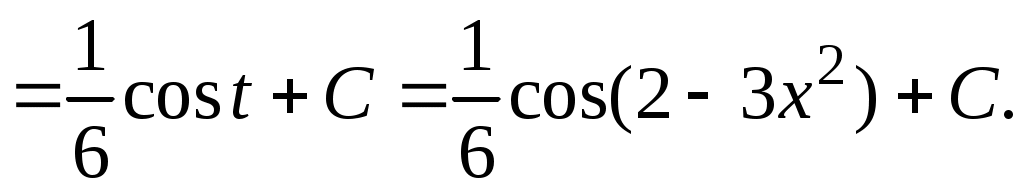 Проверка. 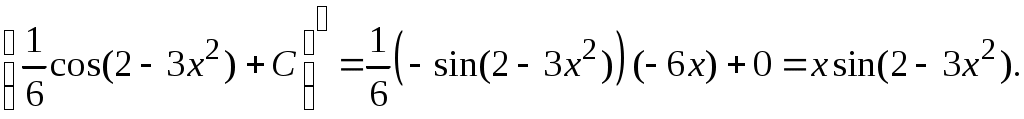 в.2) 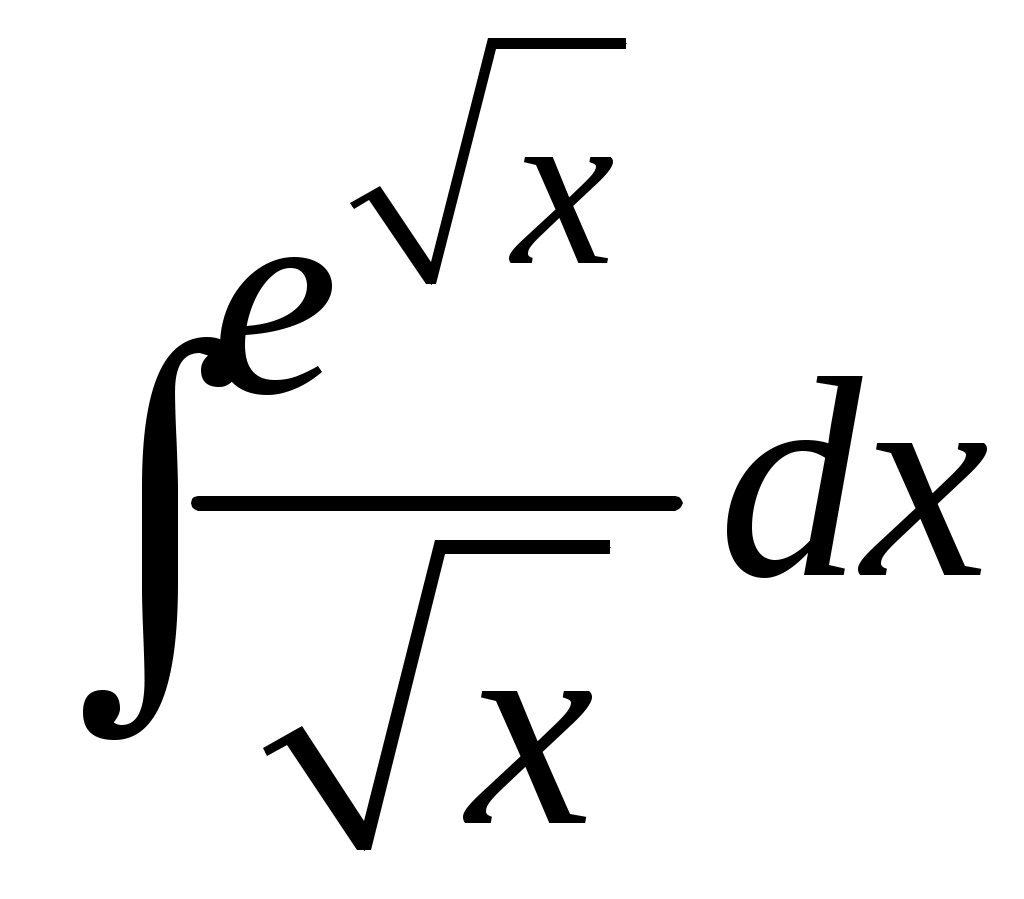 . .Здесь за новую переменную удобно принять показатель степени, учитывая, что под знаком интеграла присутствует производная этого показателя (с точностью до постоянного множителя). 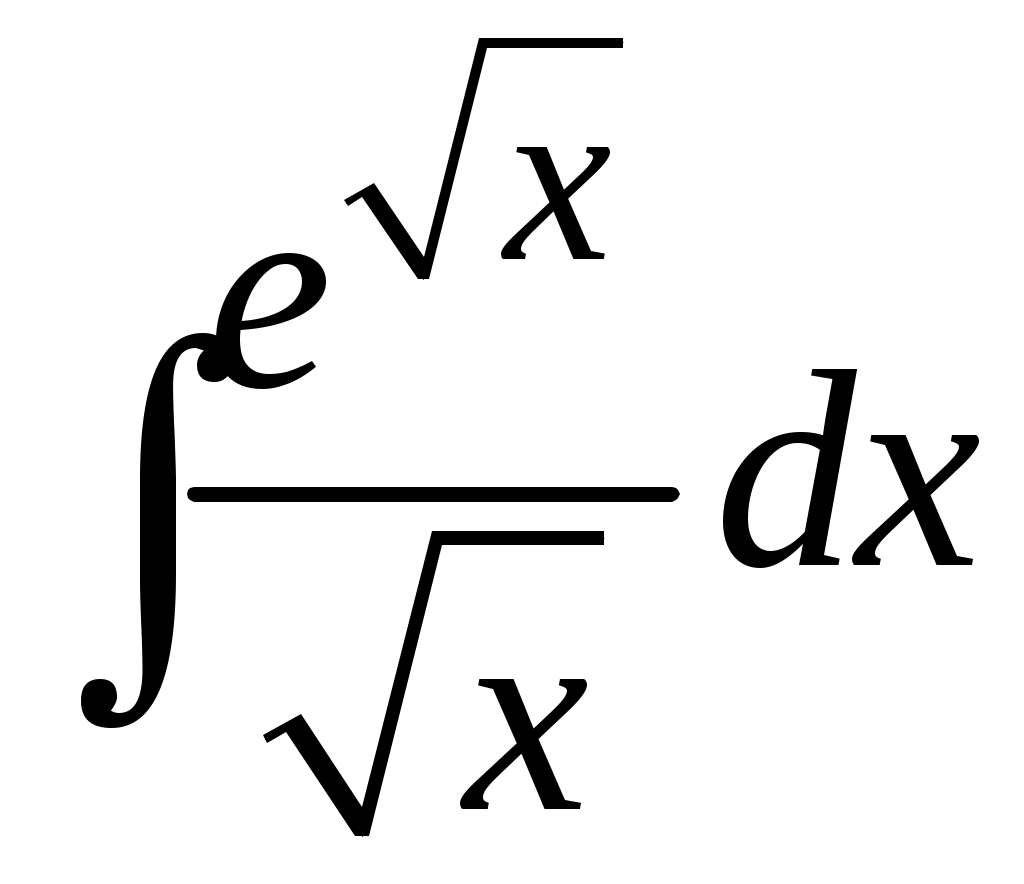 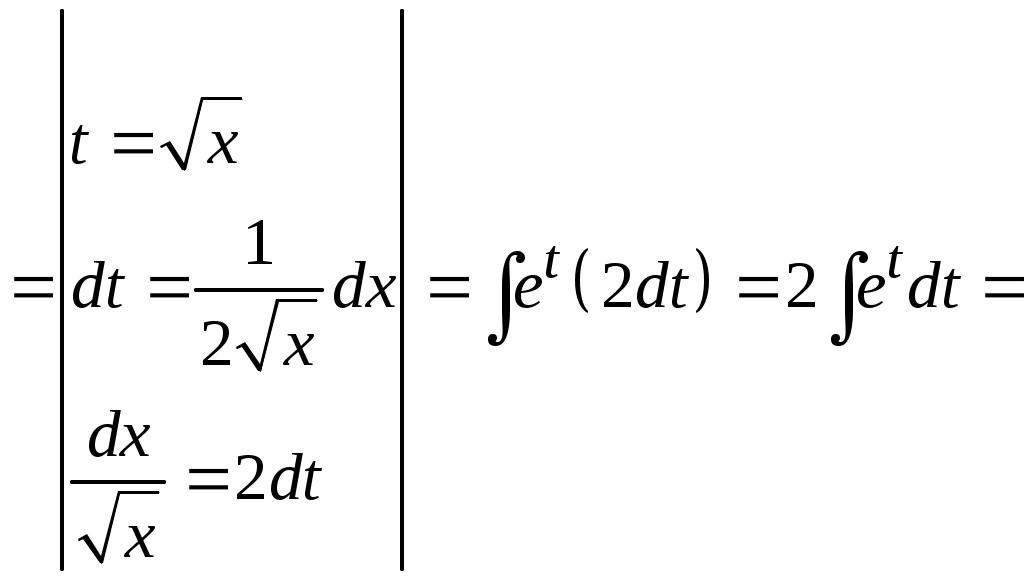 Проверка. 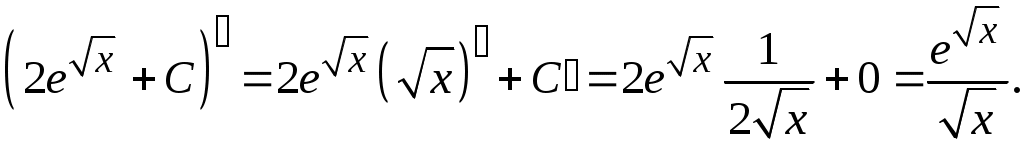 в.3) За новую переменную удобно взять подкоренное выражение, так как под интегралом присутствует также его производная (с точностью до постоянного множителя). 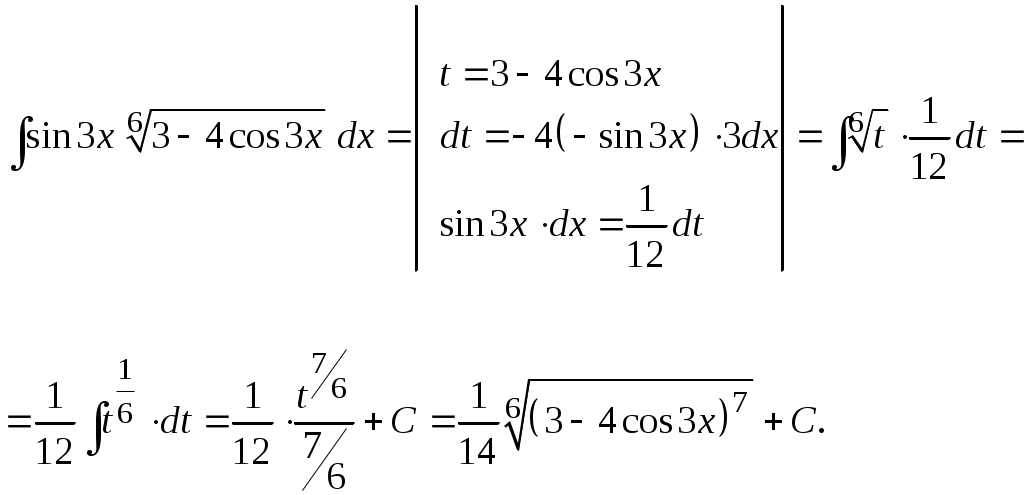 Проверка. 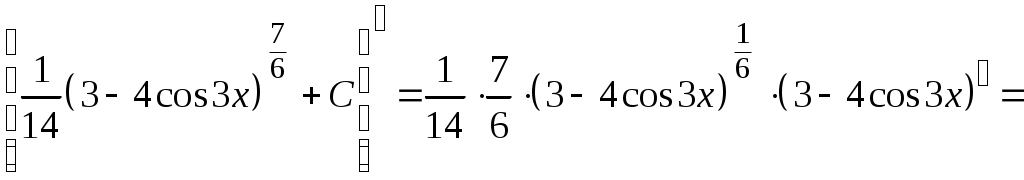 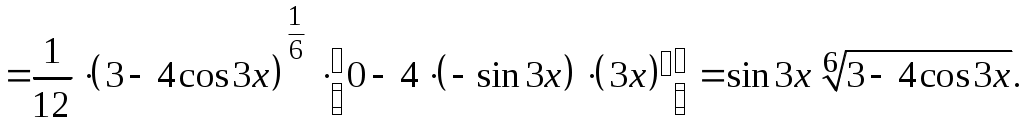 Получена подинтегральная функция, что и требовалось показать. в.4) 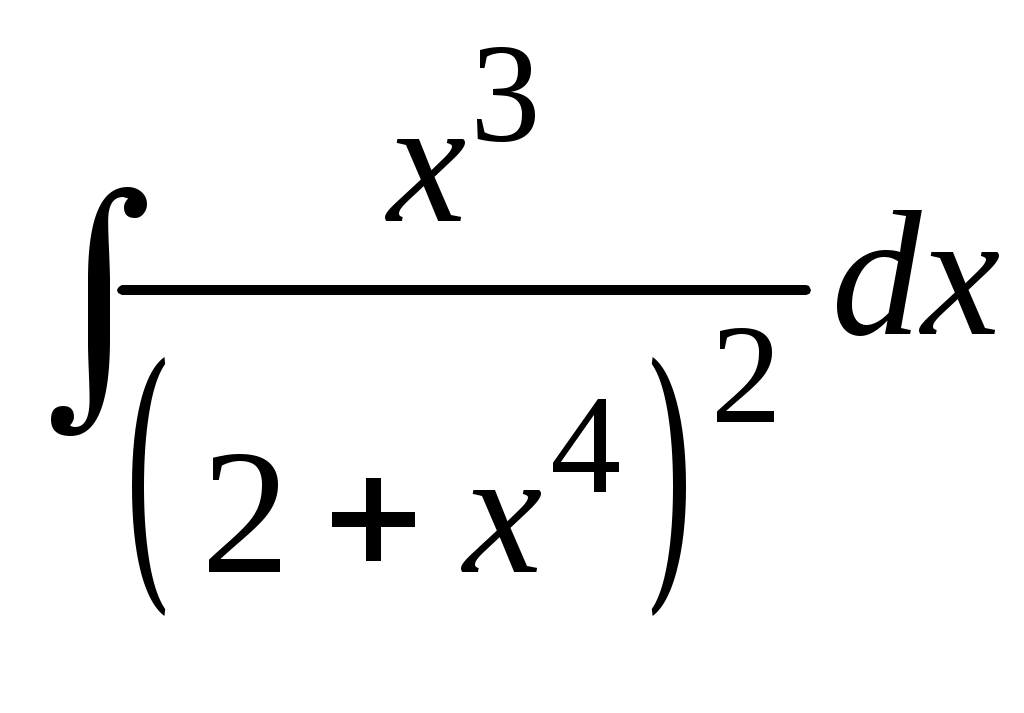 . .За новую переменную берем функцию, стоящую в основании степени, так как подынтегральное выражение содержит производную этой функции (с точностью до постоянного множителя). 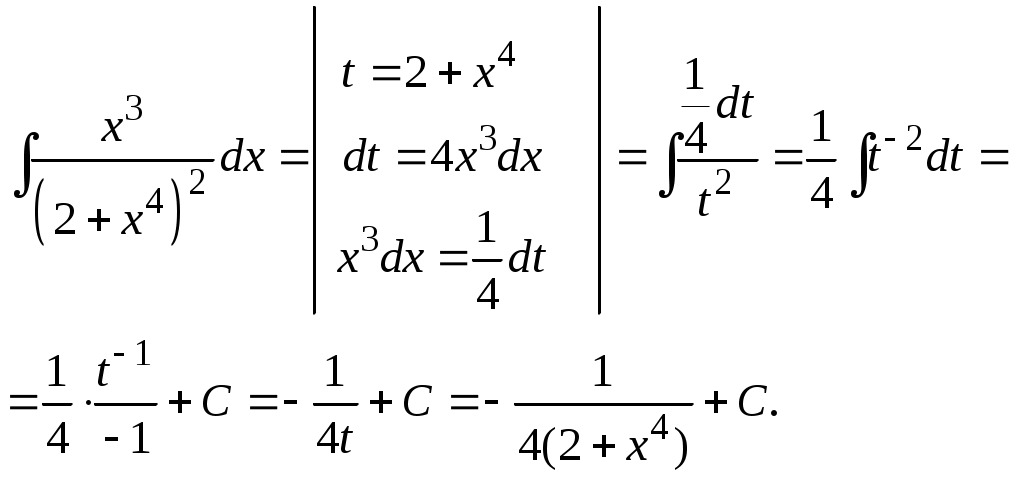 Проверка. 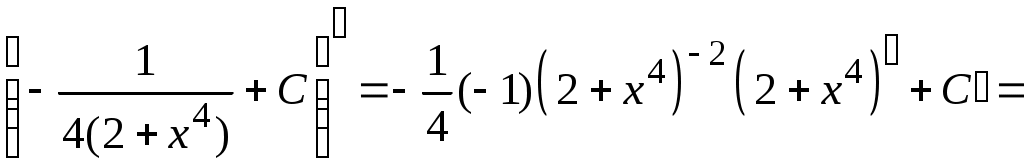 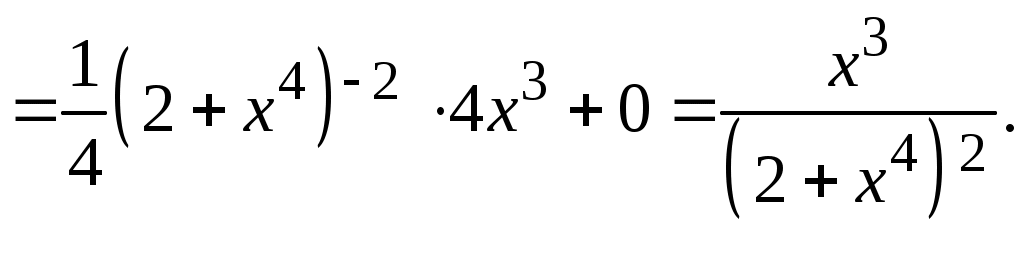 Задачи 51–60 Вычислить площадь фигуры, ограниченную заданными линиями. Сделать чертеж.
Методические указания к решению задач 51 – 60 Определенный интеграл, вычисление площадей Понятие определенного интеграла. Определенный интеграл является числом, которое находится по формуле Ньютона-Лейбница: 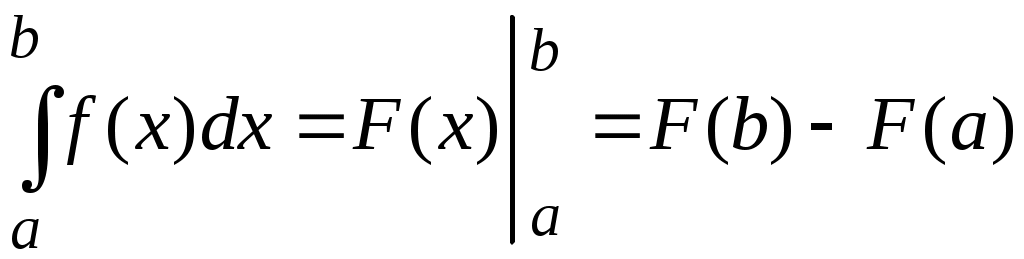 , ,где Формула Ньютона-Лейбница связывает определенный и неопределенный интегралы. Чтобы ею воспользоваться, следует взять сначала неопределенный интеграл, то есть найти первообразную, причем удобно взять произвольную постоянную равной нулю: Например: 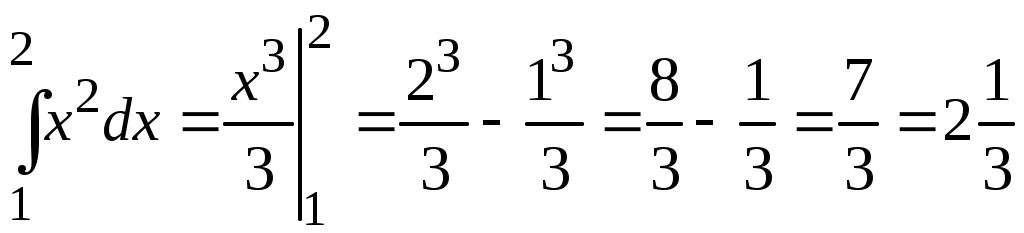 . .Геометрический смысл определенного интеграла. Если функция 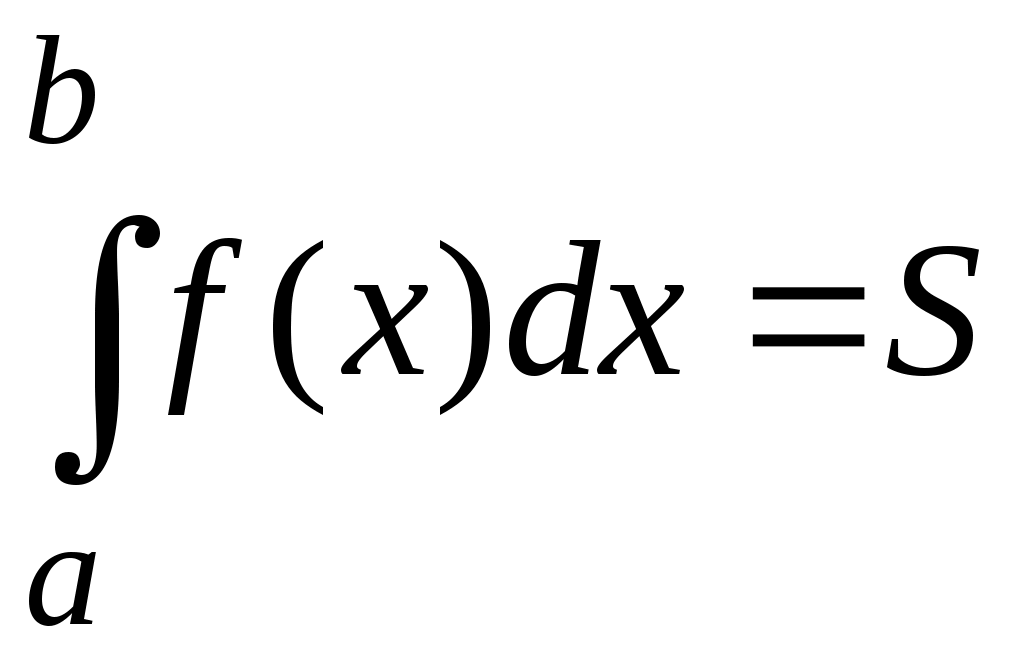 , ,где S– площадь под кривой 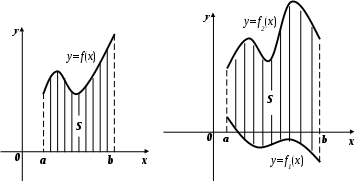 Рис. 6 Рис. 7 Вычисление площадей плоских фигур. Площадь фигуры, заключенной между кривыми 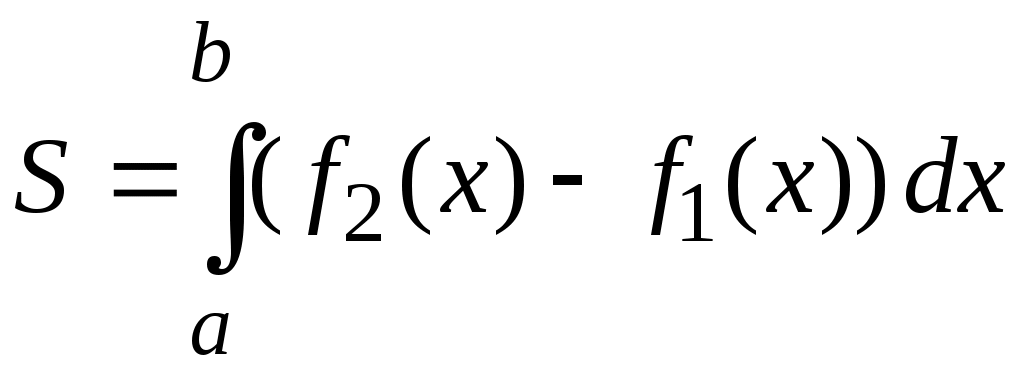 , ,при этом Задача.Вычислить площадь фигуры, ограниченной линиями Решение. Выполним чертеж. Первое уравнение определяет параболу, а второе – прямую линию. Для построения параболы найдем координаты её вершины и точки пересечения её с осями координат. Если уравнение параболы 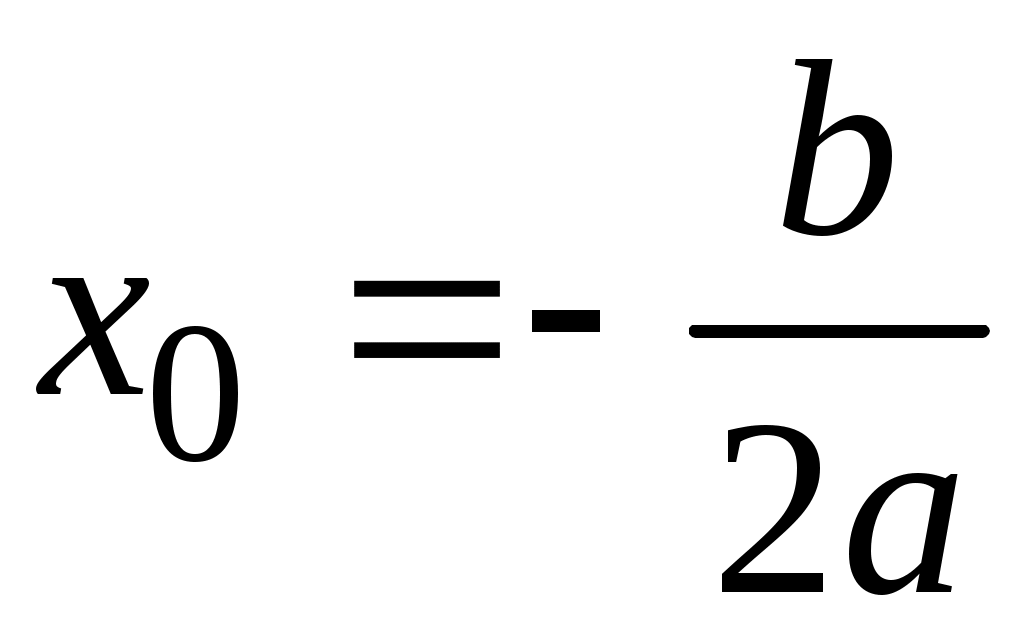 . В данной задаче . В данной задаче 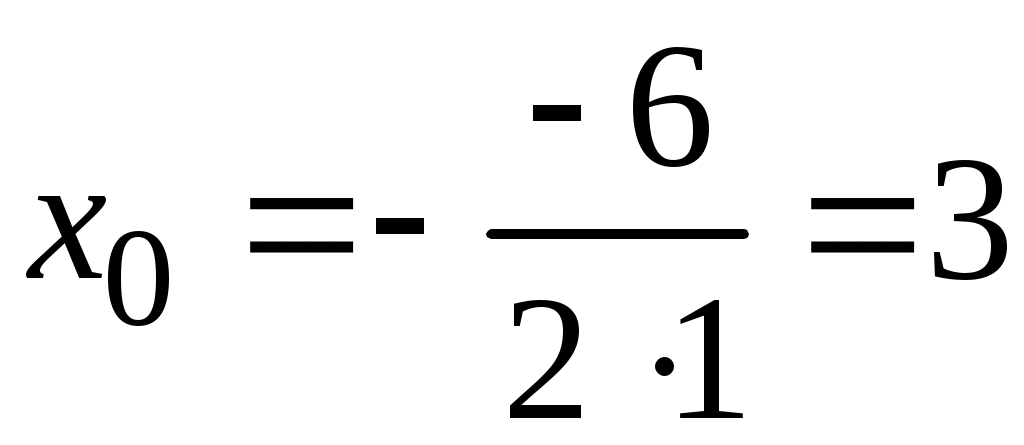 , , Найдем точки пересечения параболы с осями координат. С осью Ox: С осью Oy: Строим параболу по найденным точкам, замечая, что ветви параболы направлены вверх, так как Прямую при Получены точки: Найдем точки пересечения параболы и прямой, решив систему уравнений: 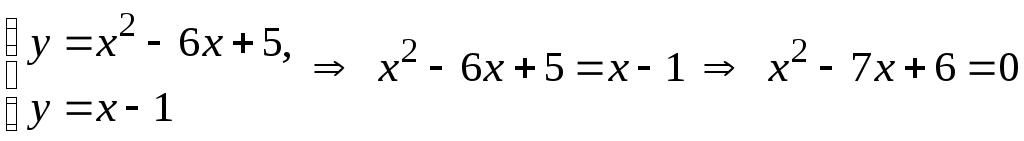 . .Решим полученное квадратное уравнение: 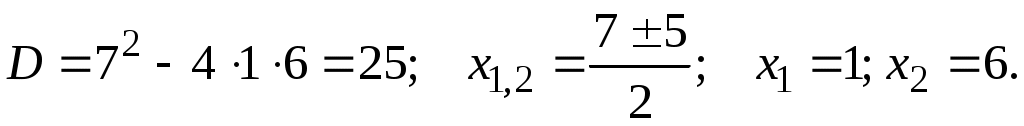 Найдем соответствующие ординаты прямой это точки 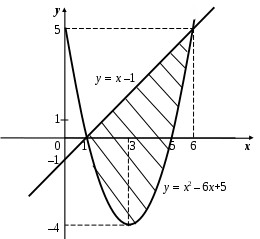 Рис. 8 Заштрихуем плоскую фигуру, ограниченную параболой и прямой (рис.8). Здесь функции Для нахождения искомой площади воспользуемся формулой 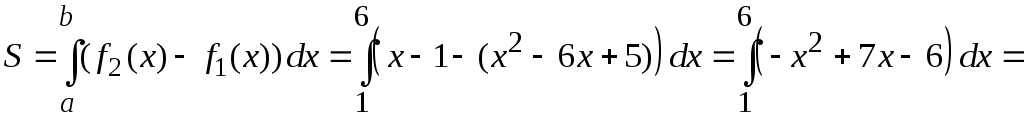 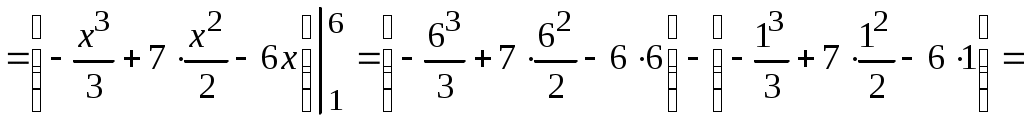 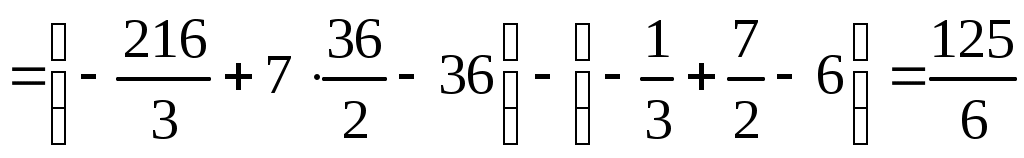 . .Ответ. Искомая площадь равна: 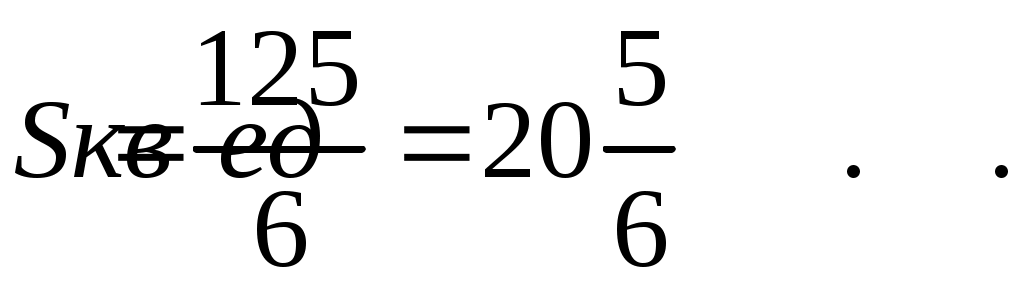 Замечание. Если одна из линий – гипербола, например, xy = –6, то ее можно построить по точкам. Удобно взять точки с абсциссами 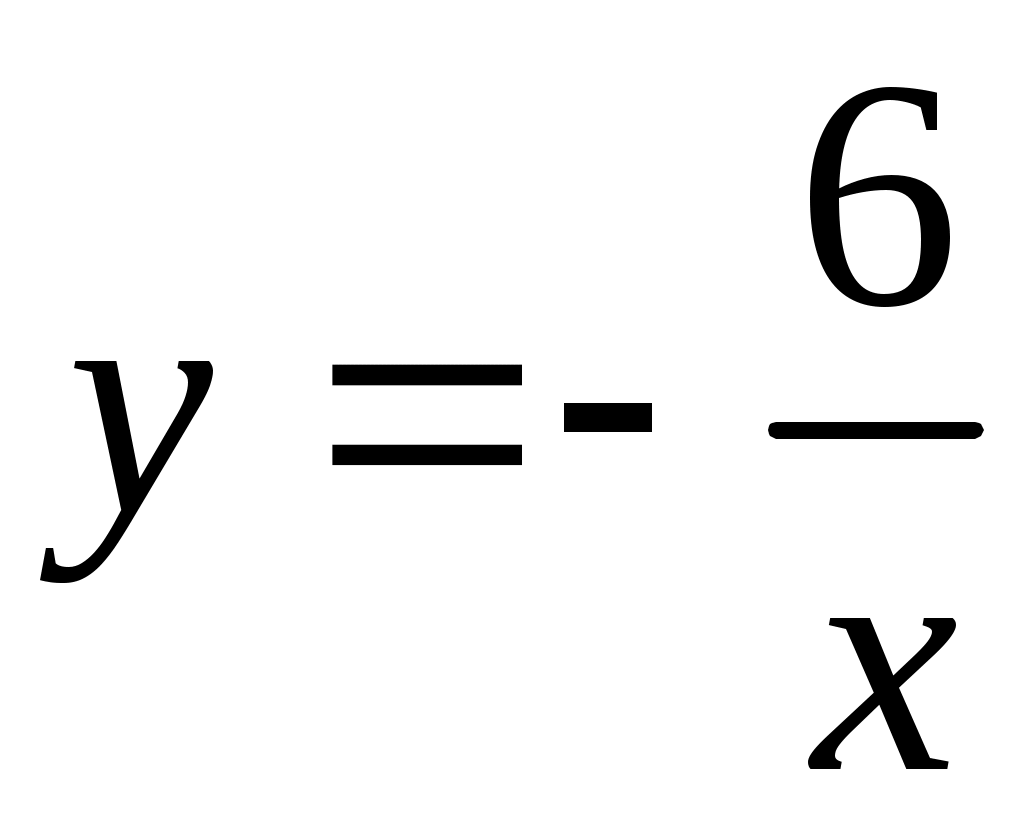 . .Теория вероятностей Задачи 61–70 Партия мужских костюмов состоит из kкостюмовпроизводителя «А» и mкостюмов производителя «В». Некто наугад выбирает из партии один за другим два костюма. Найти вероятность того, что а) оба костюма изготовлены производителем «А»; б) выбраны костюмы разных производителей; в) хотя бы один из них изготовлен производителем «А». Найти вероятности указанных событий, если костюмы выбираются по схеме выборки: 1) с возвращением; 2) без возвращения.
Методические указания к решению задач 61-70 Основные понятия теории вероятностей Испытание – это изначальное понятие, разъясняется как действие, наблюдение, опыт и прочее. Событие – это результат испытания. Пример 1: Некто подбросил монету, которая упала гербом вверх. Здесь испытание – подбрасывание монеты, а результат этого испытания – выпадение герба – это событие. Пример 2: В результате подбрасывания игрального кубика выпало три очка на верхней грани. В этом случае, испытание – подбрасывание кубика, а выпадение трех очков – событие. Заметим, что монета в примере 1 могла упасть не гербом, а решкой (цифрой вверх). Аналогично, в примере 2, подбрасывание кубика могло бы закончиться выпадением, например, двух или пяти очков. Событие, которое в результате испытания может произойти, а может и не произойти, называется случайным. Пусть в результате испытания могут появиться несколько событий. События называются несовместными, если появление одного из них исключает появление других. Пример 3: Рассмотрим такое испытание, как сдача экзамена по математике одним из студентов. События, которые, например, могут произойти в результате этого испытания, есть следующие: А – экзамен сдан на оценку «4», В – экзамен сдан на оценку «3», С – экзамен сдан на оценку выше, чем «3». В этом случае, события А и В несовместны, так как получение оценки «3» делает невозможным получение оценки «4» за этот же экзамен. Наоборот, события А и С совместны, поскольку они могут произойти одновременно. Пространством элементарных исходов (или событий), соответствующих рассматриваемому испытанию, будем называть такое множество несовместных событий, одно из которых обязательно произойдет в результате испытания, так что любой интересующий нас результат испытания может быть однозначно описан с помощью элементов этого множества. В примере с игральным кубиком пространство элементарных исходов образуют 6 событий: E1,E2, E3, E4, E5, E6, которые заключаются в том, что количество выпавших очков составит соответственно 1, 2, 3, 4, 5 или 6 очков. Действительно, эти события несовместны, одно из них обязательно произойдет в результате подбрасывания кубика, и с их помощью можно описать любые другие события. Например, событие A– выпало четное число очков – означает, что появились события E2 или E4 или E6, эти три элементарных исхода благоприятствуют наступлению события A. Классическое определение вероятности Элементарные исходы называются равновозможными, если ни у одного из них нет преимуществ перед другими, чтобы произойти в результате испытания. Вероятностью события Aназывается число P(A), равное отношению числа mблагоприятствующих событию Aэлементарных исходов к общему числу nэлементарных равновозможных исходов: Рассмотрим пример с урновой схемой. Урна – это ёмкость с шарами. Пример 4: Пусть в урне находится 20 одинаковых шаров, которые отличаются только цветом, например, 12 из них красные, а остальные – белые. Некто подошел к урне и наугад выбрал один шар. Найдем вероятность того, что этот шар – красный. Пусть событие К – выбран красный шар. Всего элементарных исходов n = 20 (по количеству шаров), причём все эти исходы равновозможные. Событию К благоприятствует m = 12 исходов (по количеству красных шаров), поэтому |
