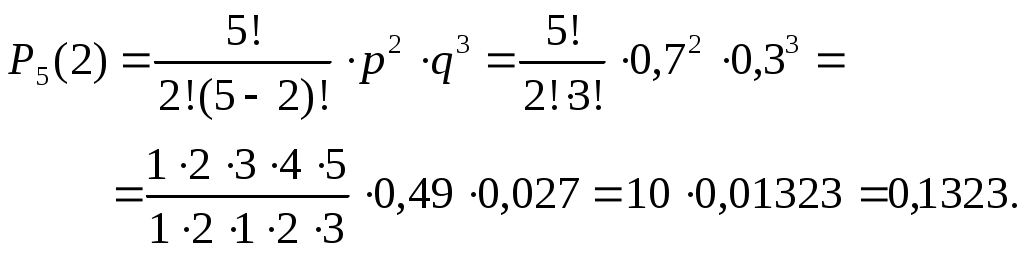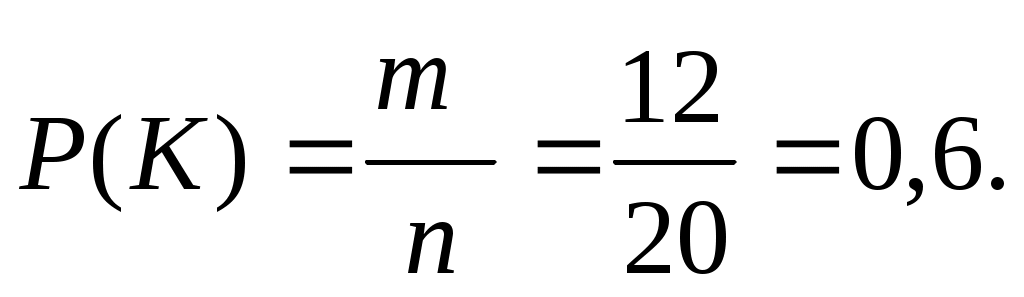
Вероятность любого события может принимать значения только от 0 до 1 включительно, то есть
 . .
Достоверное событие – обязательно произойдет в результате испытания, то естьm = n, так как все исходы благоприятные:
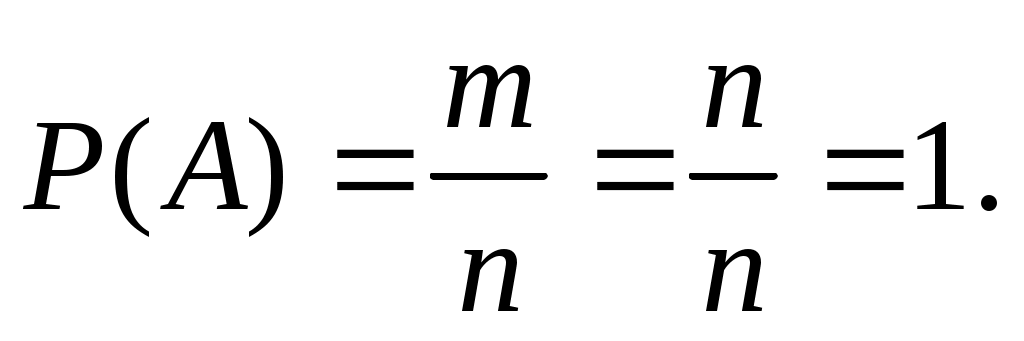
Невозможное событие – не может произойти в результате испытания, то есть m= 0, так как благоприятных исходов нет:
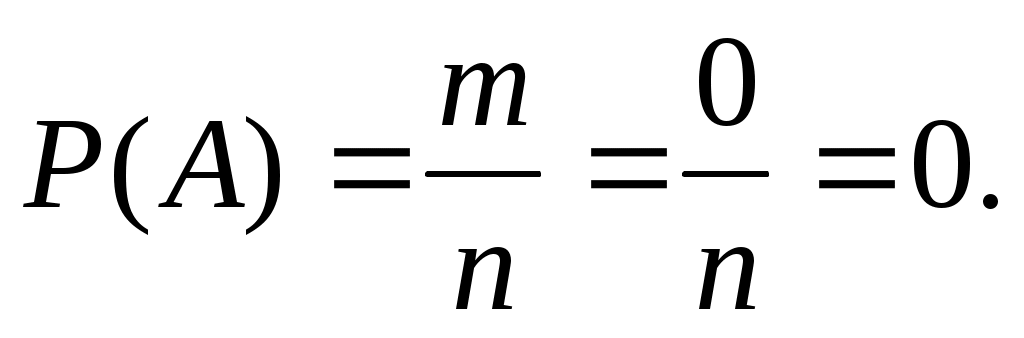
Случайное событие – может произойти или не произойти в результате испытания: 0<P(A)<1.
Вероятность является числовой мерой объективной возможности наступления события. Вероятность можно задать в процентах, например P(A)= 0,8 (80%).
Основные теоремы теории вероятностей
Условной вероятностью РА(В) называется вероятность события В, вычисленная в предположении, что событие А уже наступило.
Пример 5. В урне имеется 3 белых и 2 черных шара. Из урны дважды вынимают по одному шару, не возвращая их обратно. Найти вероятность появления белого шара при втором испытании (событие В), если при первом испытании был извлечен черный шар (событие А).
Решение: Изначально в урне было 5 шаров, из которых 3белых и 2 черных. После первого испытания в урне осталось 4 шара, из них 3 белых. Искомая условная вероятность РА ( В )= 3/4.
События А и В называются независимыми, если появление одного из этих событий не изменяет вероятности наступления другого, то есть Р( А )= РВ ( А ) или Р( В )=РА( В ). В противном случае события называются зависимыми.
Теорема сложения вероятностей несовместных событий:
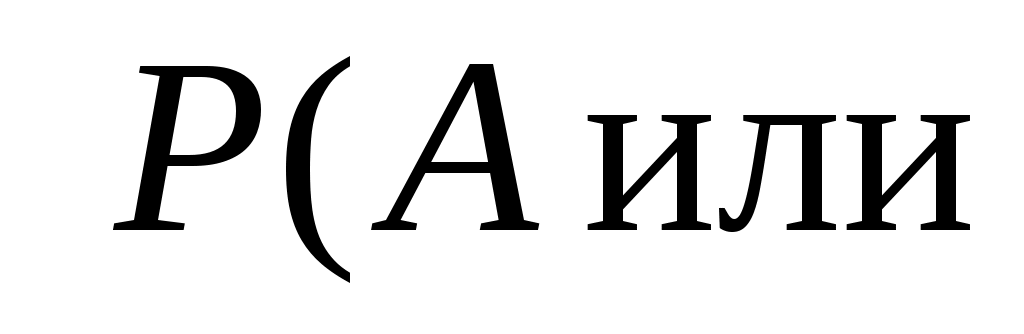 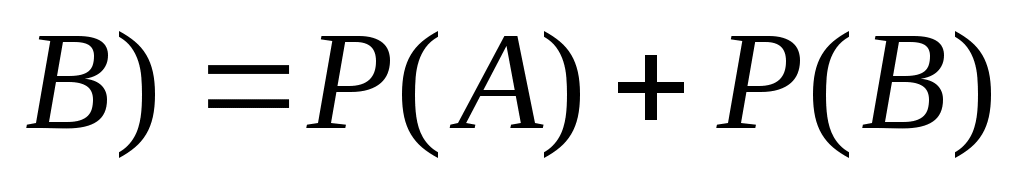
Теорема умножения вероятностей независимых событий:
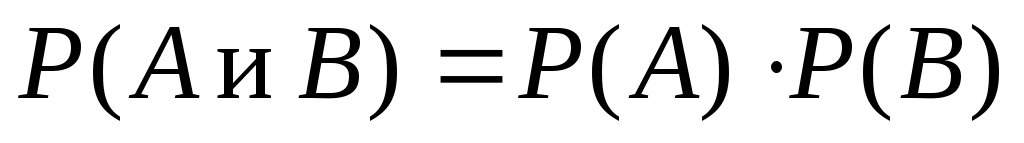
Теорема умножения вероятностей зависимых событий:
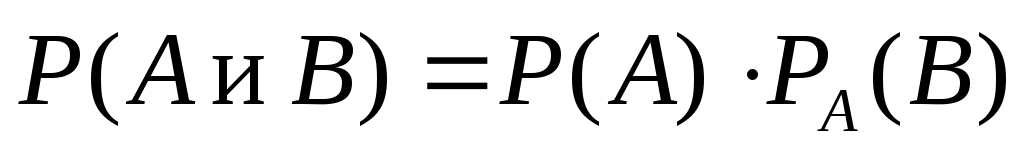
Теорема сложения вероятностей совместных событий:
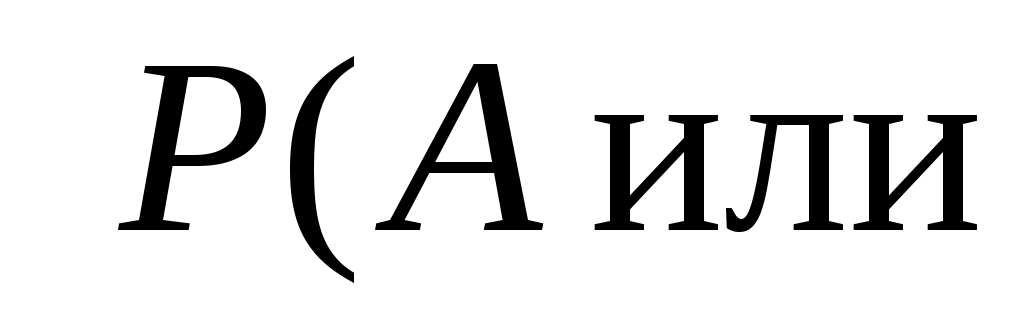 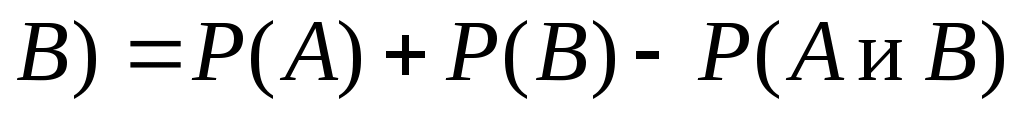
Событие 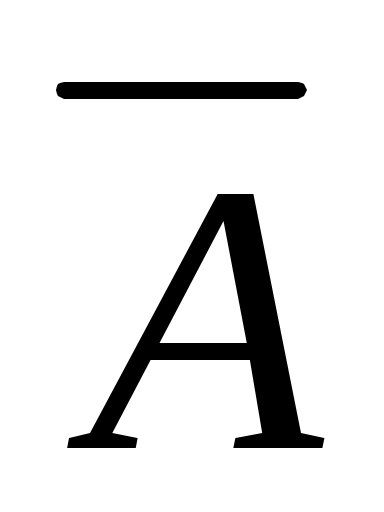 (неA) называется противоположным событию A, если оно наступает тогда и только тогда, когда не наступает событие A. (неA) называется противоположным событию A, если оно наступает тогда и только тогда, когда не наступает событие A.
Пример 4: а) Событие A – изделие бракованное, тогда 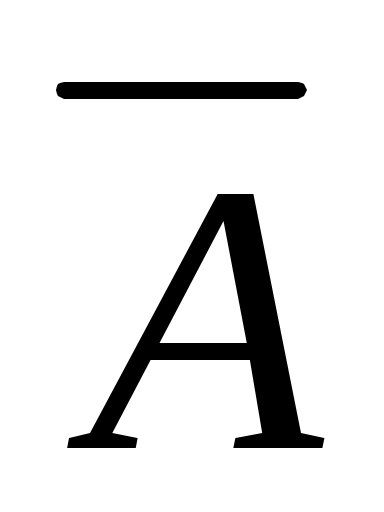 – изделие без брака; б) B – студент сдал экзамен, тогда событие – изделие без брака; б) B – студент сдал экзамен, тогда событие 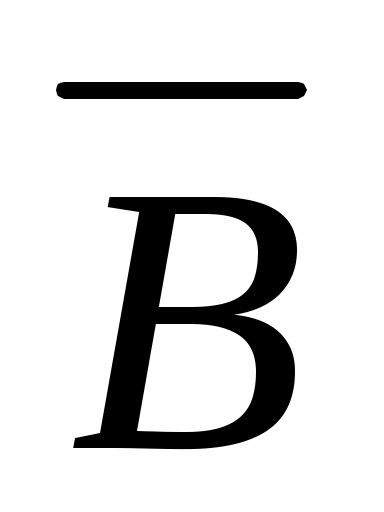 – студент не сдал экзамен; с) С – хотя бы один лотерейный билет выиграл, тогда – студент не сдал экзамен; с) С – хотя бы один лотерейный билет выиграл, тогда 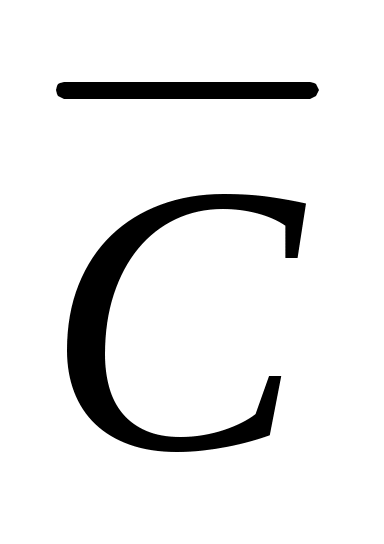 – ни один билет не выиграл. Из приведенных примеров видно, что противоположное событие можно сформулировать путем простого логического отрицания. – ни один билет не выиграл. Из приведенных примеров видно, что противоположное событие можно сформулировать путем простого логического отрицания.
Вероятность противоположного события находится по формуле
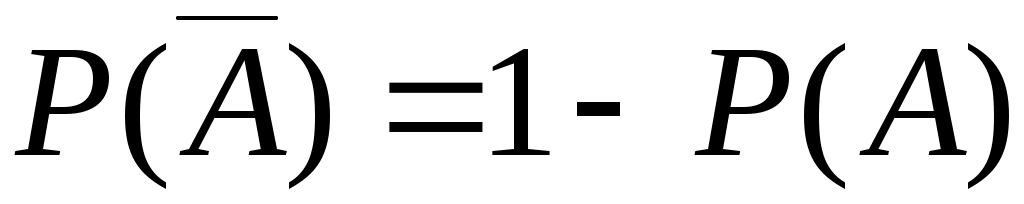
Задача. В партии из 100 одинаковых по внешнему виду изделий смешаны 40 шт. первого сорта и 60 шт. второго сорта. Найти вероятность того, что взятые наугад два изделия окажутся:
а) оба первого сорта;
б) разных сортов;
в) хотя бы одно из них первого сорта.
Найти указанные вероятности, если изделия выбираются по схеме выборки 1) с возвращением; 2) без возвращения.
Решение. 1). Рассмотрим вначале случай, когда изделия выбирают по схеме выборки с возвращением. В этом случае первое изделие из партии выбирается случайным образом, определяется его сортность, затем оно возвращается в партию и может быть выбрано повторно. Второе изделие выбирается из той же партии, состоящей из ста изделий. Обозначим:
событие  – первое взятое изделие I сорта, – первое взятое изделие I сорта,
событие 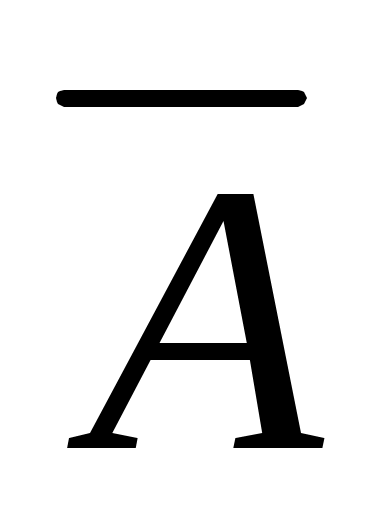 – первое взятое изделие II сорта (не I сорта), – первое взятое изделие II сорта (не I сорта),
событие 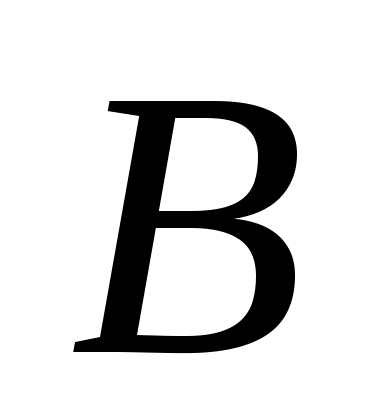 - второе взятое изделие I сорта , - второе взятое изделие I сорта ,
событие 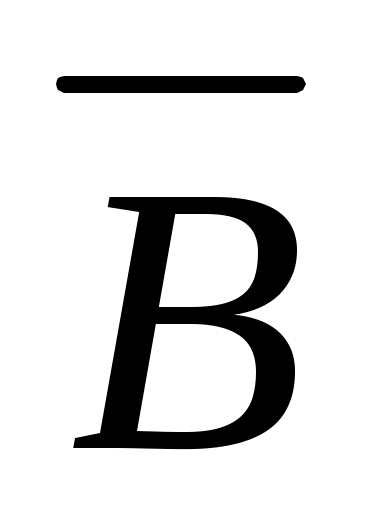 – второе взятое изделие II сорта (не I сорта). – второе взятое изделие II сорта (не I сорта).
Заметим, что в рассматриваемом случае события А и В независимые, так как вероятность события В не зависит от того, какого сорта было выбрано первое изделие.
а) Р(оба изделия I сорта) = Р(Aи B) = Р (A) Р(B) = 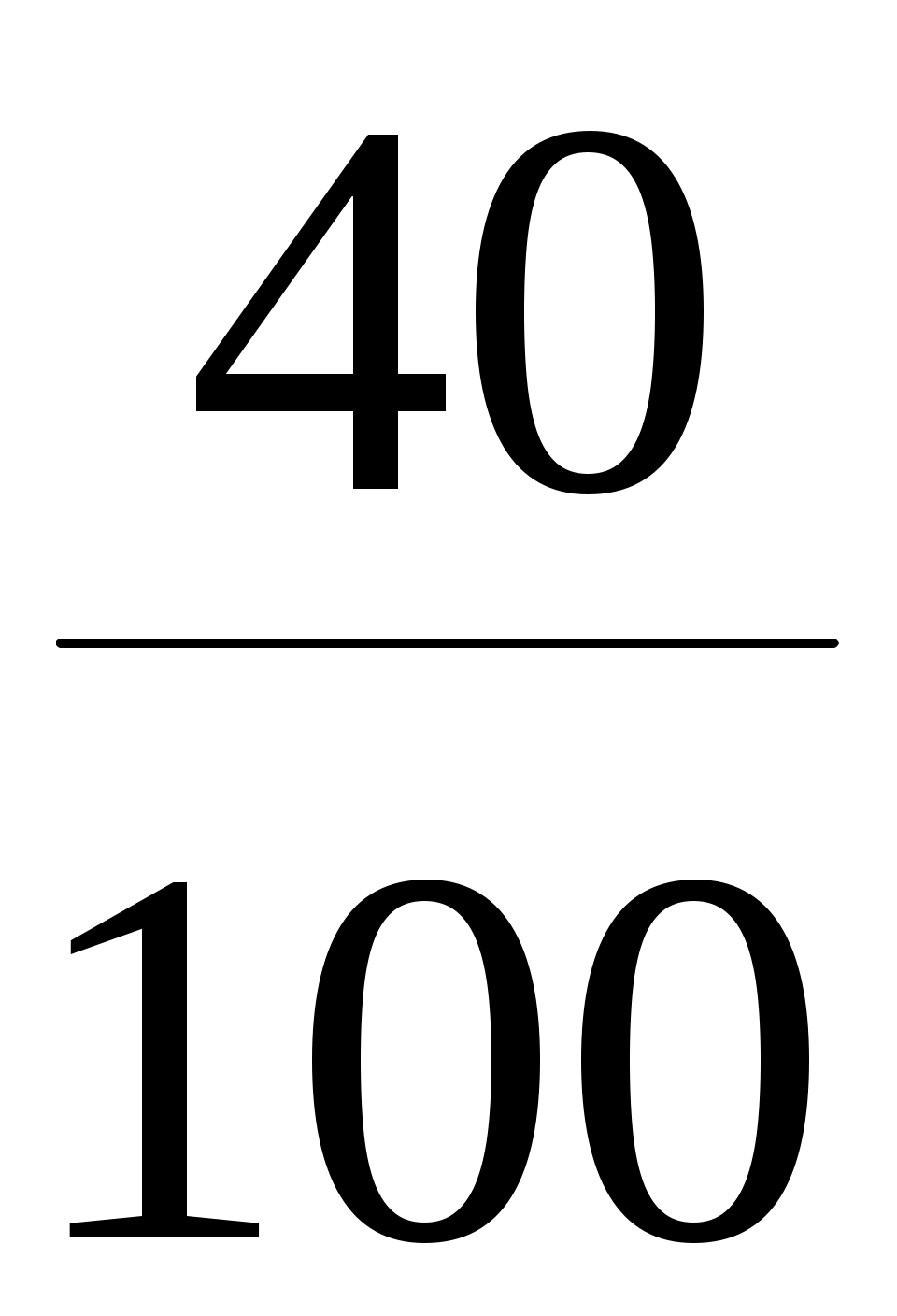 . . 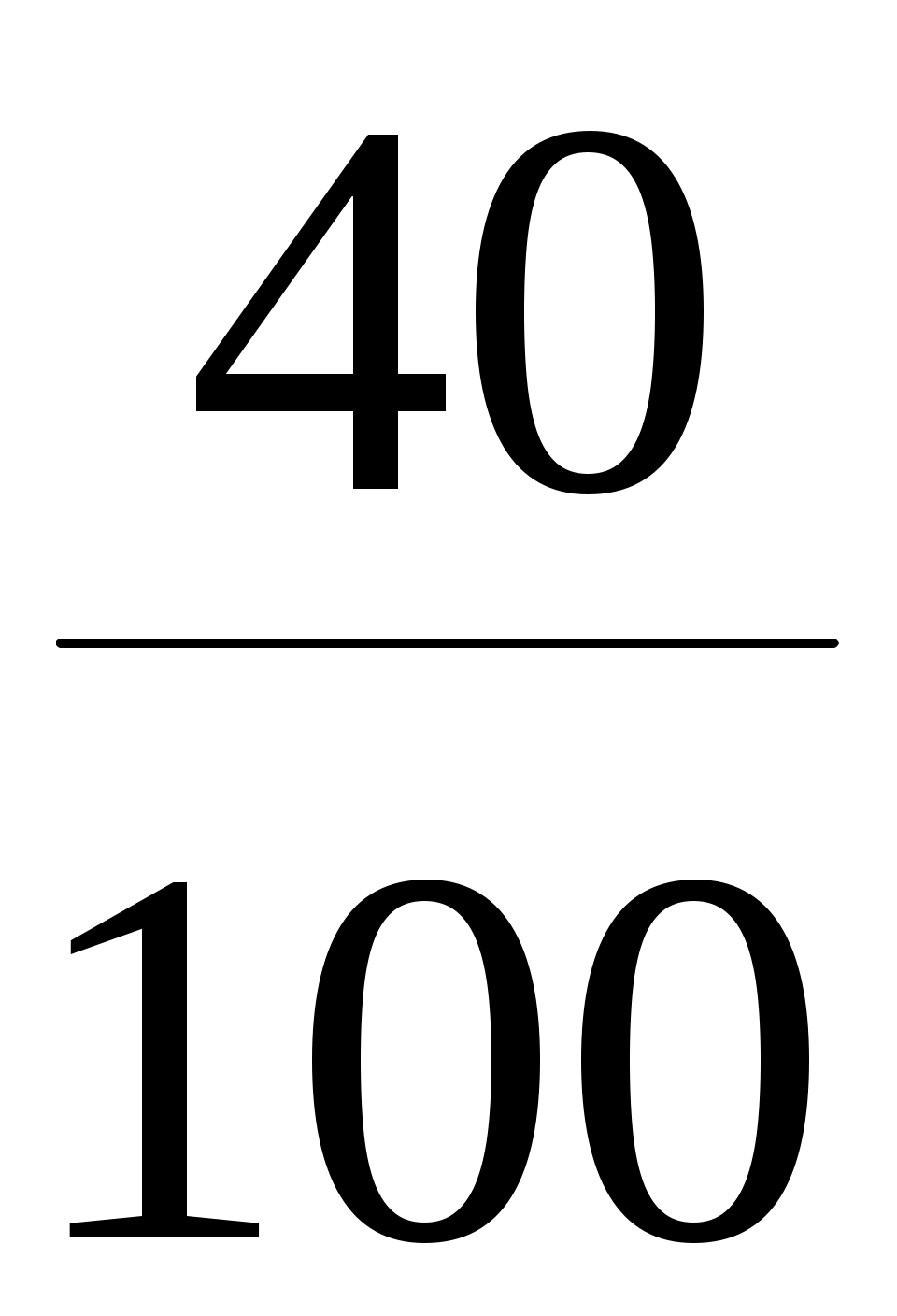 = 0,16. = 0,16.
Здесь мы воспользовались теоремой умножения вероятностей независимых событий.
б) Р (изделия разных сортов) = Р(Aи 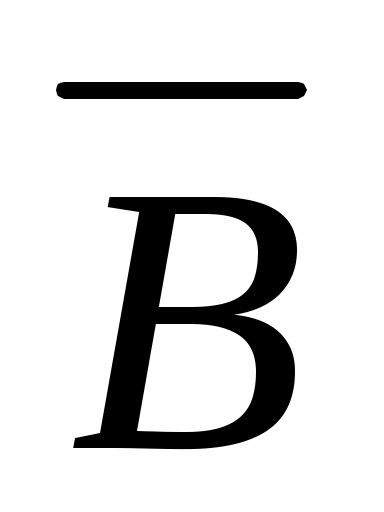 или или 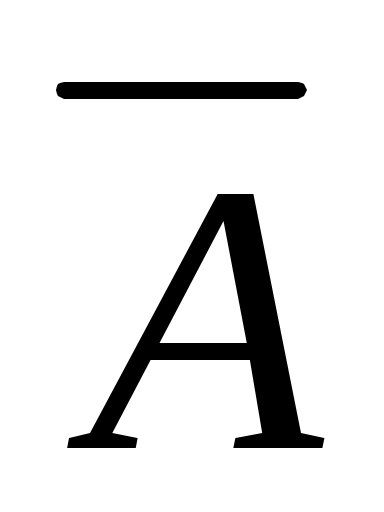 и B) = и B) =
= Р(A) Р(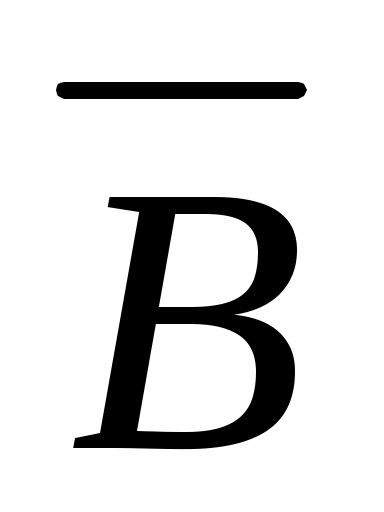 ) + Р( ) + Р(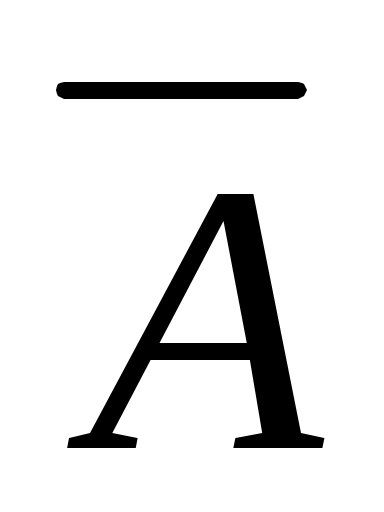 ) Р(B) = ) Р(B) = 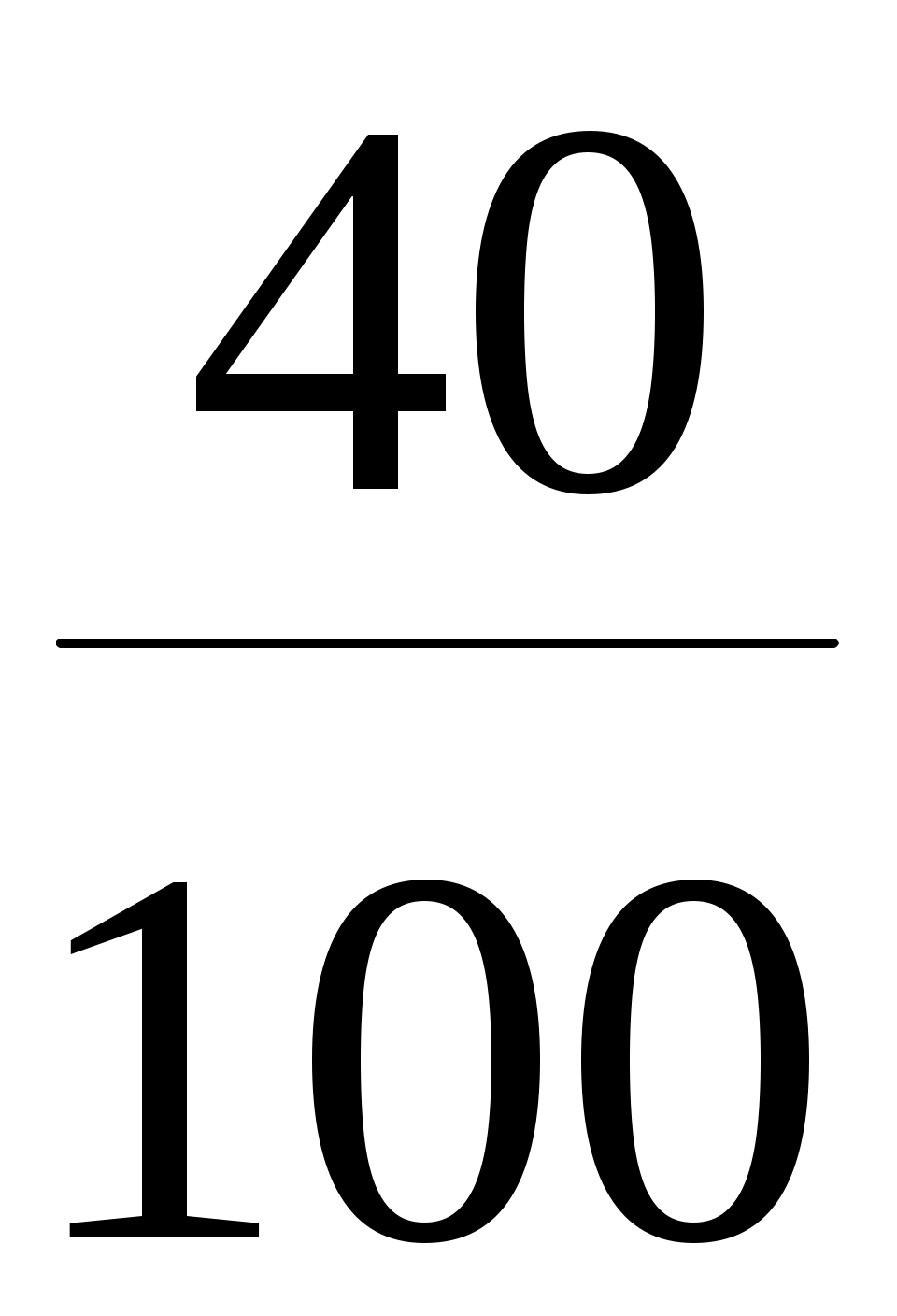 . . 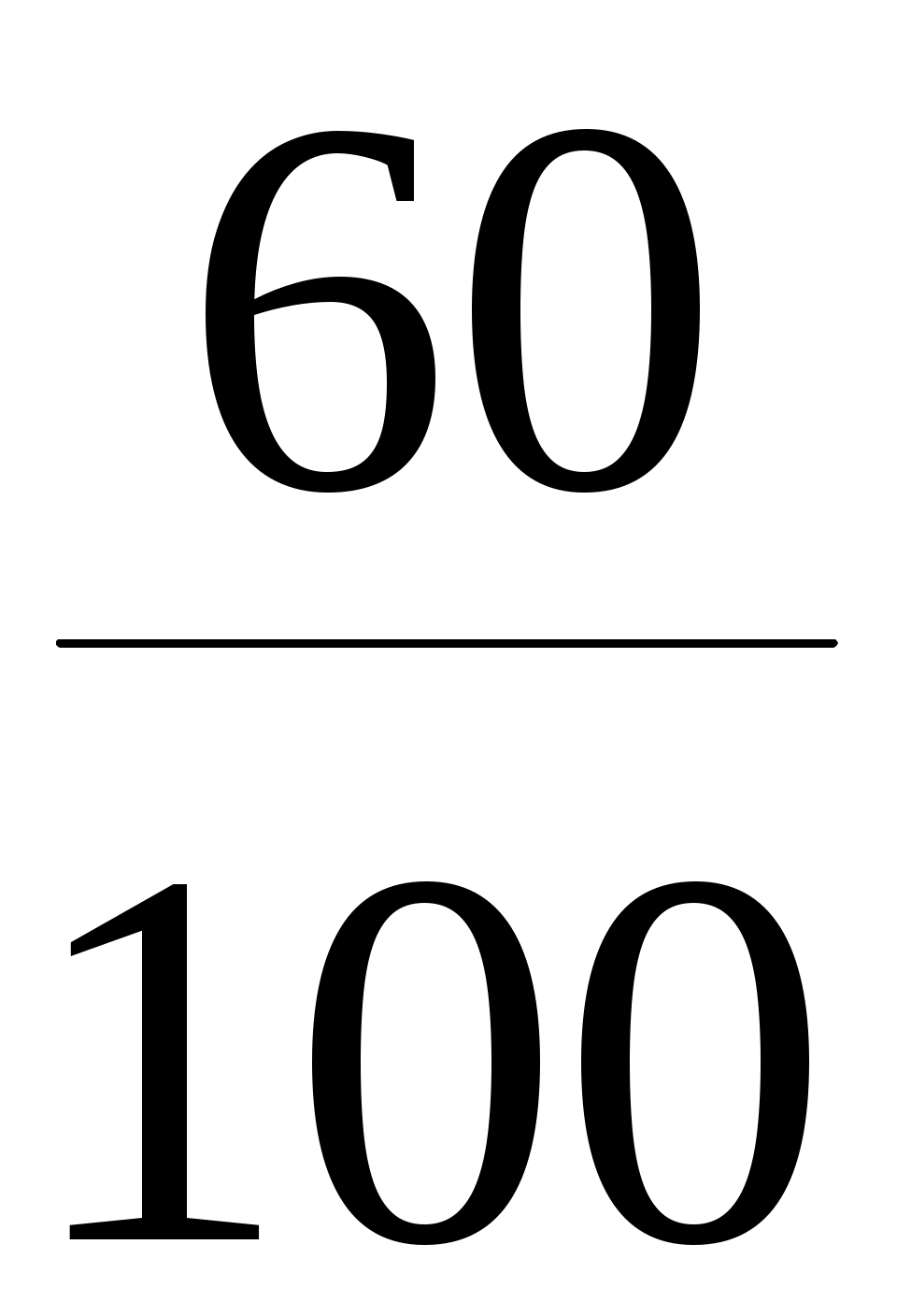 + +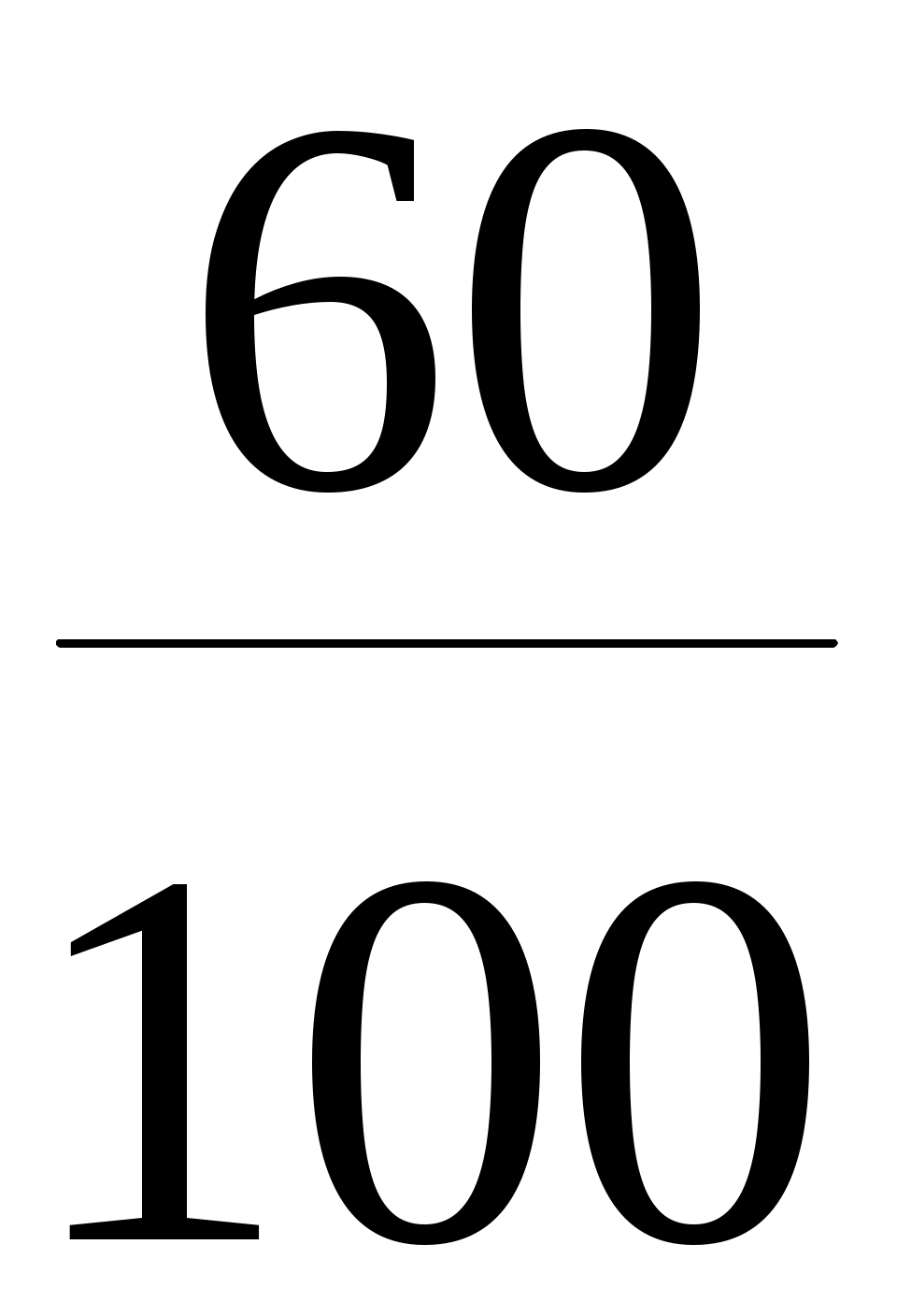 . .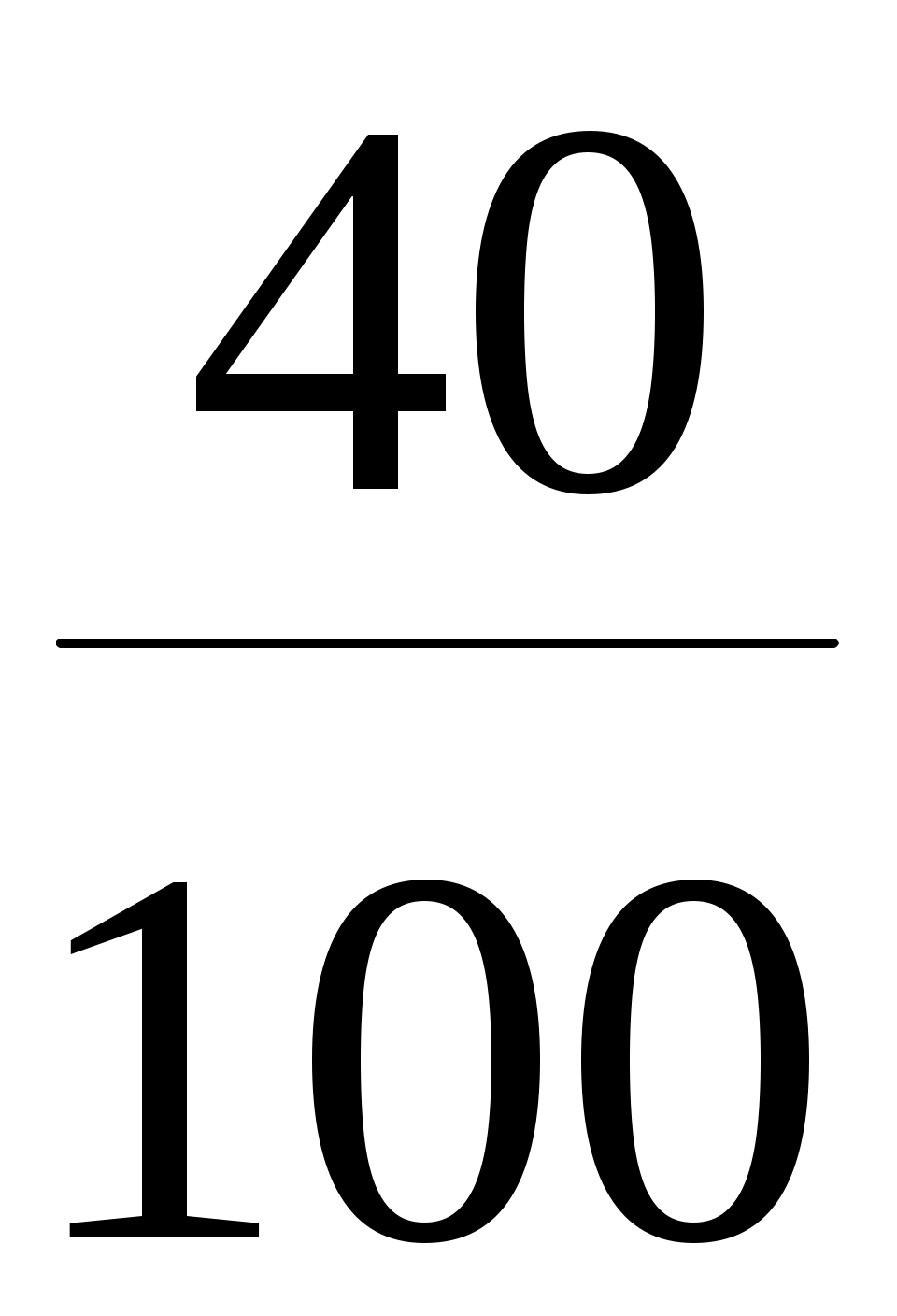 = 0,4 0,6 + = 0,4 0,6 +
+ 0,6 0,4 = 0,48.
Здесь мы воспользовались теоремой сложения несовместных событий и теоремой умножения для независимых событий.
в) Р (хотя бы одно изделие I сорта) = 1 – Р (нет ни одного
изделия I сорта) = 1 – Р (оба изделия II сорта) = 1 – Р( и и 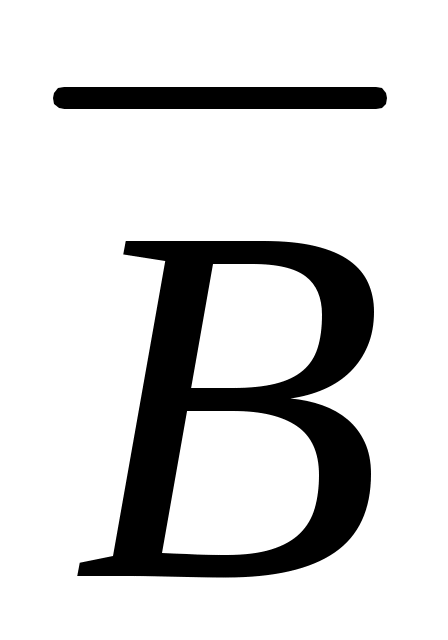 ) = 1 – Р ( ) = 1 – Р ( ) × Р ( ) × Р (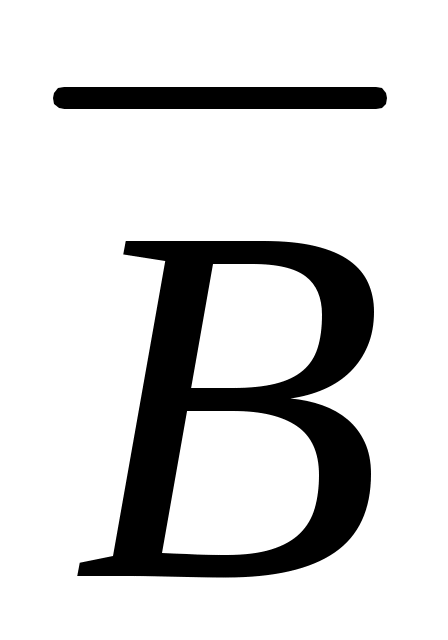 ) = 1 – ) = 1 – 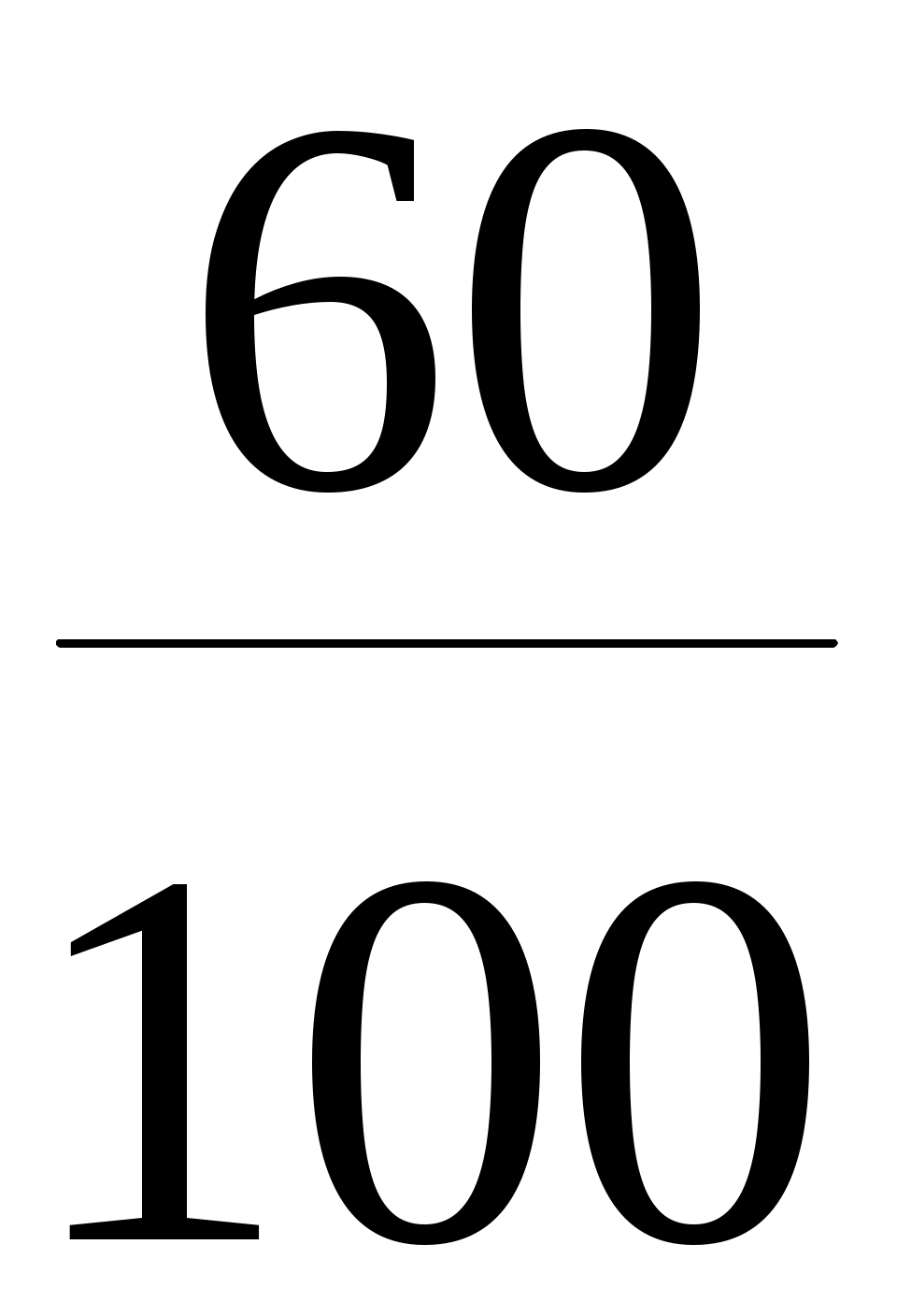 . .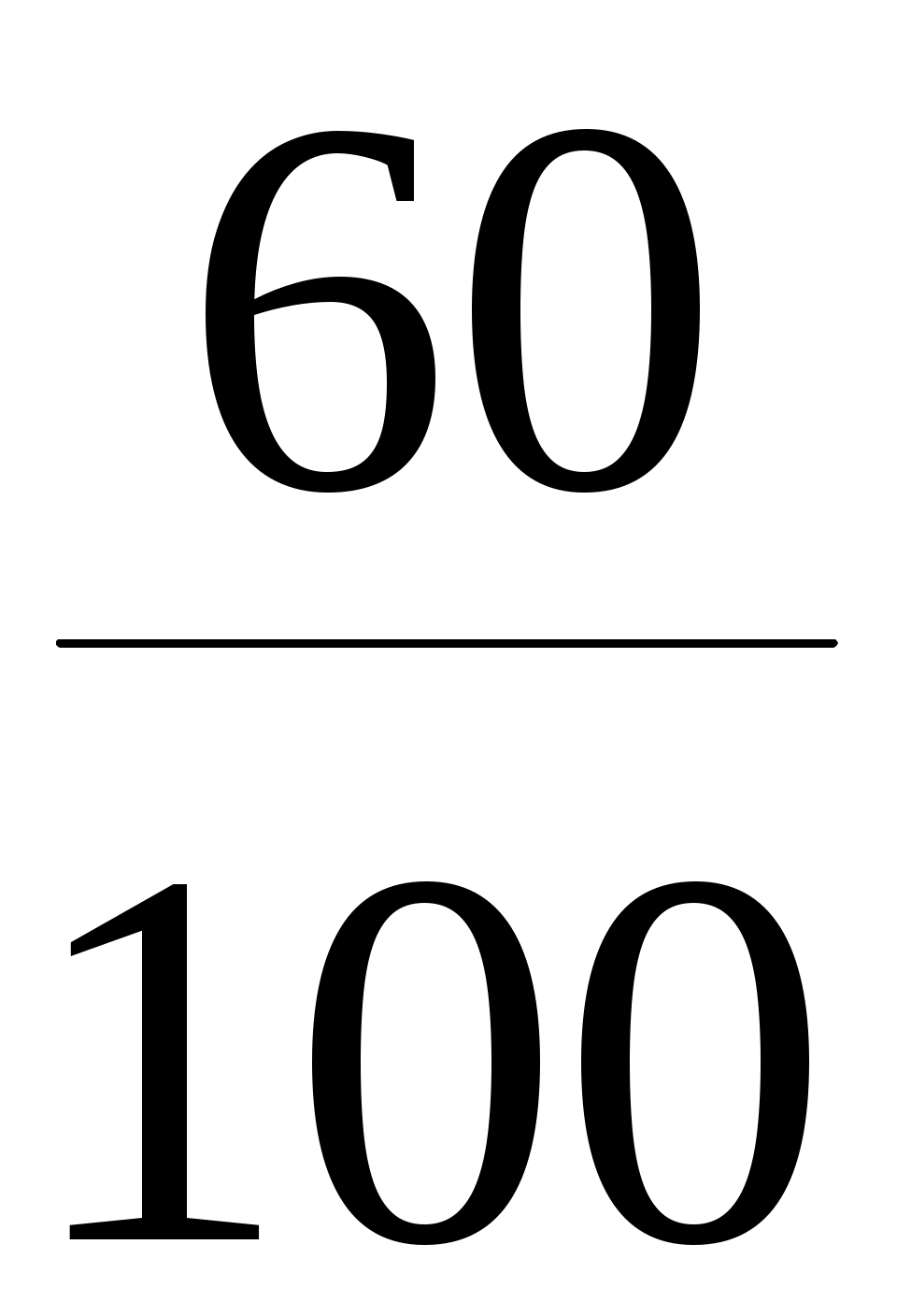 = 0,64. = 0,64.
Здесь мы воспользовались формулой для нахождения вероятности противоположного события.
2). Далее, рассмотрим случай, когда изделия выбирают по схеме выборки без возвращения. В этом случае первое изделие из партии выбирается случайным образом, определяется его сортность, но в партию оно не возвращается. Второе изделие выбирается из оставшихся изделий. Подчеркнем, что в этом случае события А и В являются зависимыми. Найдем вероятности событий.
а) Р(оба изделия I сорта) = Р(Aи B) = Р(А) ∙ РА (В) = 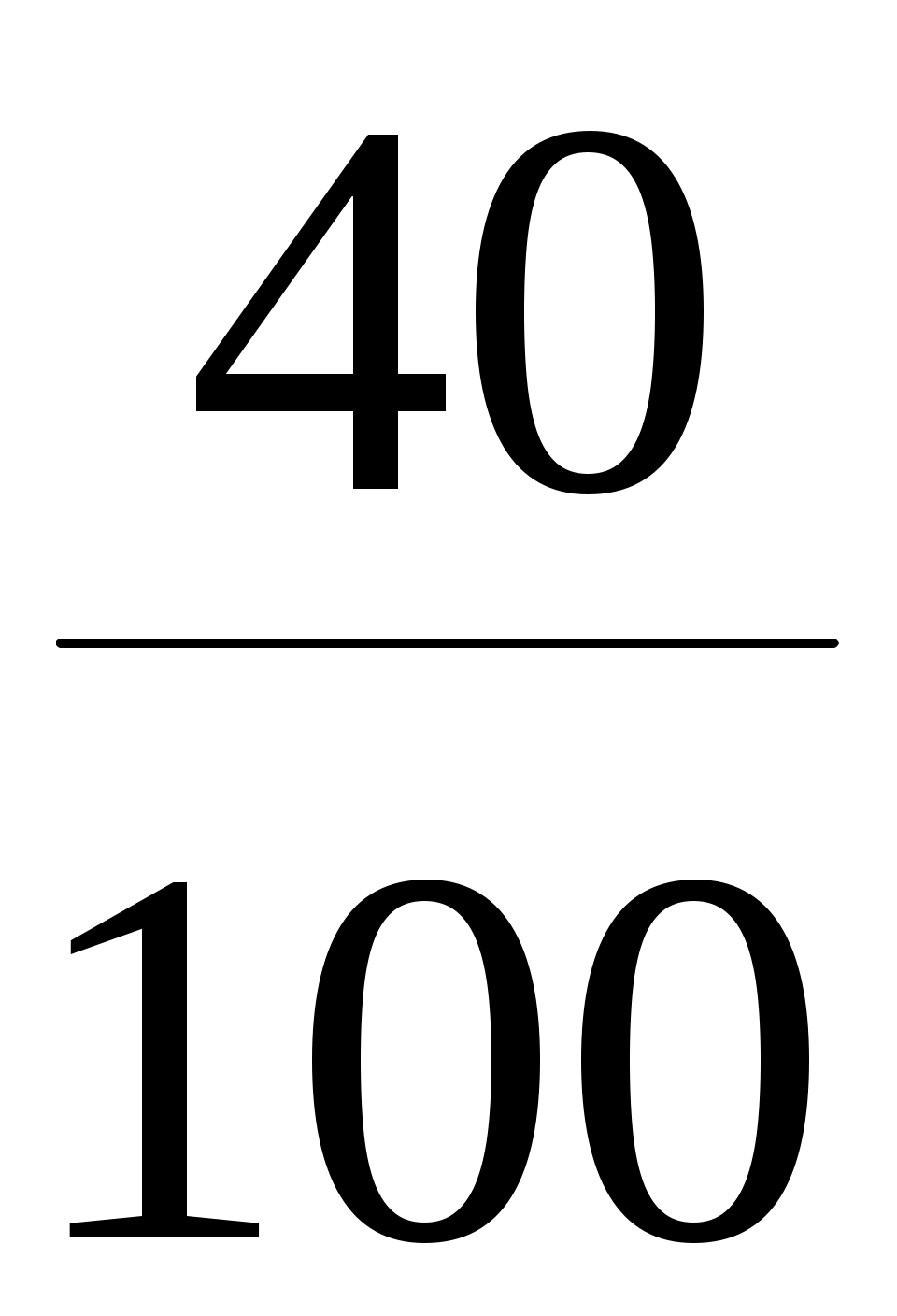 . . 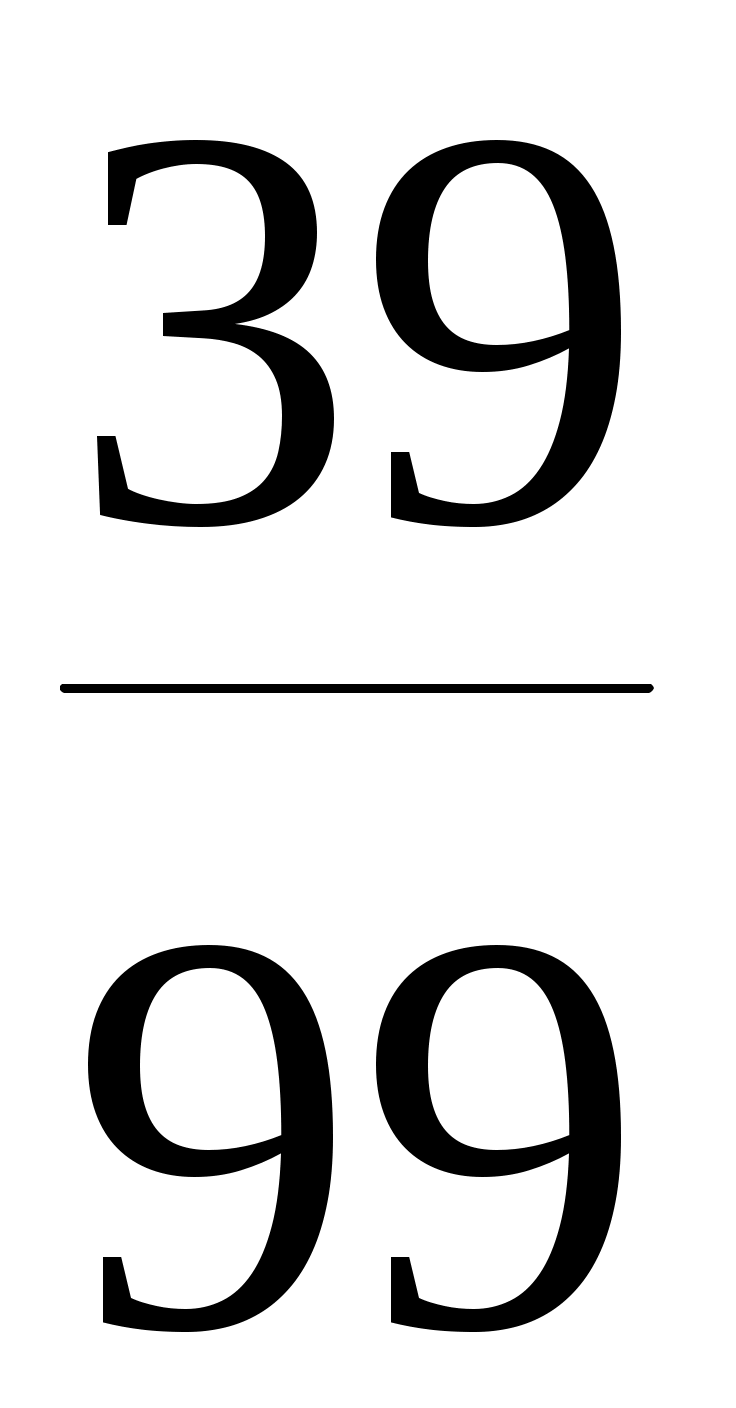 = =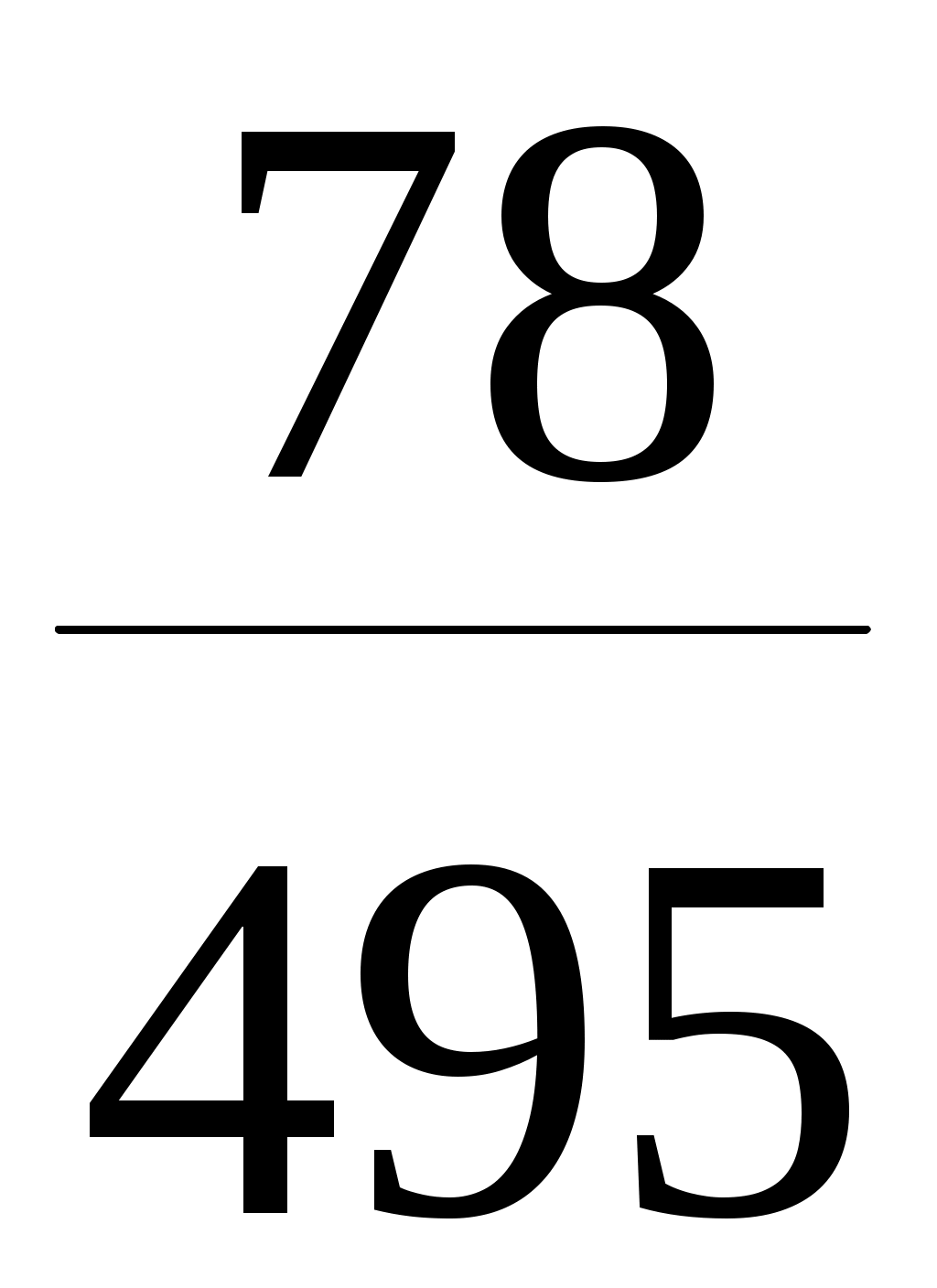 . .
Здесь мы воспользовались теоремой умножения вероятностей для зависимых событий. Поясним более подробно, как были найдены вероятности Р(А) и РА (В). При выборе первого изделия общее число исходов равно 100 (по числу изделий) и все они равновозможны. Благоприятствующих из них событию А – 40 (по числу изделий I сорта). По классическому определению вероятности Р(А) = m / n = 40 /100. Найдем условную вероятность РА (В), то есть вероятность выбрать второе изделие I сорта при условии, что первое выбранное изделие было также I сорта. Посмотрим, как изменился состав партии после того, как выбрали первое изделие: изделий в партии осталось 100 – 1 = 99 (первое забрали), среди них изделий первого сорта осталось 40 – 1 = 39 (выбранное первое изделие было I сорта ). Далее, выбираем второе изделие: общее число исходов этого испытания 99 (по числу оставшихся изделий). Благоприятствующих из них событию В – 39 (по числу оставшихся изделий I сорта). По классическому определению вероятности
РА(В) = m / n = 39 /99.
б) Р (изделия разных сортов) = Р(Aи 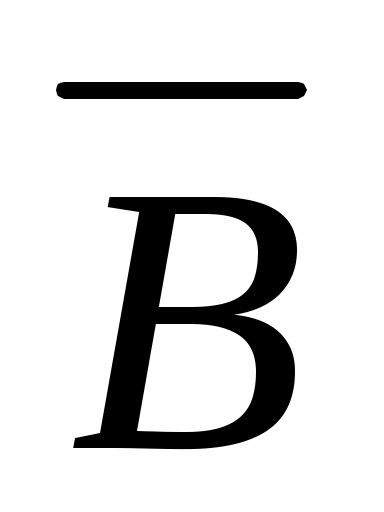 или или 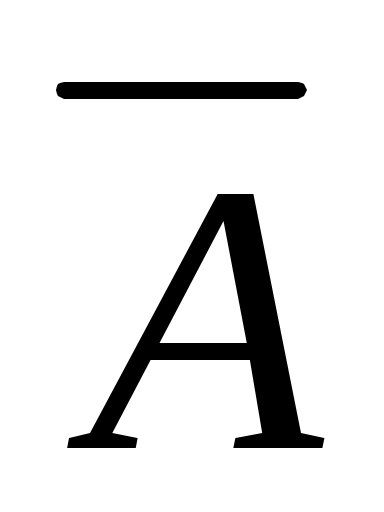 и B) = и B) =
= Р(A) РА(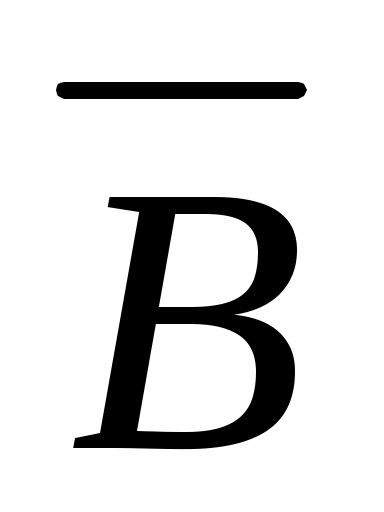 ) + Р( ) + Р(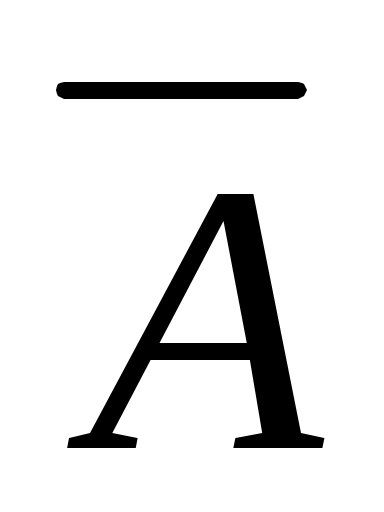 ) Р ) Р  (B) = (B) = 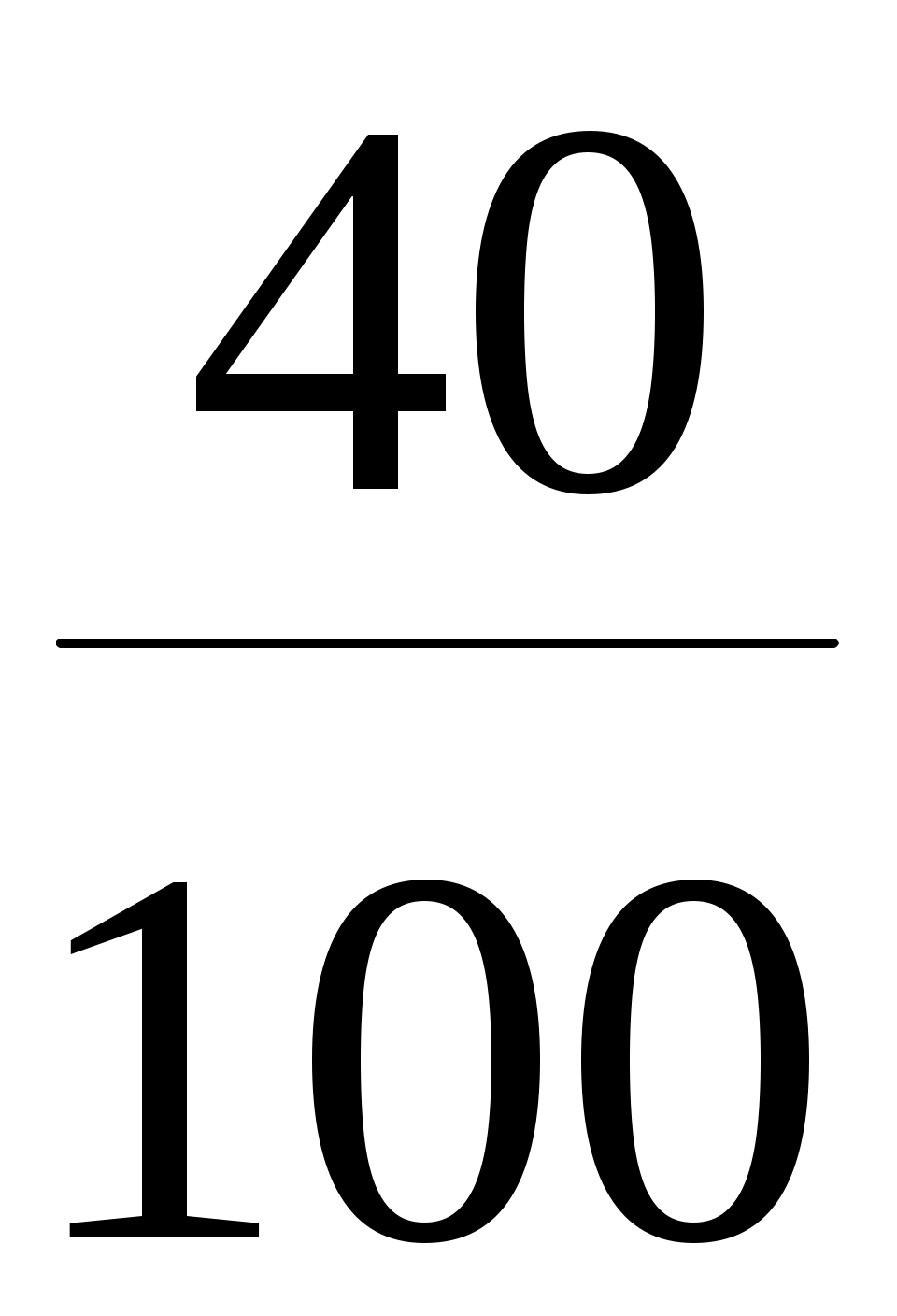 . . 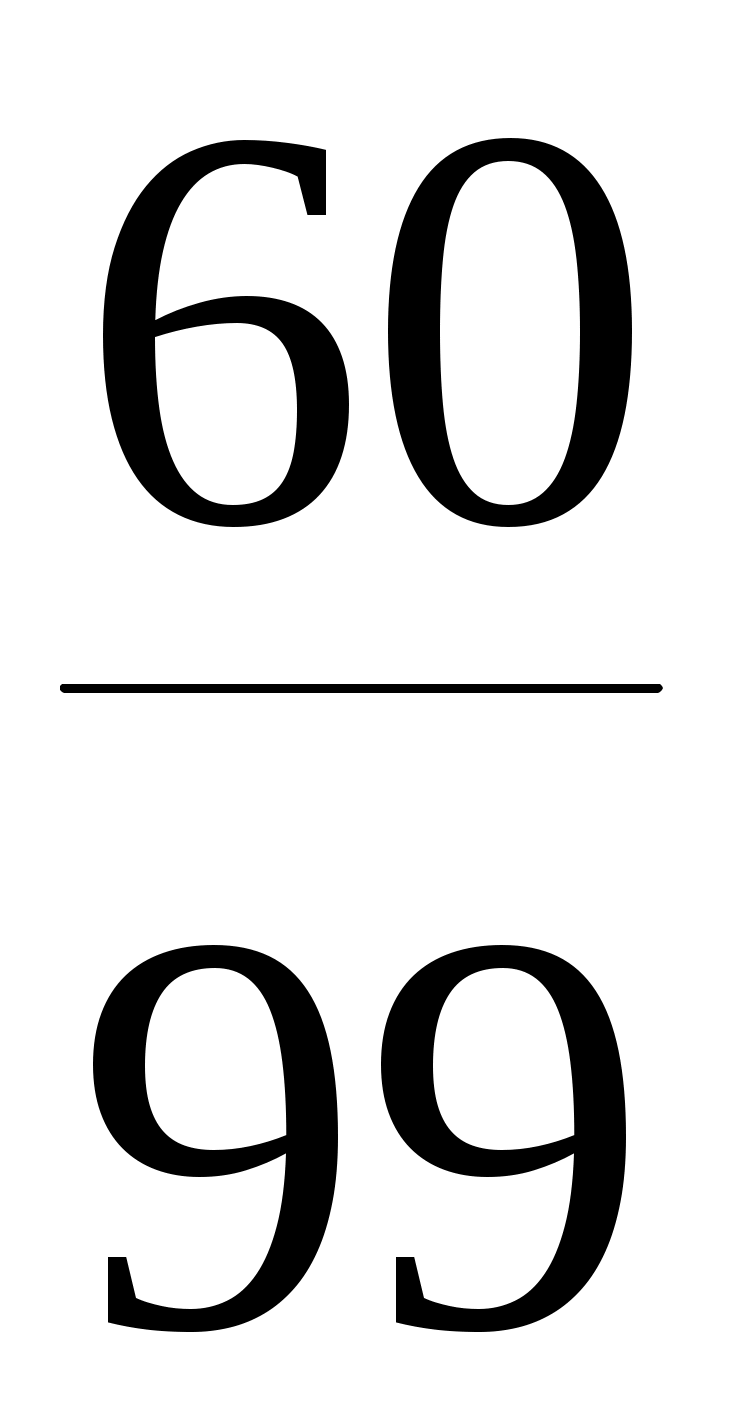 + +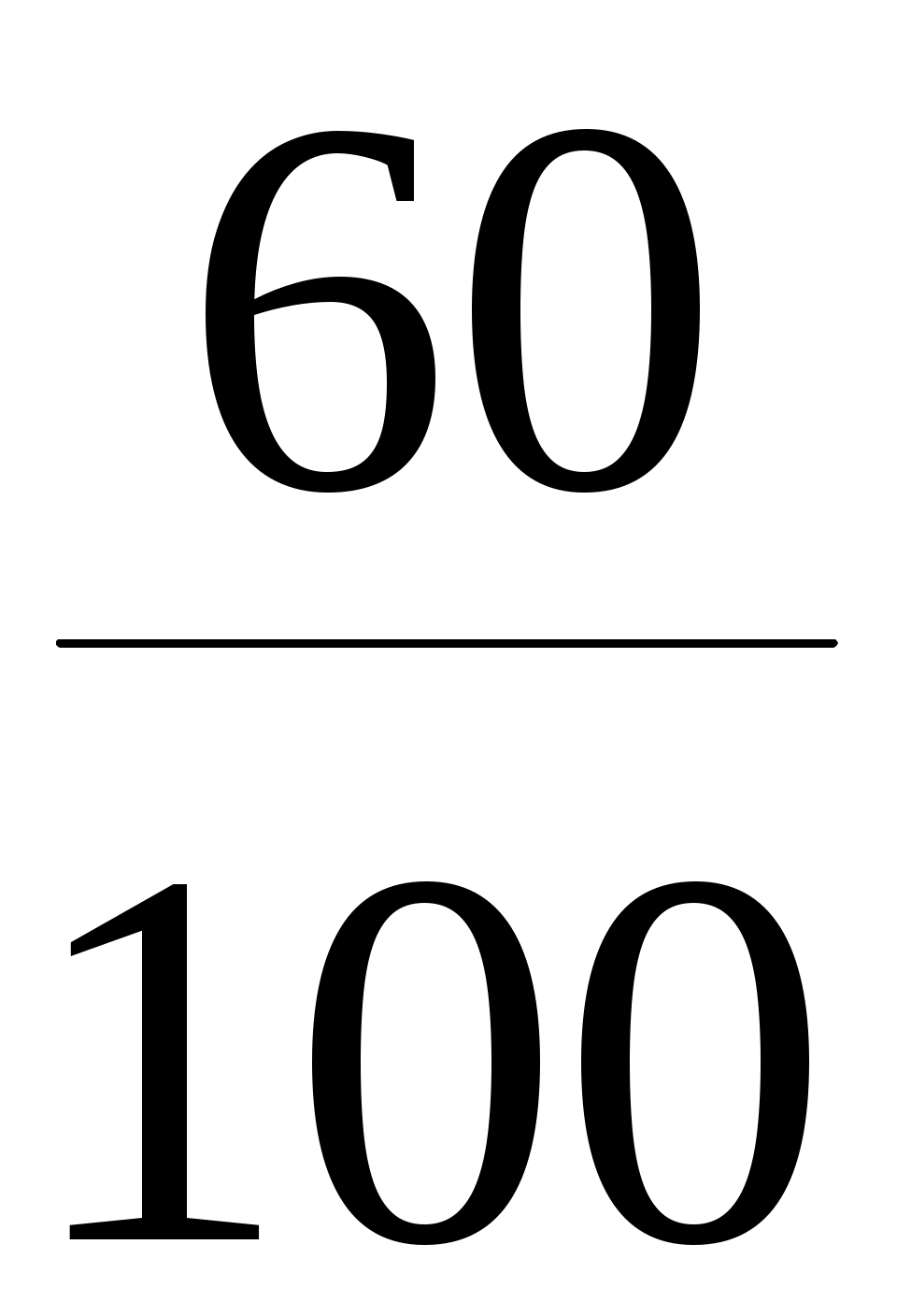 . .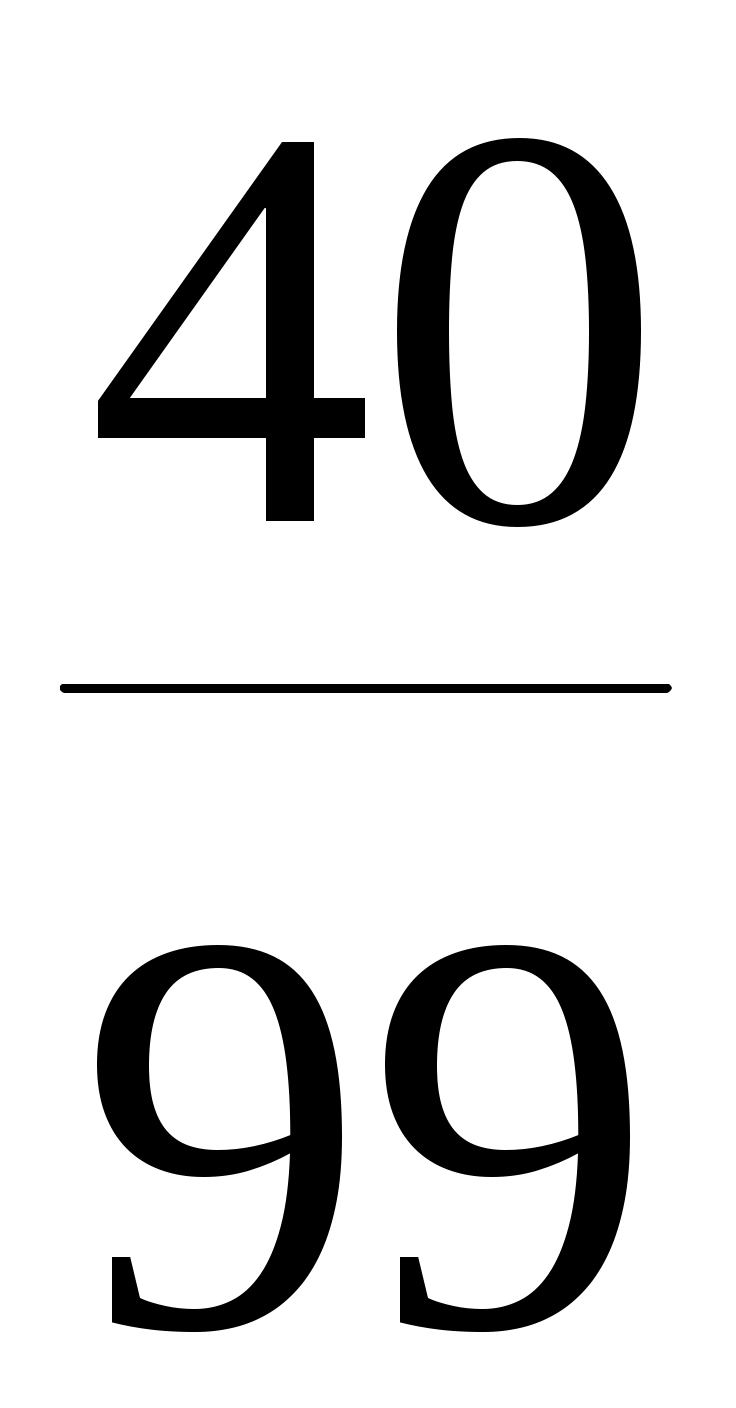 = = 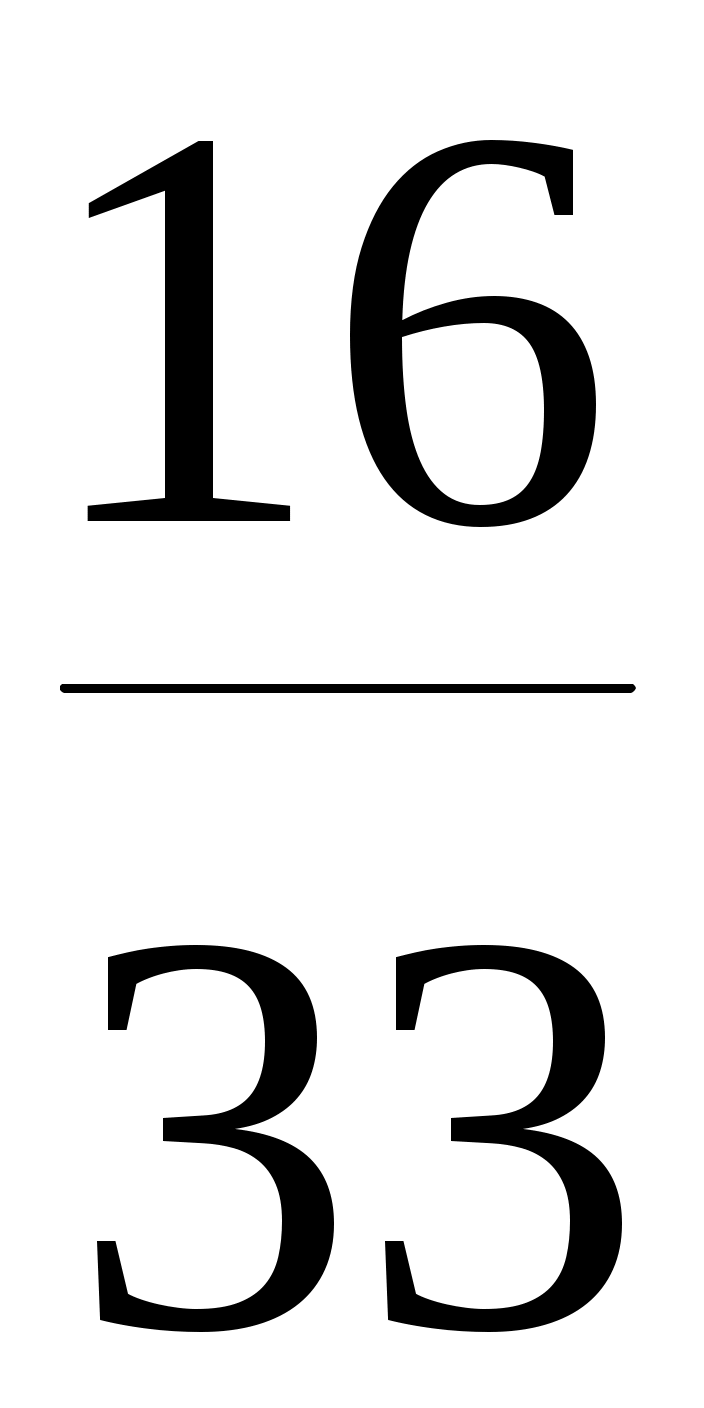 . .
Здесь мы воспользовались теоремой сложения вероятностей несовместных событий и теоремой умножения вероятностей зависимых событий.
в) Р (хотя бы одно изделие I сорта) = 1 – Р (ни одного нет
изделия I сорта) = 1 – Р (оба изделия II сорта) = 1 – Р( и и 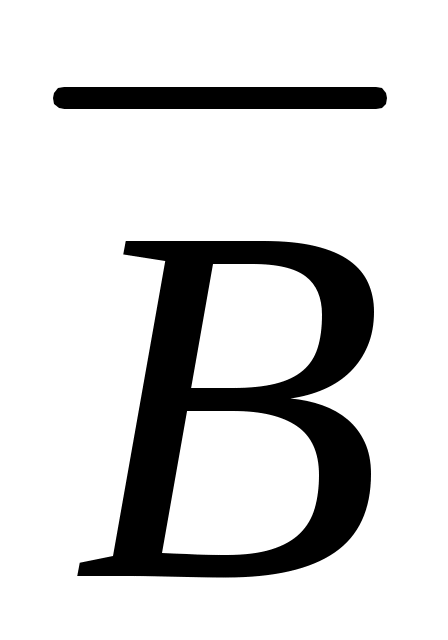 ) = ) =
1 – Р ( ) × Р ) × Р  ( (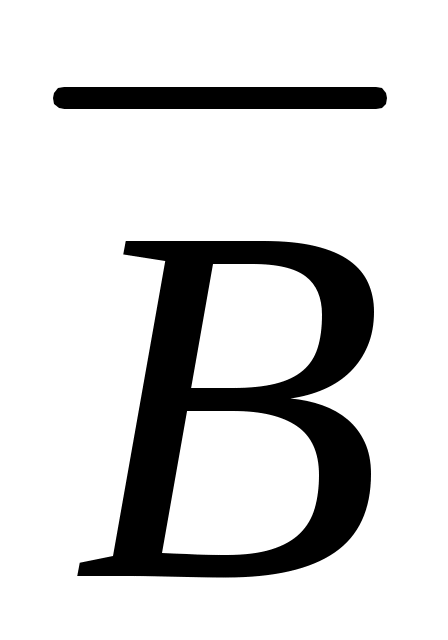 ) = 1 – ) = 1 – 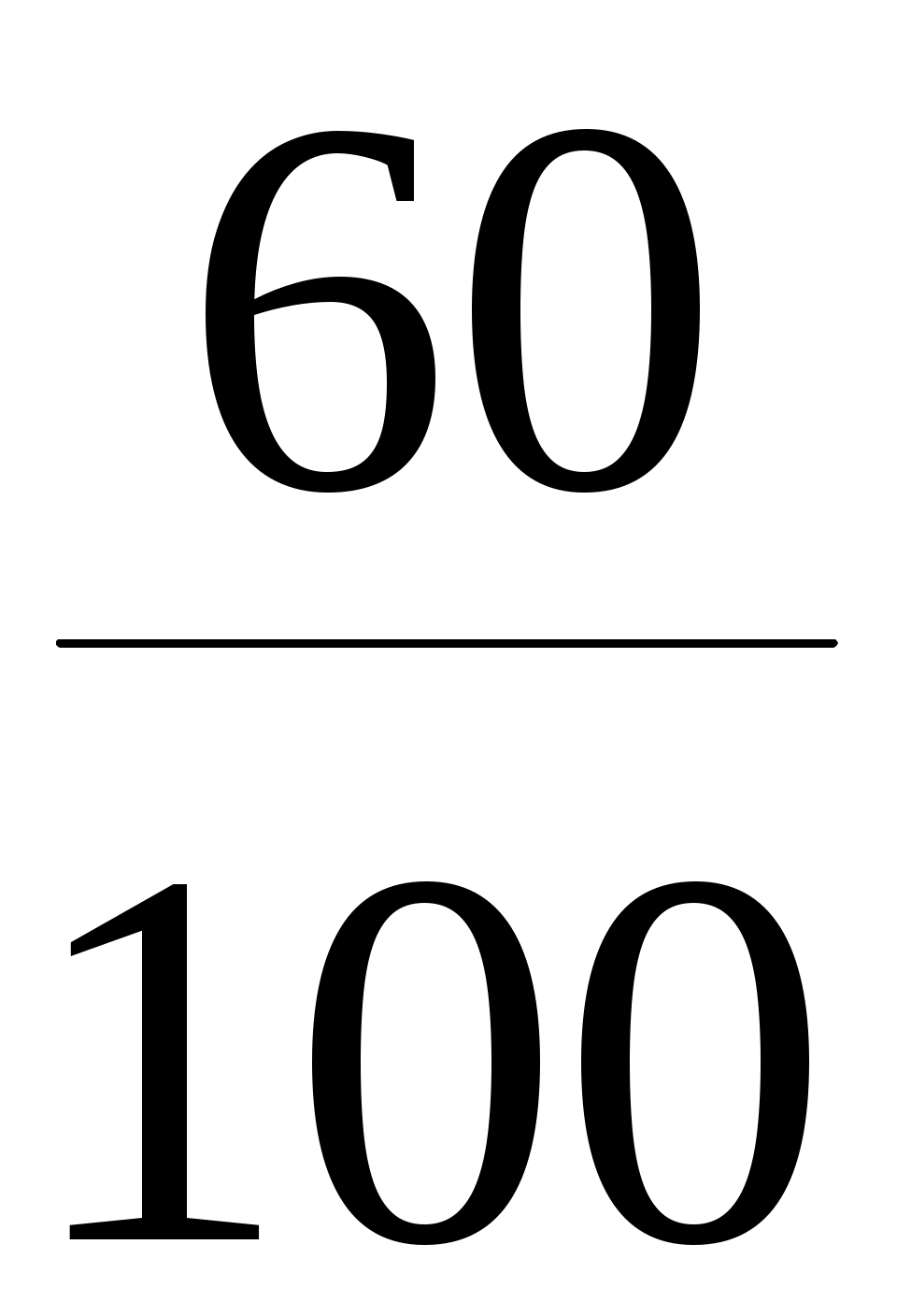 . .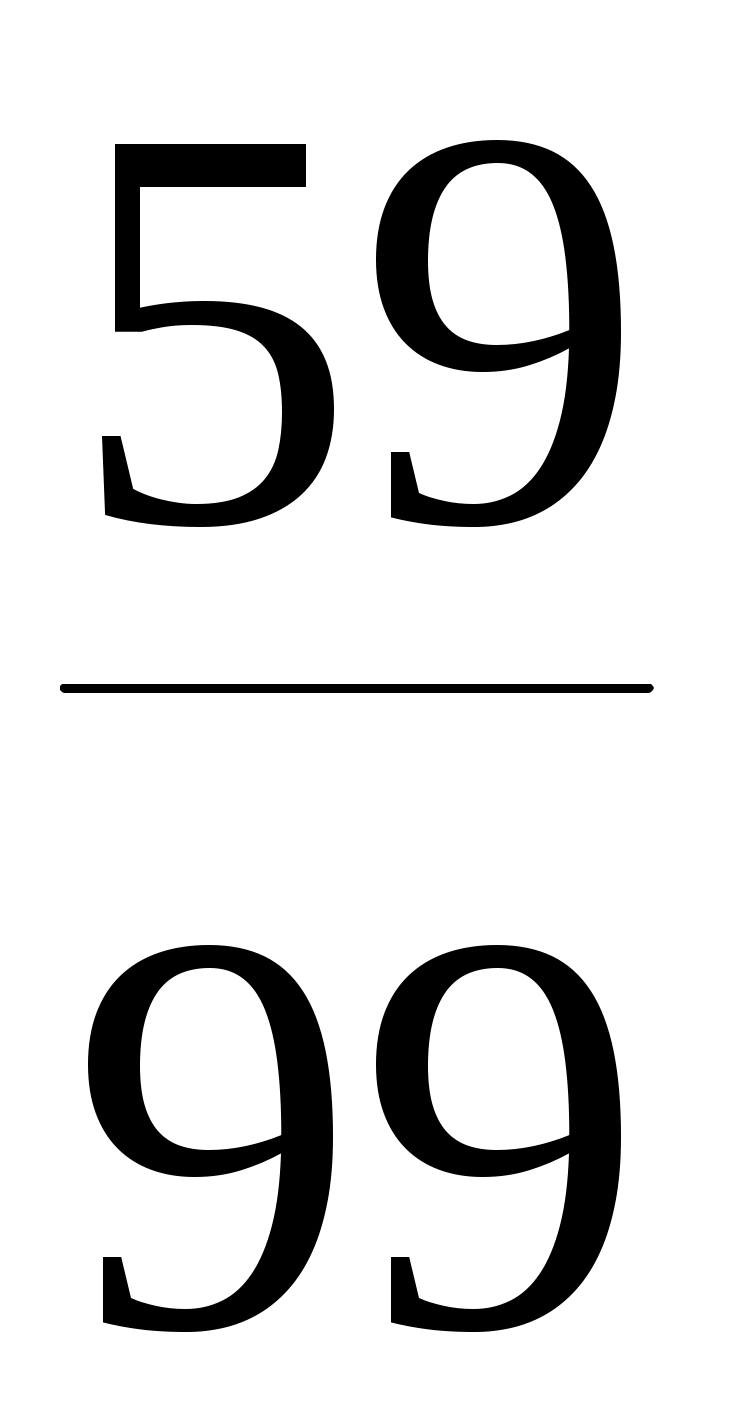 = = 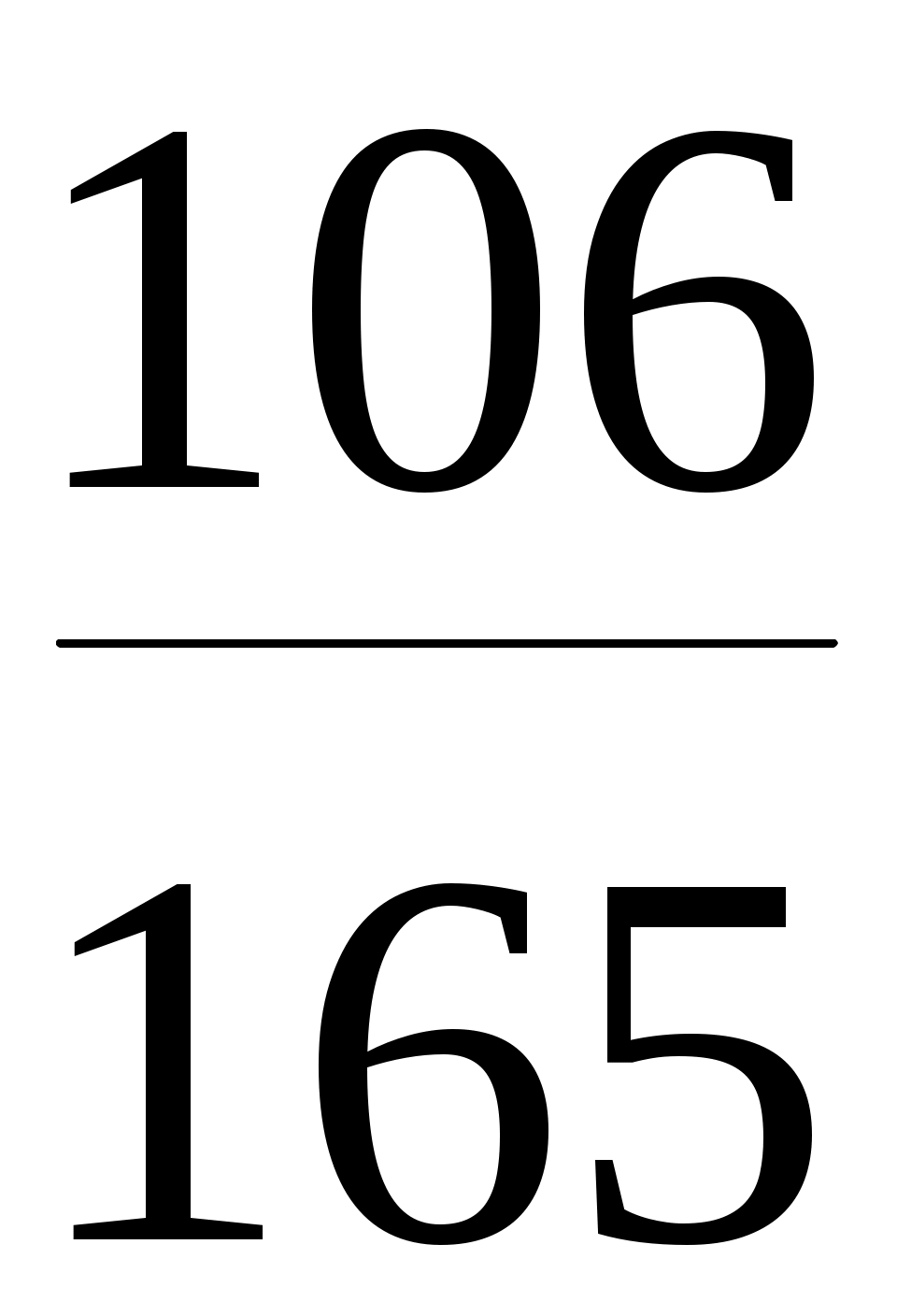 . .
Задачи 71 -80
71. Вероятность того, что новый товар будет пользоваться спросом на рынке, если конкурент не выпустит в продажу аналогичный продукт, равна 0,75 , а при наличии конкурирующего товара равна 0,35. Вероятность выпуска конкурентом товара равна 0,45. Найти вероятность того, что товар будет пользоваться спросом.
72. Курс доллара повышается в течение квартала с вероятностью 0,9 и понижается с вероятностью 0,1. При повышении курса доллара фирма рассчитывает получить прибыль с вероятностью 0,85; при понижении – с вероятностью 0,5. Найти вероятность того, что фирма получит прибыль.
73. На строительство объекта поступают железобетонные плиты от четырех цементных заводов в количестве 50, 10, 40 и 30 штук соответственно. Каждый из заводов допускает при изготовлении плит брак (несоответствие ГОСТ), составляющий соответственно 1%, 5%, 2% и 3%. Какова вероятность того, что наугад взятая плита будет удовлетворять требованиям ГОСТ?
74. В цехе трудятся 3 мастера и 6 их учеников. Мастер допускает брак при изготовлении изделия с вероятностью 0,05; а ученик – с вероятностью 0,15. Какова вероятность, что взятое наугад изделие будет бракованным?
75. В данный район изделия поставляются двумя фирмами. Среди продукции первой фирмы стандартные изделия составляют 90%, у второй фирмы этот показатель 85%. Какова вероятность, что взятое наугад изделие оказалось стандартным, если вероятность того, что оно поставлено первой фирмой, равна 0,4?
76. В магазине имеются два телевизора с импортными и девять с отечественными трубками. Вероятность выхода из строя в течение гарантийного срока телевизора с импортной трубкой равна 0,005; с отечественной трубкой равна 0,01. Найти вероятность того, что купленный в магазине телевизор выдержит гарантийный срок.
77. В двух ящиках находятся радиолампы. В первом ящике 3% ламп - бракованные, во втором ящике бракованные лампы составляют 5%. Из наудачу выбранного ящика выбирается одна лампа. Найти вероятность того, что она будет без брака.
78. Страховая компания разделяет застрахованных клиентов по классам риска: I класс – малый риск, II класс – средний риск, III класс – большой риск. Среди этих клиентов 50 % - первого класса риска, 30% - второго и 20% - третьего. Вероятность необходимости выплачивать страховое вознаграждение для первого класса риска равна 0,01, второго 0,03, третьего 0,08. Какова вероятность того, что застрахованный получит денежное вознаграждение за период страхования?
79. Вся продукция цеха проверяется двумя контролерами, причем первый контролер проверяет 55% изделий, а второй – остальные. Вероятность того, что первый контролер пропустит нестандартное изделие, равна 0,01, а для второго контролера эта вероятность 0,02. Какова вероятность, что взятое наугад изделие, маркированное как стандартное, оказалось нестандартным?
80. Вероятность изготовления изделия с браком на данном предприятии равна 0,04. Перед выпуском изделие подвергается упрощенной проверке, которая в случае бездефектного изделия пропускает его с вероятностью 0,92, а в случае изделия с дефектом – с вероятностью 0,03. Определить, какая часть изготовленных изделий выходит с предприятия.
Методические указания к решению задач 71 – 80
Формула полной вероятности
События H1 , H2 , …, Hn образуют полную группу, если они попарно несовместны и в результате испытания одно из них обязательно произойдет.
Для таких событий справедливо равенство:
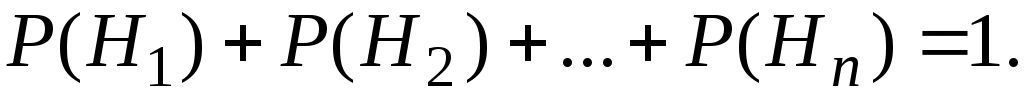
Противоположные событияA и  всегда образуют полную группу, поэтому всегда образуют полную группу, поэтому
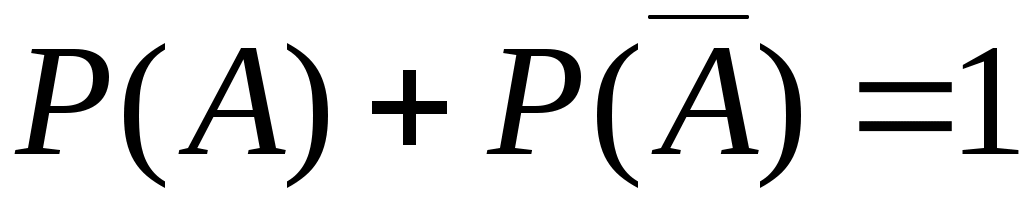 или или 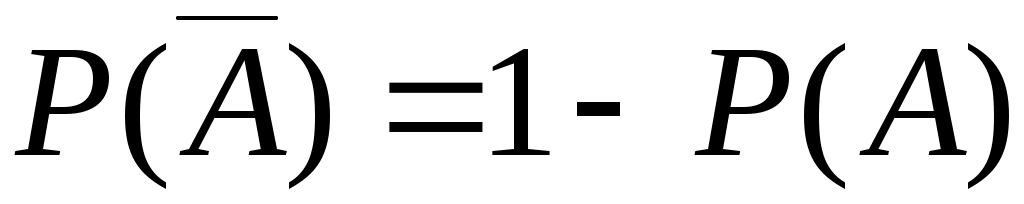 . .
Пусть событие A наступает с одним из событий (гипотез) Hi , тогда вероятность этого события находится по формуле, называемой формулой полной вероятности
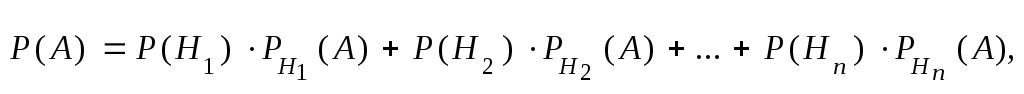
где события H1 , H2 , …, Hn образуют полную группу.
Задача. Два консервных завода поставляют в магазин мясные и овощные консервы, причем первый завод поставляет 75% всей продукции. Доля овощных консервов в продукции первого завода составляет 60%, а у второго 70%. Для контроля в магазине взято наугад одно изделие. Какова вероятность того, что это окажутся мясные консервы?
Решение. Обозначим:
событие А – взяты мясные консервы;
событие Н1– консервы изготовлены I заводом;
событие Н2– консервы изготовлены II заводом.
По условию задачи первый завод поставляет 75% продукции, тогда Р(Н1) = 0,75, второй завод поставляет - 25%, следовательно Р(Н2) = 0,25. Вероятность того, что консервы мясные, для первого завода составляет 40%, то есть 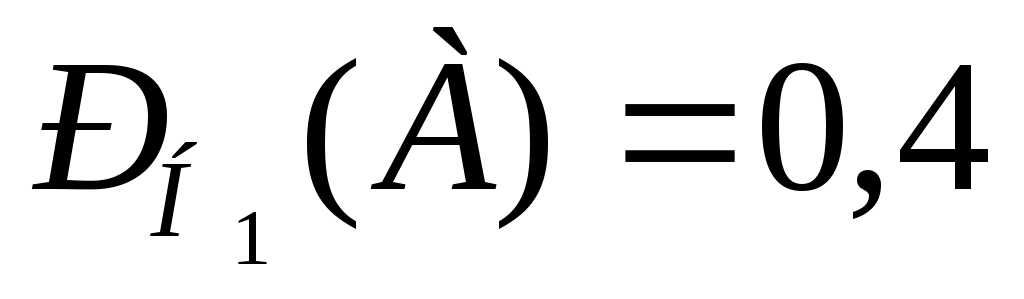 , для второго завода - 30%, то есть , для второго завода - 30%, то есть 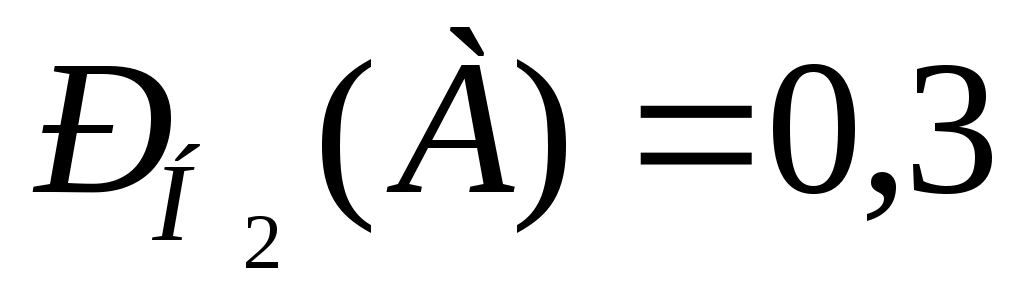 . Учитывая, что событие А произойдет обязательно с одним из событий (гипотез) Нi, образующих полную группу, применяем формулу полной вероятности: . Учитывая, что событие А произойдет обязательно с одним из событий (гипотез) Нi, образующих полную группу, применяем формулу полной вероятности:
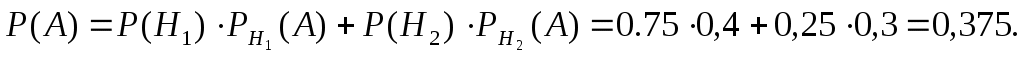
Замечание. Задача решается аналогично, если количество заводов будет три или более. Соответственно увеличится число слагаемых в формуле полной вероятности.
Задачи 81-90
Вероятность того, что в результате проверки изделию будет присвоен знак «изделие высшего качества» равна p. На контроль поступило n изделий. Какова вероятность того, что знак высшего качества будет присвоен:
а) ровно k изделиям;
б) более чем m изделиям;
в) хотя бы одному изделию;
г) указать наивероятнейшее количество изделий, получивших знак высшего качества, и найти соответствующую ему вероятность.
81. n=8; p=0,4; k=5; m=6.
82. n=7; p=0,3; k=4; m=5.
83. n=6; p=0,2; k=3; m=4.
84. n=5; p=0,3; k=2; m=3.
85. n=4; p=0,6; k=1; m=2.
86. n=9; p=0,2; k=6; m=7.
87. n=7; p=0,7; k=3; m=4.
88. n=6; p=0,4; k=1; m=3.
89. n=8; p=0,6; k=4; m=5.
90. n=5; p=0,5; k=3; m=2.
Методические указания к решению задач 81 – 90
Повторение независимых испытаний
Пусть известна вероятность появления события А в каждом испытании: Р(А) = р, тогда  1 – p = q – вероятность не появления события А. Испытание повторяется n раз. Требуется найти вероятность того, что событие А наступит при этом ровно k раз. 1 – p = q – вероятность не появления события А. Испытание повторяется n раз. Требуется найти вероятность того, что событие А наступит при этом ровно k раз.
Обозначим Рn(k) – вероятность того, что в n испытаниях событие А наступит k раз. Эта вероятность находится по формуле Бернулли:
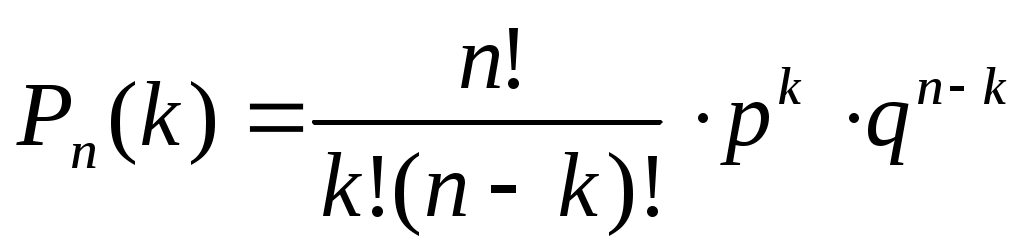 , ,
! - знак факториала, математической операции такой, что
n! = 1 2 3 … n. Например, 1! = 1
2! = 12=2
Внимание: 0!=1 3! = 123=6
4! = 1234=24
5! = 12345=120 и т. д.
Наивероятнейшее число появлений события
Пусть в n повторных испытаниях событие А появляется kраз, где k может принимать значения: 0; 1; 2; …; n (то есть 0 kn). Для каждого из этих значений k можно найти соответствующую ему вероятность по формуле Бернулли.
Значение k, которому соответствует самая большая вероятность, называется наивероятнейшимчислом появления события А.
Наивероятнейшее число k0 находится как целое число из промежутка:
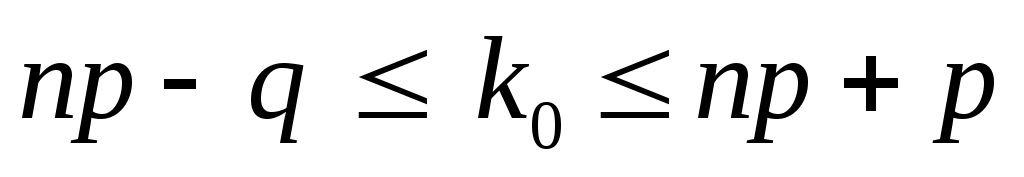 . .
При этомk0 может принимать либо одно значение, либо два соседних целых значения с одинаковой вероятностью.
Вероятность Рn(kо), соответствующую значению k = k0, находим по формуле Бернулли.
Появление события хотя бы один раз
Вероятность появления события «хотя бы один раз» в n испытаниях находится с помощью противоположного ему события «ни одного раза»:
Рn(событие наступит хотя бы один раз) = 1 – Рn (ни разу) 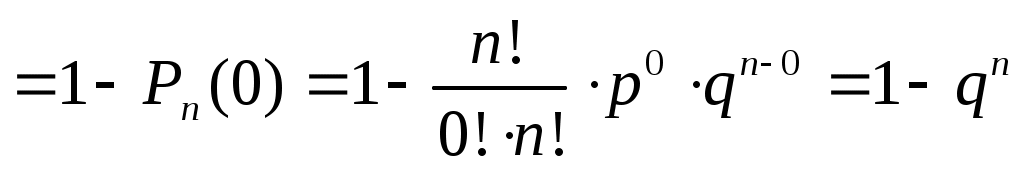 , ,
при этом учтено, что 0! = 1 и 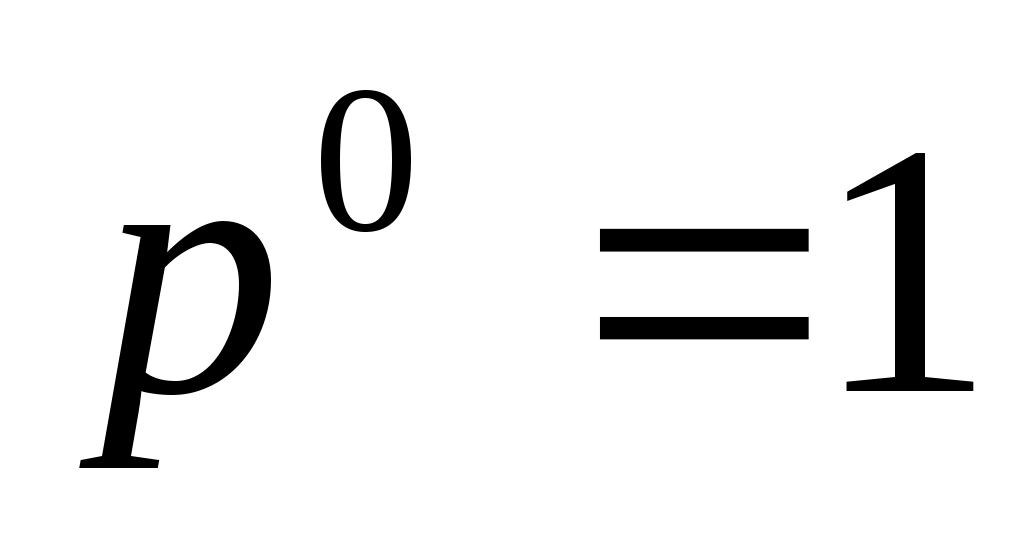 . .
Событие наступит «хотя бы один раз» означает, что оно наступит один или более раз, поэтому можно записать:
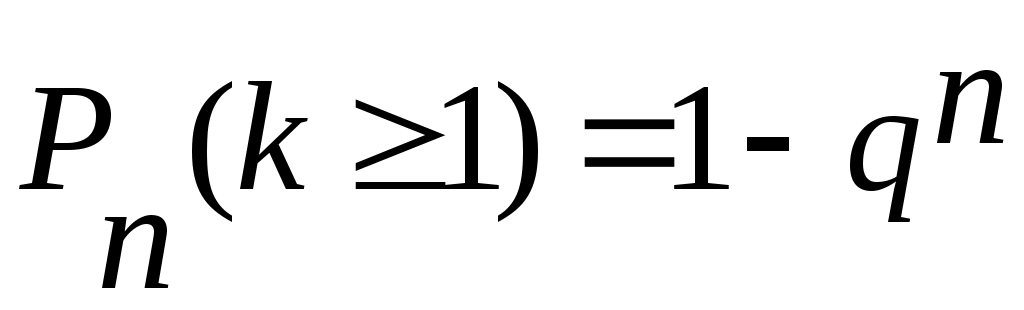 . .
Задача. Стрелок поражает цель с вероятностью 0,7. С какой вероятностью в серии из 5 выстрелов он поразит мишень:
а) ровно два раза;
б) более трех раз;
в) хотя бы один раз;
г ) указать наивероятнейшее число попаданий и соответствующую ему вероятность.
Решение. По условию задачи: р = 0,7; n = 5; k = 2; m = 3;
вероятность промаха q = 1 - р = 1 - 0,7 = 0,3.
а) Вероятность попадания ровно два раза в серии из пяти выстрелов находим по формуле Бернулли:
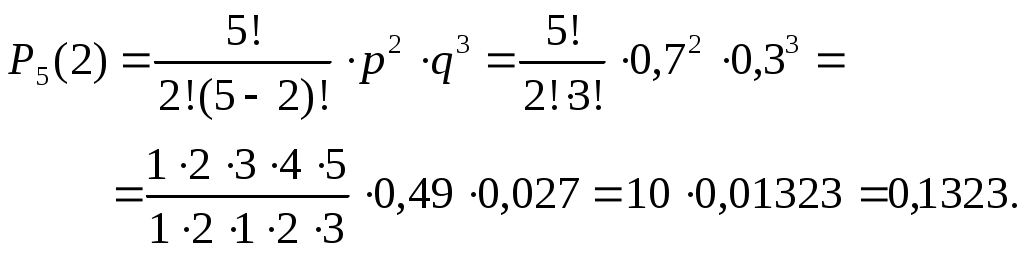
б) Событие «стрелок поразит мишень более трех раз» запишем в виде: m > 3, тогда
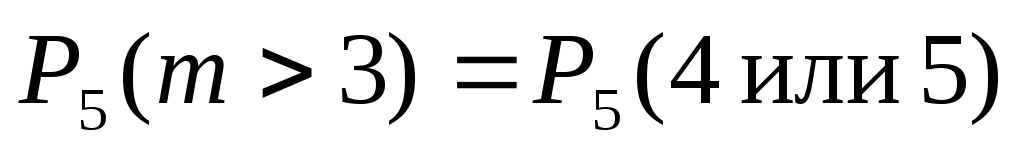 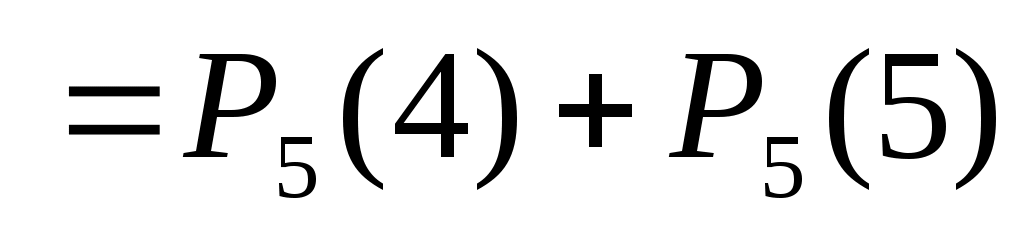 . .
Здесь применена теорема сложения вероятностей несовместных событий. Используя формулу Бернулли, найдем:
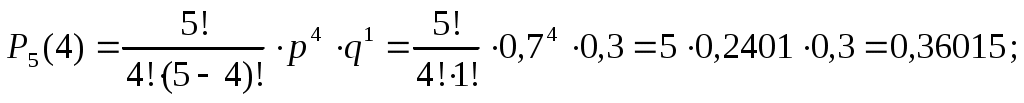 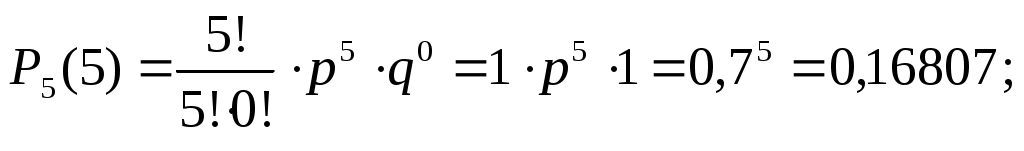
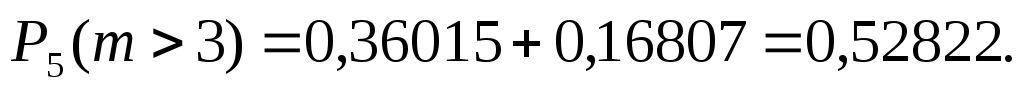
в) Событию D – «стрелок поразит мишень хотя бы 1 раз», противоположно событие 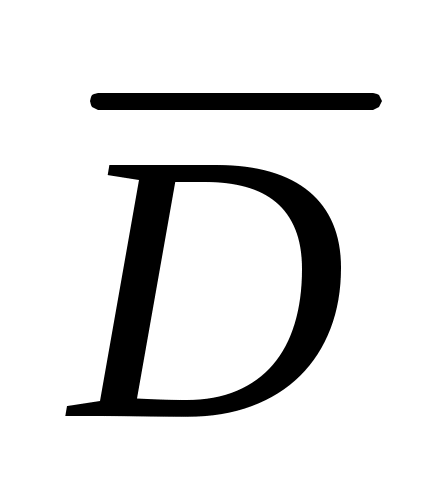 - «не поразит ни разу», то есть стрелок промахнется все пять раз, следовательно, число попаданий k = 0: - «не поразит ни разу», то есть стрелок промахнется все пять раз, следовательно, число попаданий k = 0:
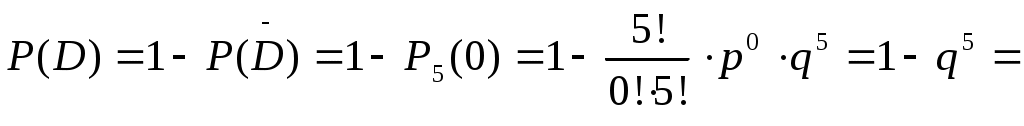
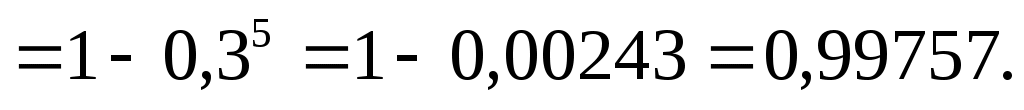
Здесь учтено, что 0! = 1 и 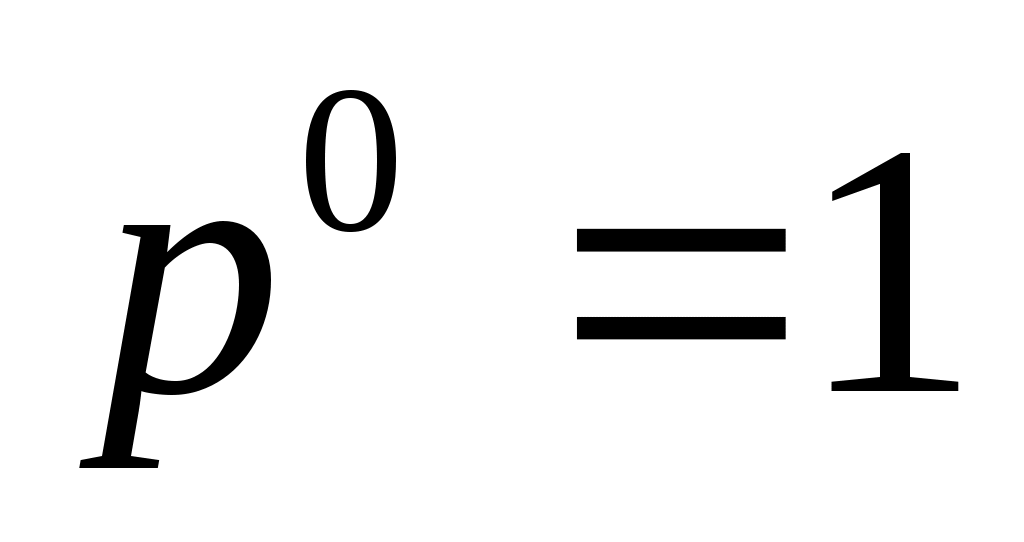 . .
г) Наивероятнейшее число попаданий kо находим как целое число из промежутка:
nр – q kоnр + р ;
5 0,7 – 0,3 kо 5 0,7 + 0,7 ;
3,2 kо4,2 ;
kо= 4 .
Соответствующую ему вероятность 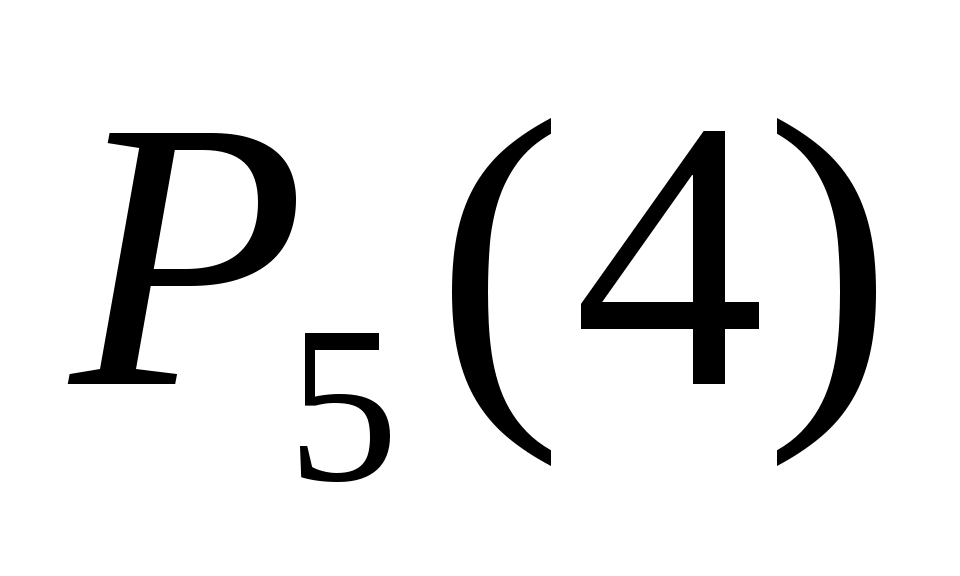 вычислим по формуле Бернулли. В данной задаче она уже была найдена выше: вычислим по формуле Бернулли. В данной задаче она уже была найдена выше:
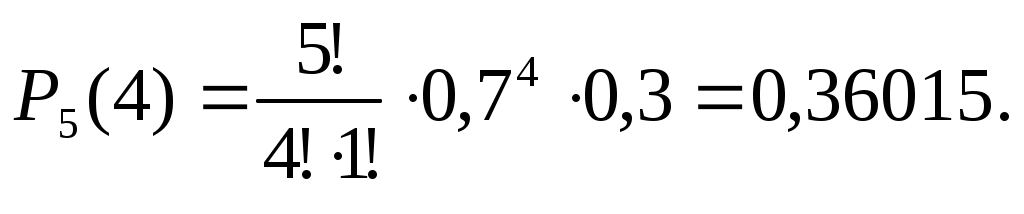
Задачи 91-100
В рекламных целях торговая фирма вкладывает в свой товар случайным образом некоторые призы. На каждые 100 единиц товара приходится m1 призов стоимостью a1рублей, m2 призов стоимостью a2 рублей, m3 призов стоимостью a3 рублей и т. д. В остальных единицах товара призов нет.
Составить закон распределения величины стоимости приза для человека, купившего одну единицу товара этой фирмы и найти его основные характеристики: математическое ожидание, дисперсию (двумя способами) и среднее квадратическое отклонение. Пояснить смысл полученных результатов.
91. а1=20; а2=10; а3= 5; а4= 3;
m1=1; m2=2; m3=8; m4=10.
92. а1=18; а2=15; а3=10; а4=35;
m1=2; m2=3; m3=5; m4=20.
93. а1=15; а2=12; а3= 8; а4= 4;
m1=3; m2=10; m3=15; m4=20.
94. а1=16; а2=10; а3= 6; а4= 3;
m1=2; m2=5; m3=8; m4=10.
95. а1=10; а2= 8; а3= 6; а4= 4;
m1=5; m2=10; m3=12; m4=15.
96. а1=6; а2=5; а3= 4; а4= 3;
m1=2; m2=4; m3=6; m4=10.
97. а1=14; а2=12; а3= 8; а4= 5;
m1=2; m2=8; m3=15; m4=20.
98. а1=12; а2=10; а3= 6; а4= 3;
m1=5; m2=8 m3=14; m4=25.
99. а1=8; а2=5; а3= 4; а4= 2;
m1=4; m2=6; m3=12; m4=20.
100. а1=5; а2=4; а3= 3; а4= 2;
m1=8; m2=10; m3=15; m4=25.
Методические указания к решению задач 91 – 100
Основные характеристики дискретной случайной величины
Случайной величиной называется переменная, принимающая свои возможные числовые значения с определенной вероятностью.
Например: Х – балл, полученный на экзамене;
Y – число студентов, явившихся на лекцию;
Z – величина выигрыша в лотерее;
U – рост случайно выбранного человека и т.п.
Дискретная случайная величина Х принимает отдельные числовые значения. Закон распределения дискретной случайной величины записывается в виде таблицы, где перечислены все значения случайной величины Х и соответствующие им вероятности:
Х
|
х1
|
х2
|
х3
|
…
|
хn
|
Р(Х)
|
р1
|
р2
|
р3
|
…
|
рn
|
Следует иметь в виду, что всегда 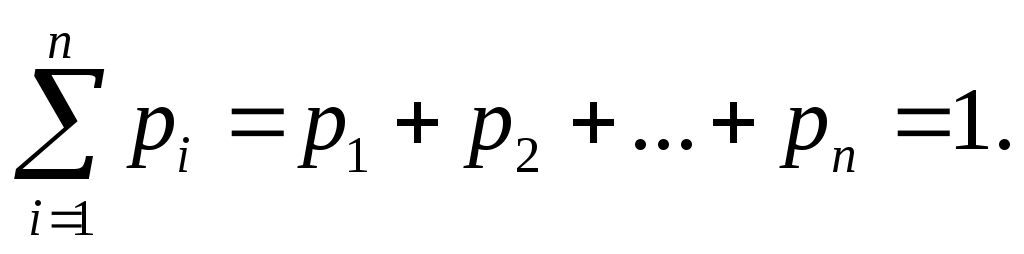
Основные числовые характеристики закона распределения дискретной случайной величины:
1) Математическое ожидание (ожидаемое среднее значение случайной величины)
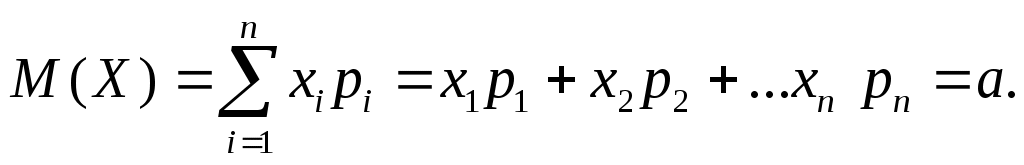
2) Дисперсия (мера рассеяния значений случайной величины Х от среднего значения а):
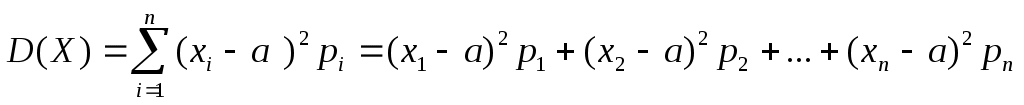 . .
Второй способ вычисления дисперсии:
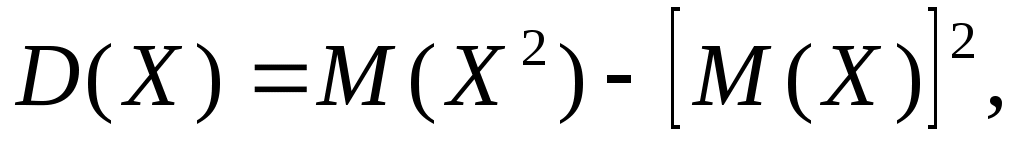
где M(X) определено выше, а
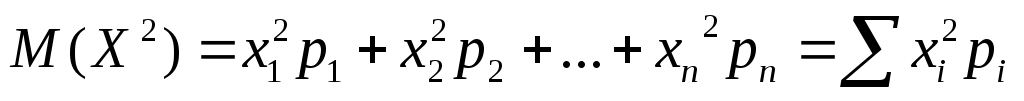 . .
3) Среднее квадратическое отклонение (характеристика рассеяния в единицах признака Х):
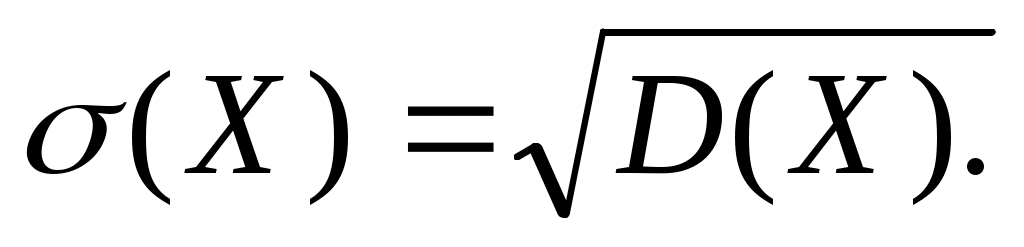
Задача. В лотерее на каждые 100 билетов приходится 2 билета с выигрышем по 50 тыс. рублей, 5 билетов по 20 тыс. рублей, 10 билетов по 10 тыс. рублей, 20 билетов по 5 тыс. рублей и 25 билетов по 3 тыс. рублей. Остальные билеты не выигрывают. Составить закон распределения величины выигрыша для владельца одного билета и найти его основные характеристики.
Решение. Обозначим X тыс. рублей – величина выигрыша на один билет. Очевидно, что X – случайная дискретная величина. Составим закон распределения этой случайной величины, перечислив все ее возможные значения и найдя соответствующие им вероятности. Число выигрышных билетов из 100 составляет: 2+5+10+20+25=62, значит, число невыигрышных билетов: 100 – 62 = 38.
Располагая величины возможного выигрыша xiв порядке возрастания, получим следующую таблицу:
xi
|
0
|
3
|
5
|
10
|
20
|
50
|
pi
|
0,38
|
0,25
|
0,20
|
0,10
|
0,05
|
0,02
|
где 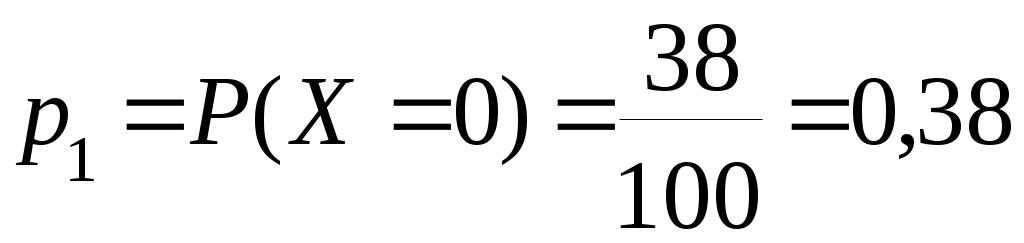 ; ; 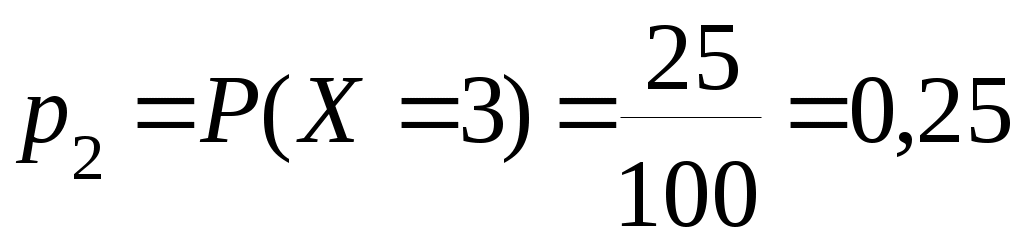 и т. д. и т. д.
Отметим, что 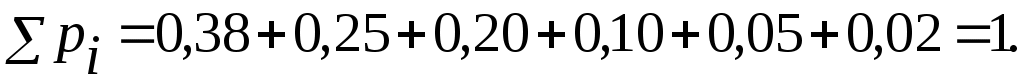
1) Математическое ожидание случайной величины X:
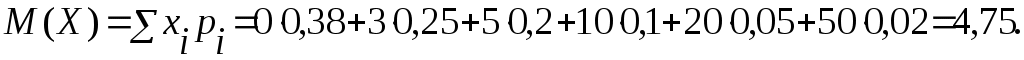
Таким образом, ожидаемый средний выигрыш на 1 билет составляет 4,75 тыс. рублей.
2) Дисперсию случайной величины найдем двумя способами:
1).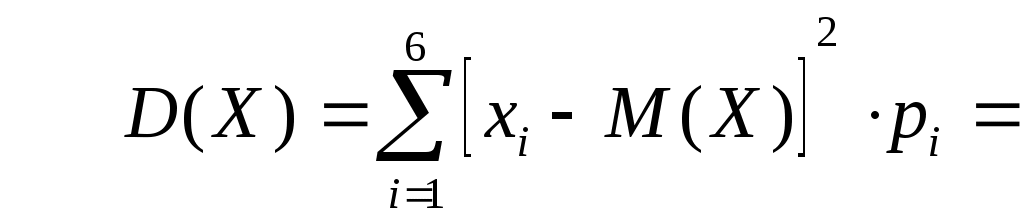
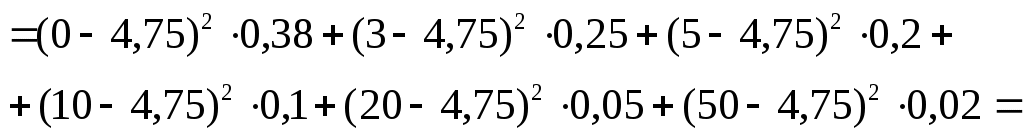
=8,57375+0,76525+0,0125+2,75625+11,628125+40,95125=64,6875.
2). 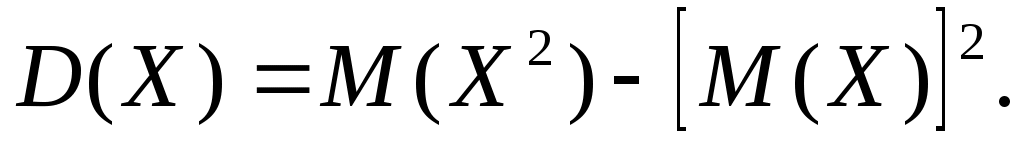
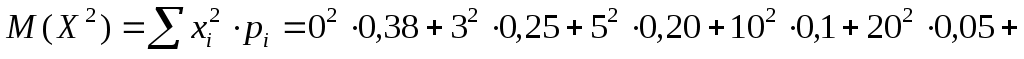 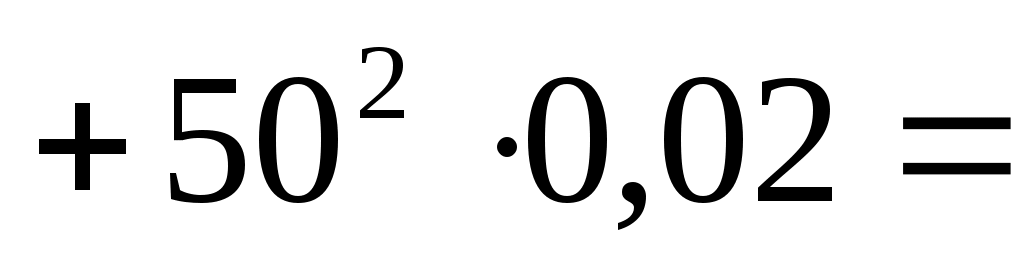 0+2,25+5+10+20+50 = 87,25. 0+2,25+5+10+20+50 = 87,25.
Тогда:
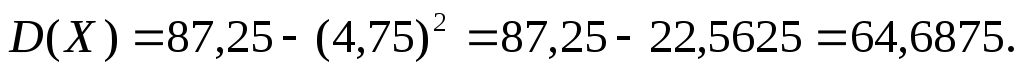
Результаты вычислений дисперсии по обоим способам совпадают.
3) Среднее квадратичное отклонение:
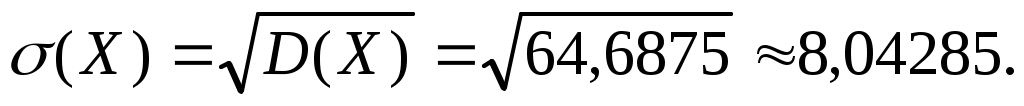
Таким образом, = 8,04285 тыс. рублей – характеристика разброса фактических значений выигрыша от найденного среднего значения а = 4,75 тыс. рублей. Это означает, что основные значения случайной величины выигрыша находятся в диапазоне 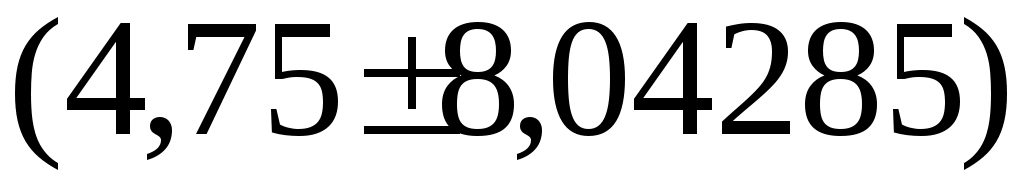 тыс. рублей, что соответствует таблице данных. тыс. рублей, что соответствует таблице данных.
|
 Скачать 2.28 Mb.
Скачать 2.28 Mb.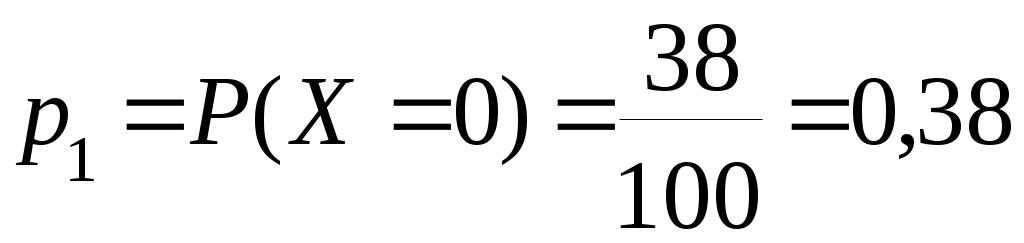 ;
; 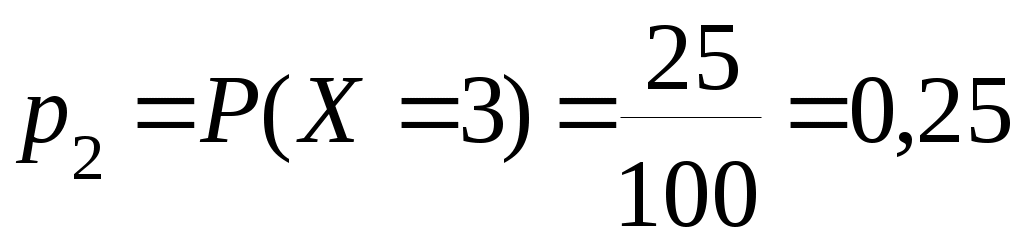 и т. д.
и т. д. 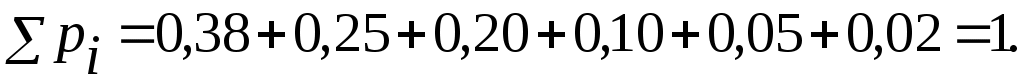

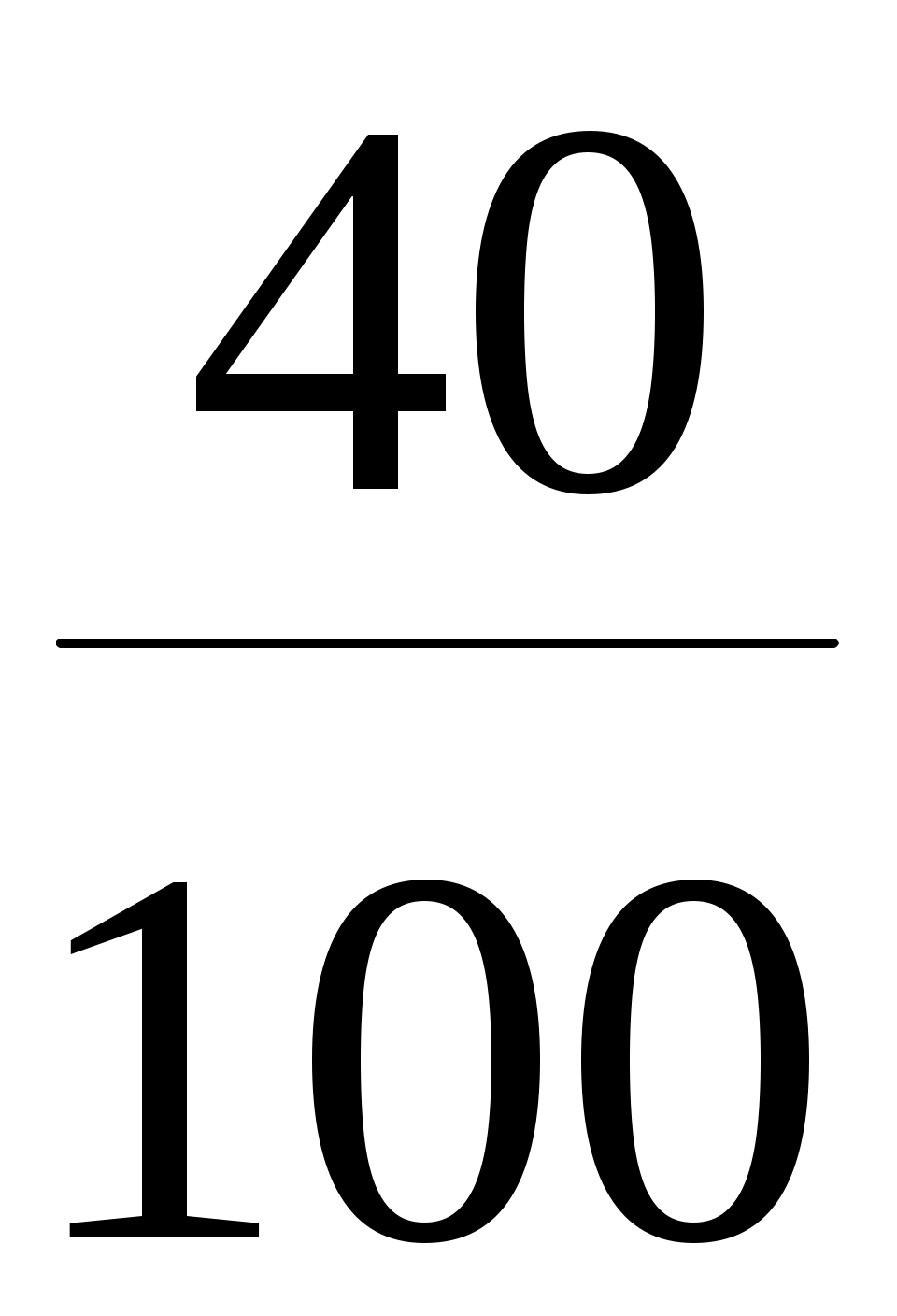 .
. 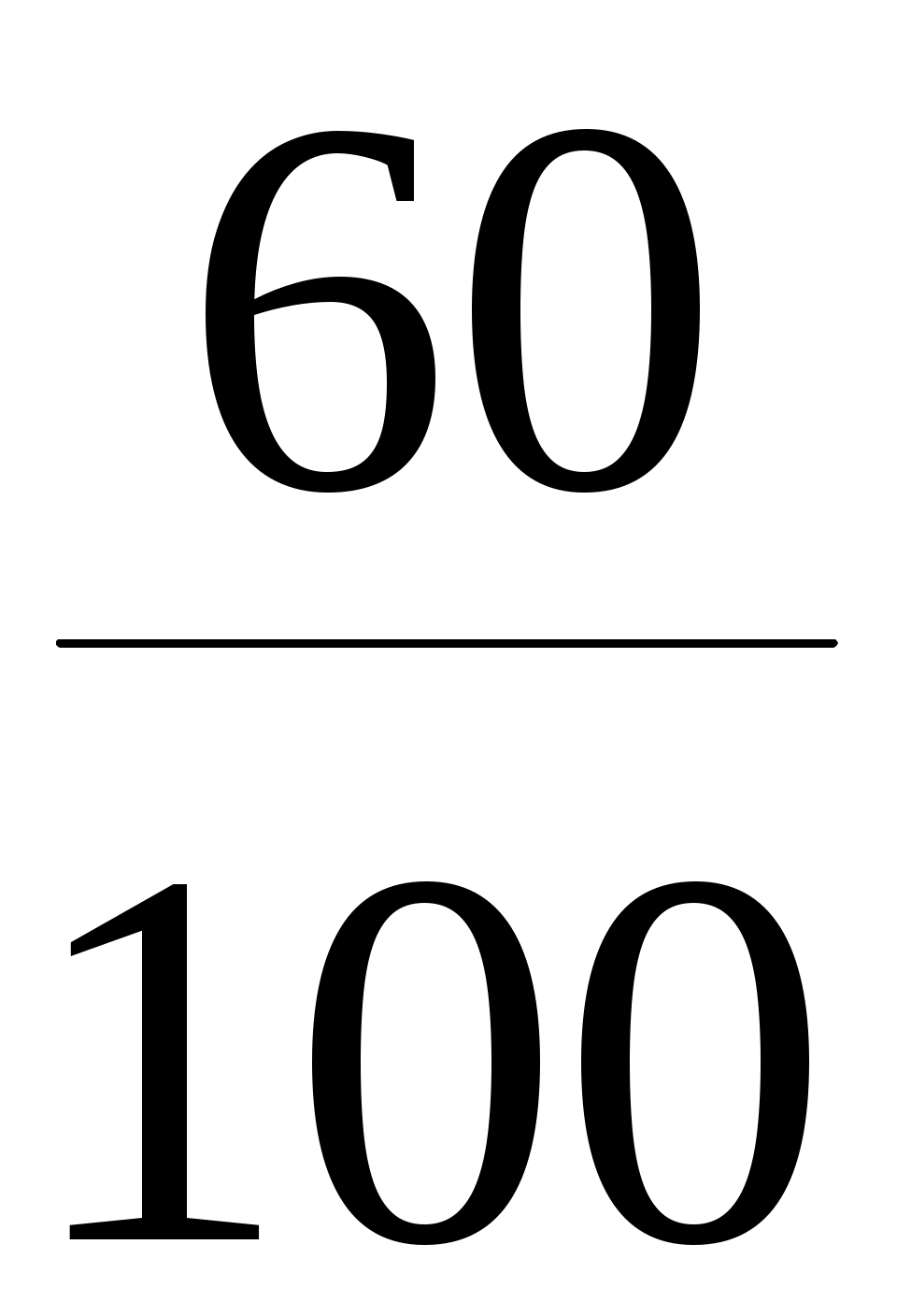 +
+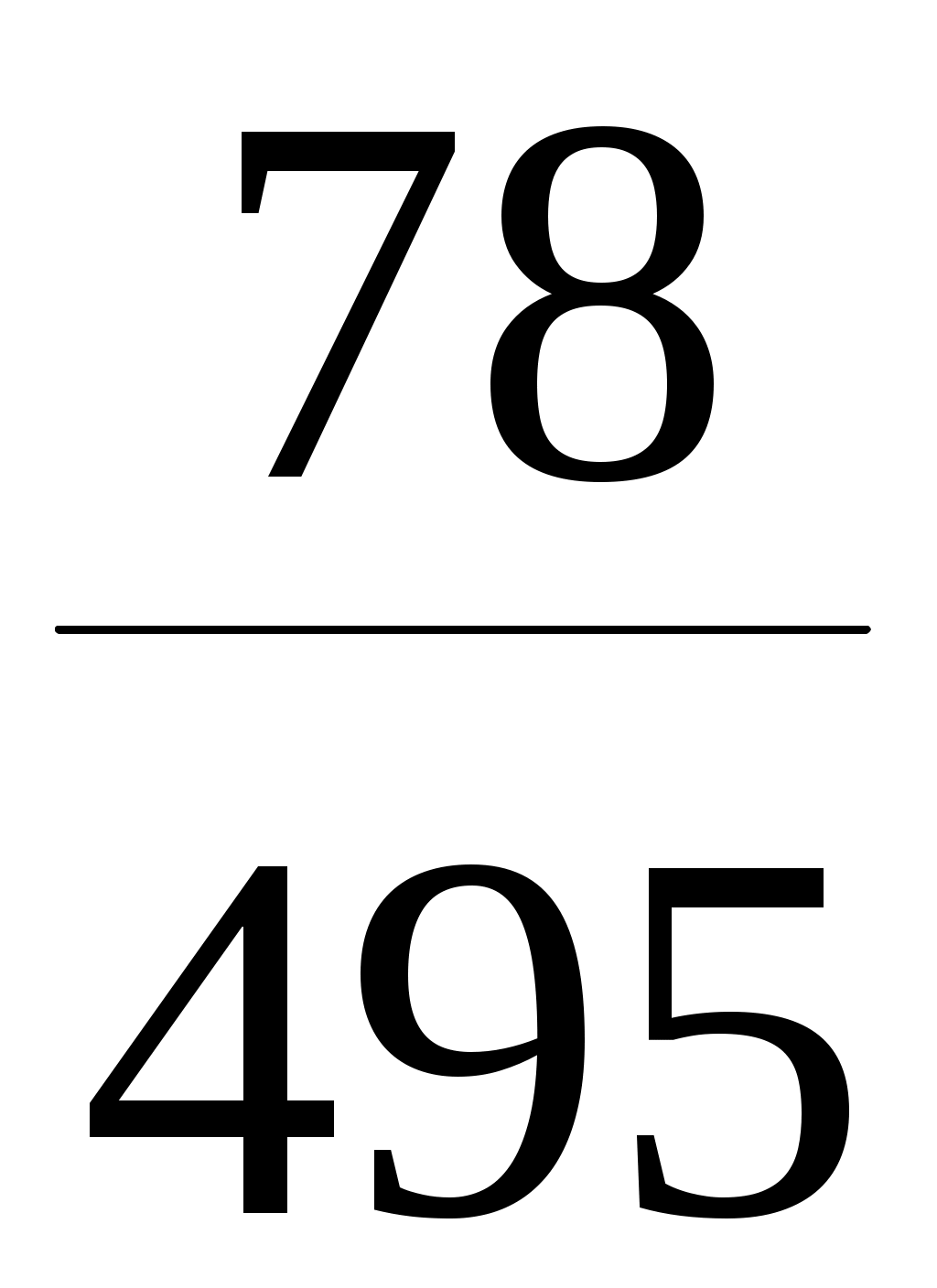 .
.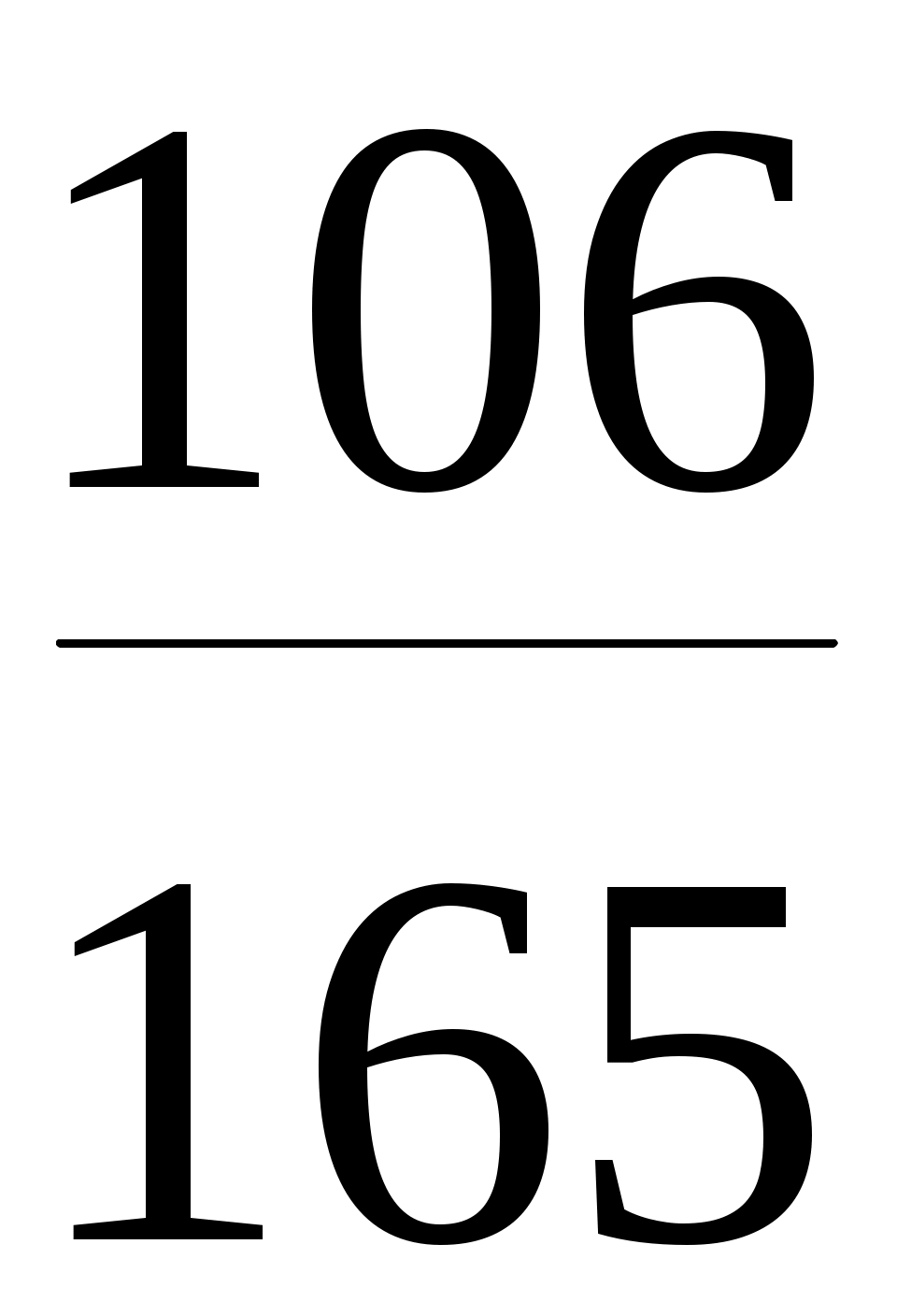 .
.