Математика. Б1.Б.11_ММ Математика 38.03.02. Методические указания и задания к занятиям семинарского типа, контрольной и самостоятельной работе по дисциплине математика
 Скачать 2.28 Mb. Скачать 2.28 Mb.
|
|
Тема 4. Интегральное исчисление и его приложения Основные вопросы. Определённый интеграл, его геометрический смысл. Основные методы интегрирования. Типовые задачи. 1. Найти неопределенные интегралы. Результаты проверить дифференцированием. а) г) 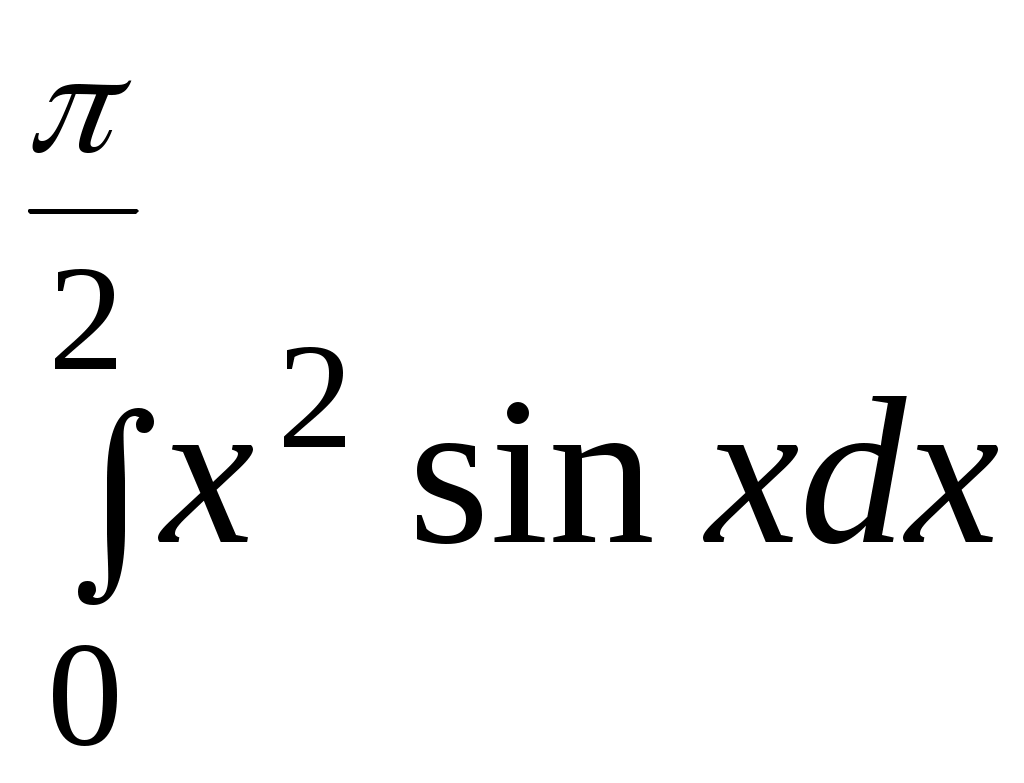 ; е) ; е) 2. Вычислить площади фигур, ограниченных линиями. Сделать чертеж.
Тема 5. Дифференциальные уравнения Основные вопросы. Понятие дифференциального уравнения и его порядка. Задача Коши для дифференциальных уравнений первого и второго порядков. Общее и частное решение дифференциального уравнения. Структура общего решения неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами. Типовые задачи. 1. Найти решение задачи Коши для дифференциального уравнения с разделяющимися переменными: 2. Найти общее решение и частное решение, удовлетворяющее начальному условию, для следующих линейных уравнений: а) 3. Найти общее решение и решение задачи Коши для однородных линейных ДУ с постоянными коэффициентами: Тема 6. Аналитическая геометрия в пространстве Основные вопросы. Линейные операции над векторами, заданными геометрически и в координатной форме. Скалярное произведение векторов. Понятие векторного произведения векторов, его вычисление в координатной форме. Условия коллинеарности и ортогональности векторов. Общее уравнение плоскости в пространстве. Его частные случаи. Общие и канонические уравнения прямой в пространстве. Типовые задачи. 1. Найти вектор 4a– 3b, если а = 2i -5j, b = -i +4j. 2. Найти скалярное и векторное произведения векторов: 3. Найти параметр tтак, чтобы векторы a = -6i +7j -tk и b = ti -2j +k были ортогональны. 4. Найти угол между векторами 5. Составить уравнение плоскости, проходящей через точку 6. Составить уравнение прямой, проходящей через точку 7. Составить уравнение прямой, проходящей через две точки А(3;2;1) и В(0;2;5). 8. Найти точку пересечения прямой 9. Найти уравнение плоскости, проходящей через три заданные точки: М1(3; -1;5), М2(-2;1;4) и М3(0;-3;6). Тема 7. Функции нескольких переменных Основные вопросы. Понятие функции двух переменных, её графическое изображение. Линии уровня для функции двух переменных. Понятие частных производных, их смысл. Полный дифференциал для функции двух и трёх переменных. Производная по направлению, её смысл. Вектор-градиент, его смысл. Понятие экстремума для функции двух переменных, необходимые и достаточные условия существования экстремума. Типовые задачи. 1. Найти уравнение линий уровня и построить несколько линий уровня для функции: а) z = х – 2у; б) z = ху. 2. Найти частные производные а) 3. Найти градиент функции 4. Найти производную функции 5. Найти экстремум функции во всей её области определения: 6. Найти наибольшее и наименьшее значения функции 7. Найти наибольшее и наименьшее значения функции Тема 8. Матрицы Основные вопросы. Векторное пространство Rn. Матрицы, действия над матрицами. Определители. Свойства определителей. Обратная матрица. Типовые задачи. 1. Вычислить определители: а)  , б) , б) 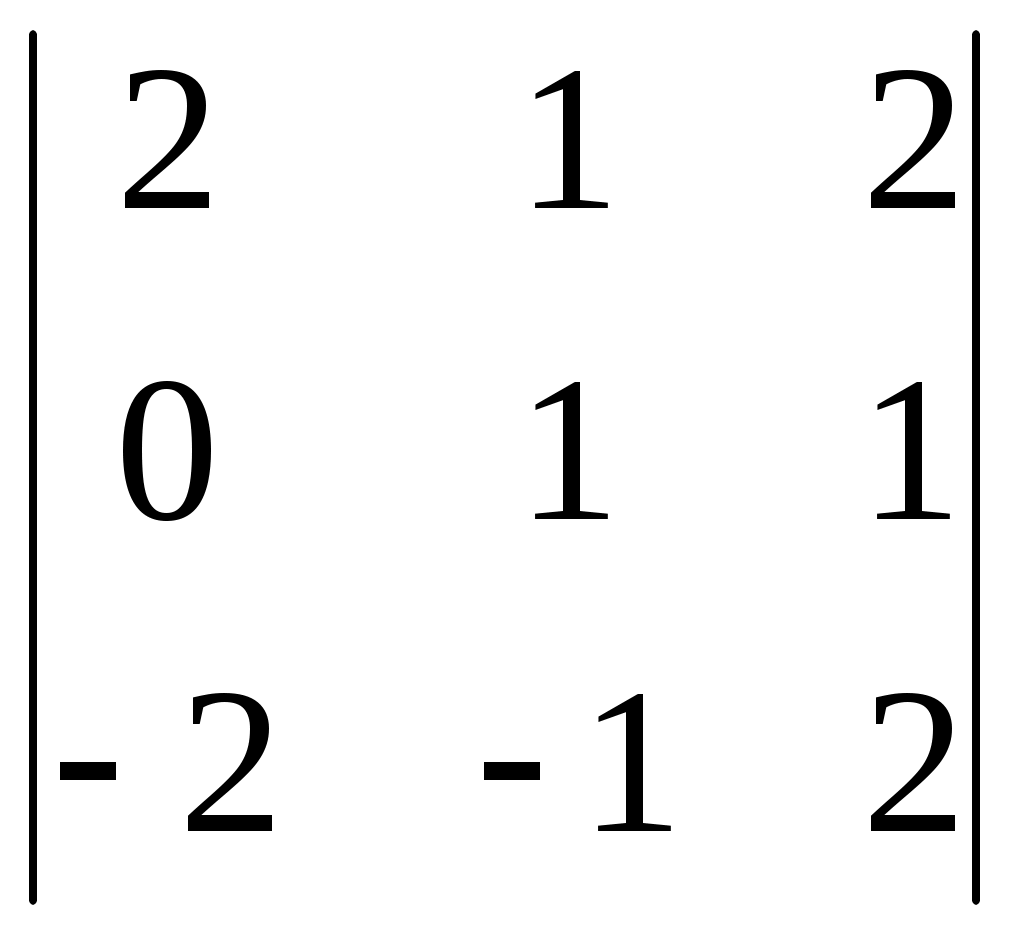 , с) , с) 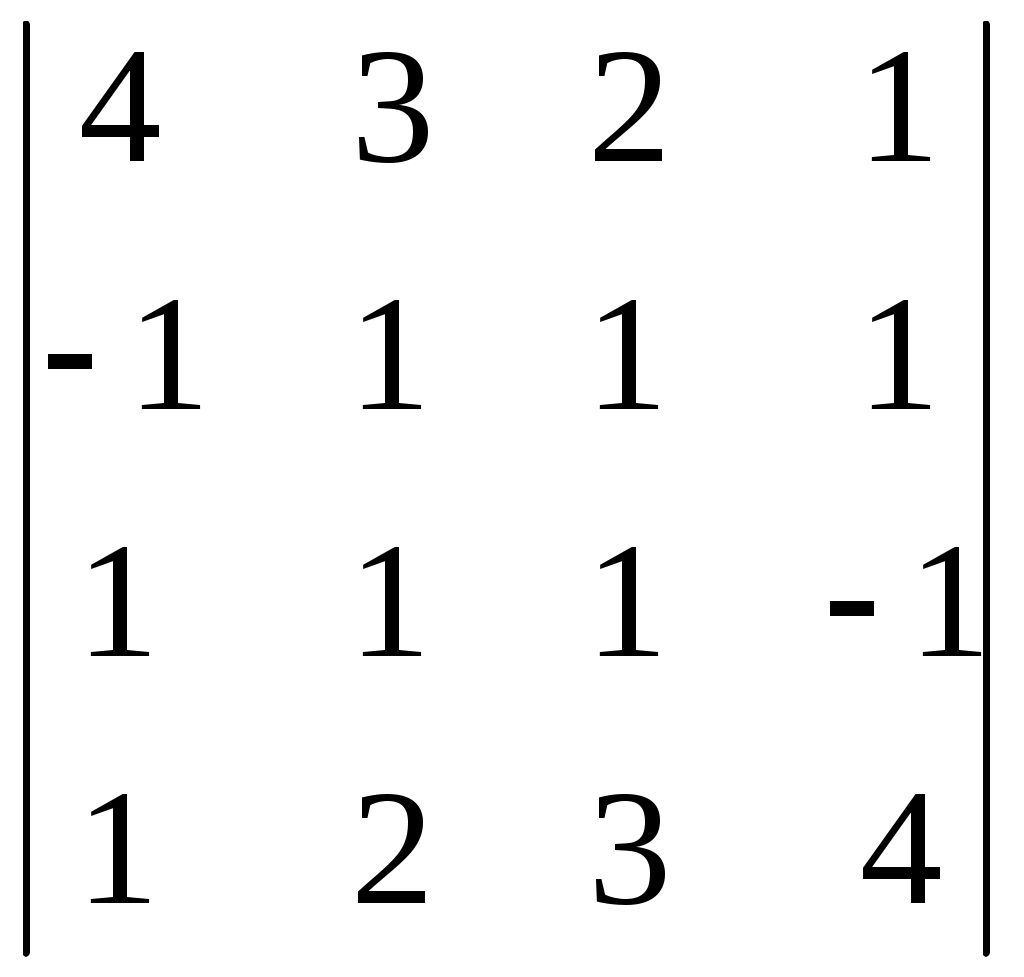 2. Вычислить обратную матрицу и сделать проверку: а) 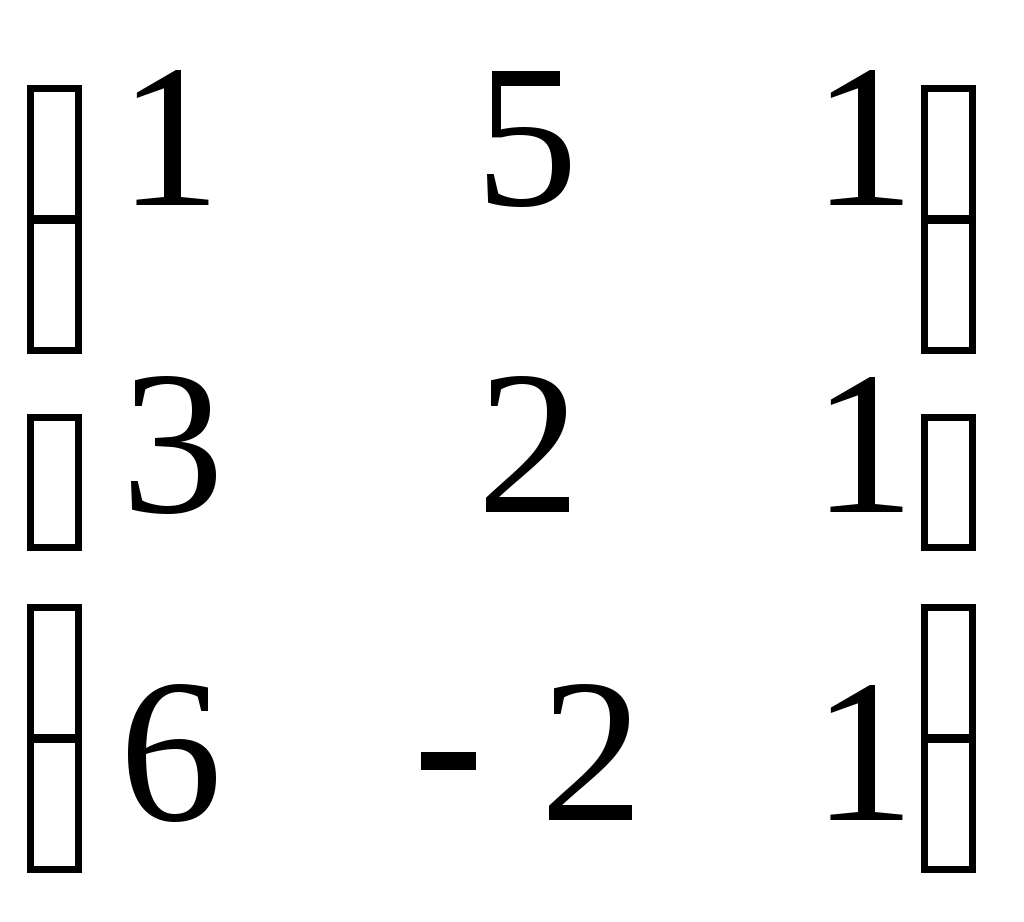 , б) , б)  , с) , с) 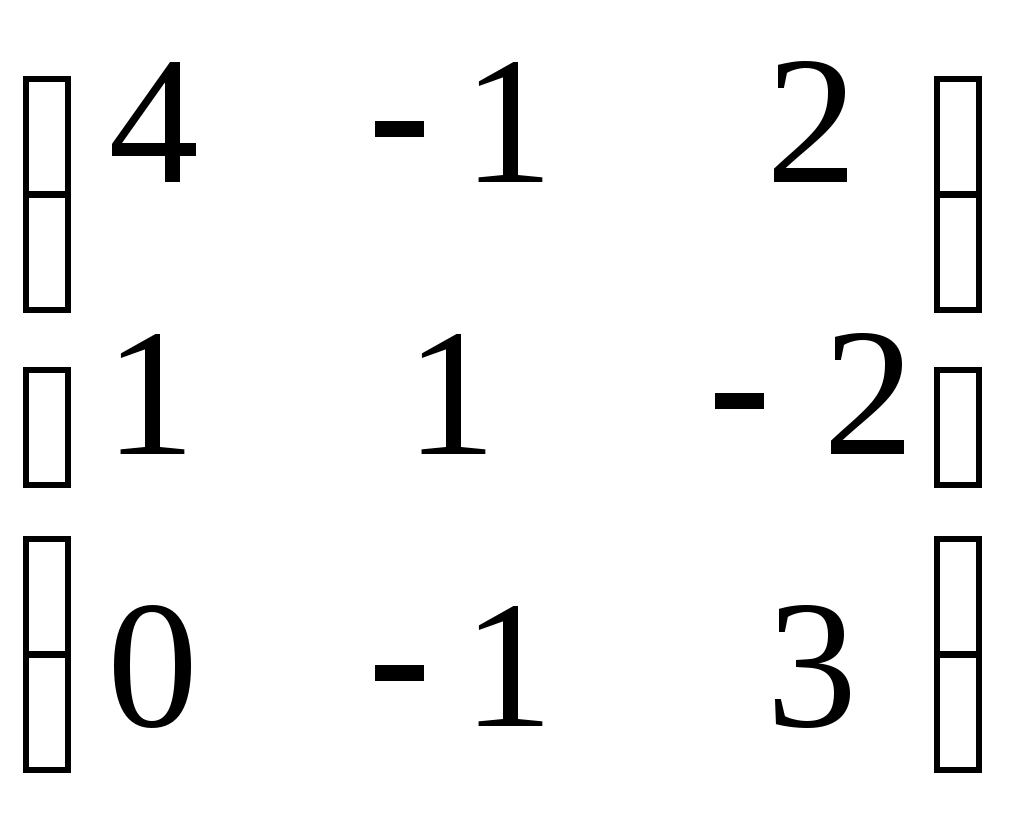 Тема 9. Система линейных алгебраических уравнений Основные вопросы. Решение СЛАУ методом исключения Жордана-Гаусса. Решение СЛАУ методом Крамера и обратной матрицы. Решение однородных систем алгебраических уравнений. Фундаментальная система решений СЛАУ. Типовые задачи. 1. Решить систему уравнений: а) 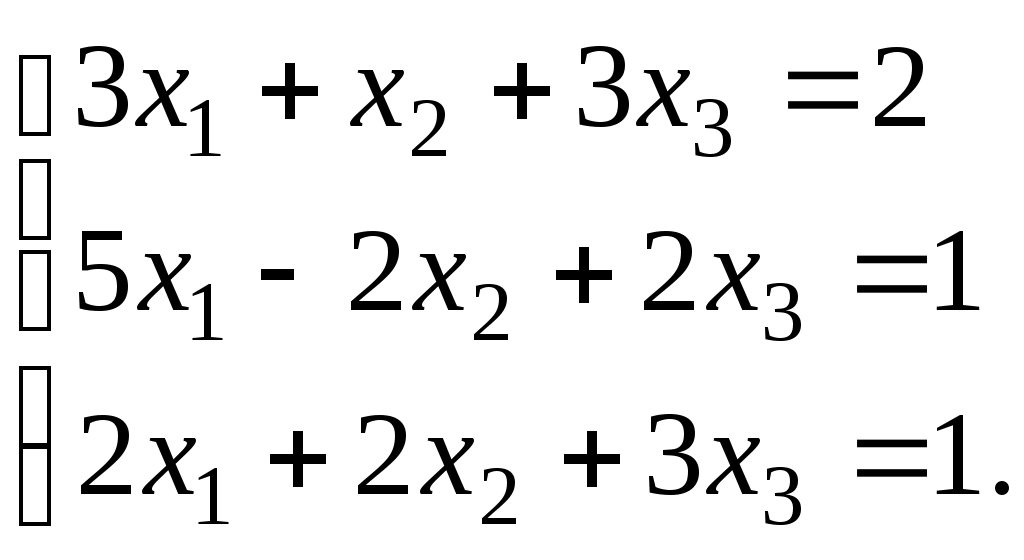 б) б) 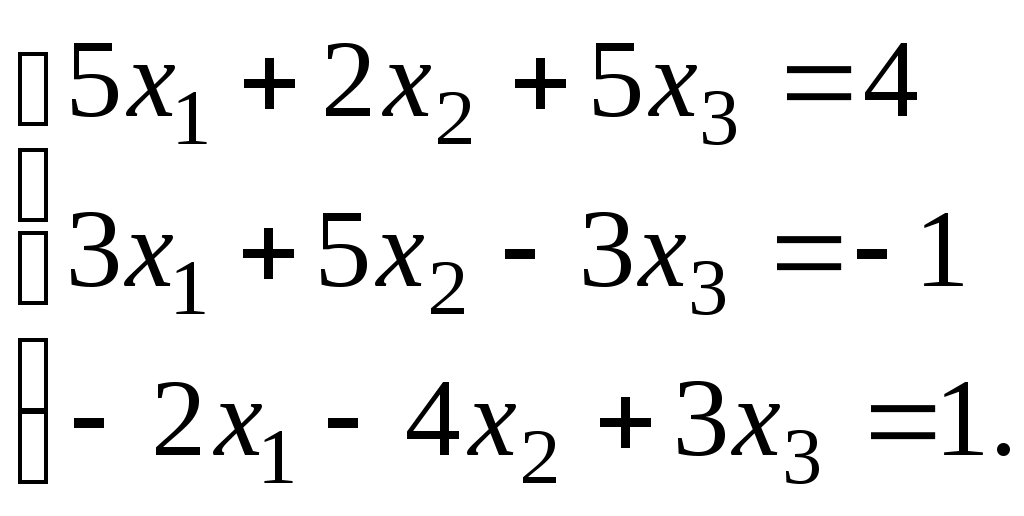 2. Исследовать совместность системы уравнений и в случае совместности найти её общее решение: а) 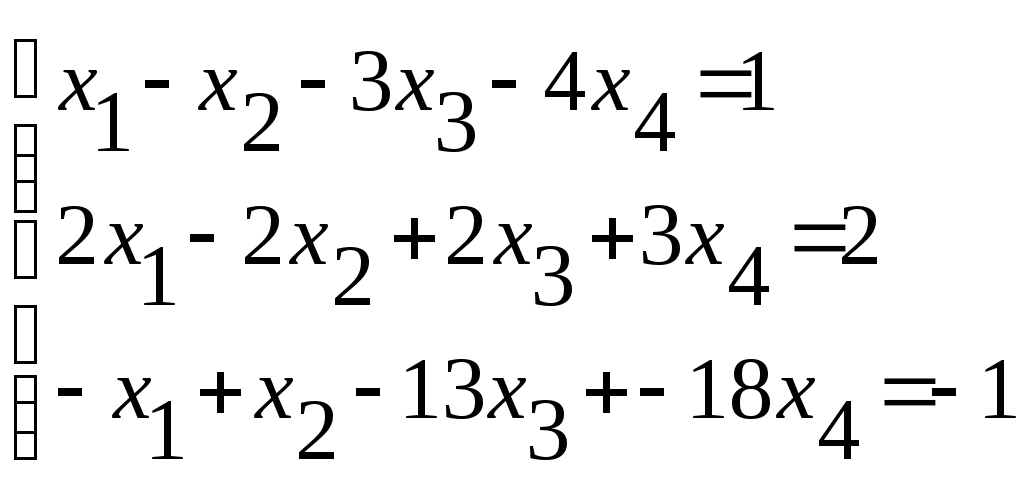 б) б) 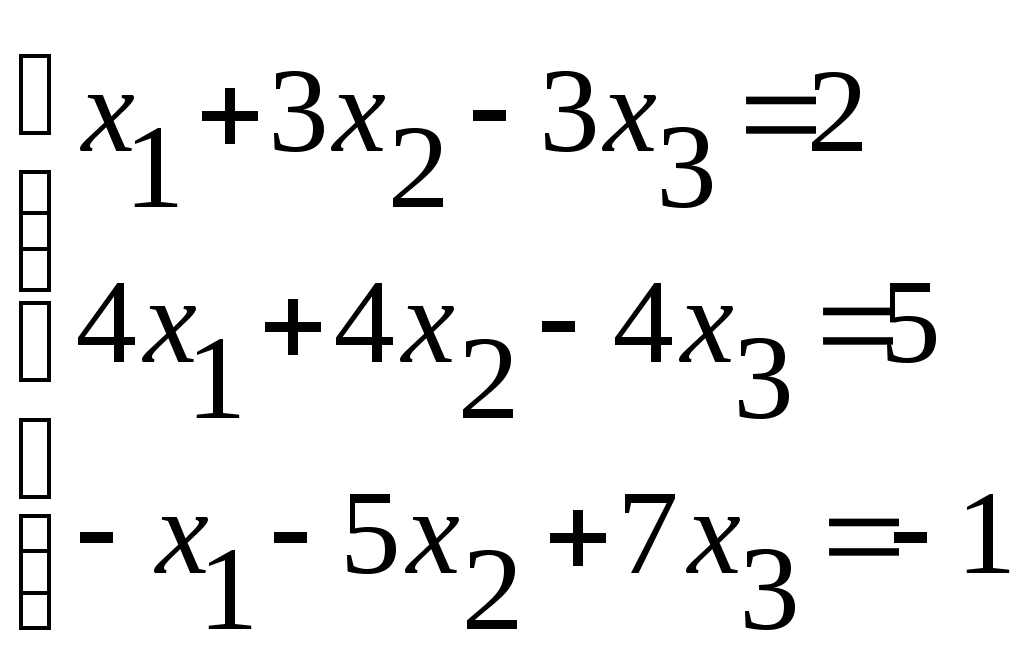 Тема 10. Задачи линейного программирования Основные вопросы. Постановка задачи линейного программирования (ЛП). Выпуклые многогранники в Rn. Геометрическая интерпретация решения задачи ЛП. Существование решения задачи ЛП. Задача ЛП как экстремальная задача функции нескольких переменных. Схема симплекс – метода. Типовые задачи. 1. Для изготовления компота двух видов используются яблоки, вишни, сливы. Количество фруктов в килограммах для изготовления одной банки компота и цена одной банки компота каждого вида даются в таблице:
Составить план производства, дающий максимальный доход от реализации продукции. 2. Решить графически задачу линейного программирования: 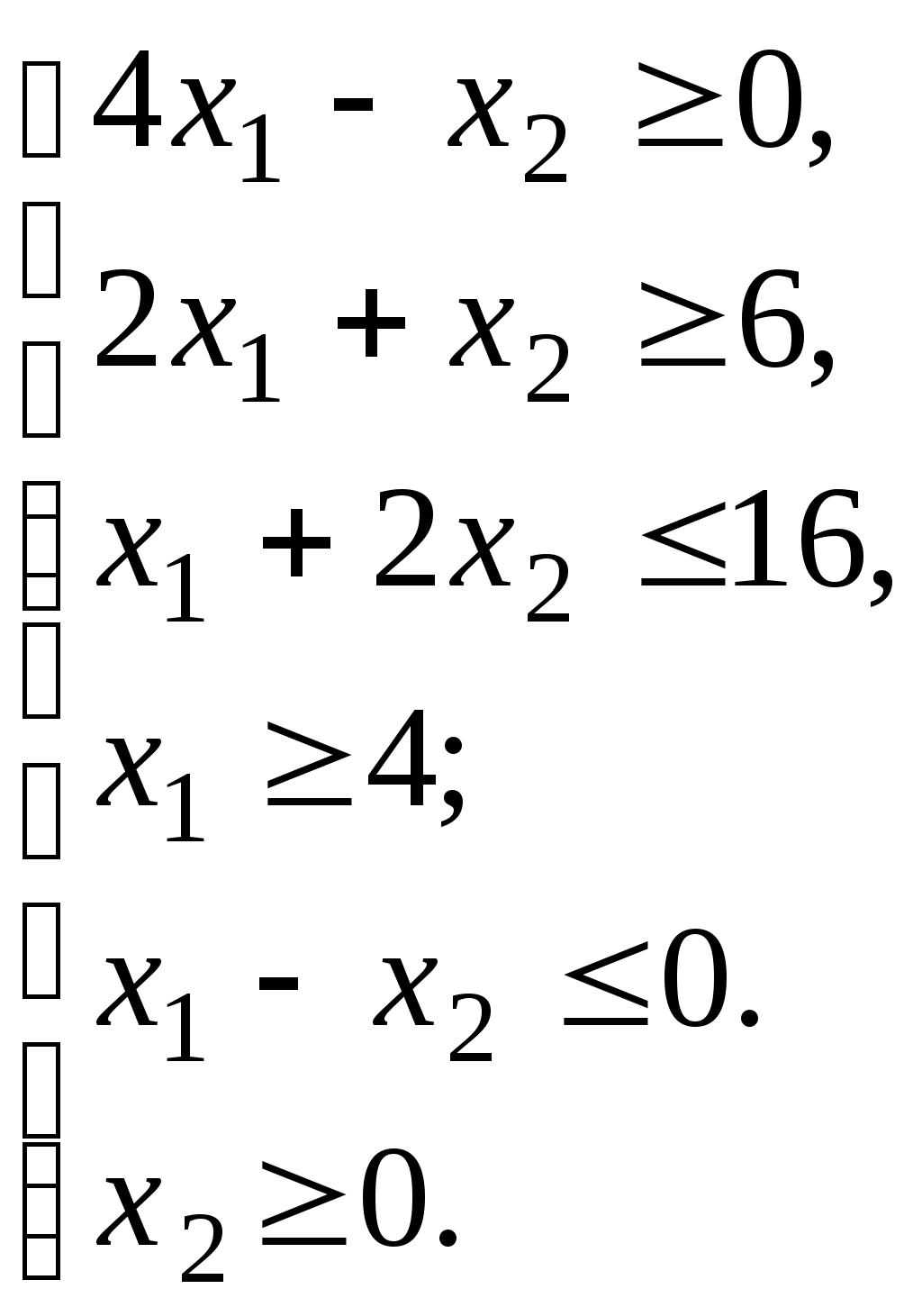 Тема 11. Транспортная задача линейного программирования Основные вопросы. Постановка транспортной задачи, сведение ее к задаче ЛП. Схема решения транспортной задачи. Типовые задачи. 1. На трех станциях А1, А2, А3 сосредоточен однородный груз соответственно в объемах 9,16,5 (т), который необходимо доставить четырем потребителям В1, В2, В3, В4 соответственно в объемах 11, 7, 8, 4 (т). Затраты на перевозку тонны груза из каждой станции до каждого потребителя заданы матрицей тарифов: 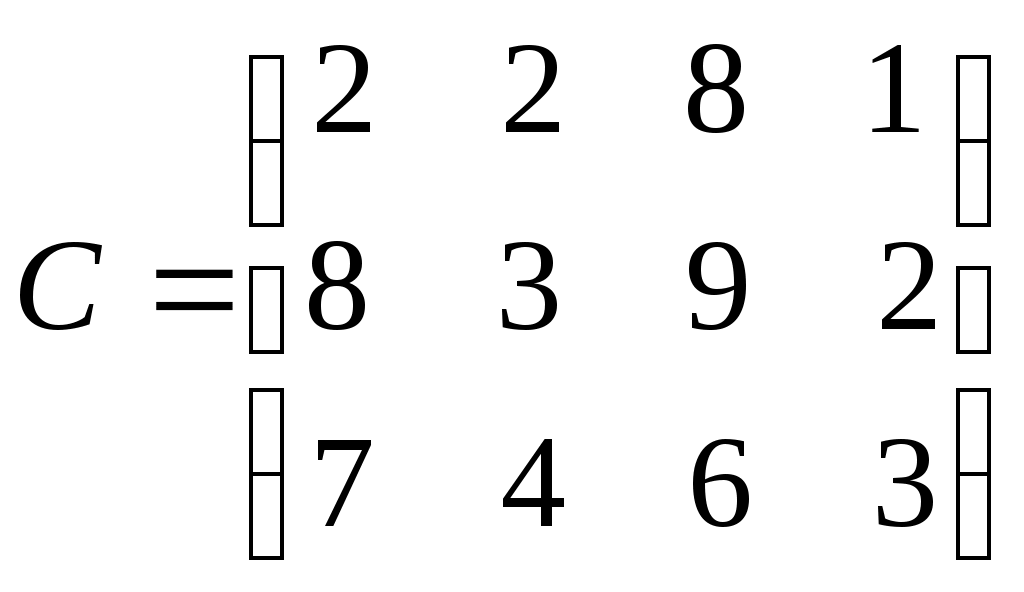 . .Требуется спланировать перевозки так, чтобы обеспечить минимум суммарных затрат на перевозку всех грузов. Тема 12. Оптимизационные задачи Основные вопросы. Экономические задачи, приводящие к задаче математического программирования. Построение математической модели. Задачи на безусловный экстремум, задача на условный экстремум, множители Лагранжа. Типовые задачи. Найти экстремумы функции f(x)= 2x1+4x2приусловии Имеется 3 механизма: А1, А2, А3, каждый из которых может быть использован на каждой из трёх видов работ: В1, В2, В3. Производительность их даётся в таблице
Требуется так распределить механизмы по видам работ, чтобы суммарная производительность была наибольшей, причём каждый механизм выполнял бы только один вид работ. Тема 13. Основные понятия и теоремы теории вероятностей Основные вопросы. Испытание, события, виды событий. Классическое и статистическое определения вероятности. Теоремы сложения вероятностей для несовместных и совместных событий. Теоремы умножения вероятностей для независимых и зависимых событий. Вероятность появления хотя бы одного события. Полная группа событий. Формула полной вероятности и формула Байеса. Типовые задачи. 1. Эксперт оценивает качественный уровень трех видов изделий по потребительским признакам. Вероятность того, что изделию первого вида будет присвоен знак качества, равна 0,95; для изделия второго вида эта вероятность равна 0,85; а для изделия третьего вида 0,65. Найти вероятность того, что знак качества будет присвоен: а) всем изделиям; б) только одному изделию; в) хотя бы одному изделию. 2. В партии товара, состоящей из 50 мужских костюмов, находится 30 изделий местного производства. Товаровед наудачу отбирает три изделия. Какова вероятность, что все три изделия окажутся: а) местного производства; б) не местного производства? | ||||||||||||||||||||||||||||||||||||||||||||||||||
