Математика. Б1.Б.11_ММ Математика 38.03.02. Методические указания и задания к занятиям семинарского типа, контрольной и самостоятельной работе по дисциплине математика
 Скачать 2.28 Mb. Скачать 2.28 Mb.
|
Линейная алгебраЗадачи 101–110 Показать, что система линейных уравнений имеет единственное решение, и найти его матричным способом. Сделать проверку. 101. 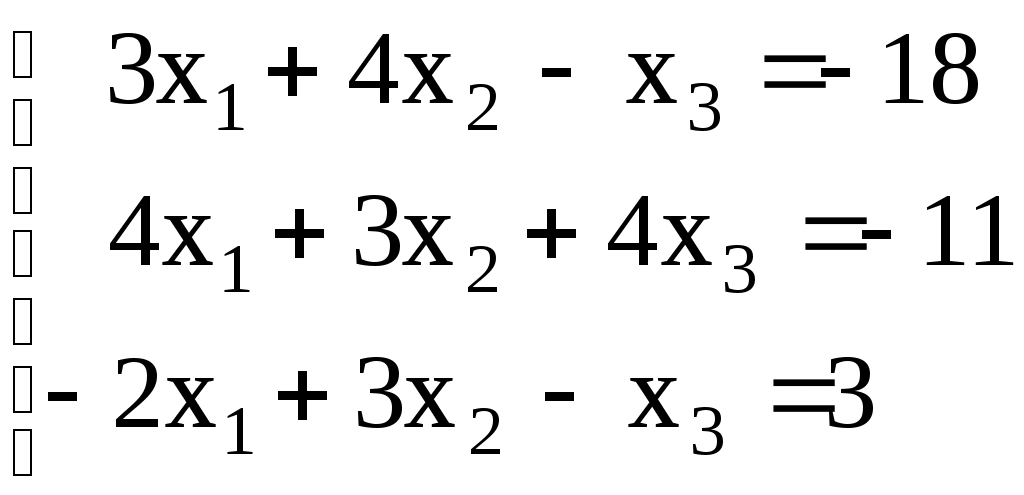 102. 102. 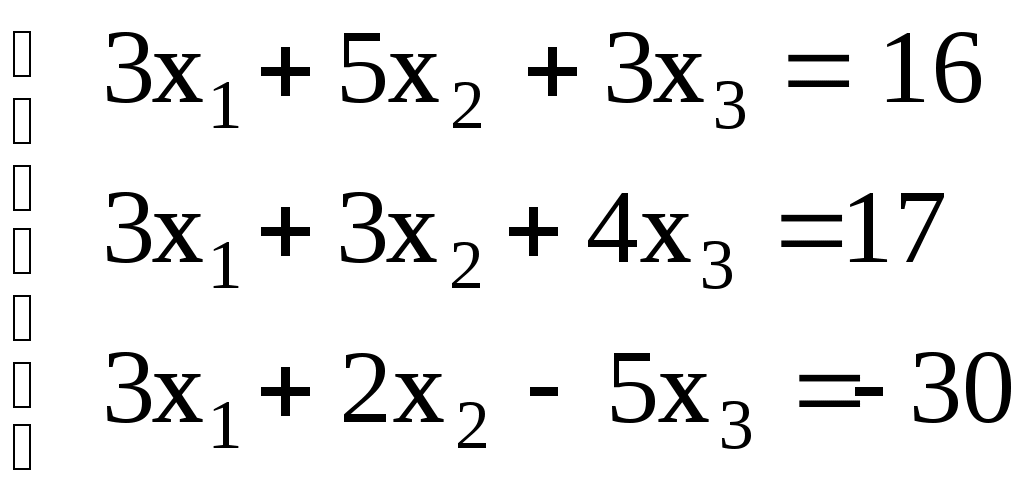 103. 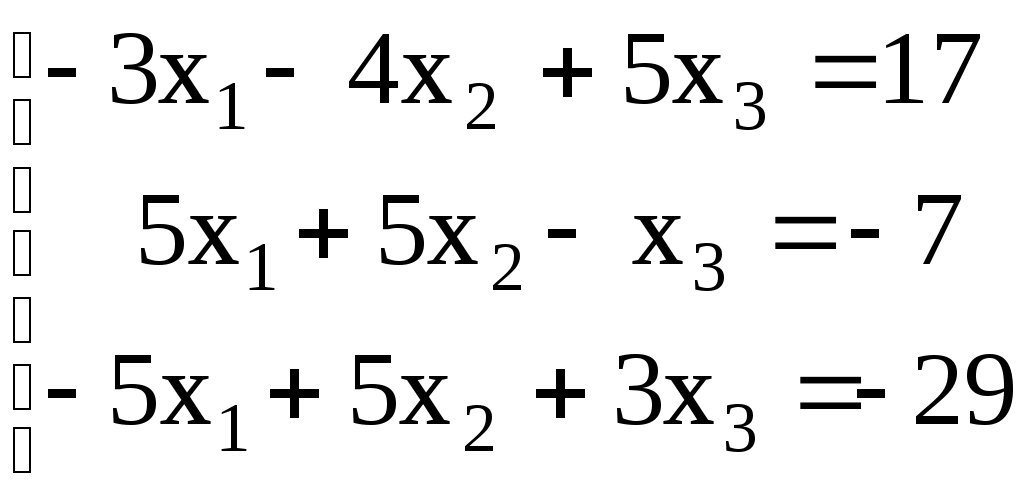 104. 104. 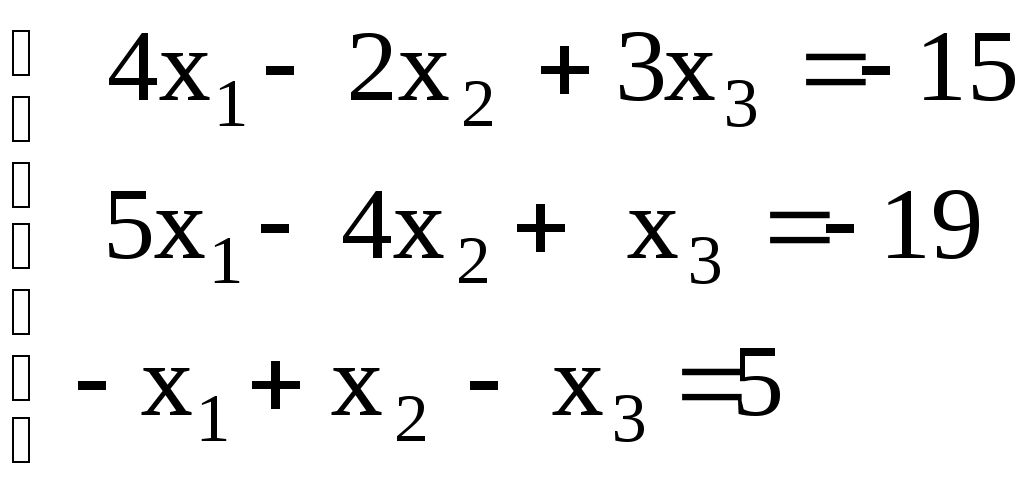 105. 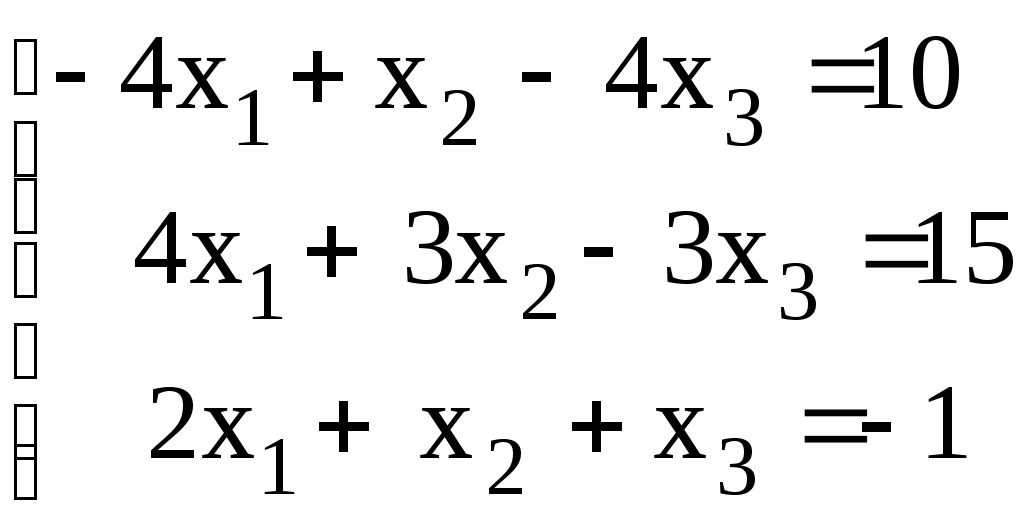 106. 106. 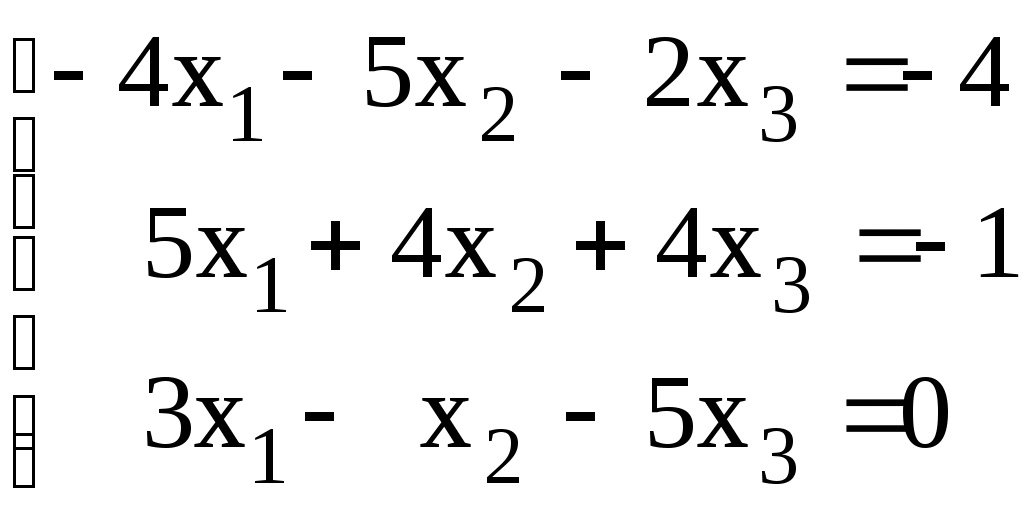 107. 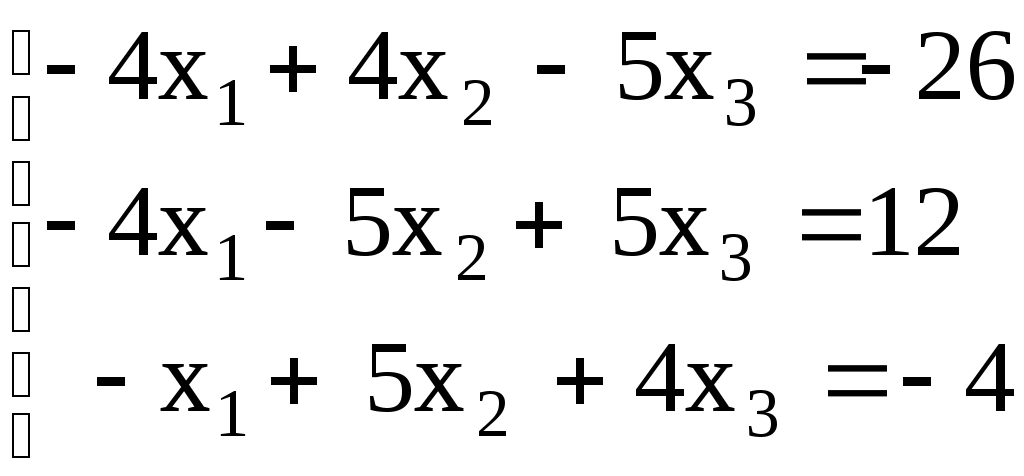 108. 108. 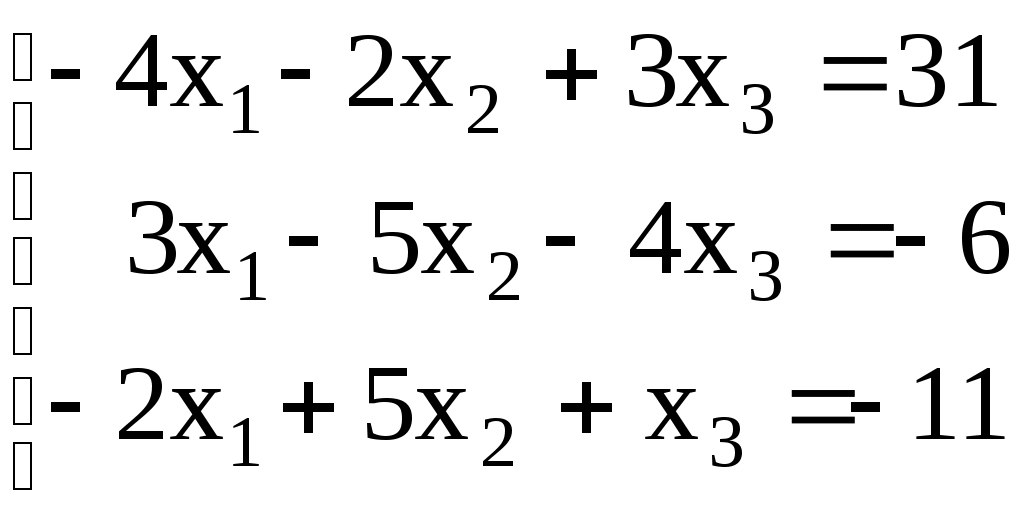 109. 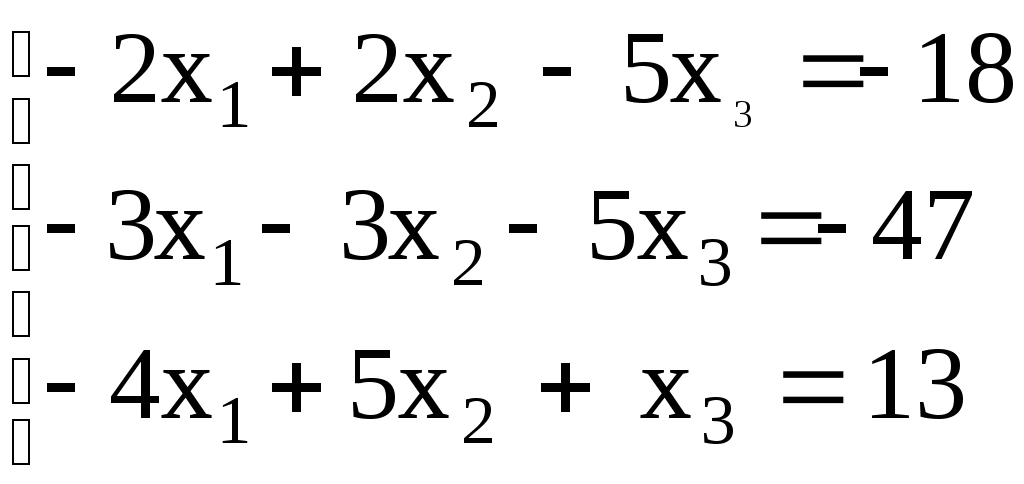 110. 110. 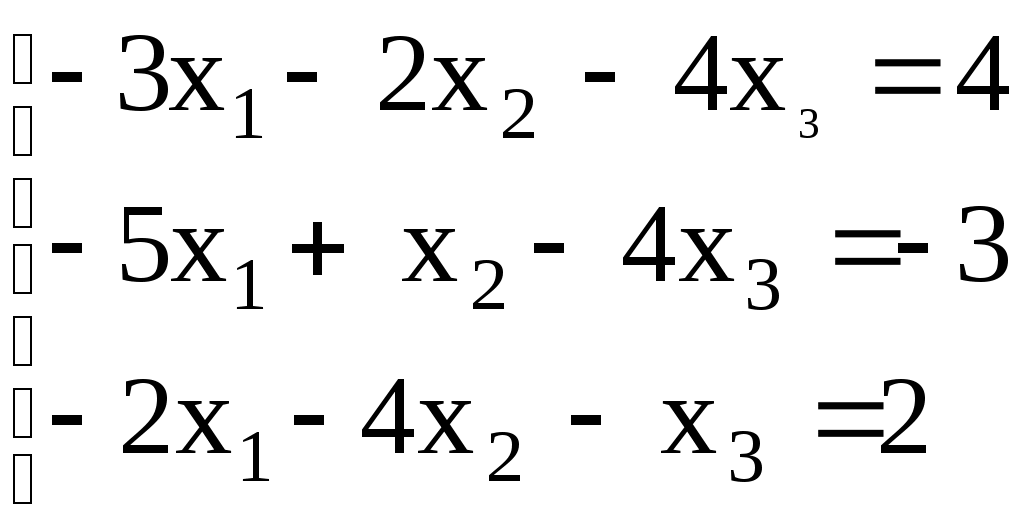 Методические указания к решению задач 101 – 110 Матрицы и определители Матрицей размера (m×n) называется прямоугольная таблица чисел, расположенных в m строках и n столбцах. Например, матрица 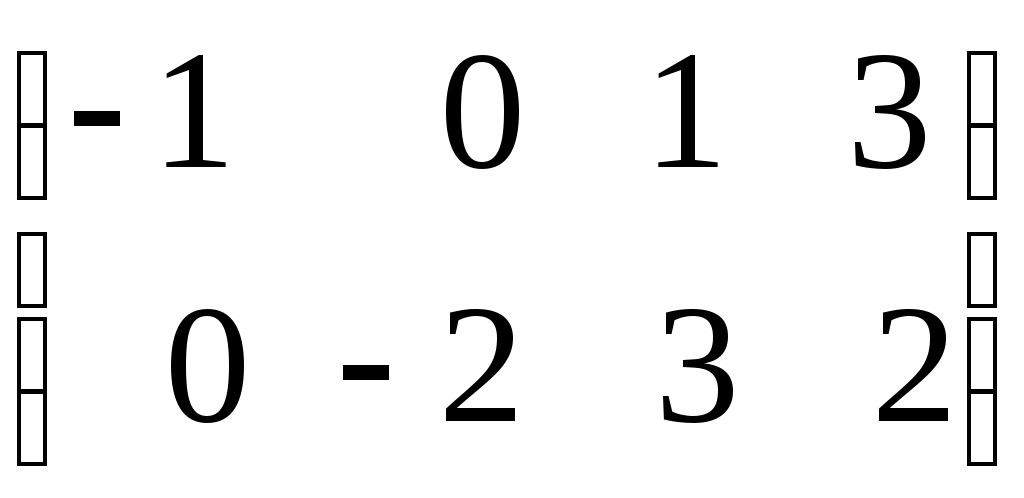 имеет размер имеет размер 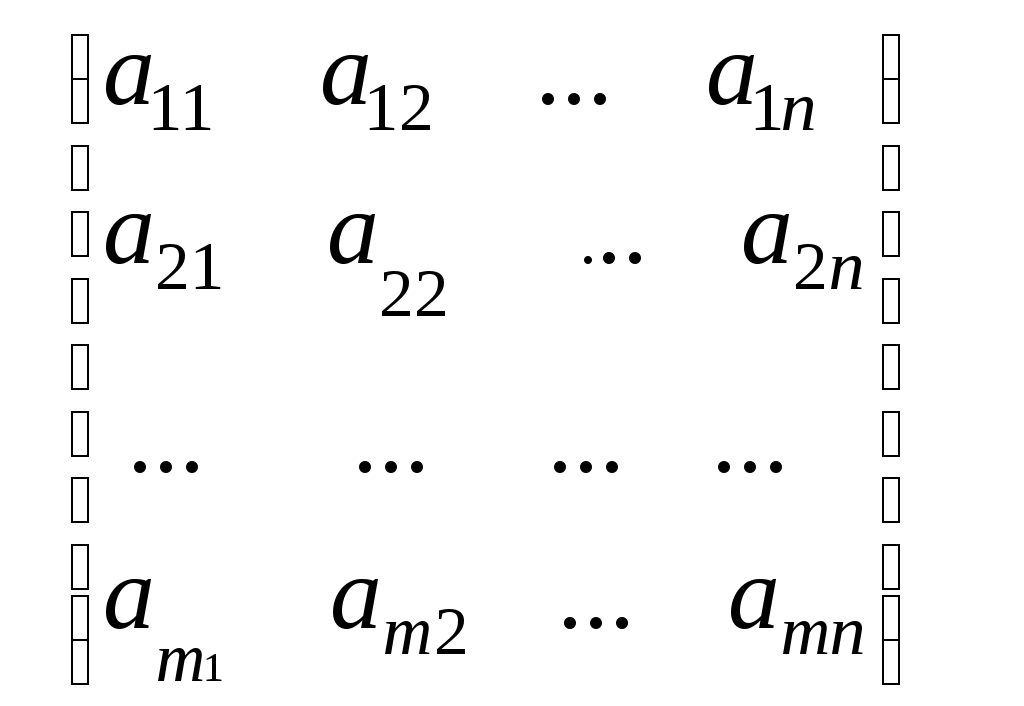 Числа аij(i=1,2,…,m), (j=1,2,…,n), входящие в состав данной матрицы, называются ее элементами. Индекс i указывает номер строки, в которой находится элемент, j – номер столбца. Матрица-строка – это матрица, состоящая из одной строки, матрица-столбец – матрица, состоящая из одного столбца. Матрица, в которой число строк равняется числу столбцов (m=n), называется квадратной, число ее строк (столбцов) называется порядком квадратной матрицы. Элементы Единичной матрицей Е называют квадратную матрицу, у которой элементы, стоящие на главной диагонали, равны единице, а все остальные элементы равны нулю. Например, единичная матрица третьего порядка запишется следующим образом: 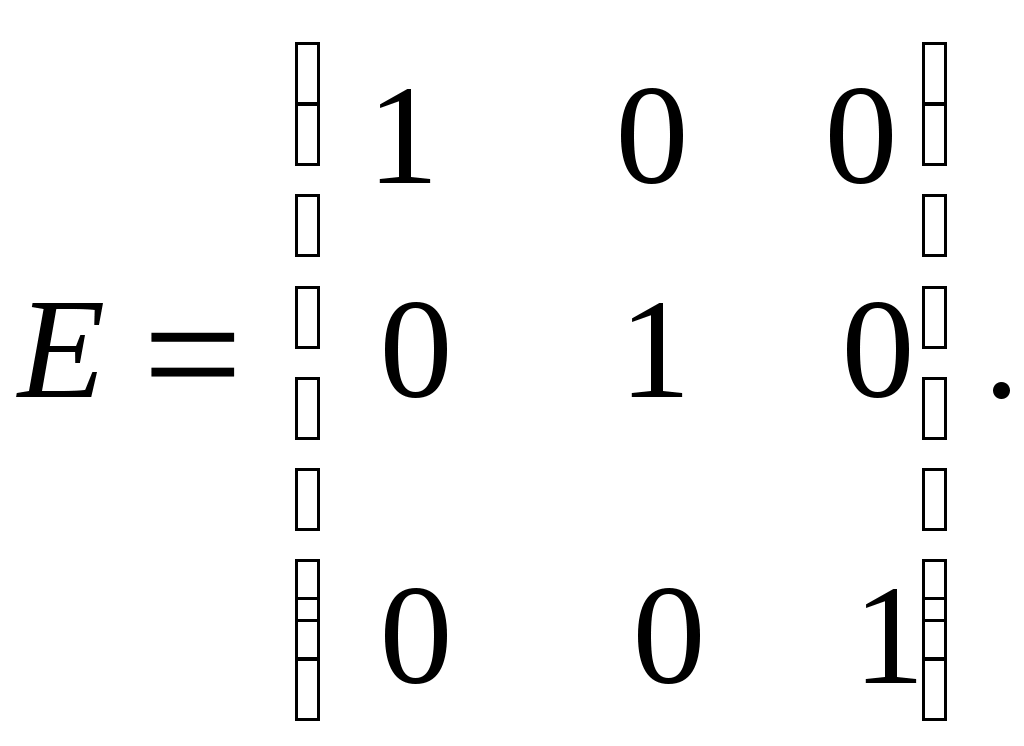 Для квадратных матриц вводится важнейшая числовая характеристика, которую называют определителем (детерминантом) и обозначают одним из символов: Δ, det A, Рассмотрим сначала квадратную матрицу второго порядка. Ее определителем 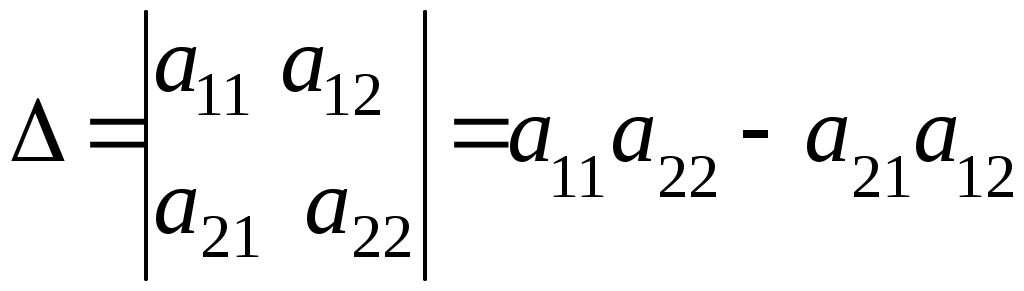 . .Пример 1: Рассмотрим теперь определитель третьего порядка. Δ = 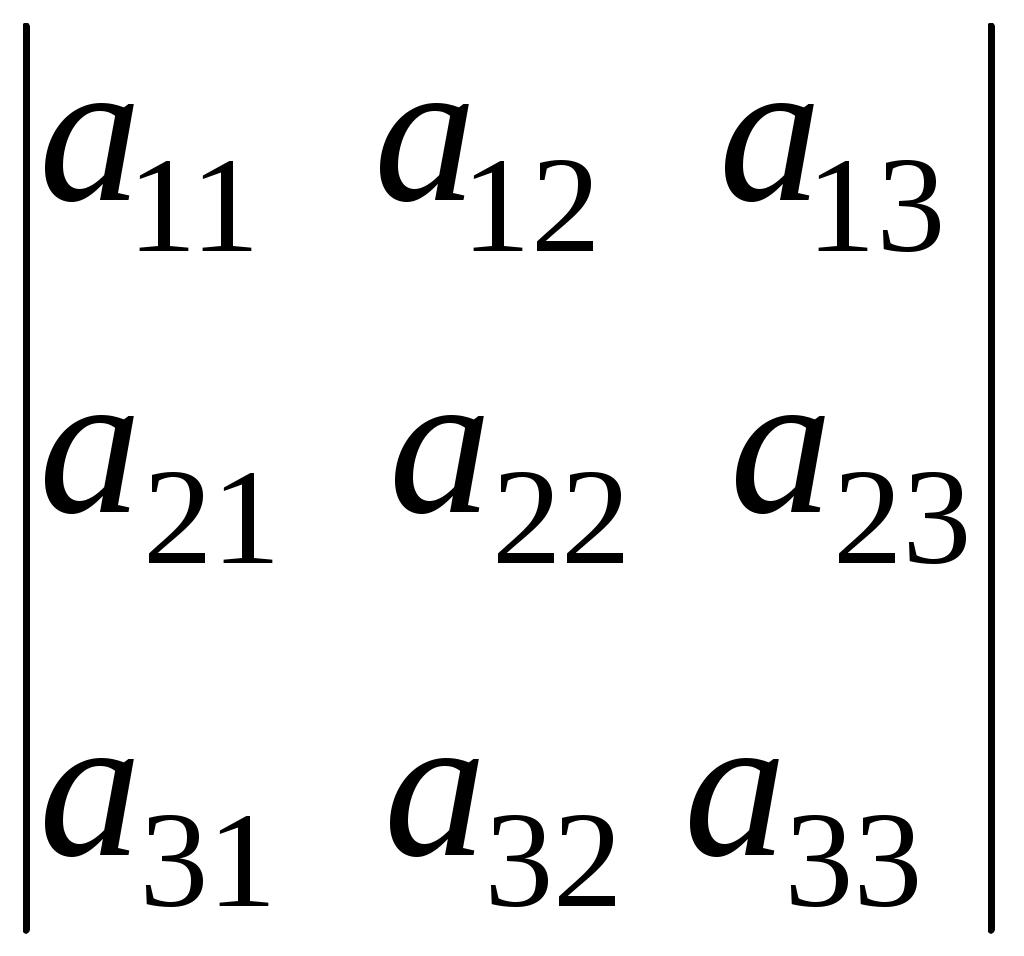 Вычисление этого определителя может быть сведено к вычислению определителей второго порядка. Для этого введем понятия минора и алгебраического дополнения. Минором Мij определителя третьего порядка называется определитель второго порядка, получающийся из данного определителя вычеркиванием i-ой строки и j-го столбца. Алгебраическим дополнением Аij элемента аij называется минор Мij , взятый со знаком +, если сумма (i +j) – четное число, и со знаком – , если сумма (i +j) есть нечетное число: 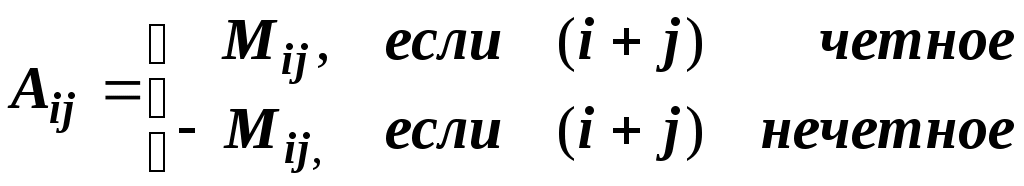 Определитель третьего порядка равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения: 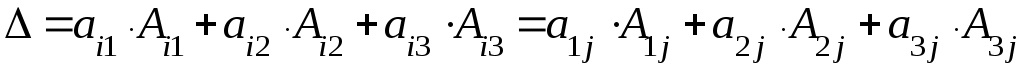 . .Пример 2:Вычислить определитель 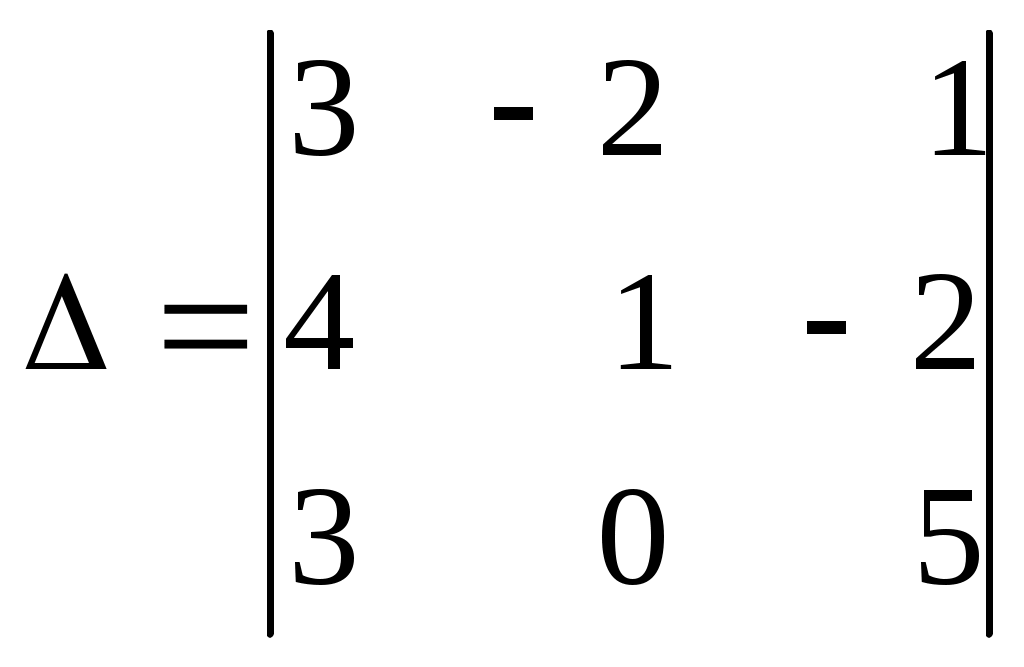 . .Решение: Найдем определитель Δ, используя элементы первой строки этого определителя и их алгебраические дополнения Вычислим А11 – алгебраическое дополнение элемента а11, то есть элемента, который находится в первой строке (i=1) и в первом столбце (j=1). Сумма i+j = 1+1 = 2 есть четное число, следовательно, А11 = М11. Далее, найдем М11. Для этого в определителе Δ вычеркнем первую строку, так как i=1, и первый столбец, так как j=1. Оставшиеся, невычеркнутые, элементы запишем в виде определителя второго порядка. Получим Найдем А12 – алгебраическое дополнение элемента а12. Здесь i=1, j=2. Сумма i+j = 1+2 = 3 есть нечетное число, значит А12 = – М12. Для нахождения М12 вычеркнем в определителе Δ первую строку и второй столбец. Из оставшихся чисел составим определитель второго порядка, таким образом, Аналогично, находим Следовательно, Квадратная матрица называется невырожденной, если ее определитель не равен нулю. Системой линейных алгебраических уравнений называется совокупность линейных уравнений 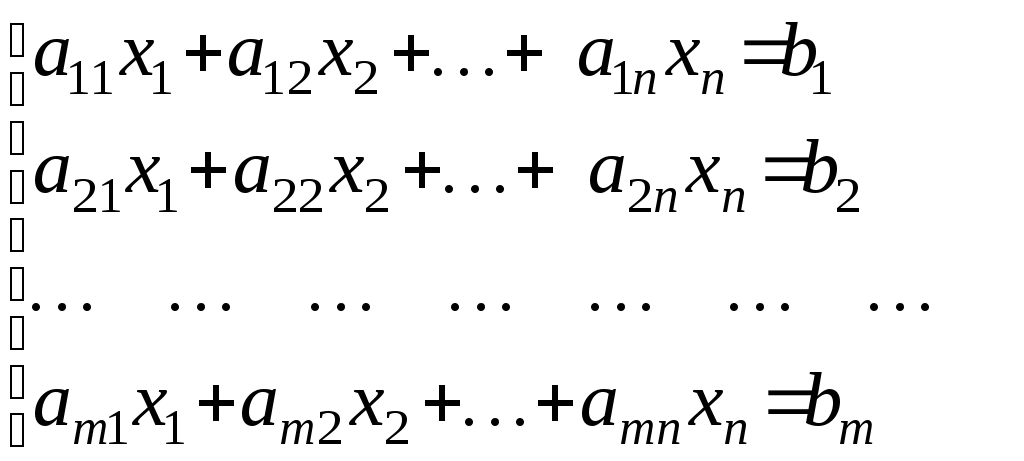 (1) (1)Здесь Решением системы (1) называется любая совокупность значений неизвестных Решить систему уравнений – это значит найти все ее решения. Система уравнений может иметь единственное решение, в этом случае она называется совместной определенной. Если система уравнений имеет бесконечное множество решений, тогда она называется совместной неопределенной. Система уравнений, не имеющая решений, называется несовместной. Матричный способ решения системы Рассмотрим матричный способ решения системы на конкретном примере. Задача. Показать, что система линейных уравнений имеет единственное решение. Найти его матричным способом. Сделать проверку. 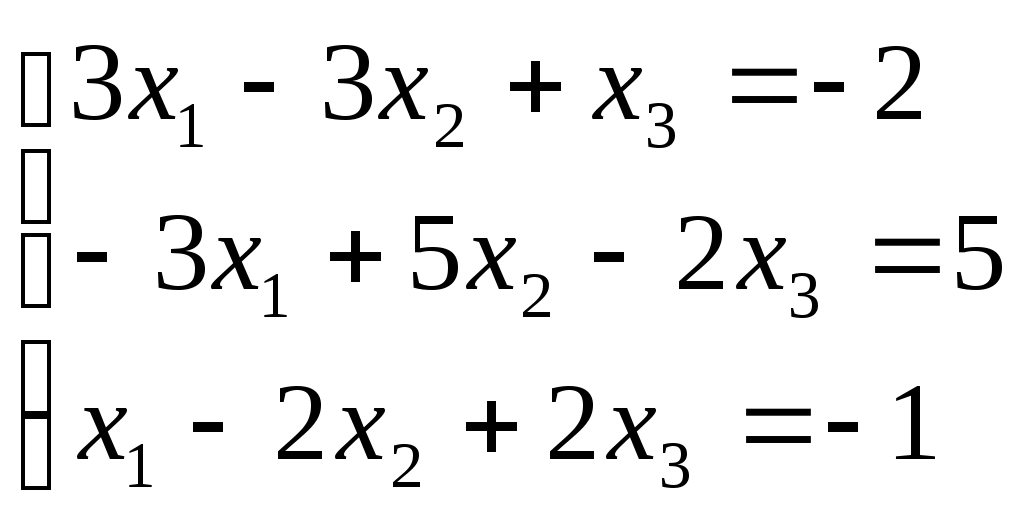 (2) (2)Решение: Свяжем с этой системой матрицы A, X, B. 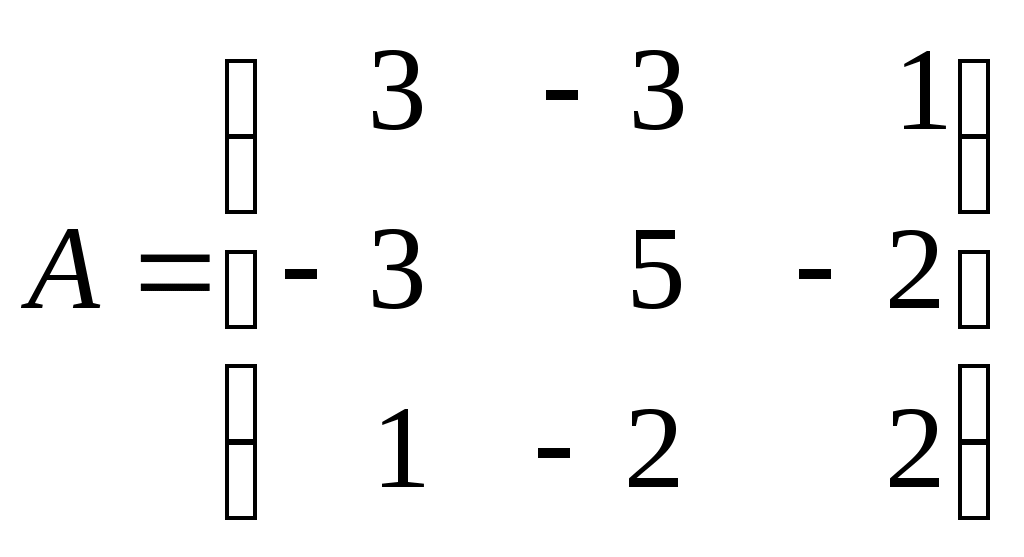 , , 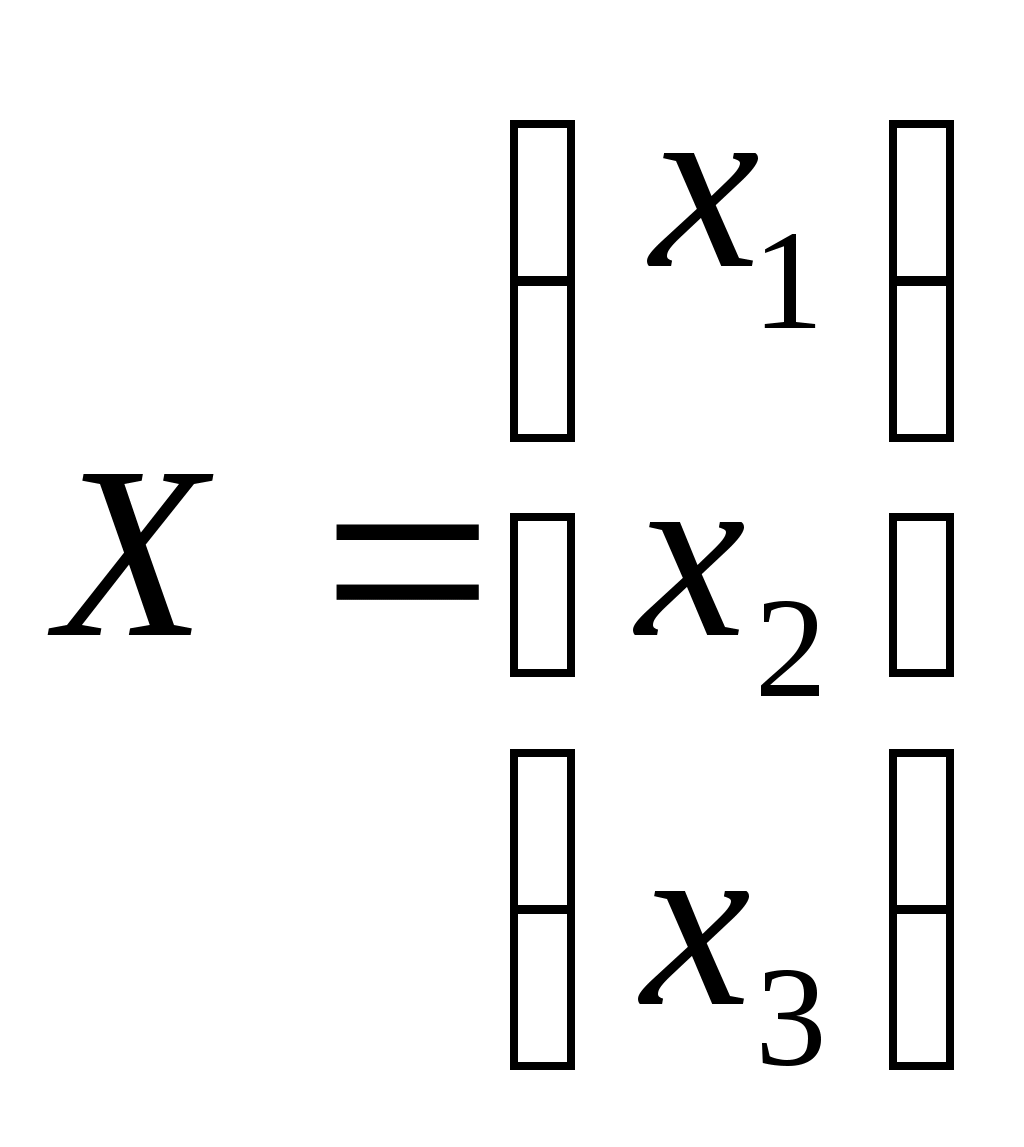 , , 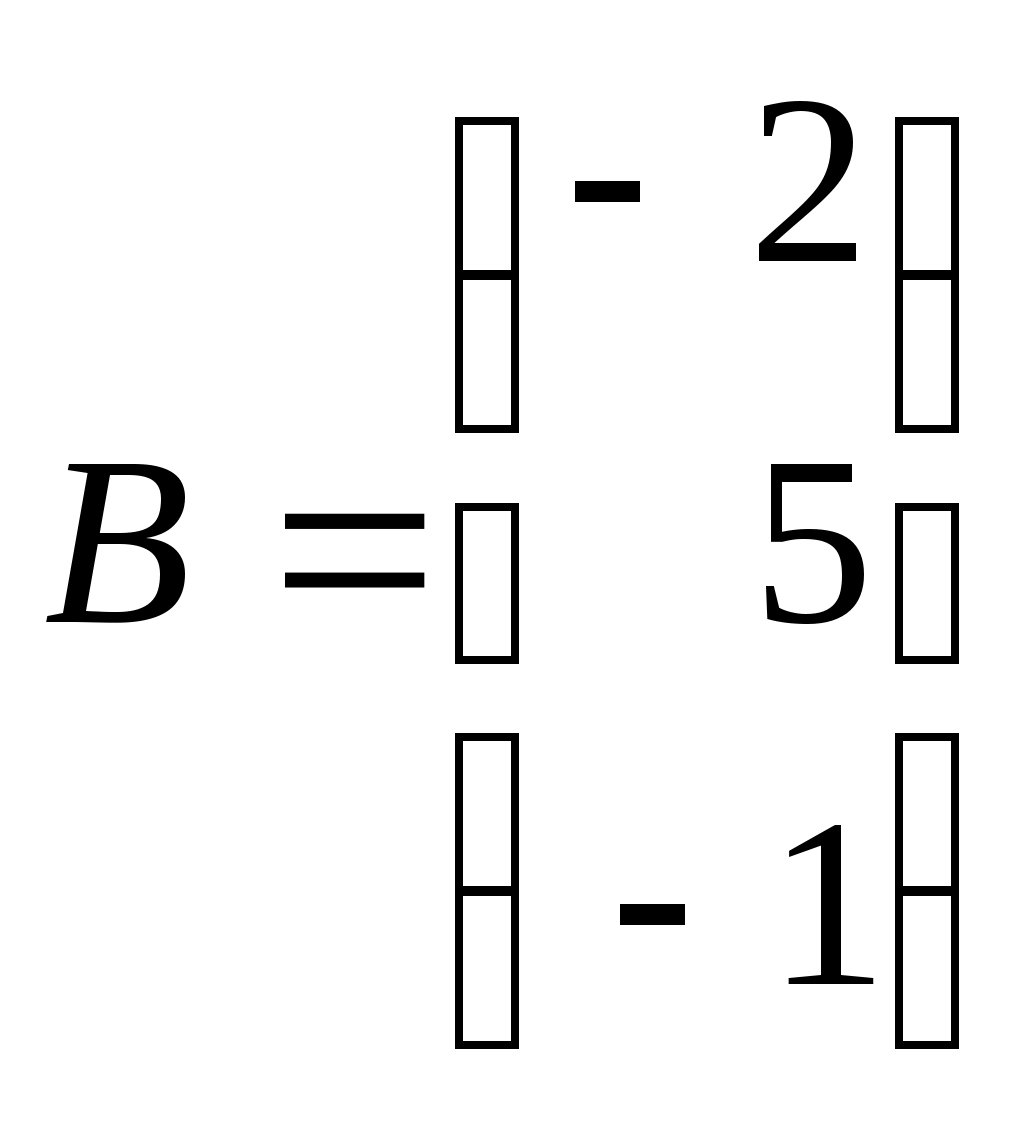 Матрица А – это матрица, составленная из коэффициентов при неизвестных. Матрица Х есть матрица-столбец из неизвестных. Матрица В – матрица-столбец, составленная из свободных членов. Систему уравнений (2) можно записать с помощью этих матриц: 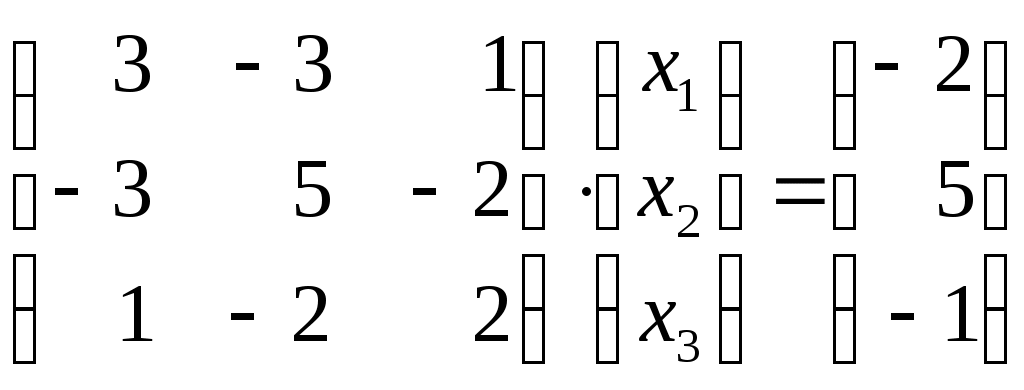 или кратко, в матричном виде, А∙Х = В Поясним, как матрицу А умножить на матрицу-столбец Х. Заметим вначале, что результат произведения А∙Х есть матрица-столбец из трех элементов. Для того, чтобы получить первый элемент (в первой строке) этой матрицы, возьмем первую строку матрицы А - это числа 3; -3; 1, и умножим их соответственно на элементы столбца х1, х2, х3 матрицы неизвестных Х, затем полученные произведения сложим: 3∙х1+(-3)∙х2+1∙х3. Аналогично, поступим со второй и третьей строками матрицы А. Таким образом, 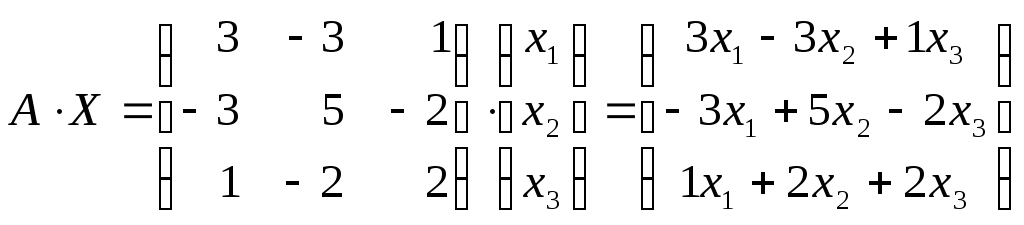 Заметим, что мы получили матрицу, элементы которой есть ни что иное, как левые части уравнений нашей системы (2). Две матрицы называются равными, если у них соответствующие (стоящие на одинаковых местах) элементы равны. В нашем случае матрица А∙Х равна матрице В: 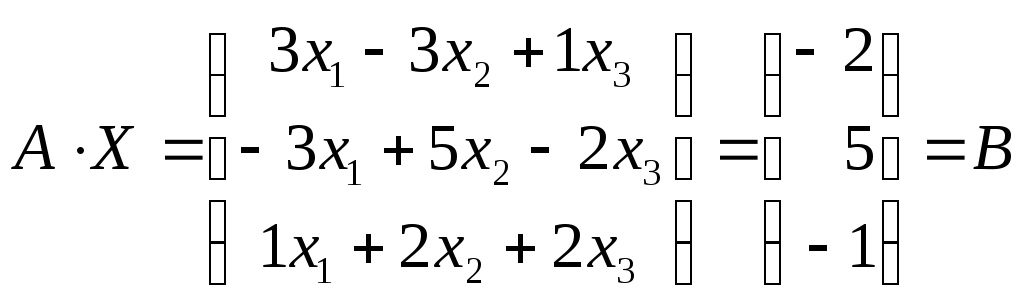 Действительно, равенства соответствующих элементов этих матриц есть уравнения нашей системы. Таким образом мы показали, что систему (2) можно записать в виде А∙Х = В. Решение системы (2) также можно записать с помощью матриц. Для этого введем понятие обратной матрицы. Матрица А-1 называется обратной для квадратной невырожденной матрицы А, если А-1∙А= А∙А-1 = Е, где Е единичная матрица такого же порядка, что и матрица А. Отметим, что умножение матриц А и А-1 происходит по тому же принципу, что и описанный выше, а именно: матрицу А умножим на первый столбец матрицы А-1 получим первый столбец матрицы произведения А∙А-1, затем матрицу А умножим на второй столбец матрицы А-1, получим второй столбец матрицы произведения, аналогично получим третий столбец. Далее, если матрица А невырожденная ( Х=А-1∙ В, где обратную матрицу А-1 можно записать, используя алгебраические дополнения:  Следует обратить внимание на то, что алгебраические дополнения, соответствующие элементам строк данной матрицы А, располагаются в столбцах с теми же номерами, что и строки. Покажем, что наша система имеет единственное решение, и найдем его. Сначала найдем все алгебраические дополнения (более подробные разъяснения см. в примере 2). Найдем определитель матрицы А. 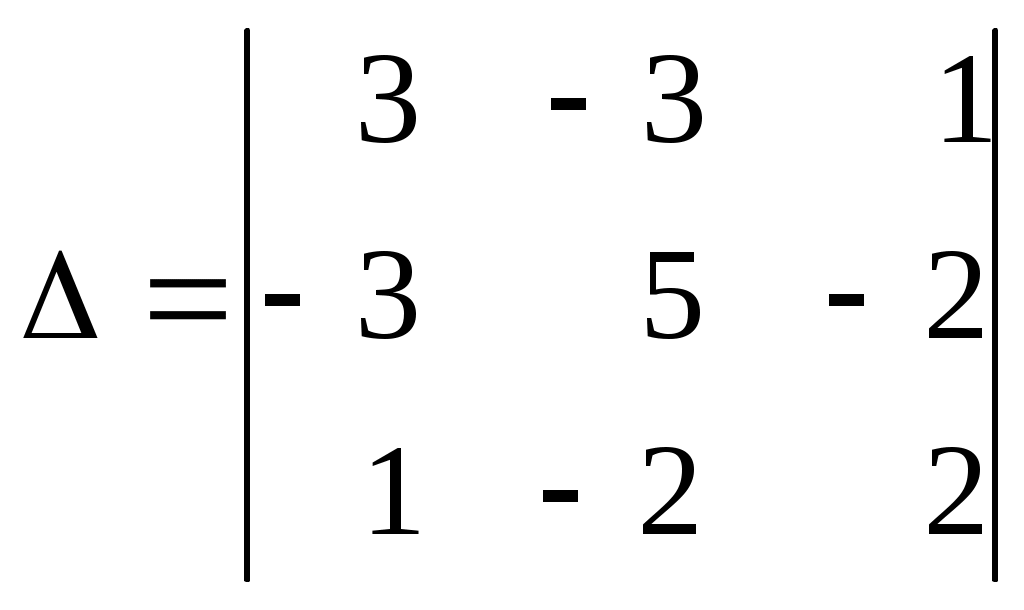 Для вычисления определителя используем его разложение по элементам первой строки: Тогда Δ = 3∙6 + (-3)∙4 + 1∙1 = 18 - 12 + 1 = 7. Видим, что Δ=7≠0. Значит, наша система имеет единственное решение. Составим А-1: 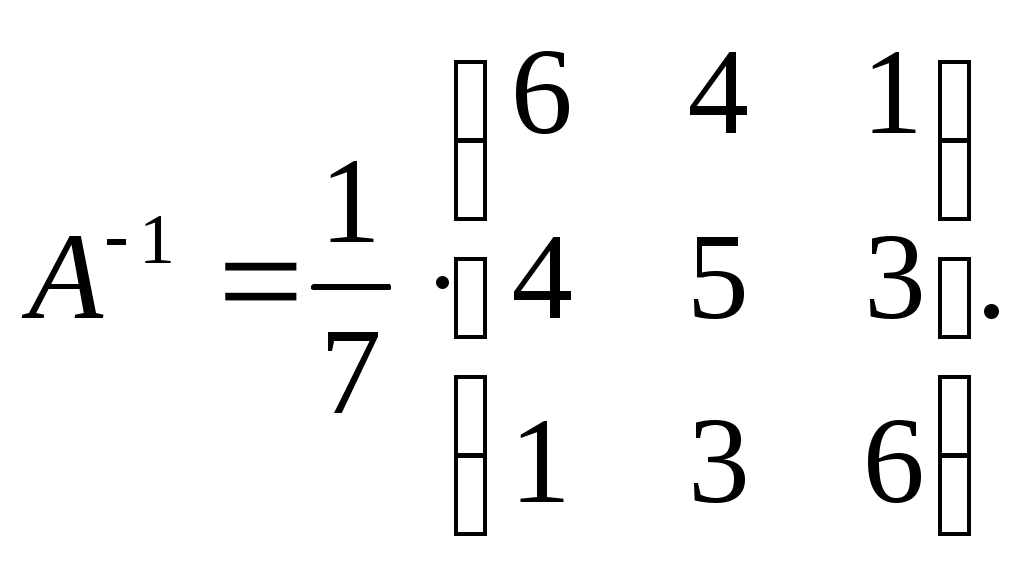 Найдем решение данной системы уравнений: 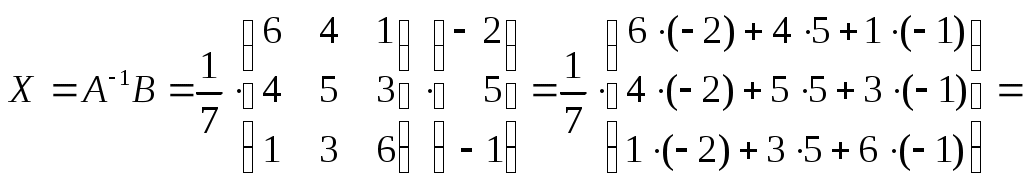 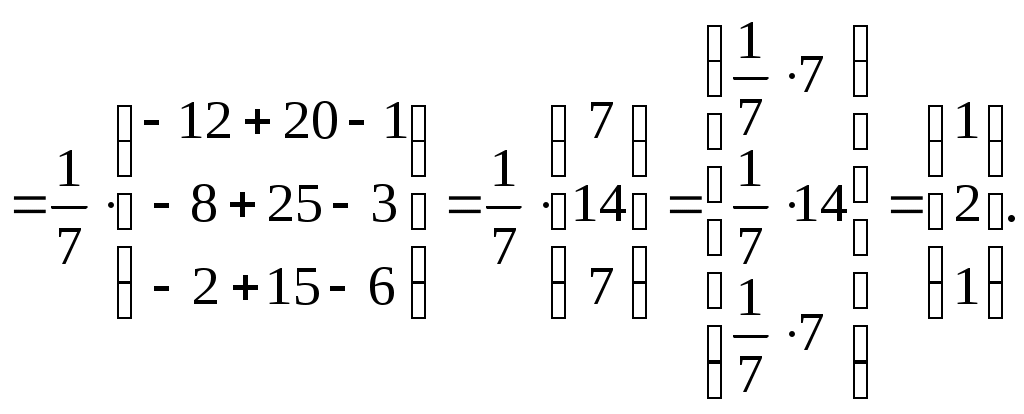 Здесь, в последнем действии, мы воспользовались правилом умножения матрицы на число: нужно каждый элемент матрицы умножить на это число (в примере это число Далее, из равенства матриц 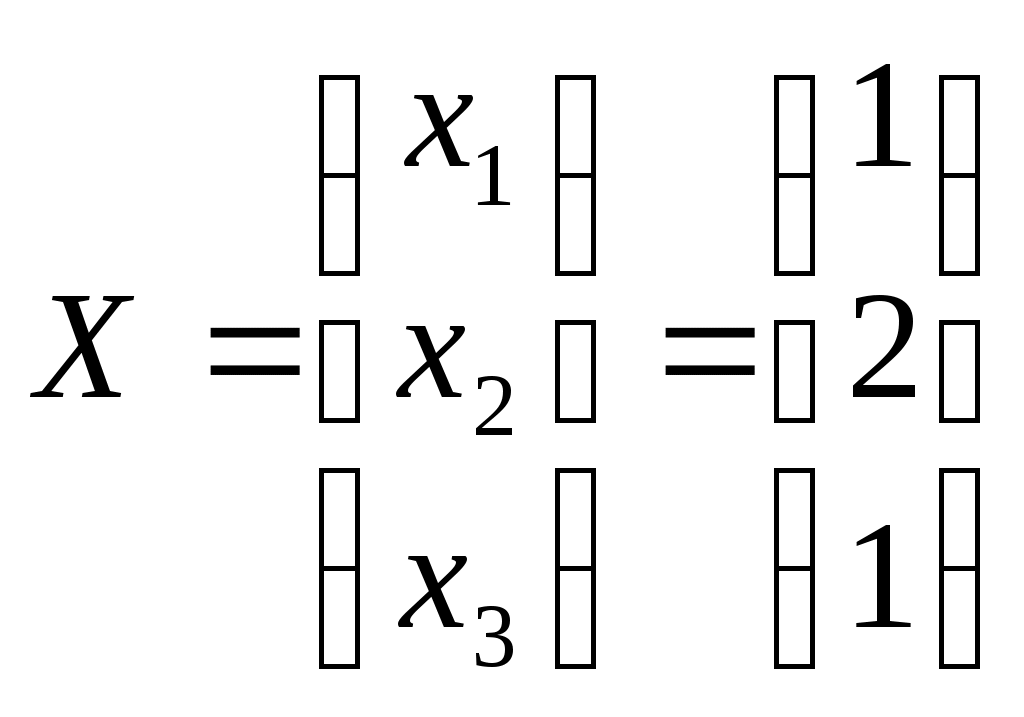 , ,Проверка: имеем х1 = 1, х2 = 2, х3 = 1. Подставим найденные значения неизвестных х1, х2, х3 в каждое уравнение системы 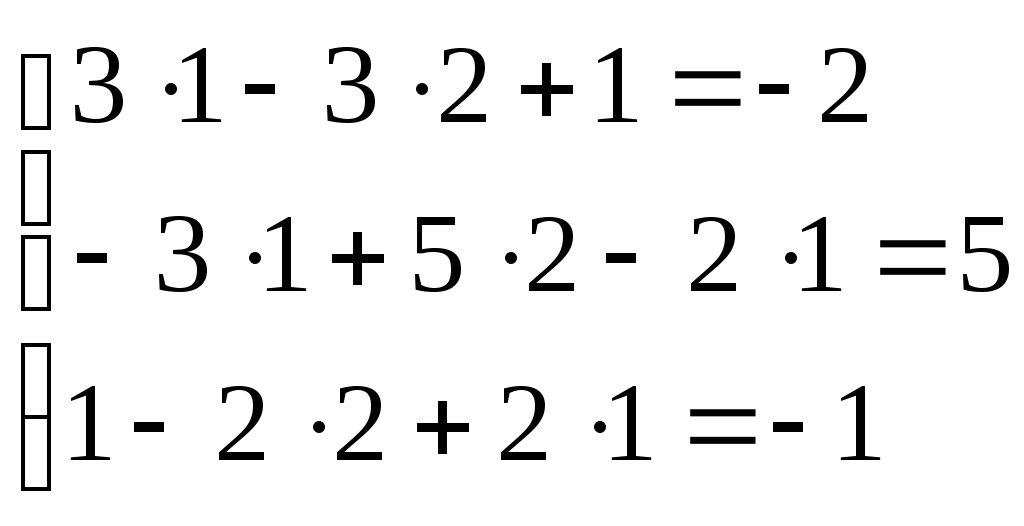 Все равенства верные. Ответ: (1; 2; 1) – единственное решение системы. |
