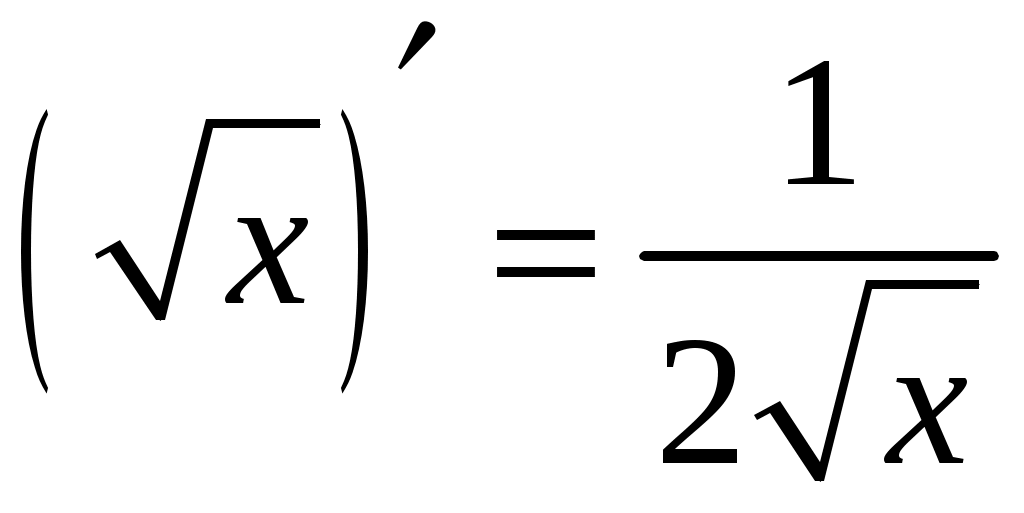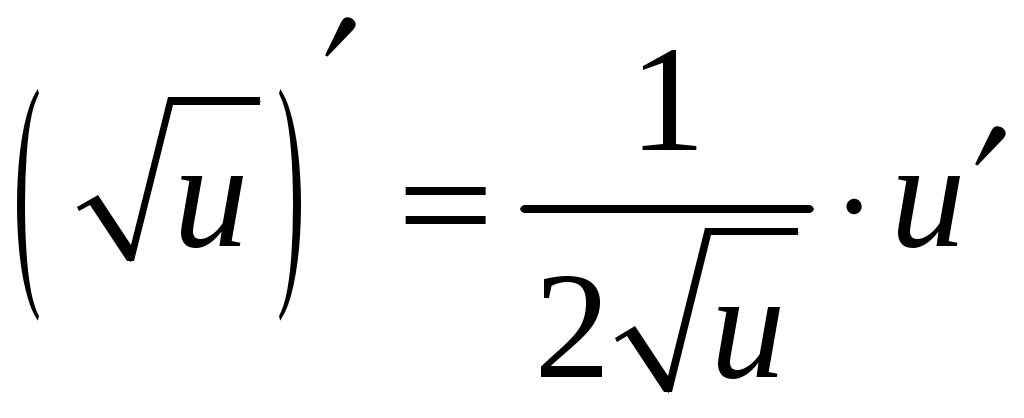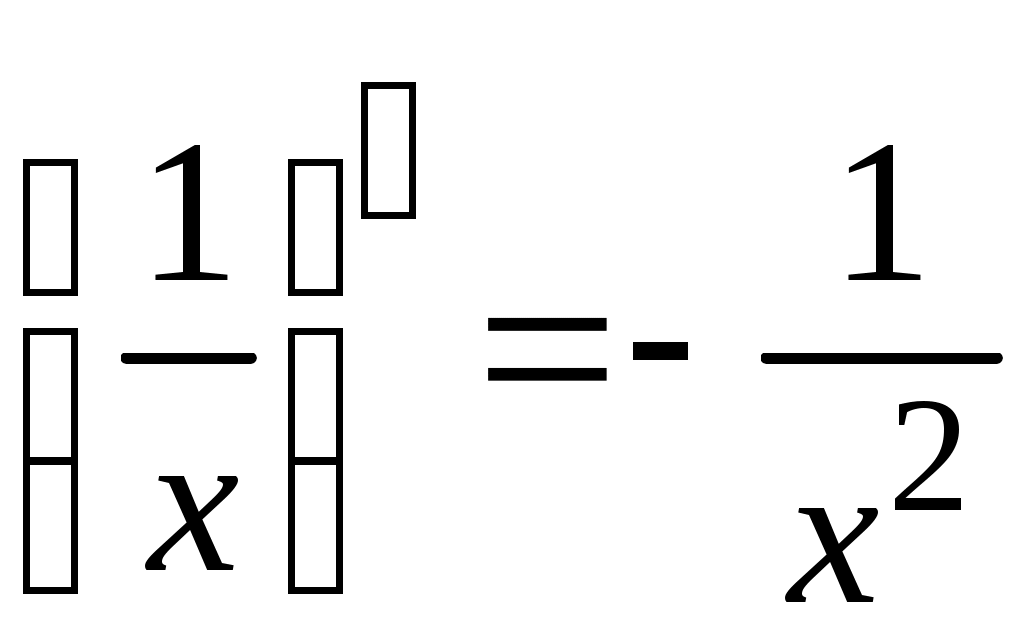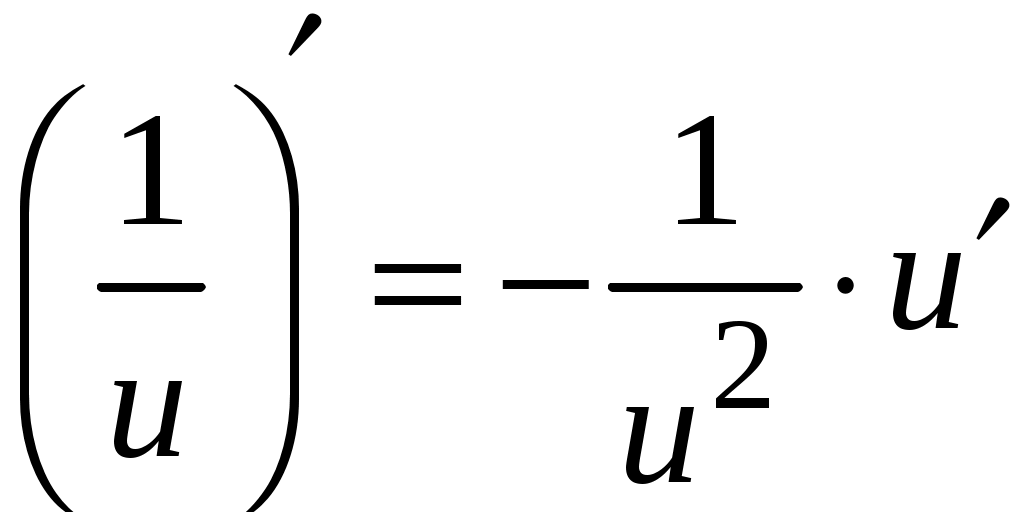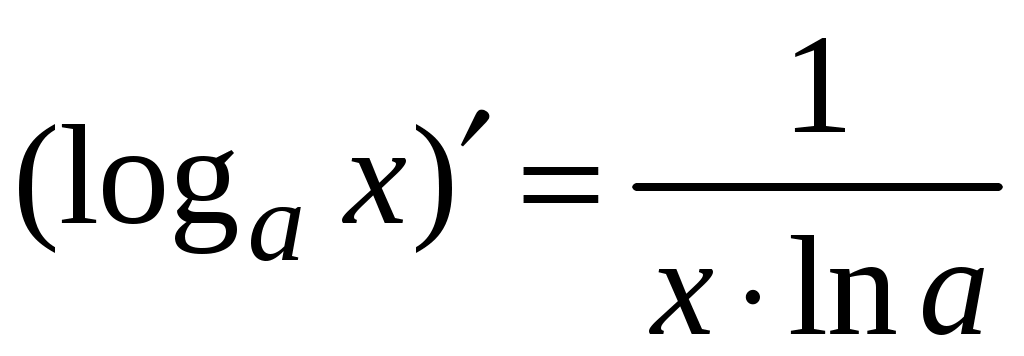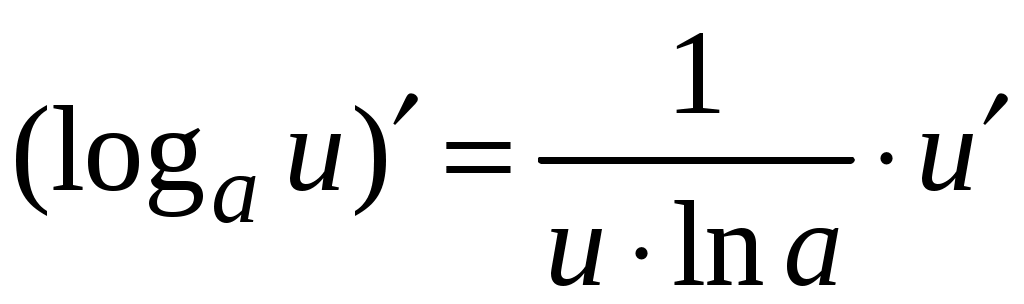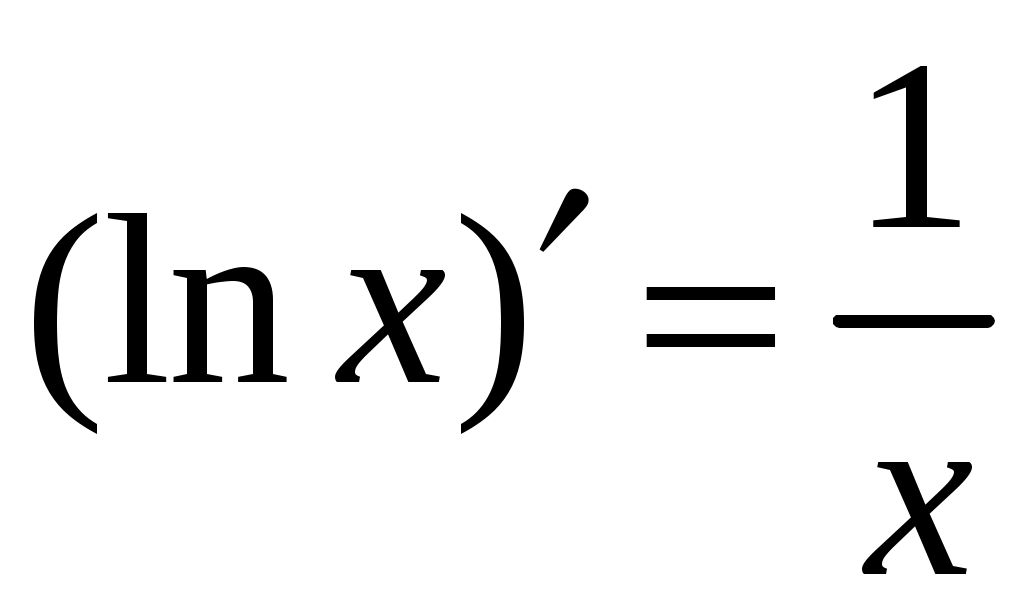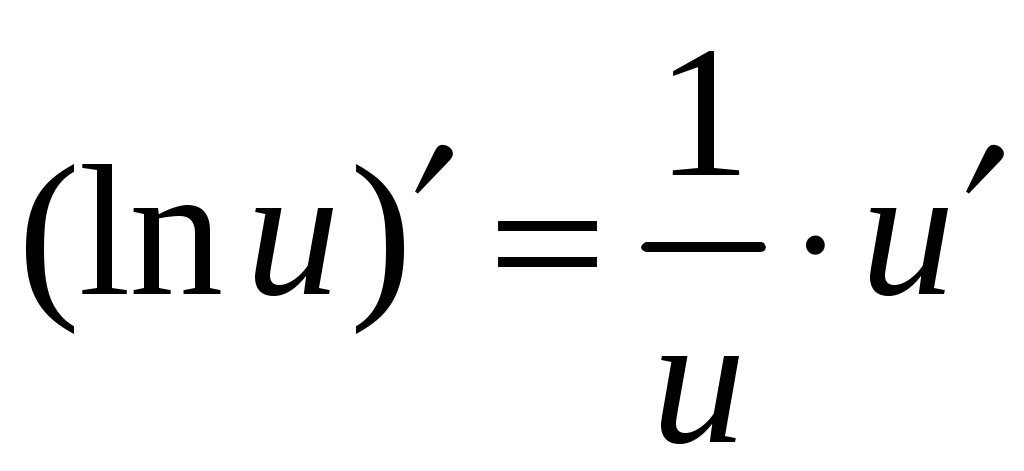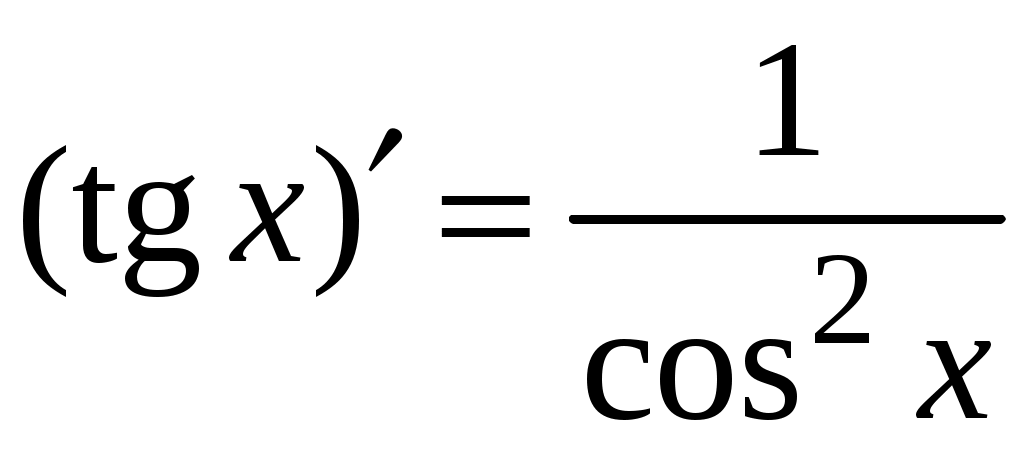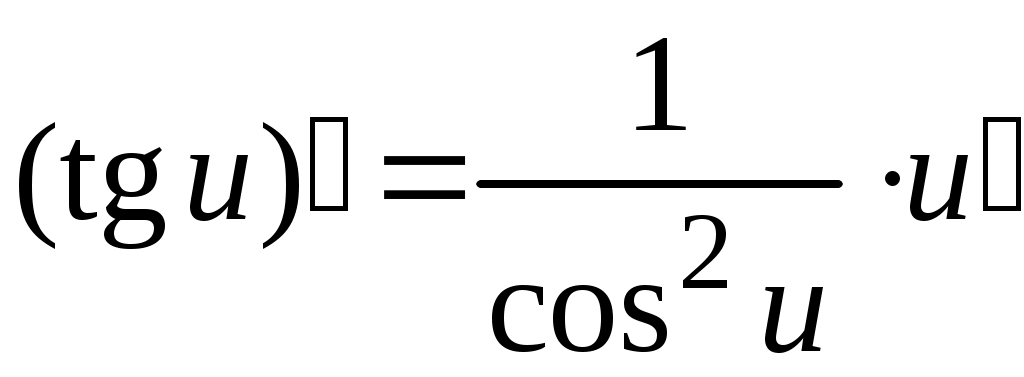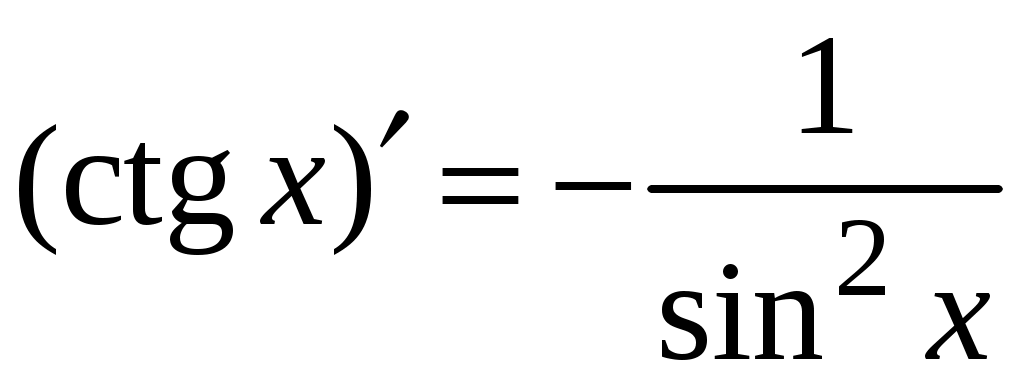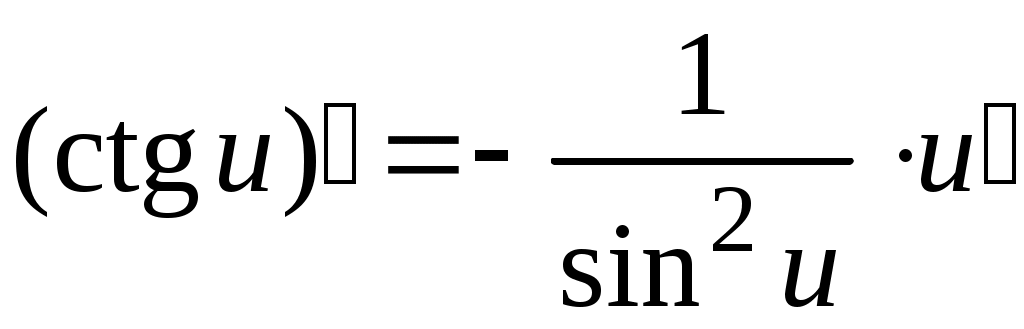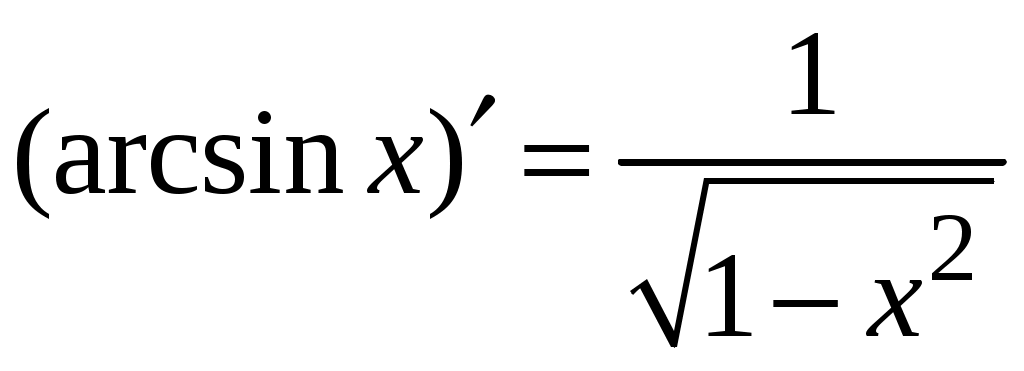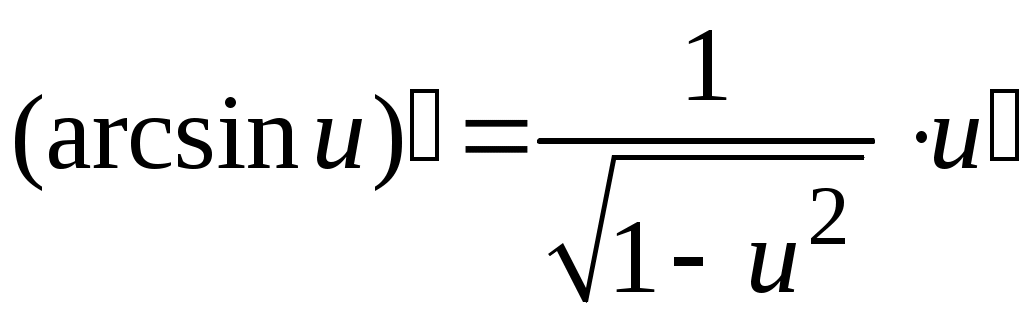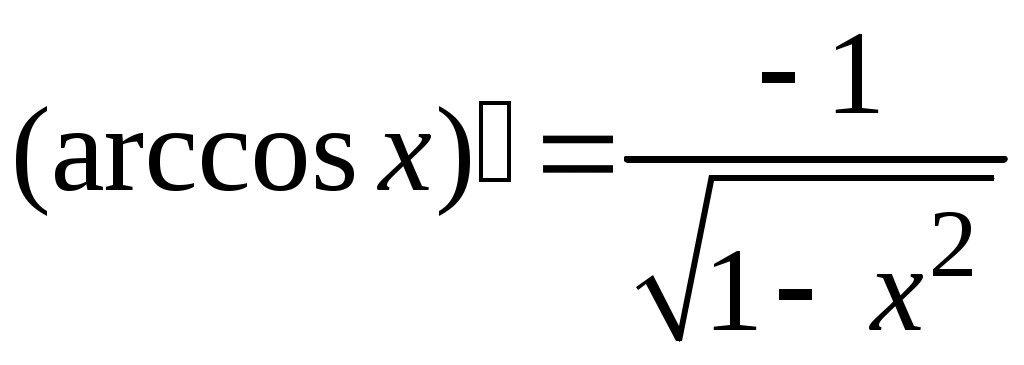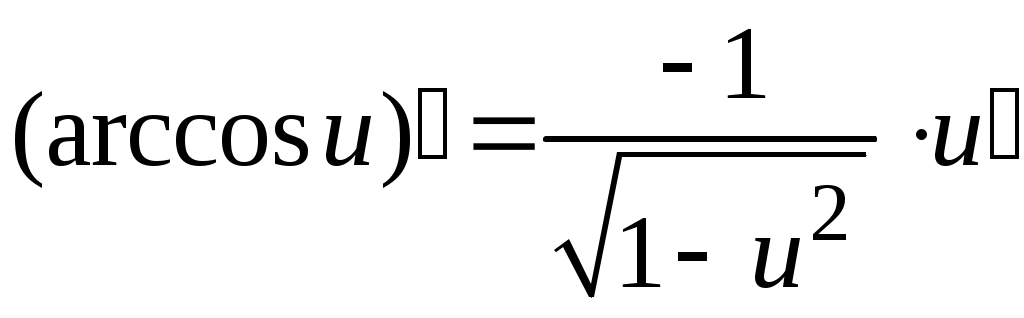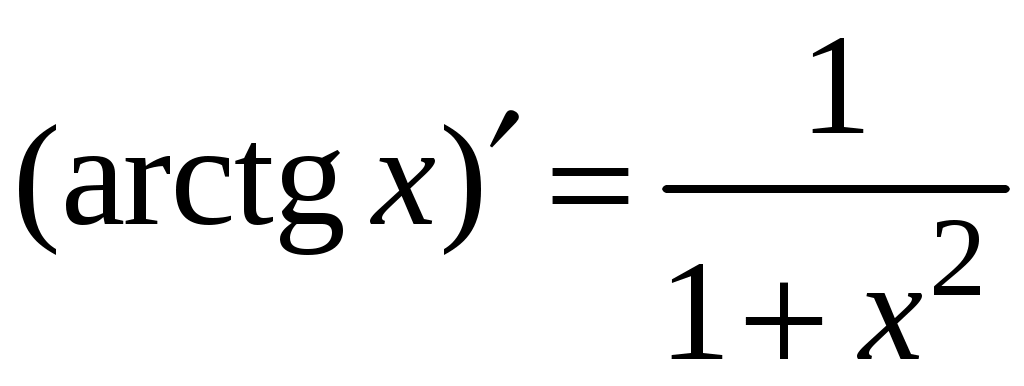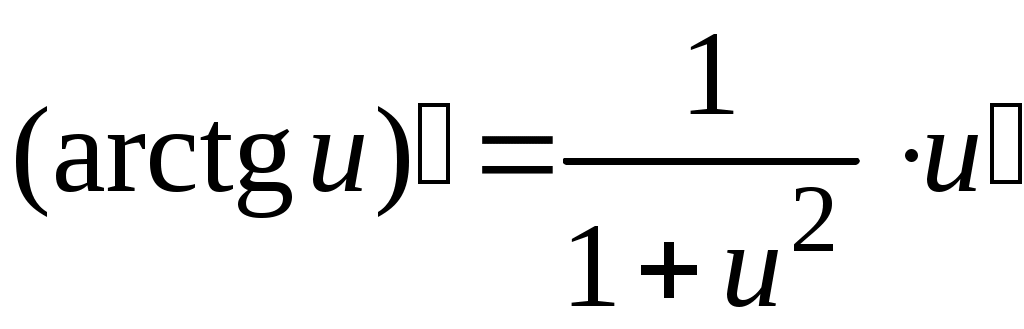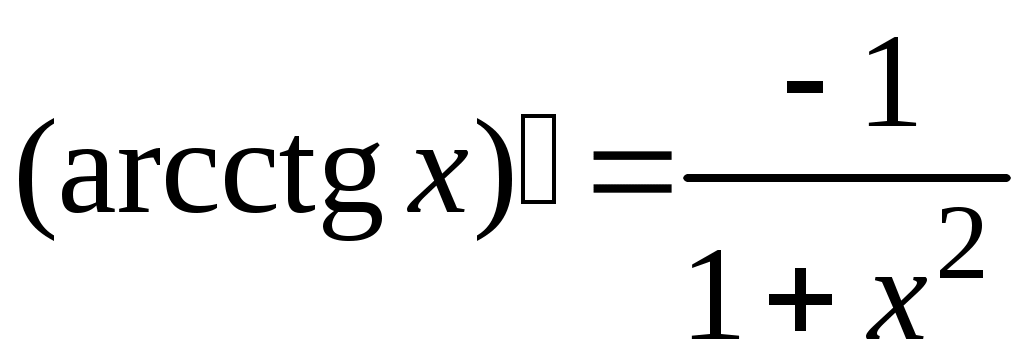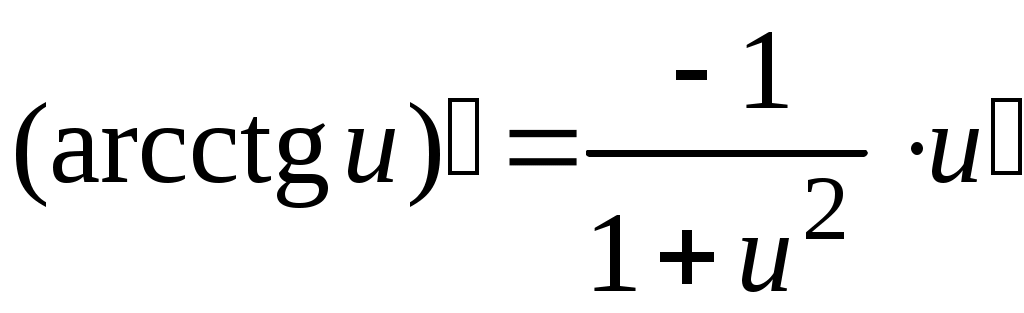Математика. Б1.Б.11_ММ Математика 38.03.02. Методические указания и задания к занятиям семинарского типа, контрольной и самостоятельной работе по дисциплине математика
 Скачать 2.28 Mb. Скачать 2.28 Mb.
|
5. Таблица производных.
Задача. Найти производные данных функций и их дифференциалы. Решение. а) 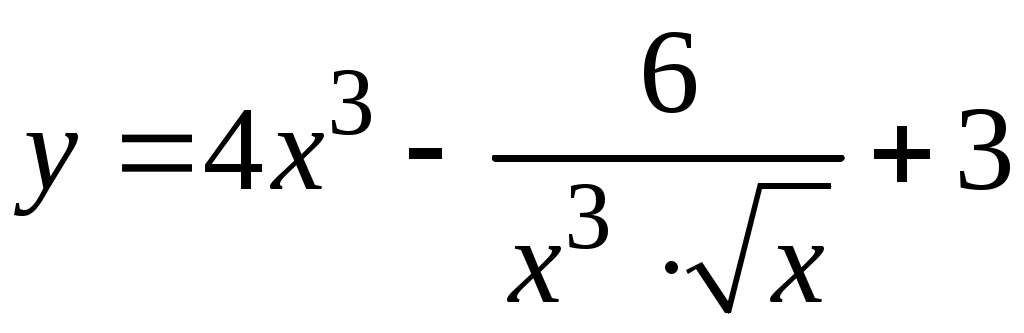 . .Приведем функцию y к виду, удобному для дифференцирования, используя правила действия со степенями 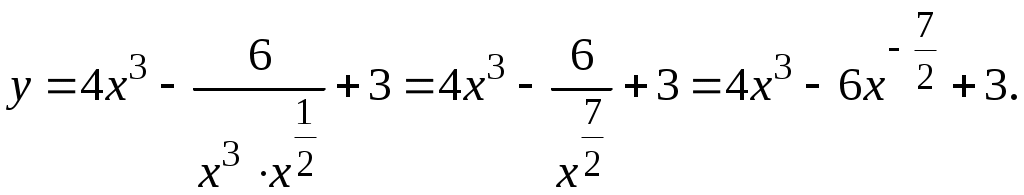 По правилу дифференцирования суммы и разности функций: 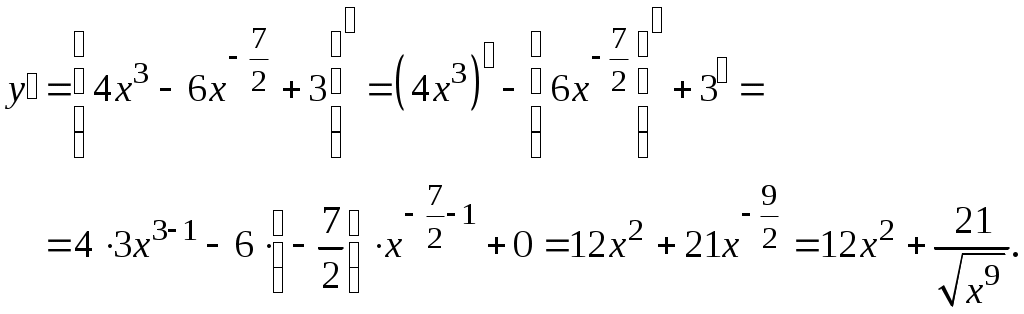 Тогда дифференциал функции y: 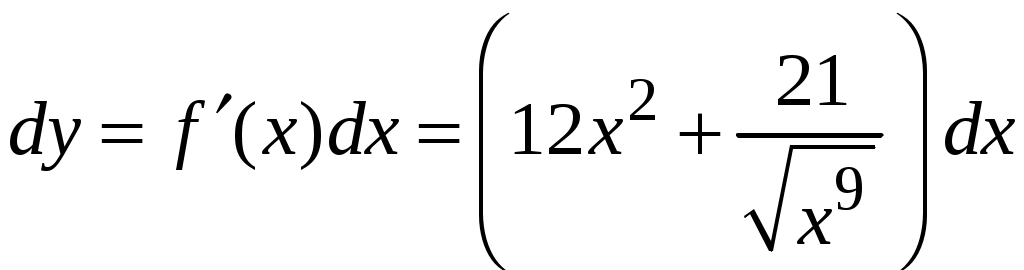 . .б) 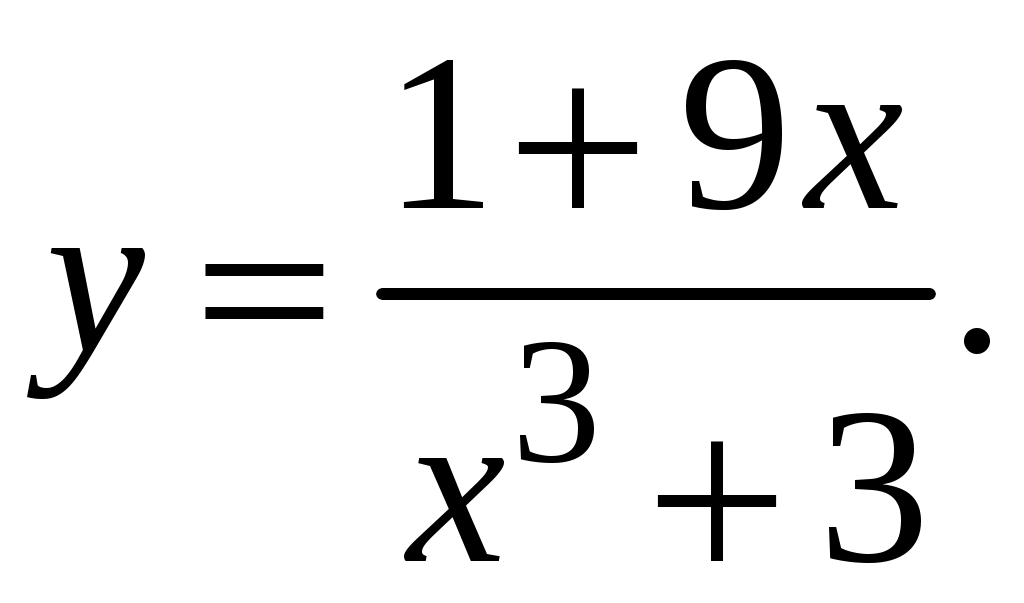 Воспользуемся правилом дифференцирования частного 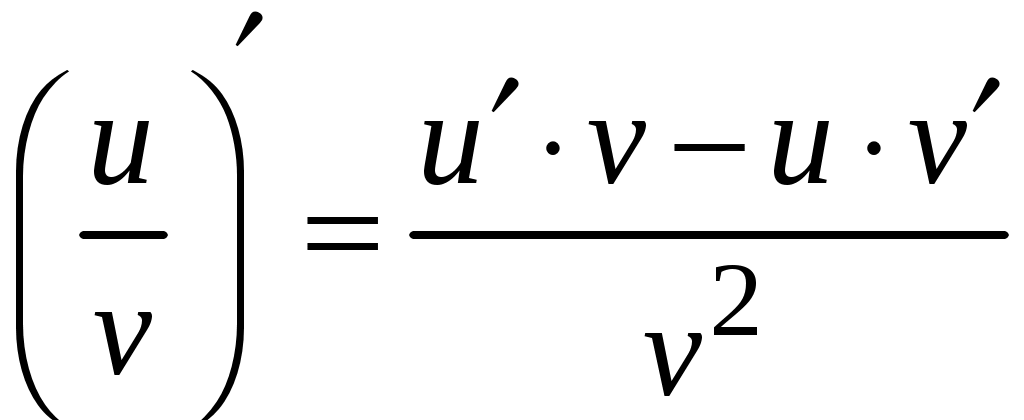 , где , где 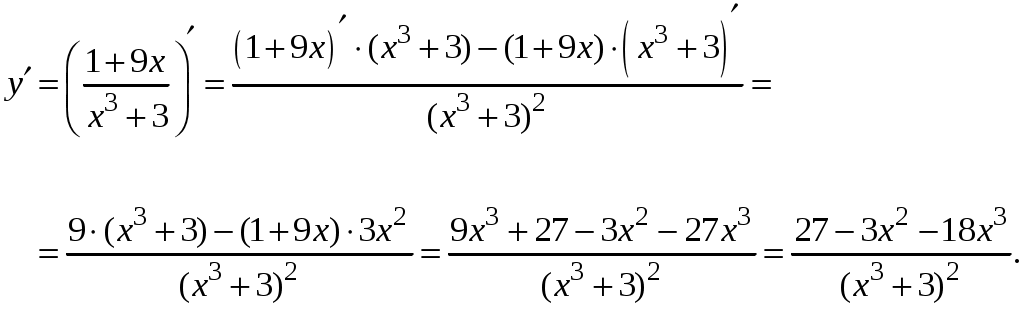 Тогда дифференциал функции y: 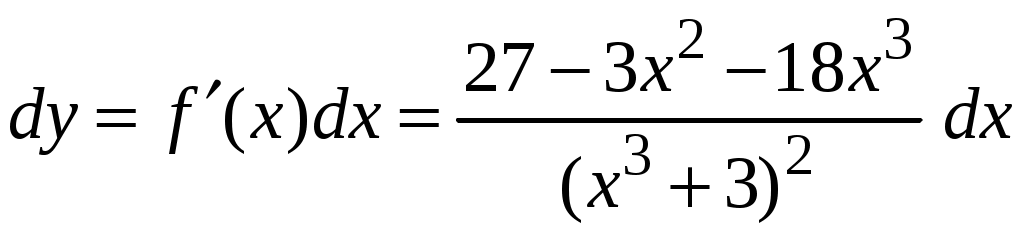 . .в) Функция 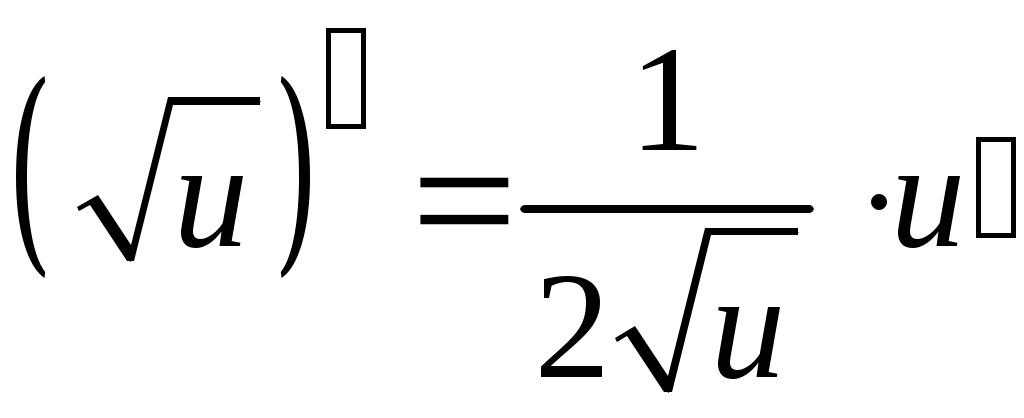 . .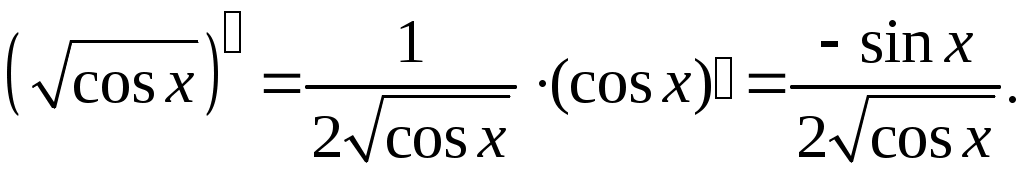 Производную функции 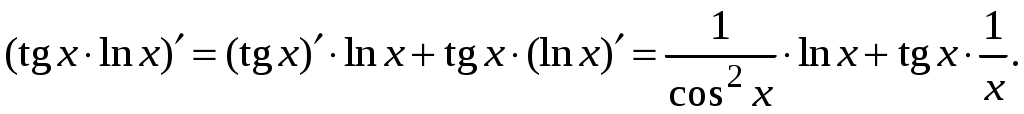 Таким образом, 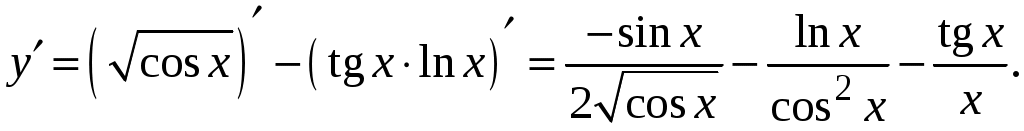 Тогда дифференциал функции y: 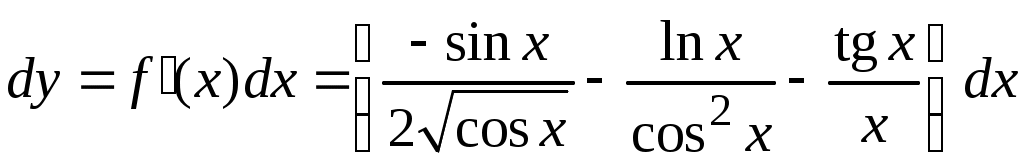 . .Исследование функции Задачи31–40 Исследовать функцию y = f (x) средствами дифференциального исчисления и построить её график. 31. 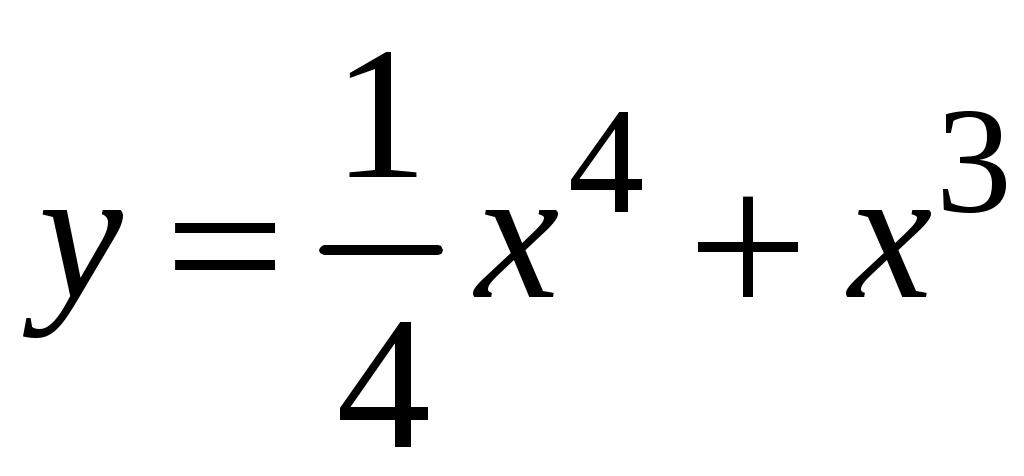 . 32. . 32. 33. 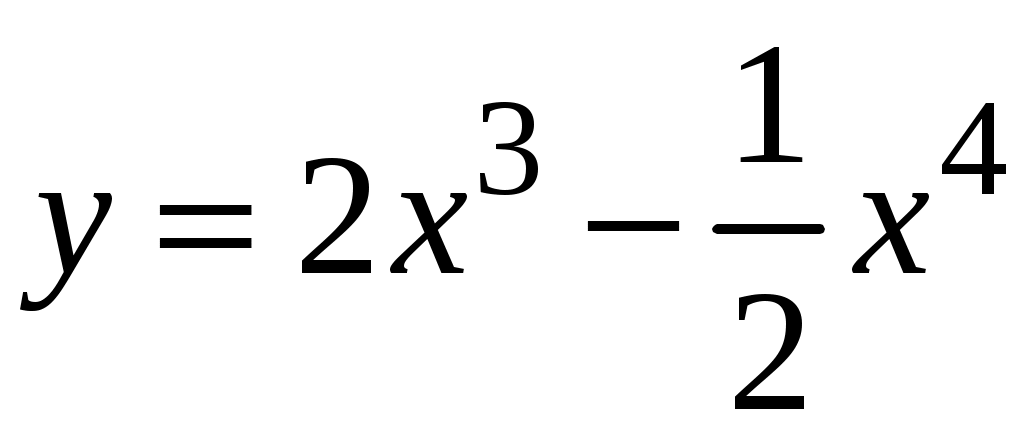 . 34. . 34. 35. 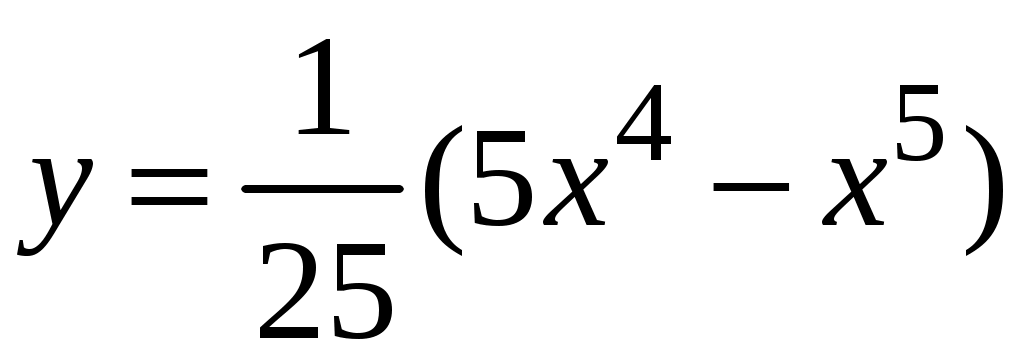 . 36. . 36. 37. 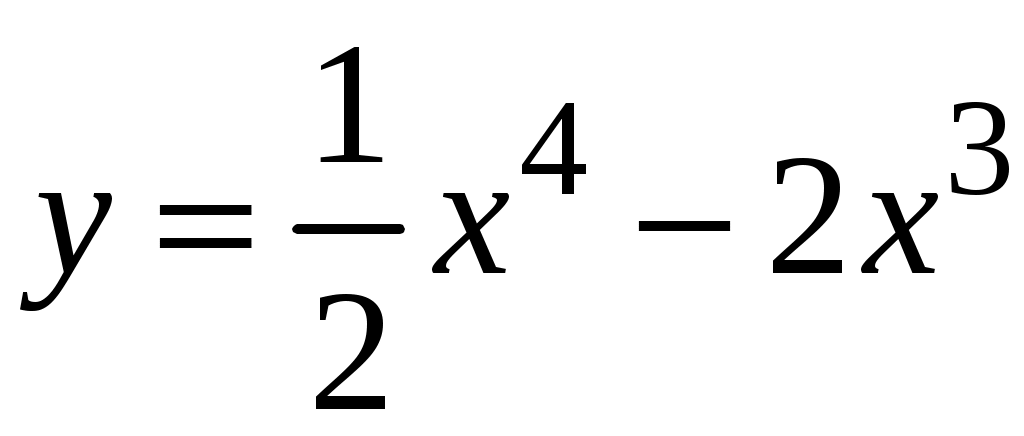 . 38. . 38. 39. 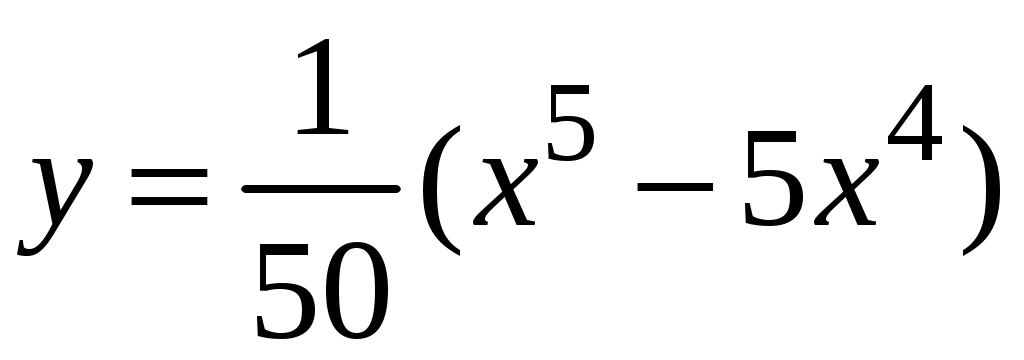 . 40. . 40. Методические указания к решению задач 31 – 40 1. Чётность, нечётность и периодичность функции. Функция y = f(x) называется чётной, если для любых x из области определения функции справедливо равенство f(–x)= f(x), причём область определения также симметрична относительно точки 0, в этом случае график функции симметричен относительно оси Oy. Для нечётной функции для любых x из области определения справедливо равенство f(–x)= – f(x), ее график симметричен относительно начала координат. Функция y = f(x) называется периодической, если существует число Проиллюстрируем на примере некоторые важные свойства графика функции (рис. 2). 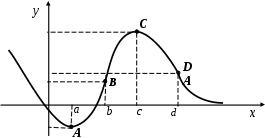 Рис. 2 Интервалы монотонности: функция возрастает при функция убывает при Точки экстремума: С – точка максимума (max); A – точка минимума (min). Интервалы выпуклости и вогнутости: функция выпуклая при функция вогнутая при Точки В иDявляются точками перегиба, так как в них происходит смена выпуклости и вогнутости. 2.Правило исследования функции y = f(x) на монотонность и точки экстремума. а) Вычислить первую производную б) Найти критические точки, то есть точки, в которых производная равна нулю или не существует. в) Определить знак производной на интервалах между критическими точками в области определения функции. г) Сделать выводы о промежутках монотонности функции согласно признакам монотонности: если если д) Сделать выводы о наличии точек экстремума согласно достаточному признаку существования экстремума: если при переходе слева направо через критическую точку 3. Правило исследования функции y = f(x)на выпуклость, вогнутость и точки перегиба. а) Вычислить вторую производную б) Найти точки, в которых вторая производная равна нулю или не существует, эти точки называются подозрительными на перегиб. в) Определить знак второй производной на интервалах между найденными точками в области определения функции. г) Сделать выводы о промежутках выпуклости и вогнутости согласно признакам выпуклости и вогнутости: если если д) Сделать выводы о наличии точек перегиба согласно достаточ-ному условию существования точек перегиба: eсли при переходе через подозрительную на перегиб точку вторая производная меняет знак, то в этой точке имеется перегиб графика функции. |