Математика. Б1.Б.11_ММ Математика 38.03.02. Методические указания и задания к занятиям семинарского типа, контрольной и самостоятельной работе по дисциплине математика
 Скачать 2.28 Mb. Скачать 2.28 Mb.
|
Линейное программированиеЗадачи 111-120 Решить графически задачу линейного программирования (ЛП). 111. 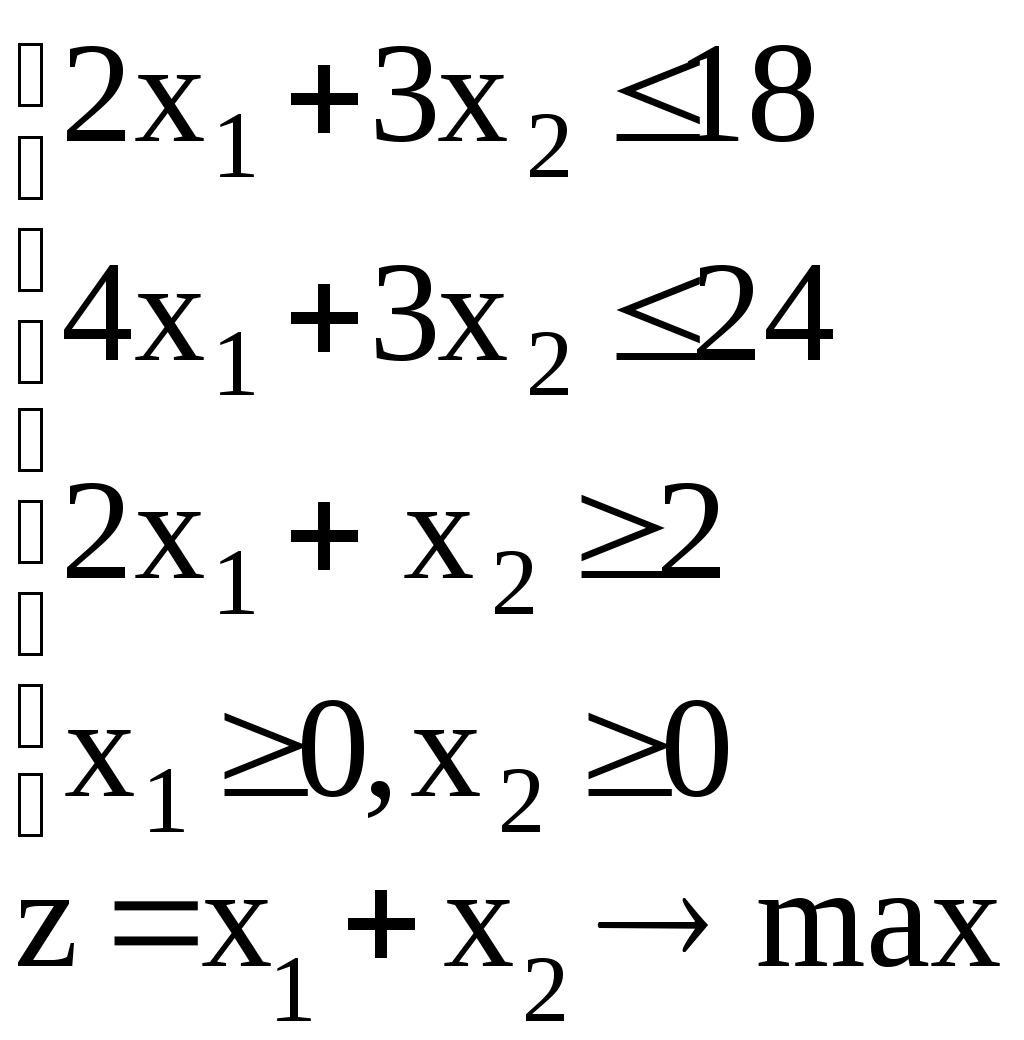 112. 112. 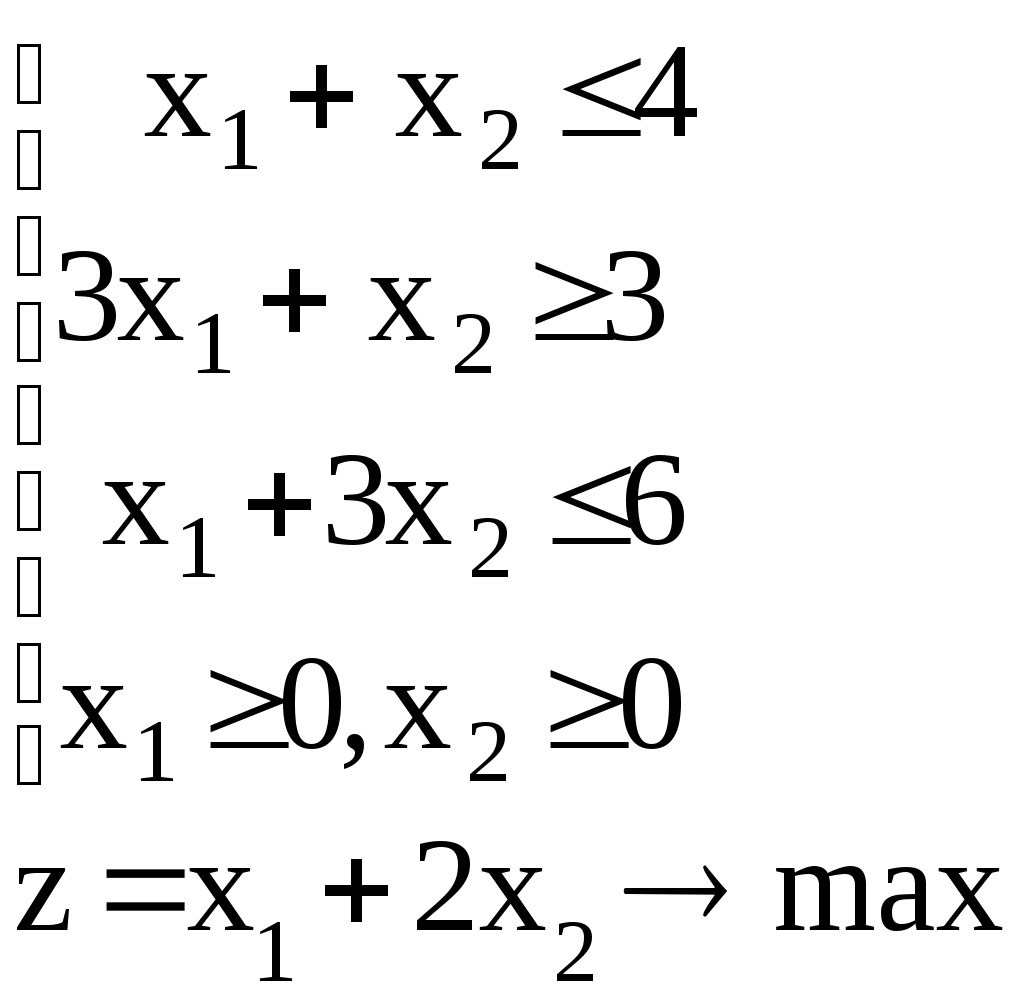 113. 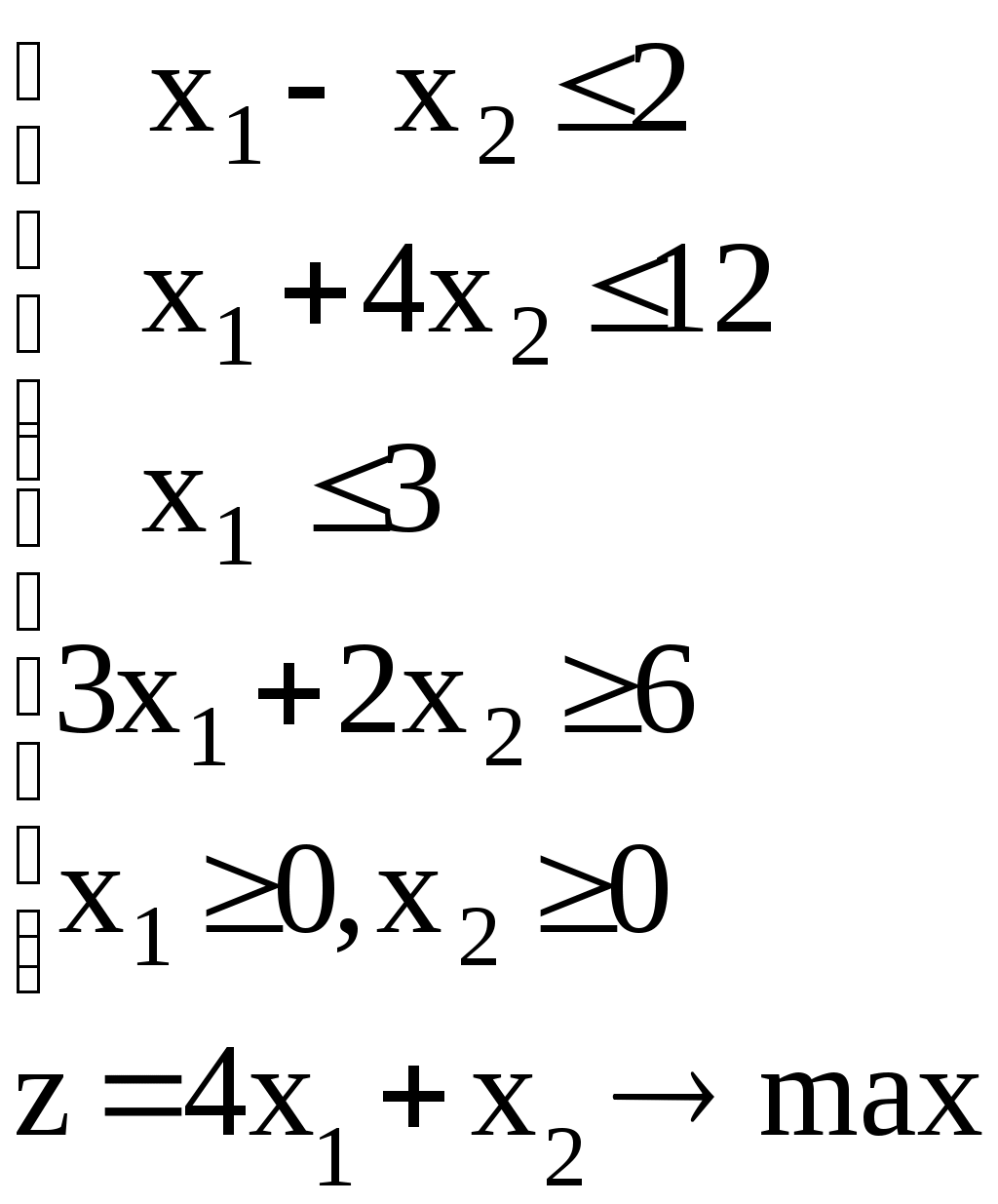 114. 114. 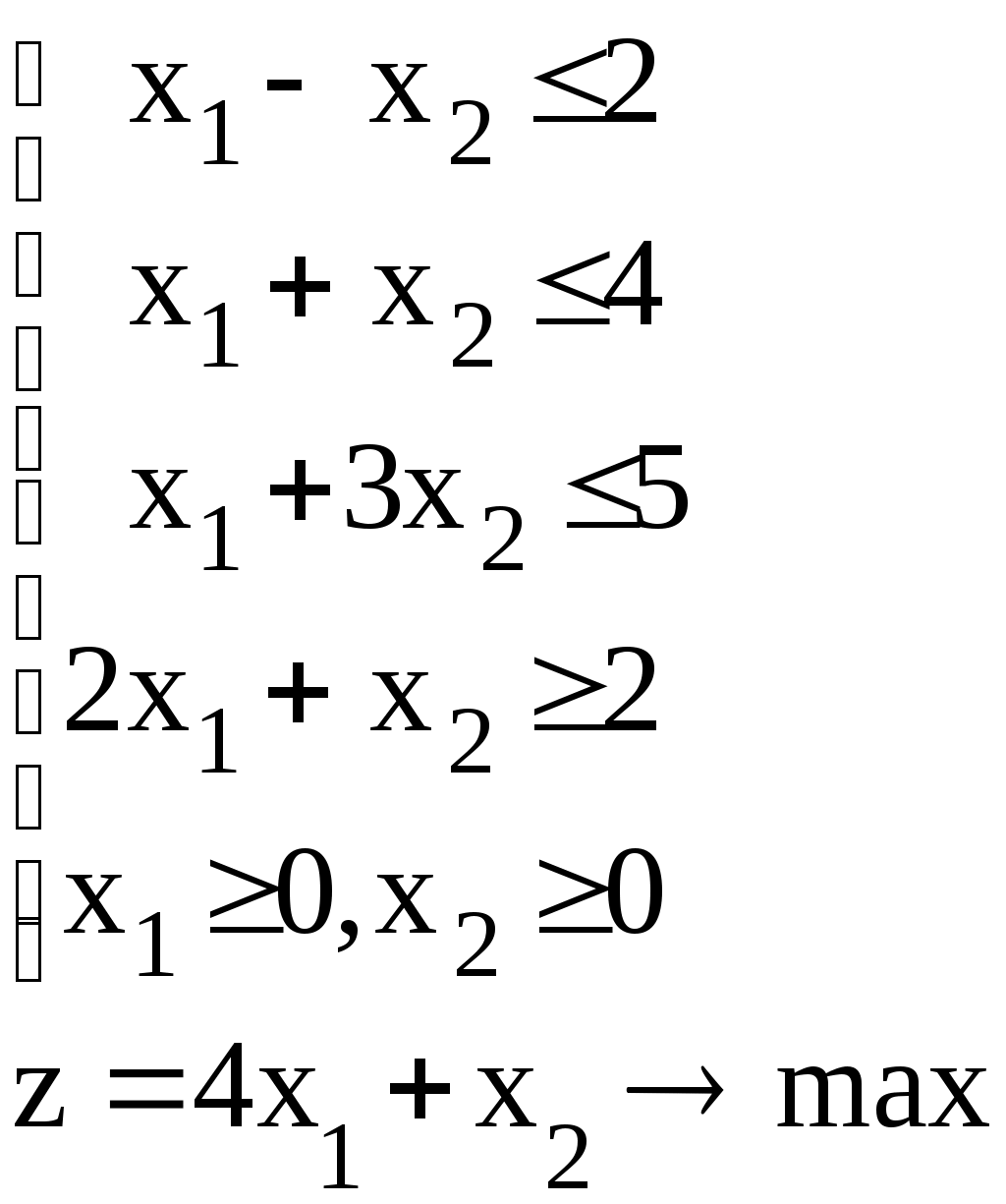 115. 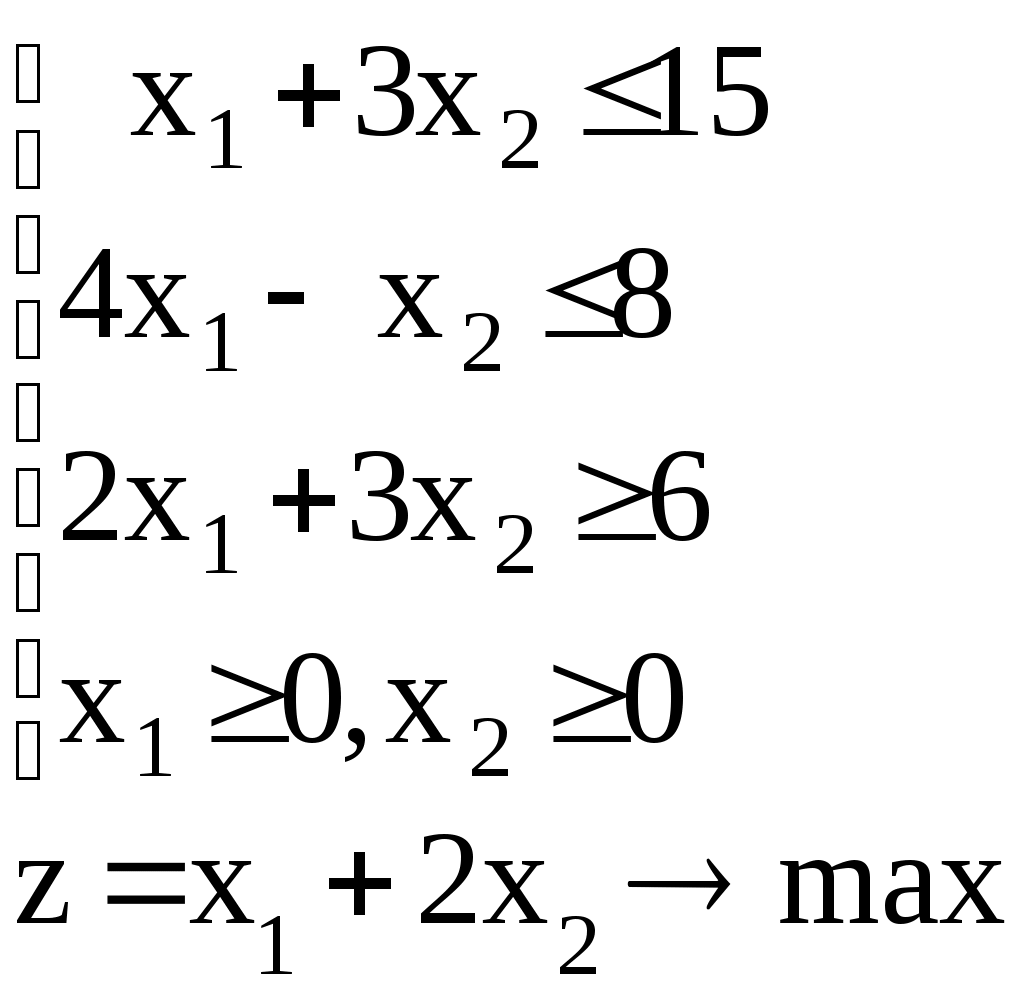 116. 116. 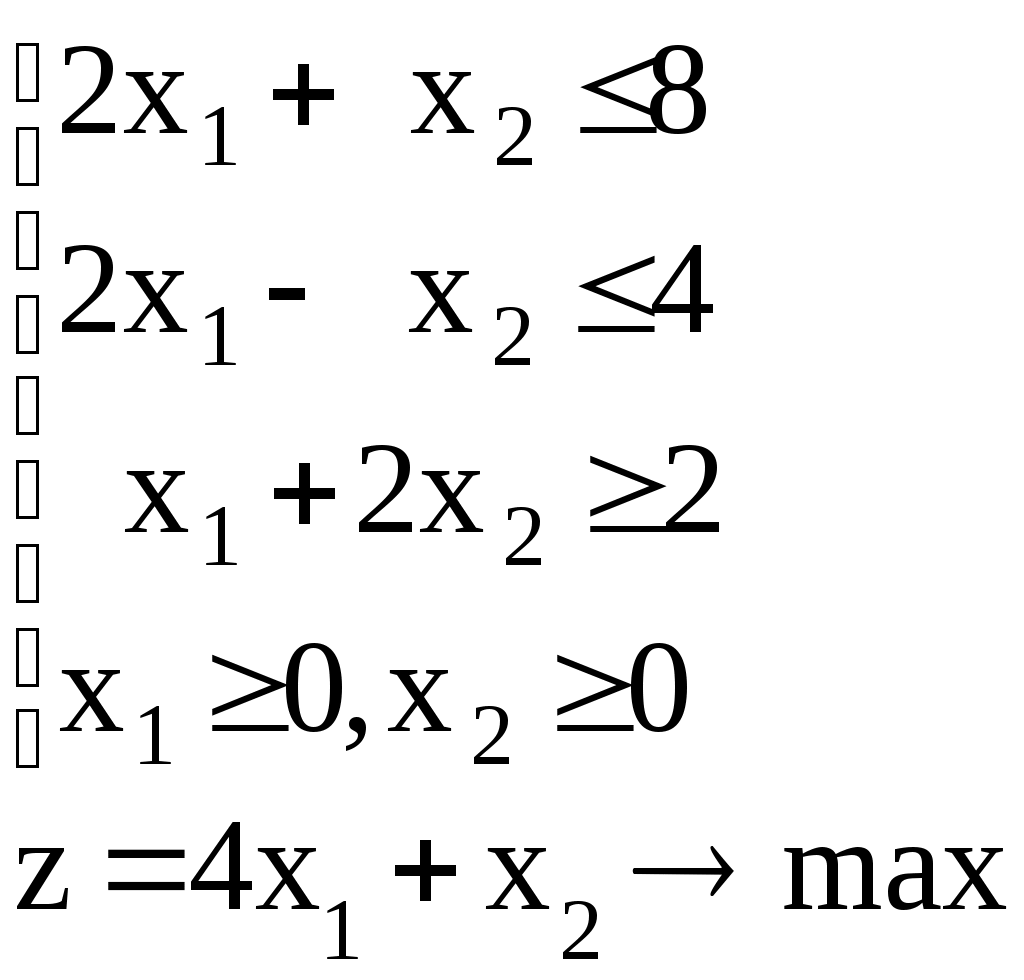 117. 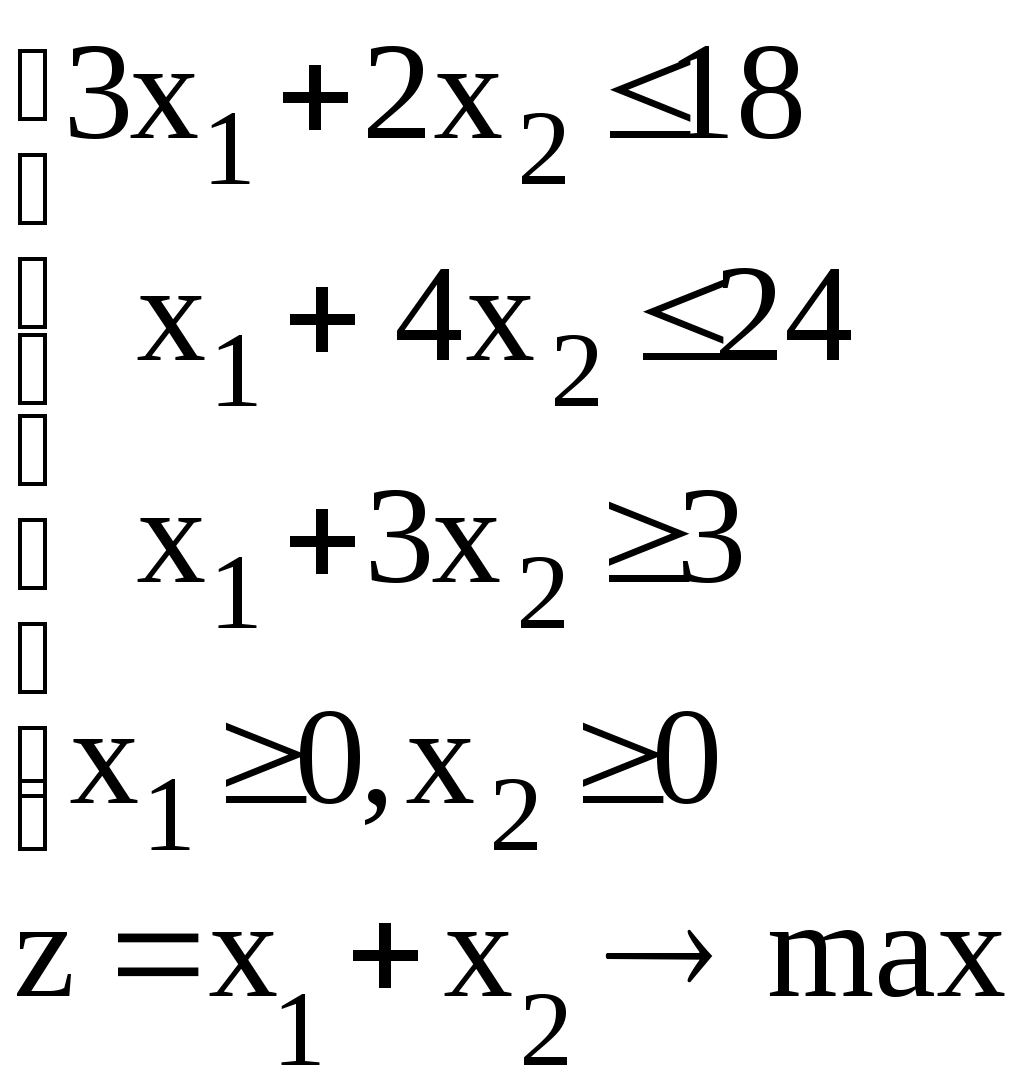 118. 118. 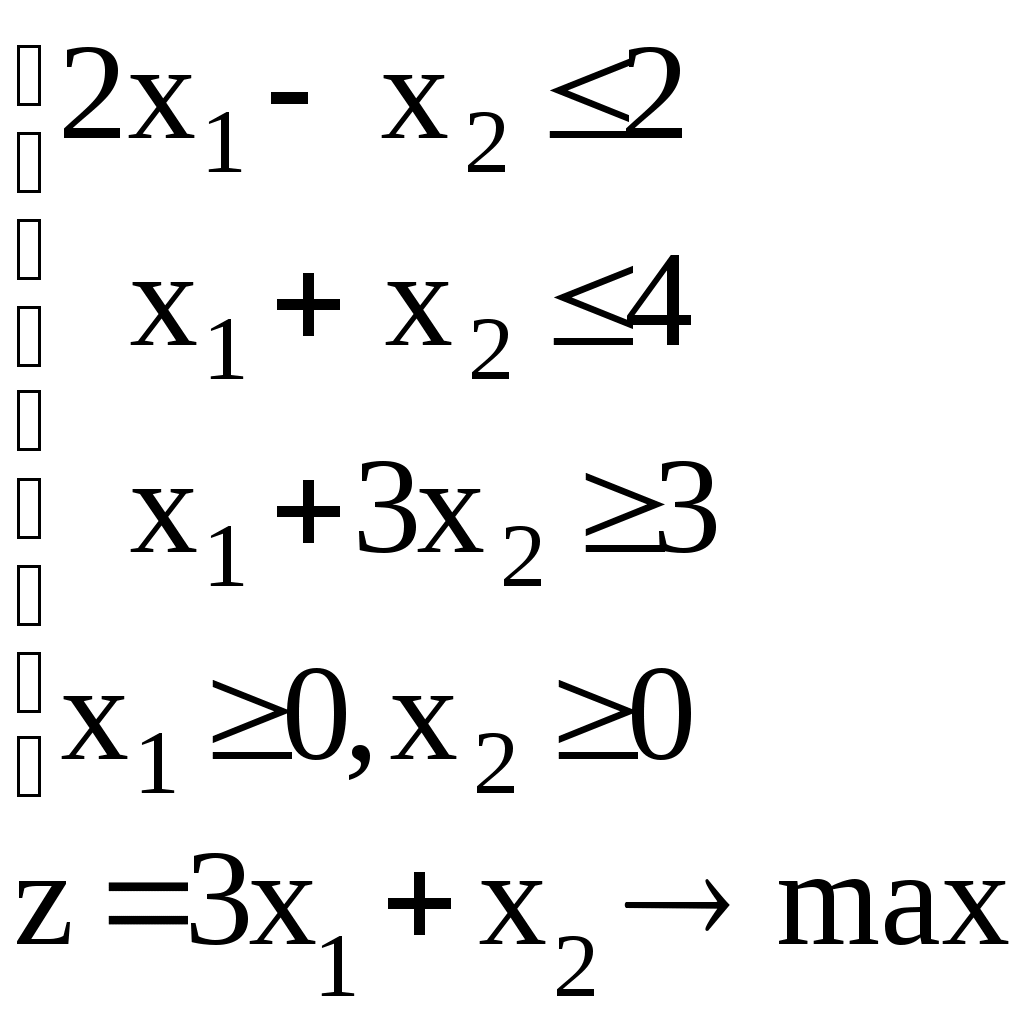 119. 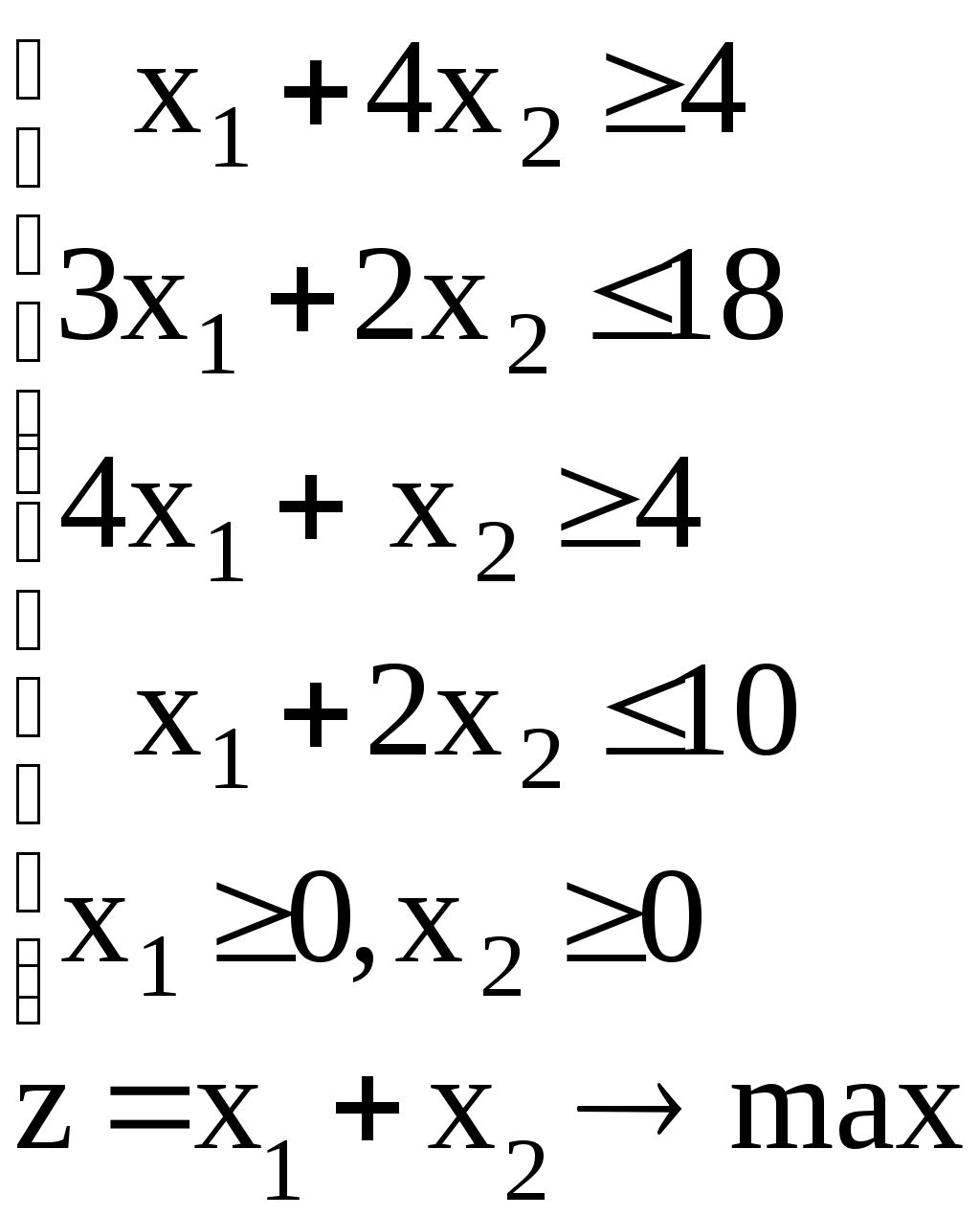 120. 120. 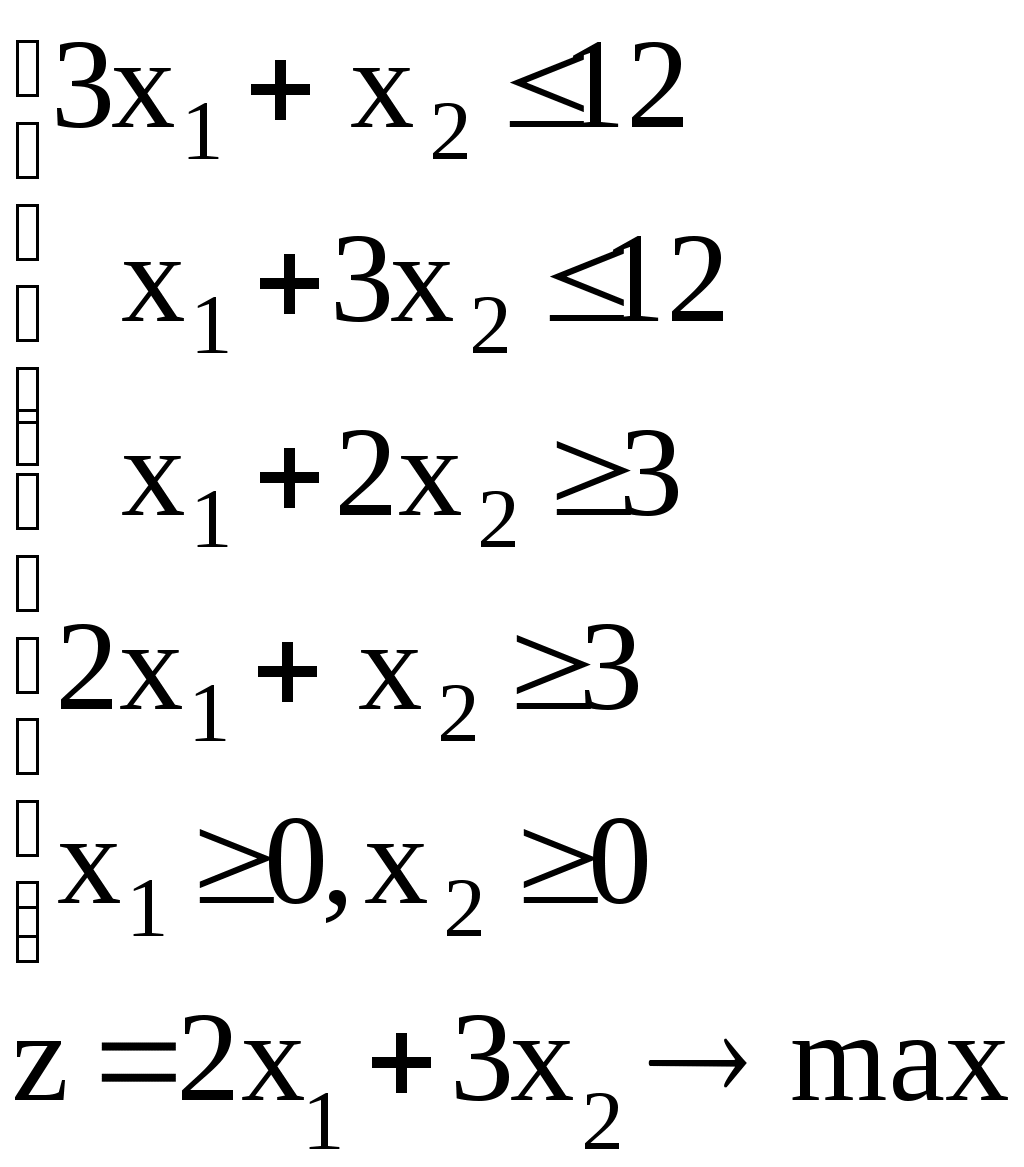 Методические указания к решению задач 111– 120Постановка задачи линейного программированияМногие экономические задачи связаны с нахождением наилучших решений в условиях многочисленных пожеланий и ограничений. Математическое описание таких задач приводит к составлению их математических моделей. Построение математической модели экономической задачи включает следующие этапы: 1). выбор переменных задачи; 2). выбор и составление целевой функции; 3). составление системы ограничений. Переменными задачи называются величины Целевой функцией называют функцию переменных задачи, которая характеризует качество выполнения задачи, и экстремум которой требуется найти. Системой ограничений называют систему уравнений и неравенств, которым должны удовлетворять переменные задачи. Часто рассматривают наиболее простой случай, когда целевая функция и система ограничений являются линейными. В общем виде математическая модель задачи линейного программирования имеет вид: при ограничениях: 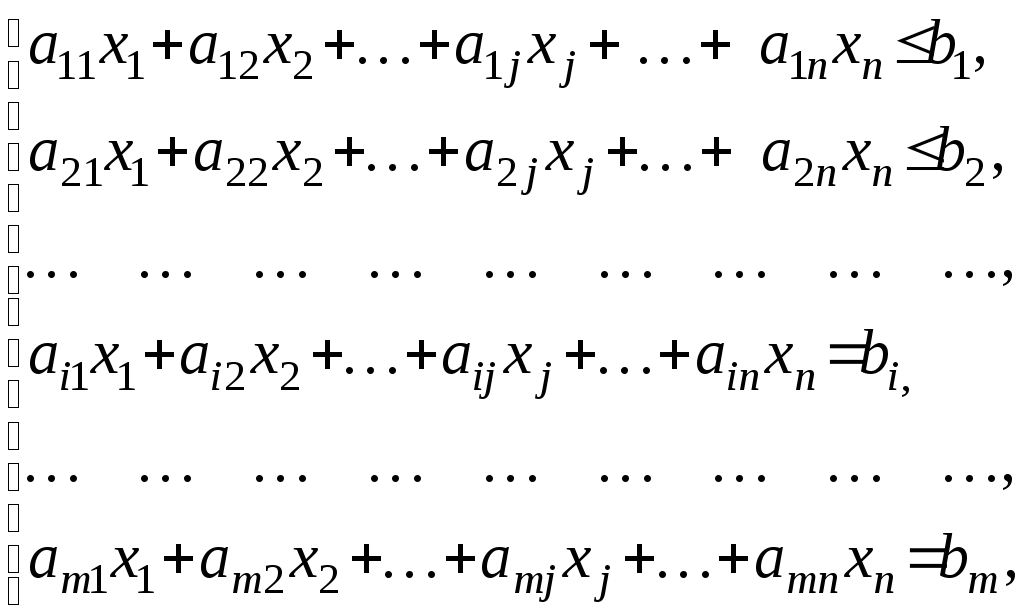 где z = z (x1, x2 ,…, xn) – целевая функция. Допустимым решением (планом) задачи линейного программирования называется совокупность значений переменных х1, х2, …, хn, удовлетворяющая системе ограничений, включая условия неотрицательности переменных. Множество допустимых решений образует область допустимых решений (ОДР). Оптимальным решениемзадачи линейного программирования называется допустимое решение, при котором целевая функция достигает своего экстремального значения (максимума или минимума). Система ограничений задачи может содержать как уравнения, так и неравенства. Однако, ее всегда можно привести к виду, когда система содержит только уравнения (каноническая форма записи) или только неравенства (стандартная форма записи). В настоящее время задачи линейного программирования решаются с помощью компьютерных технологий. Если задача линейного программирования в стандартной форме записи содержит две переменные х1 и х2, то ее можно решить графически. Графический метод решения задачи ЛП Задача. Решить графически задачу линейного программирования z =3х1+4х2 при ограничениях: 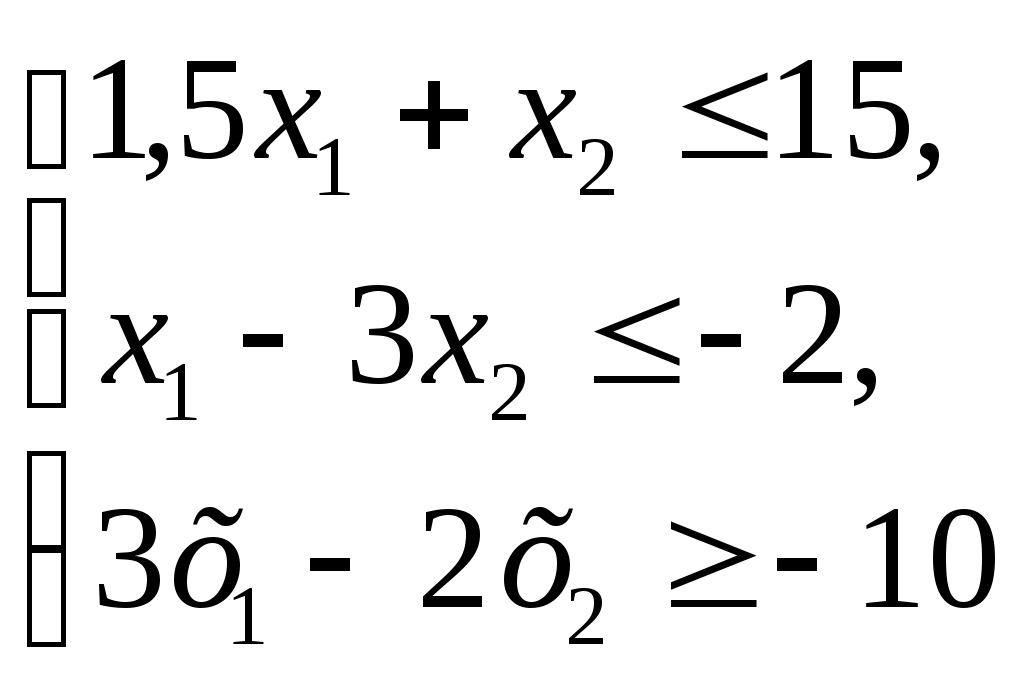 Р ешение: Решение задачи состоит из двух этапов: построение ОДР и нахождения оптимального решения из допустимых. 1). Для построения области допустимых решений изобразим графически множество решений каждого неравенства системы ограничений. a). Рассмотрим первое неравенство: Следовательно, искомая полуплоскость содержит точку (0,0), то есть, выбираем полуплоскость ниже прямой (1). б). Аналогично, находим графически множество решений второго неравенства. Неравенство Следовательно, выбираем полуплоскость, которая не содержит точку (0;0), то есть полуплоскость, расположенную выше прямой (2). с). Далее, множество решений третьего неравенства, Условия неотрицательности Найдем множество точек, лежащих одновременно во всех полуплоскостях и в I-й четверти. В нашей задаче, на рис. 10, это четырехугольник АВСД. Точки, лежащие внутри и на границе этого четырехугольника, и есть допустимые решения задачи, очевидно, что их бесконечно много. 2). Из бесконечного множества допустимых решений нужно выбрать оптимальное. Это делается с помощью целевой функции z =3x1+4x2. На координатной плоскости эту функцию можно изобразить с помощью линий уровня, то есть с помощью линий, на которых значения функции zпостоянны, z = С (const)или 3x1+4x2=С. Графически, линии уровня есть семейство параллельных прямых. Покажем, как построить линии уровня. Если масштабы по осям одинаковые, то построение можно начать с вектора Линии уровня расположены перпендикулярно этому вектору 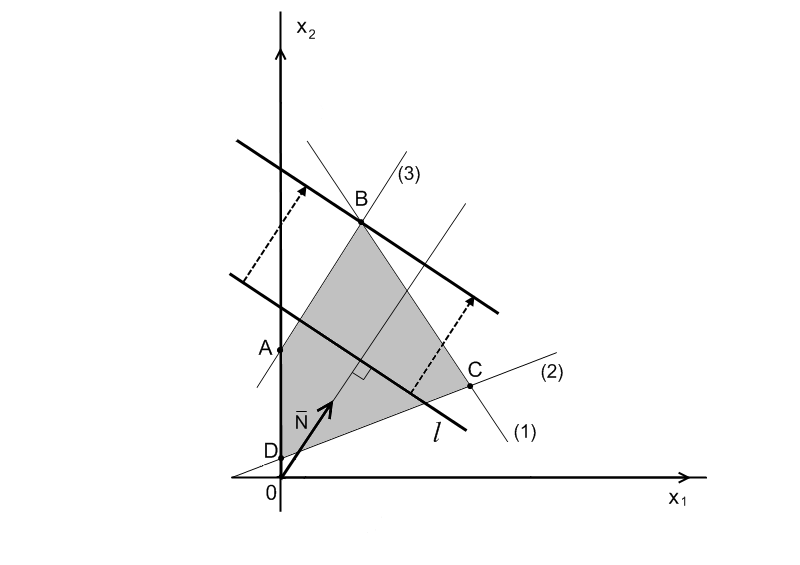 l: 3x1+4x2=C Рис. 10 Далее, перемещаем прямую l по направлению вектора 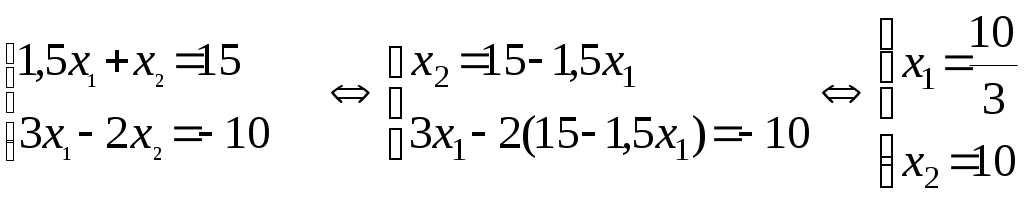 Таким образом найдена точка В(10/3;10). Обратите внимание, что ее координаты должны соответствовать графику. Вычислим максимальное значение целевой функции: zmax = z (B) = Ответ: zmax = 50 при х1=10/3, х2 = 10. Замечание: Для задач на минимум линию уровня перемещаем в направлении, противоположном вектору Если окажется, что линии уровня параллельны одной из сторон ОДР, то в этом случае экстремум достигается во всех точках соответствующей стороны, а задача ЛП будет иметь бесчисленное множество решений. Задача ЛП может быть неразрешима, если ее ограничения окажутся противоречивыми, тогда ОДР есть пустое множество. ЗАДАНИЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ Тема 1. Аналитическая геометрия на плоскости Основные вопросы. 1. Уравнение прямой с угловым коэффициентом. Смысл углового коэффициента, особенности расположения прямой в зависимости от величины углового коэффициента. 2. Общее уравнение прямой и его частные случаи. 3. Условия параллельности и перпендикулярности прямых. Типовые задачи. 1. Построить прямые, заданные уравнениями: а) у = 4 - 2х; б) 3х – 5у + 15 = 0; в) 2у + 5 =0; г) х – 6 = 0; д) 4х – 5у = 0. 2. Найти длину и середину отрезка АВ, если известны точки: А(1;-2) и В(7; 6), сделать чертеж. 3. Найти уравнения прямых, проходящих через точку М(2,-3) параллельно и перпендикулярно прямой 3х – 4у + 12 = 0. 4. Найти уравнение прямой, проходящей через две точки А(4,-1) и В (-5,3), сделать проверку и чертеж. 5. Найти острый угол между прямыми 5х – 2у + 1 = 0 и у = 7 – 3х. 6. Найти расстояние от точки М(-9;5) до прямой у = 3х – 8. Тема 2. Функция и предел функции Основные вопросы. Понятие предела функции в точке и на бесконечности, их графические пояснения. Односторонние пределы. Бесконечно малые и бесконечно большие функции, их свойства и взаимная связь. Первый и второй замечательные пределы. Число е. Определение эквивалентных бесконечно-малых, привести примеры эквивалентных бесконечно-малых. Понятие непрерывности функции в точке. Точки разрыва, их виды. Типовые задачи. 1. Вычислить пределы функций: а) в) д) Исследовать на непрерывность функцию Тема 3. Дифференциальное исчисление и его приложения Основные вопросы. Понятие производной и дифференциала функции. Геометрический, механический и экономический смысл производной. Признаки возрастания и убывания функции. Необходимые и достаточные условия экстремума функции. Признаки выпуклости и вогнутости графика функции. Необходимые и достаточные условия перегиба графика функции. Типовые задачи. 1. Найти производные функций: а) в) 2. Исследовать функции средствами дифференциального исчисления и построить их графики: а) y = x3 - 9x2; б) 3. Составить уравнение касательной, проведенной к графику функции 4. Найти пределы функций по правилу Лопиталя: a) |
