Математика. Б1.Б.11_ММ Математика 38.03.02. Методические указания и задания к занятиям семинарского типа, контрольной и самостоятельной работе по дисциплине математика

• Название: Методические указания и задания к занятиям семинарского типа, контрольной и самостоятельной работе по дисциплине математика
• Анкор: Математика
• Дата: 26.03.2023
• Размер: 2.28 Mb.
• Имя файла: Б1.Б.11_ММ Математика 38.03.02.doc
• Тип: Методические указания; #1015704
• страница: 10 из 10

Тема 14. Повторные независимые испытания

Основные вопросы.

1. 
   Повторение независимых испытаний. Формула Бернулли.
   
2. 
   Наивероятнейшее число появлений события в n испытаниях.
   
3. 
   Локальная и интегральная теоремы Лапласа.
   

Типовые задачи.

1. В магазин поступает натуральный сок в бутылках от двух изготовителей: местного и иногороднего, причем местный изготовитель поставляет 30% всей продукции. Вероятность того, что при транспортировке бутылка окажется разбитой, для местной продукции – 0,6%, а для иногородней – 2%. Найти вероятность того, что взятая наудачу бутылка окажется неразбитой.
2. Оптовая база снабжает товаром n магазинов. Вероятность того, что в течение дня поступит заявка на товар, равна p для каждого магазина. Найти вероятность того, что в течение дня: 1) поступит k заявок; 2) не менее k₁ и не более k₂ заявок; 3) каково наивероятнейшее число поступающих в течение дня заявок и чему равна соответствующая ему вероятность?

а) р = 0,6; n = 7; k = 4; k₁ = 0; k₂ = 2;

б) р = 0,7; n = 20; k = 7; k₁ = 8; k₂ = 14.

Тема 15. Дискретная случайная величина

Основные вопросы.

1. 
   Случайные величины, их виды и способы задания.
   
2. 
   Математическое ожидание и дисперсия дискретной случайной величины.
   
3. 
   Биноминальный закон распределения дискретной случайной величины.
   

Типовые задачи.

1. Найти: математическое ожидание, дисперсию и среднее квадратическое отклонение дискретной случайной величины Х по известному закону ее распределения , заданному таблично:

Х	12	14	18	24	27
Р	0,4	0,3	0,1	0,1	0,1

Тема 16. Непрерывная случайная величина

Основные вопросы.

1. 
   Математическое ожидание и дисперсия непрерывной случайной величины.
   
2. 
   Нормальный закон распределения, показательный и равномерный законы распределения случайной величины.
   
3. 
   Закон больших чисел.
   

Типовые задачи.

1. 
   Коробки с конфетами упаковываются автоматически. Их средняя масса равна 540 г. Известно, что 5 % коробок имеют массу, меньшую 500 г. Вес коробок распределён по нормальному закону. Каков процент коробок, масса которых: а) менее 470 г; б) от 500 до 550 г; в) отличается от средней не более, чем на 30 г?
   

2. 
   Интервал движения автобуса равен 15 минут. Какова вероятность того, что пассажир на остановке автобуса будет ждать его не более 5 минут?
   

Тема 17. Обработка выборочных данных

Основные вопросы.

1. 
   Матричные игры. Равновесная ситуация.
   
2. 
   Основная теорема теории матричных игр.
   
3. 
   Основные свойства оптимальных смешанных стратегий.
   
4. 
   Графический метод решения матричных игр.
   
5. 
   Решение игр с помощью линейного программирования.
   
6. 
   Игры с природой. Игры с нулевой суммой. Кооперативные игры.
   

Типовые задачи.

1. Рассмотреть игру с платежной матрицей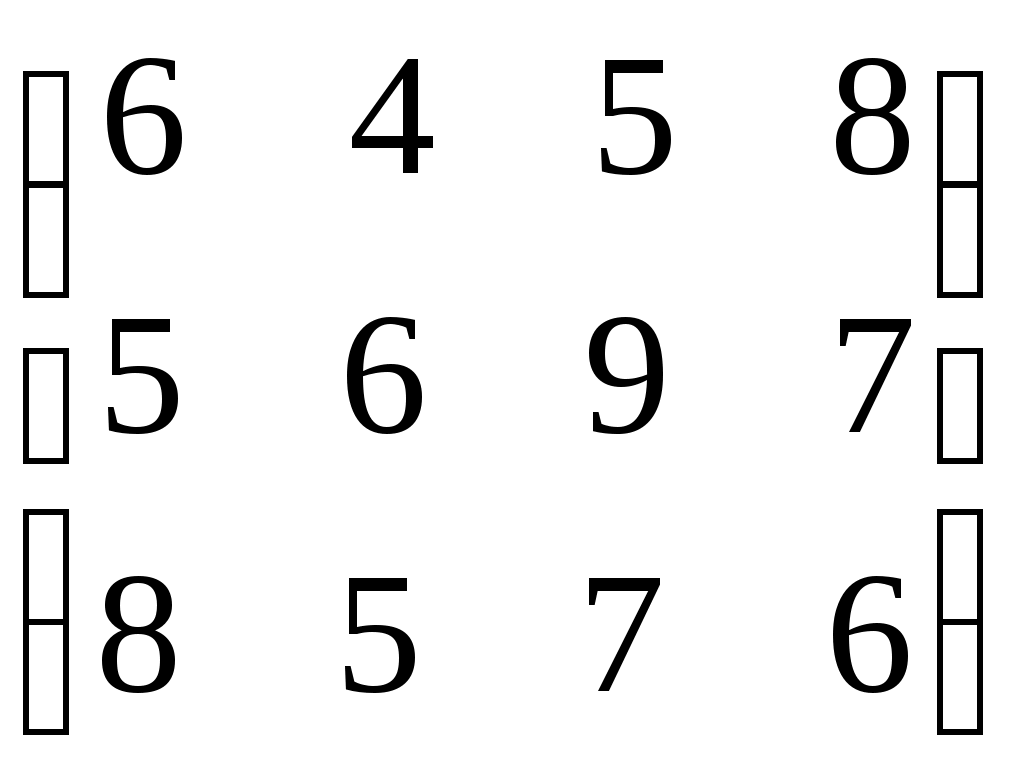

.

Путем исключения недоминирующих стратегий свести эту игру к игре с матрицей , которую решить в смешанных стратегиях.
2. Указать диапазон значений параметра 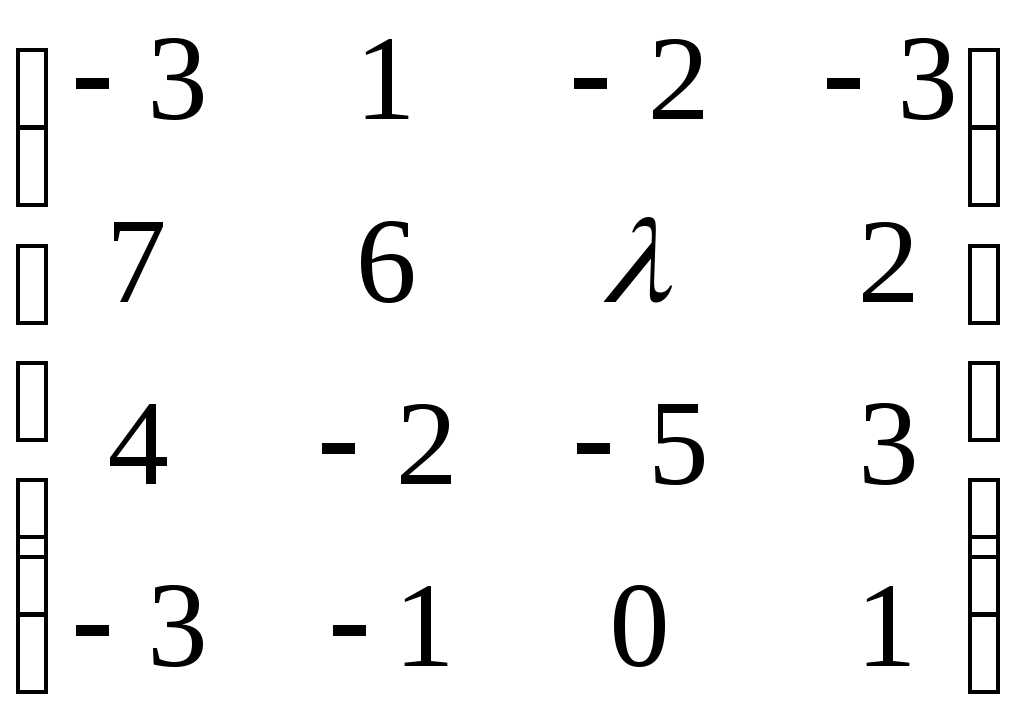, в котором игра имеет седловую точку

.
Тема 18. Проверка статистических гипотез

Основные вопросы.

1. 
   Методы сетевого планирования и управления.
   
2. 
   Графы: плоские, эйлеровы, гамильтоновы, орграфы.
   
3. 
   Сетевые графики. Правила построения сетевых графиков.
   
4. 
   Сети Петри.
   
5. 
   Временные параметры сетевых графиков.
   
6. 
   Коэффициент напряженности работы.
   
7. 
   Анализ и оптимизация сетевого графика.
   

Типовые задачи.

1. Нарисовать граф, соответствующий матрице А: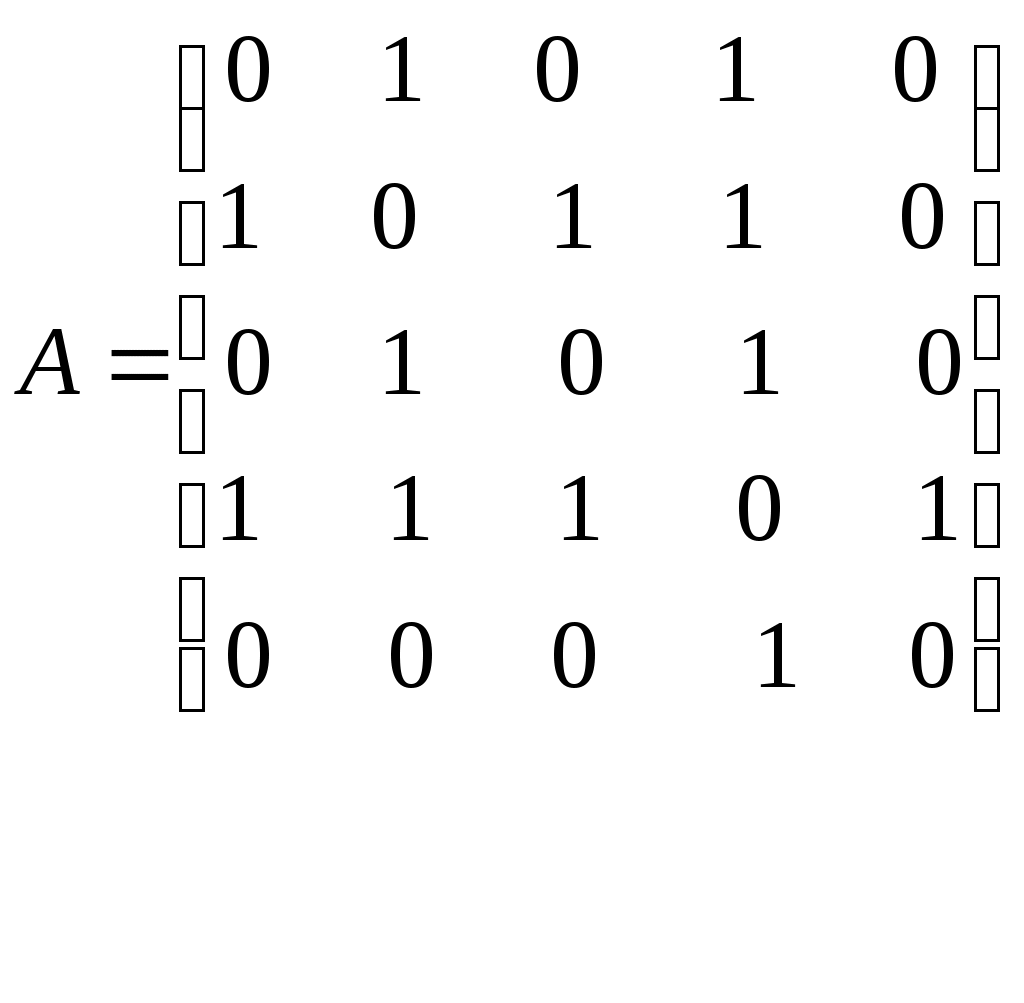



Тема 19. Теория корреляции

Основные вопросы.

1. 
   Системы массового обслуживания.
   
2. 
   Марковский случайный процесс.
   
3. 
   Потоки событий.
   
4. 
   СМО с отказами.
   
5. 
   СМО с неограниченным ожиданием.
   
6. 
   СМО с ожиданием и с неограниченной длиной очередью.
   
7. 
   Определение эффективности использования трудовых и производственных ресурсов в СМО.
   

Типовые задачи.

1. В порту имеется один причал для разгрузки судов. Интенсивность потока судов составляет 0,4 судна в сутки. Интенсивность разгрузки судов составляет 0,5 судна в сутки. Предполагается, что очередь может быть неограниченной длины. Определить показатели эффективности работы причала и вероятность того, что ожидают разгрузки не более двух судов.

4. СПИСОК РЕКОМЕНДОВАННОЙ ЛИТЕРАТУРЫ

Основная учебная литература 1 Бортаковский А. С. Линейная алгебра и аналитическая геометрия. Практикум: учебное пособие для вузов / А. С. Бортаковский, А. В. Пантелеев. - М.: Инфра-М, 2017. – 352 с.: ил. - (Высшее образование: Бакалавриат). - Библиогр.: с. 346. - ISBN 978-5-16-010206-1. - ISBN 978-5-16-102079-1. 2 Высшая математика: учебник / В.С. Шипачев. — М.: ИНФРА-М, 2017. — 479 с. — (Высшее образование). — www.dx.doi.org/10.12737/5394. - Ре-жим доступа: http://znanium.com/go.php?id=851522. 3 Теория вероятностей и математическая статистика: Учебное пособие / Л.Г. Бирюкова, Г.И. Бобрик, В.И. Матвеев, - 2-е изд. – М.: НИЦ ИНФРА-М, 2017. - 289 с.: 60x90 1/16. - (Высшее образование: Бакалавриат) (Переплёт 7БЦ) ISBN 978-5-16-011793-5. - Режим доступа: http://znanium.com/go.php?id=370899. Дополнительная учебная литература 4 Высшая математика: Практикум / И.Г. Лурье, Т.П. Фунтикова. - М.: Вузовский учебник: НИЦ ИНФРА-М, 2013. - 160 с.: 60x88 1/16. (обложка) ISBN 978-5-9558-0281-7, 200 экз. - Режим доступа: http://znanium.com/go.php?id=368074. 5 Математический анализ: сборник задач к практическим занятиям и самостоятельной работе студентов / сост.: С.Г. Бугаева, Н.Г. Орлова; ЧОУ ВО Центросоюза РФ СибУПК. - Новосибирск, 2016. - 88с. : ил. - Библиогр.:с.87. 6 Математический анализ для экономистов: практикум: Учебное пособие/ Т.И. Демина, О.П. Шевякова - М.: НИЦ ИНФРА-М, 2016. - 365 с.: 60x90 1/16. - (Высшее образование: Бакалавриат) (Переплёт) ISBN 978-5-16-010388-4, 500 экз. - Режим доступа: http://znanium.com/go.php?id=486418. 7 Теория вероятностей и математическая статистика: учебник / Е.С. Кочетков, С.О. Смерчинская, В.В. Соколов. — 2-е изд., испр. и перераб. — М.: ФОРУМ : ИНФРА-М, 2018. — 240 с. — (Среднее профессиональное образование). - Режим доступа: http://znanium.com/go.php?id=944923.
5. ПЕРЕЧЕНЬ СОВРЕМЕННЫХ ПРОФЕССИОНАЛЬНЫХ БАЗ ДАННЫХ И ИНФОРМАЦИОННЫХ СПРАВОЧНЫХ СИСТЕМ
			- Mathcad-справочник по высшей математике - http:// www.exponenta.ru/soft/Mathcad/learn/learn.asp - Научная электронная библиотека: www.elibrary.ru - Общероссийский математический портал (информационная система) - http://www.mathnet.ru/ - Электронно-библиотечная система: www.znanium.com
6. УЧЕБНО-МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ
№ п/п Темы дисциплины Перечень учебно-методических материалов 1 Аналитическая геометрия на плоскости. 1,2 2 Функция и предел функции. 2,4,5 3 Дифференциальное исчисление и его приложения. 2,4,6 4 Интегральное исчисление и его приложения. 2,4,5,6 5 Дифференциальные уравнения. 2,4,6 6 Аналитическая геометрия в пространстве 1,2,6 7 Функции нескольких переменных. 1,4,5 8 Матрицы. 1,2,6 9 Система линейных алгебраических уравнений. 1,2,4 10 Задачи линейного программирования. 3,4 11 Транспортная задача линейного программирования 2,3,4 12 Оптимизационные задачи. 2,3,4,6 13 Основные понятия и теоремы теории вероятностей. 4,6,7 14 Повторные независимые испытания. 4,6,7 15 Дискретная случайная величина. 4,7 16 Непрерывные случайные величины. 2,4,7 17 Обработка выборочных данных. 3,4,7 18 Проверка статистических 3,4,7 19 Теория корреляции 4,7