Ауе. Основное 4 МУ АД Лаб 4 сем (1). Методические указания к проведению лабораторных занятий по нормативной учебной дисциплине естественнонаучного цикла Анализ данных
 Скачать 6.5 Mb.
|
|
2. КЛАССИФИЦИРУЮЩИЕ ФУНКЦИИ До сих пор мы рассматривали получение канонических дискриминантных функций при известной принадлежности объектов к тому или иному классу. Основное внимание уделялось определению числа и значимости этих функций, и использованию их для объяснения различий между классами. Все сказанное относилось к интерпретации результатов ДА. Однако наибольший интерес представляет задача предсказания класса, которому принадлежит некоторый случайно выбранный объект. Эту задачу можно решить, используя информацию, содержащуюся в дискриминантных переменных. Существуют различные способы классификации. В процедурах классификации могут использоваться как сами дискриминантные переменные так и канонические дискриминантные функции. В первом случае применяется метод максимизации различий между классами для получения функции классификации, различие же классов на значимость не проверяется и, следовательно, дискриминантный анализ не проводится. Во втором случае для классификации используются непосредственно дискриминантные функции и проводится более глубокий анализ. 2.1. Применение элементарных классифицирующих функций Рассмотрим случай отнесения случайно выбранного объекта  к одной из групп  . Пусть  плотность распределения х в  и  априорная вероятность того, что вектор х принадлежит к группе . Предполагается, что сумма априорных вероятностей  равна 1. Определим условную вероятность  получения некоторого вектора х, если известно, что объект принадлежит к группе  . Обозначим через  условную вероятность принадлежности объекта к группе при заданном х. Величины и называются апостериорными вероятностями. Различие между априорными и апостериорными вероятностями заключается в следующем. Априорная вероятность  равна вероятности принадлежности объекта к данной группе до получения вектора наблюдений х. Апостериорная вероятность определяет вероятность принадлежности объекта к группе только после анализа вектора наблюдений х этого объекта.Из теоремы Байеса получаем  . (17)Выражение (17) справедливо для любого распределения вектора х. Байесовская процедура минимизирует ожидаемую вероятность ошибочной классификации 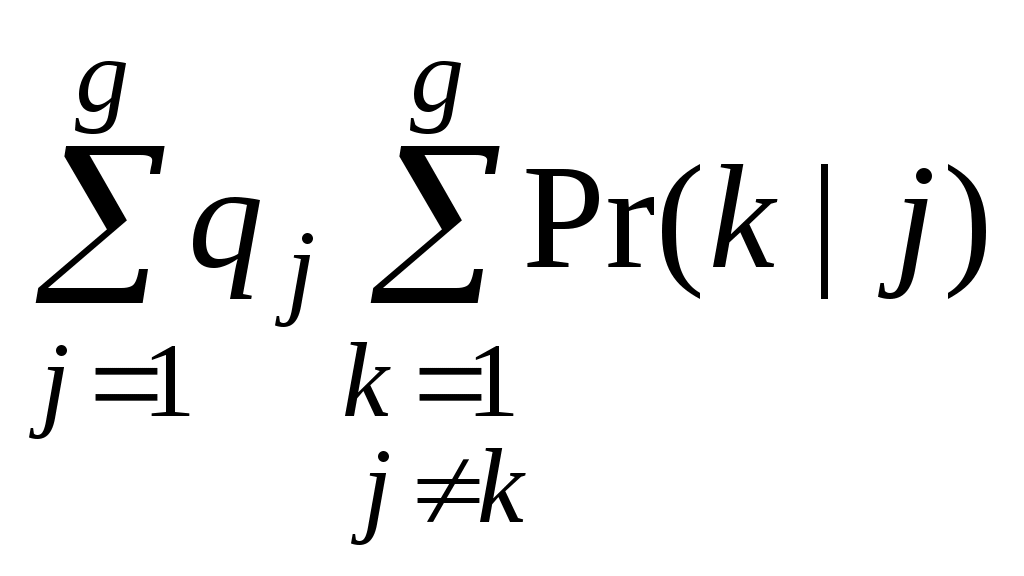 .Так, например, для двух групп получим  .Эта величина является вероятностью того, что объект, принадлежащий к группе  , ошибочно классифицируется, как принадлежащий  , или наоборот, объект из ошибочно относится к .Если х имеет p-мерный нормальный закон распределения  , то вероятности  можно заменить соответственно на плотности распределений  . В результате получим . (18)Байесовская процедура классификации состоит в том, что вектор наблюдений х относится к группе , если имеет наибольшее значение.Можно показать, что байесовская процедура эквивалентна отнесению вектора х к группе , если оценочная функция (19)является максимальной. Подставим в оценочную функцию (19) формулу нормального закона распределения  .Удаляя общую константу  и логарифмируя, получим . (20)Преобразуем выражение (20)  и, удалив постоянную  , получим .Заменим векторы средних и ковариационную матрицу их оценками  и Σ. Тогда получим классифицирующую функцию вида . (21)Введем обозначения  и  ,  ,где  и  – коэффициенты k-й классифицирующей функцииi-го объекта (простой дискриминантной функции Фишера) . (22)Объект  относится к классу, у которого значение d оказывается наибольшим. Коэффициенты классифицирующих функций удобнее вычислять по скалярным выражениям , (23)где  коэффициент для переменной i в выражении, соответствующему классу k,  обратный элемент внутригрупповой матрицы сумм попарных произведений W. Постоянный член находится по формуле . (24)Функции, определяемые соотношением (22), называются «простыми классифицирующими функциями» потому, что они предполагают лишь равенство групповых ковариационных матриц и не требуют других дополнительных свойств. 2.2. Классификация объектов с помощью функции расстояния Выбор функций расстояния между объектами для классификации является наиболее очевидным способом введения меры сходства для векторов объектов, которые интерпретируются как точки в евклидовом пространстве. В качестве меры сходства можно использовать евклидово расстояние между объектами. Чем меньше расстояние между объектами, тем больше сходство. Однако в тех случаях, когда переменные коррелированы, измерены в разных единицах и имеют различные стандартные отклонения, трудно четко определить понятие «расстояния». В этом случае полезнее применить не евклидовое расстояние, а выборочное расстояние Махаланобиса  (25)или в матричной записи  , (25׳)где х представляет объект с р переменными,  -вектор средних для переменных k-й группы объектов. Если вместо  использовать оценку внутригрупповой ковариационной матрицы   , то получим стандартную запись выборочного расстояния Маханалобиса . (26)При использовании функции расстояния, объект относят к той группе, для которой расстояние  наименьшее. Относя объект к ближайшему классу в соответствии с , мы неявно приписываем его к тому классу, для которого он имеет наибольшую вероятность принадлежности  . Если предположить, что любой объект должен принадлежать одной из групп, то можно вычислить вероятность его принадлежности для любой из групп . (27)Объект принадлежит к той группе, для которой апостериорная вероятность максимальна, что эквивалентно использованию наименьшего расстояния. До сих пор при классификации по предполагалось, что априорные вероятности появления групп одинаковы. Для учета априорных вероятностей нужно модифицировать расстояние , вычитая из выражений (25)–(26) удвоенную величину натурального логарифма от априорной вероятности . Тогда, вместо выборочного расстояния Махаланобиса (26), получим  . (28)Это изменение расстояния математически идентично умножению величин  на априорную вероятность группы . Формулу (28) можно получить, умножив правые и левые части выражения (20) на два. Тогда после замены векторов средних и ковариационной матрицы их оценками имеем  .Отметим, тот факт, что априорные вероятности оказывают наибольшее влияние при перекрытии групп и, следовательно, многие объекты с большой вероятностью могут принадлежать ко многим группам. Если группы сильно различаются, то учет априорных вероятностей практически не влияет на результат классификации, поскольку между классами будет находиться очень мало объектов. V-статистика Рао. В некоторых работах для классификации используется обобщенное расстояние Махаланобиса V – обобщение величины . Эта мера, известная как V-статистика Рао, измеряет расстояния от каждого центроида группы до главного центроида с весами, пропорциональными объему выборки соответствующей группы. Она применима при любом количестве классов и может быть использована для проверки гипотезы  . Если гипотеза  верна, а объемы выборок  стремятся к ∞, то распределение величины V стремится к  с  степенями свободы. Если наблюдаемая величина  , то гипотеза отвергается. V-статистика вычисляется по формуле . (29)Матричное выражение оценки Vимеет вид  . (30)Отметим, что при включении или исключении переменных V-статистика имеет распределение хи-квадрат с числом степеней свободы, равным (g - 1), умноженное на число переменных, включенных (исключенных) на этом шаге. Если изменение статистики не значимо, то переменную можно не включать. Если после включения новой переменной V-статистика оказывается отрицательной, то это означает, что включенная переменная ухудшает разделение центроидов. 2.3. Классификационная матрица В дискриминантном анализе процедура классификации используется для определения принадлежности к той или иной группе случайно выбранных объектов, которые не были включены при выводе дискриминантной и классифицирующих функций. Для проверки точности классификации применим классифицирующие функции к тем объектам, по которым они были получены. По доле правильно классифицированных объектов можно оценить точность процедуры классификации. Результаты такой классификации представляют в виде классификационной матрицы. Рассмотрим пример классификационной матрицы, приведенной в табл. 1. Таблица 1 Классификационная матрица
В первой группе точно предсказаны из 10 объектов 9, что составляет 90 %, один объект отнесен к 4-й группе. Во второй группе правильно предсказаны 80 % объектов, один объект (20 %) отнесен к третьей группе. В третьей группе процент правильного предсказания самый низкий и составляет 68,5 %, причем из 54 объектов 8 отнесены к первой группе, 4 – ко второй и 5 – к четвертой группе. В четвертой группе правильно предсказаны 84,6%, по одному объекту отнесено к первой и третьей группам. Процент правильной классификации объектов является дополнительной мерой различий между группами и ее можно считать наиболее подходящей мерой дискриминации. Следует отметить, что величина процентного содержания пригодна для суждения о правильном предсказании только тогда, когда распределение объектов по группам производилось случайно. Например, для двух групп при случайной классификации можно правильно предсказать 50 %, а для четырех групп эта величина составляет 25 %. Поэтому если для двух групп имеем 60 % правильного предсказания, то нужно считать эту величину слишком малой, тогда как для четырех групп эта величина говорит о хорошей разделительной способности. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||