Ауе. Основное 4 МУ АД Лаб 4 сем (1). Методические указания к проведению лабораторных занятий по нормативной учебной дисциплине естественнонаучного цикла Анализ данных
 Скачать 6.5 Mb. Скачать 6.5 Mb.
|
|
Пример. Больные гипертиреозом (увеличение щитовидной железы) общим числом 23 человека были разделены на три группы. Группа 1. Лечение оказалось успешным; проведенное через большой промежуток времени клиническое обследование показало, что пациент здоров. Группа 2. Лечение безуспешно, т. е. состояние больного осталось без изменения. Группа 3. Исход лечения успешен, но в дальнейшем возможен рецидив. По результатам обследования 23 пациентов имеются следующие измерения: y6 – йод, регистрируемый через 3 часа после принятия испытательной дозы; y9 – йод, регистрируемый через 48 часов после принятия испытательной дозы; y10 – содержание в крови белковосвязанного йода (РВ131J) через 48 часов; kl – номер группы. Конкретные результаты приведены в табл.2. Таблица 2 Данные о 23 больных гипертиреозом, разделенныз на три группы
По матрице исходных данных находятся средние и стандартные отклонения дискриминантных переменных (табл. 3, 4), общая T и внутригрупповые W матрицы сумм квадратов и перекрестных произведений (табл. 5, 6). Таблица 3 Средние дискриминантных переменных
Таблица 4 Стандартные отклонения
Таблица 5 Матрица общей суммы перекрестных произведений Т
Таблица 6 Матрица внутригрупповой суммы перекрестных произведений W
Если разделить каждый элемент T на (n - 1)), а каждый элемент W – на (n – g), то получим ковариационные матрицы. Для оценки меры связи между дискриминантными переменными матрицы T и W преобразованы в корреляционные матрицы, которые приведены в табл. 7 и 8. Элементы этих матриц найдены по формулам Из общей корреляционной матрицы видно, что переменные некоррелированы на уровне 0.01. Отсюда следует, что ни одна переменная не может быть предсказана по значению, соответствующему другой переменной. Таблица 7 Общая корреляционная матрица
Для измерения меры разброса наблюдений внутри классов используется внутригрупповая корреляционная матрица, которая приведена в табл. 8. Эта матрица не совпадает с общей корреляционной матрицей. Из таблицы видно, что многие коэффициенты отличаются от значений, приведенных в табл.7. Таблица 8 Внутригрупповая корреляционная матрица
Из табл. 5 и 6 видно, что большая часть элементов матрицы W меньше соответствующих элементов матрицы T. Разница этих матриц Таблица 9 Матрица межгрупповой суммы перекрестных произведений B
Для нахождения коэффициентов канонической дискриминантной функции решаем задачу (2) в терминах собственных чисел и векторов, которая в матричной записи имеет вид (10). Систему уравнений (10) решаем с помощью разложения Холецкого матрицы 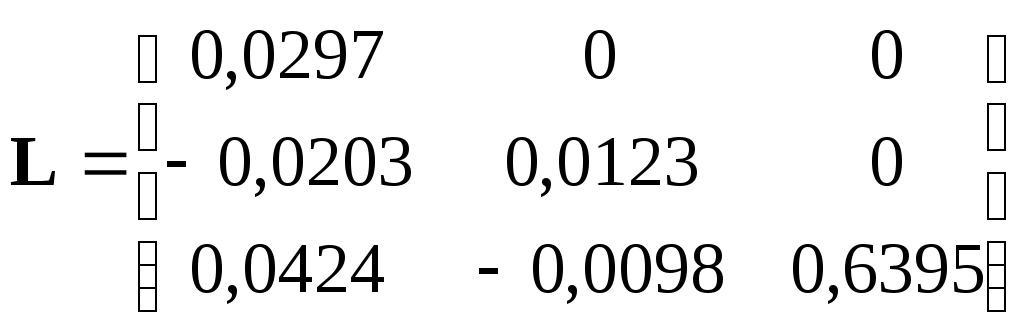 Наибольшее собственное значение для системы равно При использовании коэффициентов b начало координат не будет совпадать с главным центроидом. Для того чтобы начало координат совпало с главным центроидом нужно нормировать компоненты вектора b, используя формулы (11). Для оценки относительного вклада каждой переменной в значение дискриминантной функции вычислим стандартизованные дискриминантные коэффициенты по формуле (12). Результаты вычислений приведены в табл.10. Из табл.10 видно, что две наиболее значимо коррелированные переменные Y6 и Y9 имеют примерно одинаковые стандартизованные коэффициенты. Значения нестандартизованной канонической функции для каждого пациента сведены в табл.15. Координаты центроидов первой, второй и третьей групп соответственно равны: Таблица 10 Коэффициенты дискриминантной функции
Для определения взаимной зависимости отдельной переменной и дискриминантной функции рассмотрим внутригрупповые структурные коэффициенты, значения которых находим по формуле (13). Результаты вычислений представлены в табл. 11. Таблица 11 Внутригрупповые структурные коэффициенты
Переменные Y6 и Y9 имеют небольшие структурные коэффициенты, но у них относительно большие стандартизованные коэффицинты. Это объясняется значимой корреляцией переменной Y6 с другими переменными и может оказаться, что вклад переменных Y6 и Y9 в дискриминантые значения невелик. Для оценки реальной полезности канонической дискриминантной функции вычисляем по формулам (14)–(16) коэффициент канонической корреляции, Λ-статистику Уилкса , статистику хи-квадрат, уровень значимости. Результаты вычислений приведены в табл. 12. Таблица 12 Основные статистики
Данные таблицы указывают на хорошую дискриминацию групп: большая величина канонической корреляции соответствует тесной связи дискриминантной функции с группами; малая величина Λ-статистики Уилкса означает, что четыре используемых переменных эффективно участвуют в различении групп и, наконец, статистика хи-квадрат значима с уровнем 1,6 10-8. Процедура классификации. Процедуры классификации могут использовать канонические дискриминантные функции или сами дискриминантные переменные. Для классификации с помощью дискриминантных переменных коэффициенты классифицирующей функции вычисляем по формуле (22). Результаты вычислений приведены в табл. 13. Значения классифицирующей функции для каждого больного вычислены по формуле (21), результаты классификации в виде классификационной матрицы представлены в табл. 14. Так как процент правильной классификации составляет 100 %, то таблицу классифицирующих функций для отдельных пациентов можно не представлять. Таблица 13 Коэффициенты классифицирующих функций
Таблица 14 Классификационная матрица
Результаты классификации с помощью расстояния Махаланобиса (формулы (25), (26)) и апостериорной вероятности принадлежности к группе в предположении нормальности распределения (формула 19) приведены в табл. 15. Таблица 15 Сводка результатов классификации
ТРЕБОВАНИЯ К ОТЧЕТУ Отчет должен содержать следующие разделы: Название и цель работы; Номер варианта задания и исходные данные; Контрольные вопросы и краткие ответы на них; Расчетные формулы, описание алгоритмов и реализующих их программ; Результаты расчетов и их анализ; Выводы. КОНТРОЛЬНЫЕ ВОПРОСЫ Какое максимальное число канонических дискриминантных функций допустимо в дискриминантном анализе? Какую информацию дают стандартизованные и структурные коэффициенты дискриминантной функции? Для данных примера 1 проведите процедуру отбора переменных с помощью стандартизованных и структурных коэффициентов. Какова интерпретация канонического коэффициента корреляции?. В каком случае учет априорных вероятностей может сильно изменить результаты классификации? ЛАБОРАТОРНАЯ РАБОТА №8 . Предсказательная аналитика с помощью нейронной сети Цель: изучить методику предсказательной аналитики Задание на выполнение работы. Ознакомиться с возможностями аналитического пакета Deductor, выполнив приведенные ниже задания. В конце работы сохранить проект. Прогнозирование с помощью нейронной сети Особенностью процесса оценки стоимости объекта имущества является его рыночный характер. Это означает, что процесс оценки объекта не ограничивается учетом одних только затрат на создание или приобретение оцениваемого объекта собственности - необходим учет совокупности ры- ночных факторов, экономических особенностей оцениваемого объекта, а также макроэкономического и микроэкономического окружения. Кроме того, рынок недвижимости очень динамичный, поэтому требуется периодическая переоценка объектов собственности. Нейросети как универсальные аппроксиматоры позволяют строить сложные нелинейные регрессионные модели типа "черный ящик". Создание моделей для оценки стоимости недвижимости могут существенно повысить эффективность работы организаций, занимающихся риэлтерской деятельностью. Рассмотрим данный механизм на примере таблицы продаж из файла «Недвижимость.txt». При импорте обратите внимание на типы и виды числовых данных (при необходимости их нужно изменить). Для построения модели использовались данные по стоимости квартир на вторичном рынке жилья одного из крупных городов России (2011 год). Каждая квартира характеризуется следующими свойствами: • Количество комнат (1-3); • Признак этажности (первый/последний или нет); • Площадь общая, м2; • Площадь жилая, м2; • Площадь кухни, м2; • Наличие агентства – продается объект напрямую или через агентство; • Состояние квартиры – экспертная оценка по шкале от 2 до 5 (2 – нуждается в ремонте, 5 – отличное состояние квартиры); • Тип планировки; • Район – географическая принадлежность; Результирующий признак – стоимость квартиры в тыс. рублей. Предварительно проведем аудит выборки при помощи узла «Качество данных». Все настройки мастера обработки этого узла оставим предлагаемыми по умолчанию. В результате откроется визуализатор «Оценка качества данных». Аудит данных обнаружил несколько выбросов (выходящих за границы 3-сигма) и экстремальных значений (выходящих за границы 5-сигма). В частности, детализация показывает, что для поля «Общая площадь» есть три экстремальных значения 133 и 134 м2 (рис. 8.1). Вообще, нейросетевые модели достаточно устойчивы к шумам и вы- бросам, тем не менее, экстремальные значения лучше все-таки удалить. По умолчанию предлагается ограничить найденные выбросы и экстремальные значения. Переопределим это действие: • для выбросов выбрать пункт «Оставить без изменения»; • для экстремальных значений – «Удалять». Для того чтобы эти действия были произведены, после узла «Качество данных» добавьте узел «Редактирование выбросов». Для оценки качества нейросетевой модели можно использовать прием перекрестной проверки (cross-validation). Это повторение всего процесса обучения и тестирования несколько раз при различных случайных выборках. 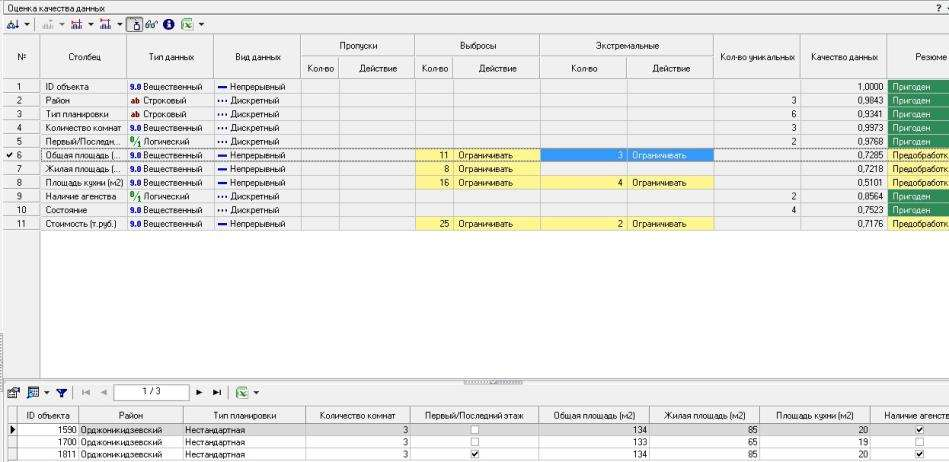 Рис. 8.1 Для определения ошибки принято делать десятиблочную перекрест- ную проверку. Данные случайным образом разделяются на 10 блоков, в каждом из которых классы наблюдений представлены приблизительно так же, как и в исходном множестве. Затем модель обучается на 9/10 данных и тестируется на оставшейся 1/10 части. Полученные 10 значений ошибки усредняются, и результат рассматривается как общая ошибка модели. Для того, чтобы заложить эту логику в сценарий необходимо разде- лить выборку на 10 примерно равных частей. Это делается при помощи не- скольких узлов. а) Узел «Квантование» выделяет 10 квантилей, в каждом от 212 до 213 записей (рис. 8.2). 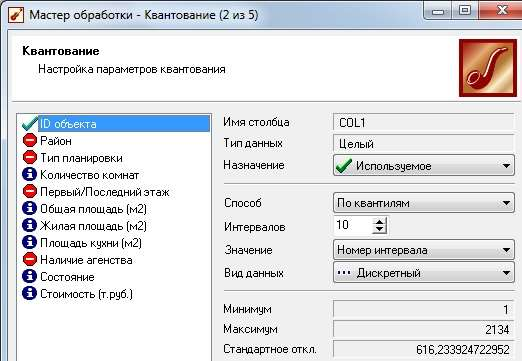 Рис. 8.2 б) Узел «Группировка» производит группировку по полю «ID объек- та» (рис. 8.3). 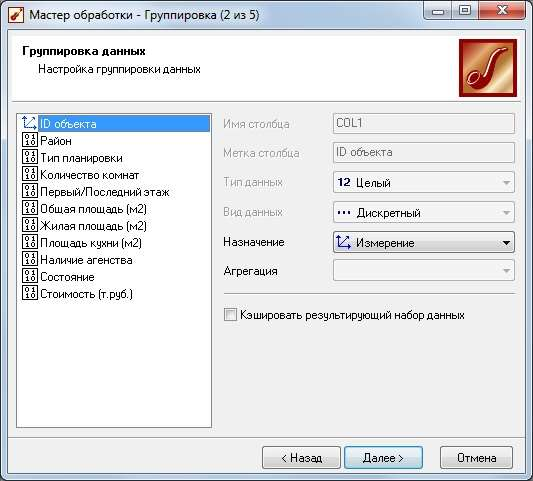 Рис. 8.3 в) Узел «Настройка набора данных» формируют список уникальных номеров блоков с меткой № блока и именем Block (рис. 8.4). 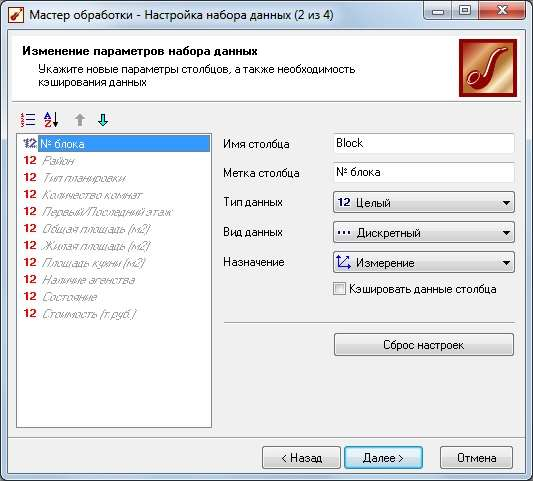 Рис. 8.4 г) Узел «Слияние с узлом» (полное внешнее соединение) «размножает» записи исходной выборки (узел «Квантование») в число раз, равное количеству блоков – в итоге имеем 21280 записей и идентификатор группы для каждой из них. Проведем построение нейросети для нулевого блока. Для этого необ- ходимо использовать фильтр. Выделите тестовое и обучающее множество при помощи «Калькуля- тора», записав в него логическое выражение (рис. 8.5). 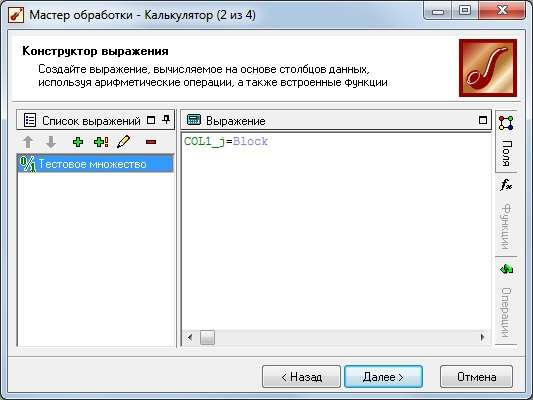 Рис. 8.5 Теперь все готово к построению модели нейросети. Запустите мастер обработки и выберите обработчик «Нейросеть» (рис. 8.6). 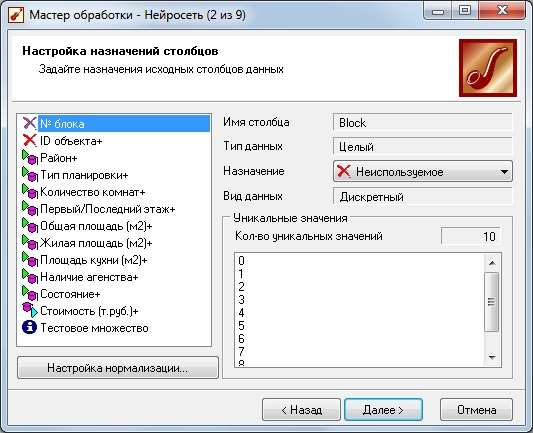 Рис. 8.6 Для полей, содержащих информацию о состоянии, комнатах, этажах и агентстве назначить нормализатор «Уникальные значения». На 3 шаге указать способ разделения – «по столбцу» и столбец «Те- стовое множество». На 4 шаге настраивается структура нейронной сети. Укажите количе- ство скрытых слоев – 1, а количество нейронов – 5. На следующих шагах настройки измените только количество эпох, по достижению которых нейросеть останавливает обучение, на 1000. После чего запустите нейросеть на обучение. Для отображения полученных результатов выберите следующие визу- ализаторы: «Граф нейросети» для отображения структурной схемы по- строенной нейронной сети; «Диаграмма рассеяния» для просмотра каче- ства обучения; «Что-если» для расчета стоимости квартиры по введенным пользователям характеристикам. Рассмотрим визуализатор «Граф нейросети» (рис. 8.7). На нем гра- фически отображается нейронная сеть со всеми ее нейронами и синаптиче- скими связями. Значения весов, отображаются определенным цветом, по- смотреть которое можно по цветовой шкале, расположенной внизу окна.  Рис. 8.7 Диаграмма рассеяния показывает качество регрессионной модели. Большая масса точек сосредоточена вблизи линии идеальных значений, по- этому можно сказать, что модель обучилась хорошо (рис. 8.8). 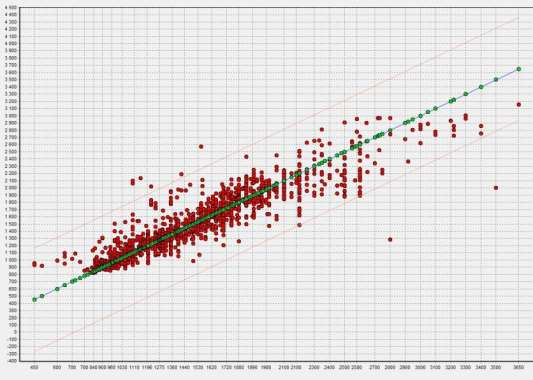 Рис. 8.8 Построение нейросетевой модели для одного блока окончено. Рассчитаем среднюю ошибку аппроксимации для стоимости недвижи- мости при помощи калькулятора. Это позволит более точно численно оце- нить качество модели. Для этого используем «Калькулятор» (рис. 8.9). Для расчета количества записей в область Выражение ввести 1. 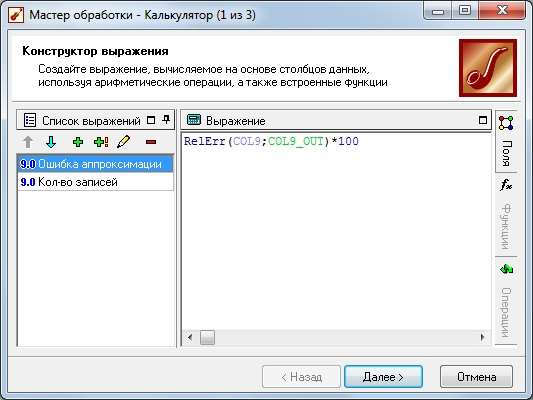 Рис. 8.9 Сгруппируйте данные как показано на рис. 8.10. 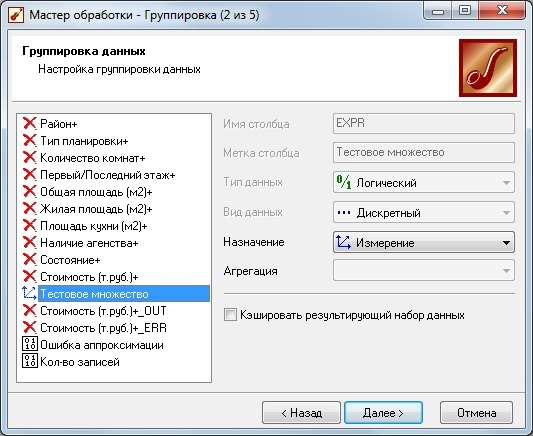 Рис. 8.10 Используя «Калькулятор», добавим новое поле «Средняя ошибка ап- проксимации», рассчитываемое как отношение ошибки и количества запи- сей. Ошибка получилась в районе 8,0%. Хорошим результатом считается ошибка до 10-12%. Модель является применимой для расчета стоимости недвижимости. Для проведения 10-блочной кросс-валидации требуется проделать по- следовательность действий как в предыдущем шаге, но для всех блоков. Это делается при помощи «Групповой обработки» от узла «Внешнее соеди- нение». На первом шаге мастера обработки этого узла укажем поле «№ блока» как поле, по которому будет проводиться групповая обработка. На следу- ющих двух шагах нужно указать цепочку узлов для групповой обработки. Это будет ветвь от узла фильтра блока до расчета средней ошибки аппрок- симации. В параметрах групповой обработки поставить первый, третий и чет- вертый флажок. Запуск групповой обработки всегда приведет к построению 10 моде- лей нейросетей. В итоге мы получим 10 оценок средней ошибки аппрокси- мации на обучающем и на тестовом множествах. Из рис. 8.11 видно, что минимальная ошибка достигается на подвы- борке под номером 6. Выберем эту модель как основную и перенастроим ветвь с фильтром на этот номер блока. 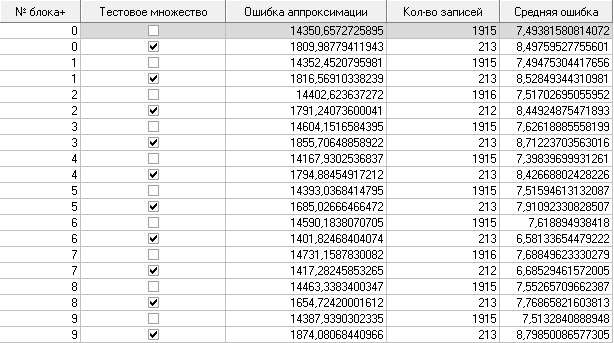 Рис. 8.11 На основе лучшей модели, построенной на подвыборке № 7, спрогно- зируем стоимость следующего объекта недвижимости: • количество комнат – 3; • район – Орджоникидзевский; • планировка – Свердловский вариант; • этаж – последний; • площадь – 63; • жилая площадь – 41; • кухня – 8; • состояние – 4; • наличие агентства - нет. Для этого воспользуемся визуализатором Что-Если (рис. 8.12). 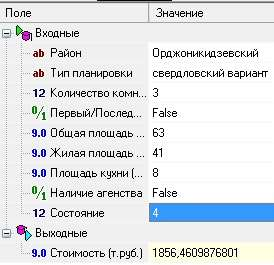 Рис. 8.12 По прогнозу нейронной сети стоимость квартиры составляет 1856,5 тыс. рублей. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
