Ауе. Основное 4 МУ АД Лаб 4 сем (1). Методические указания к проведению лабораторных занятий по нормативной учебной дисциплине естественнонаучного цикла Анализ данных
 Скачать 6.5 Mb.
|
|
Задание для самостоятельного выполнения 1. Используя результаты файл «dynamics_website.txt» построить скользящее окно с глубиной погружения № варианта +2. 2. Построить и оценить диаграмму рассеяния. 3. Осуществить прогнозирование на 6 периодов. 4. Визуализировать данные в виде гистограммы. 5. Сделать выводы по результатам анализа. Лабораторная работа № 7 Дискриминантный анализ Цель работы: изучение основных процедур дискриминантного анализа: дискриминации и классификации, построение и определение количества дискриминантных функций и их разделительной способности, нахождение классифицирующих функций с использованием функций Фишера и расстояния Махаланобиса. ВВЕДЕНИЕ Дискриминантный анализ является разделом многомерного статистического анализа, который позволяет изучать различия между двумя и более группами объектов по нескольким переменным одновременно. Дискриминантный анализ – это общий термин, относящийся к нескольким тесно связанным статистическим процедурам. Эти процедуры можно разделить на методы интерпретации межгрупповых различий – дискриминации и методы классификации наблюдений по группам [5]. Методы классификации связаны с получением одной или нескольких функций, обеспечивающих возможность отнесения данного объекта к одной из групп. Эти функции называются классифицирующими. Задачи дискриминантного анализа можно разделить на три типа. Задачи первого типа часто встречаются в медицинской практике. Допустим, что мы располагаем информацией о некотором числе индивидуумов, болезнь каждого из которых относится к одному из двух или более диагнозов. На основе этой информации нужно найти функцию, позволяющую поставить в соответствие новым индивидуумам характерные для них диагнозы. Второй тип задачи относится к ситуации, когда признаки принадлежности объекта к той или иной группе потеряны, и их нужно восстановить. Примером может служить определение пола давно умершего человека по его останкам, найденным при археологических раскопках. Задачи третьего типа связаны с предсказанием будущих событий на основании имеющихся данных. Такие задачи возникают при прогнозе отдаленных результатов лечения, например, прогноз выживаемости оперированных больных. ЗАДАНИЕ Получить у преподавателя варианты матрицы исходных данных, степенью точности. Составить программу и оценить следующие характеристики: среднее значение переменных внутри классов, общее среднее; матрицу перекрестных произведений и ковариационную матрицу общего рассеяния; матрицу внутригрупповых квадратов и перекрестных произведений и корреляционную матрицу; матрицу межгрупповых квадратов и перекрестных произведений и корреляционную матрицу; коэффициенты канонической дискриминантной функции; коэффициенты классифицирующей функции Фишера; используя оценки априорных вероятностей принадлежности объектов к группам, определить расстояние Махаланобиса; вычислить обобщенное расстояние Рао и его значимость. Сравнить полученные в среде MathCad результаты с оценками, найденными с помощью ППП STATISTICA или STATGRAPHICS. Дать ответ на контрольные вопросы. Оформить отчет. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ 1. ДИСКРИМИНАЦИЯ Основной целью дискриминации является нахождение такой линейной комбинации переменных (в дальнейшем эти переменные будем называть дискриминантными переменными), которая бы оптимально разделила рассматриваемые группы. Линейная функция  (1)называется канонической дискриминантной функцией с неизвестными коэффициентами  . Здесь  значение дискриминантной функции для m-го объекта в группе k;  значение дискриминантной переменной  для m-го объекта в группе k. С геометрической точки зрения дискриминантные функции определяют гиперповерхности в p-мерном пространстве. В частном случае при p = 2 она является прямой, а при p = 3 – плоскостью. Коэффициенты первой канонической дискриминантной функции выбираются таким образом, чтобы центроиды различных групп как можно больше отличались друг от друга. Коэффициенты второй группы выбираются также, но при этом налагается дополнительное условие, чтобы значения второй функции были некоррелированы со значениями первой. Аналогично определяются и другие функции. Отсюда следует, что любая каноническая дискриминантная функция  имеет нулевую внутригрупповую корреляцию с  . Если число групп равно g, то число канонических дискриминантных функций будет на единицу меньше числа групп. Однако по многим причинам практического характера полезно иметь одну, две или же три дискриминантных функций. Тогда графическое изображениее объектов будет представлено в одно-, двух- и трехмерных пространствах. Такое представление особенно полезно в случае, когда число дискриминантных переменных p велико по сравнению с числом групп g.Коэффициенты канонической дискриминантной функции Для получения коэффициентов  канонической дискриминантной функции нужен статистический критерий различения групп. Очевидно, что классификация переменных будет осуществляться тем лучше, чем меньше рассеяние точек относительно центроида внутри группы и чем больше расстояние между центроидами групп. Разумеется, что большая внутригрупповая вариация нежелательна, так как в этом случае любое заданное расстояние между двумя средними тем менее значимо в статистическом смысле, чем больше вариация распределений, соответствующих этим средним. Один из методов поиска наилучшей дискриминации данных заключается в нахождении такой канонической дискриминантной функции d, которая бы максимизировала отношение межгрупповой вариации к внутригрупповой [1, 2, 3, 4]  (2)где B – межгрупповая и W – внутригрупповая матрицы рассеяния наблюдаемых переменных от средних. В некоторых работах [3, 4] в (2) вместо W используют матрицу рассеяния T объединенных данных. Рассмотрим максимизацию отношения (2) для произвольного числа классов. Введем следующие обозначения: g – число классов; р – число дискриминантных переменных;  число наблюдений в k-й группе; общее число наблюдений по всем группам; величина переменной i для m-го наблюдения в k-й группе; средняя величина переменной i в k-й группе; среднее значение переменной i по всем группам; общая сумма перекрестных произведений для переменных u иv; внутригрупповая сумма перекрестных произведений для переменных u и v; ;  .В модели дискриминации должны соблюдаться следующие условия: число групп:  ;число объектов в каждой группе:  ;число дискриминантных переменных:  ;дискриминантные переменные измеряются в интервальной шкале; дискриминантные переменные линейно независимы; ковариационные матрицы групп примерно равны; дискриминантные переменные в каждой группе подчиняются многомерному нормальному закону распределения. Рассмотрим задачу максимизации отношения (2) когда имеются g групп. Оценим сначала информацию, характеризующую степень различия между объектами по всему пространству точек, определяемому переменными групп. Для этого вычислим матрицу рассеяния T, которая равна сумме квадратов отклонений и попарных произведений наблюдений от общих средних  по каждой переменной. Элементы матрицы T определяются выражением [3, 4] , (3)где  ; .Запишем это выражение в матричной форме. Обозначим p-мерную случайную векторную переменную k-й группы следующим образом  .Тогда объединенная p-мерная случайная векторная переменная всех групп будет иметь вид  .Общее среднее этой p-мерной случайной векторной переменной будет равен вектору средних отдельных признаков  .Матрица рассеяния от среднего при этом запишется в виде  . (4)Если использовать векторную переменную объединенных переменных X, то матрица T определится по формуле  .Матрица T содержит полную информацию о распределении точек по пространству переменных. Диагональные элементы представляют собой сумму квадратов отклонений от общего среднего и показывают как ведут себя наблюдения по отдельно взятой переменной. Внедиагональные элементы равны сумме произведений отклонений по одной переменной на отклонения по другой. Если разделить матрицу T на  , то получим ковариационную матрицу. Для проверки условия линейной независимости переменных полезно рассмотреть вместо T нормированную корреляционную матрицу.Для измерения степени разброса объектов внутри групп рассмотрим матрицу W, которая отличается от T только тем, что ее элементы определяются векторами средних для отдельных групп, а не вектором средних для общих данных. Элементы внутригруппового рассеяния определятся выражением  . (5)Запишем это выражение в матричной форме. Данным g групп будут соответствовать векторы средних 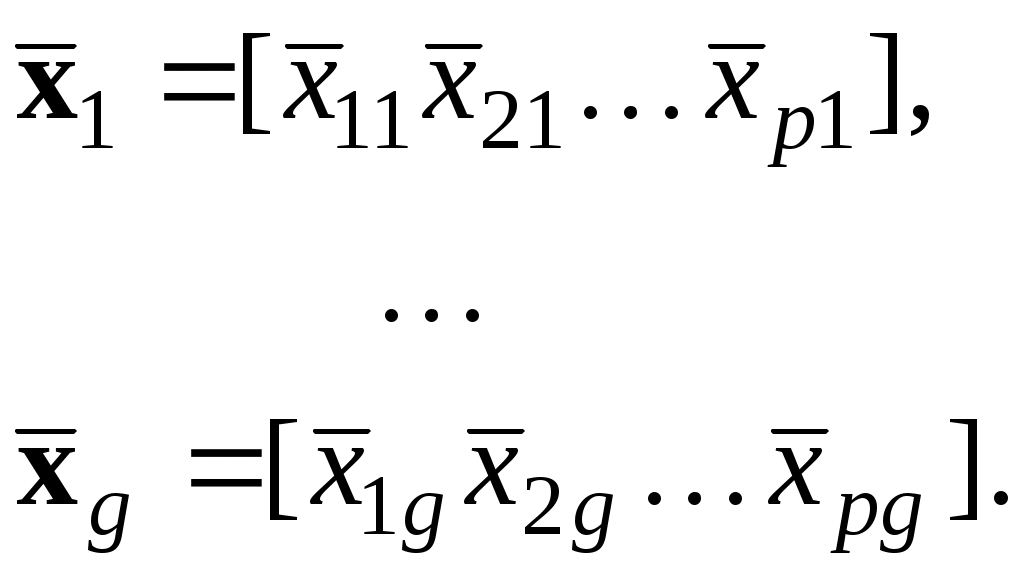 (6)Тогда матрица внутригрупповых вариаций запишется в виде  . (7)Если разделить каждый элемент матрицы W на (n - g), то получим оценку ковариационной матрицы внутригрупповых данных. Когда центроиды различных групп совпадают, то элементы матриц T и W будут равны. Если же центроиды групп различные, то разница  (8)будет определять межгрупповую сумму квадратов отклонений и попарных произведений. Если расположение групп в пространстве различается (т.е. их центроиды не совпадают), то степень разброса наблюдений внутри групп будет меньше межгруппового разброса. Отметим, что элементы матрицы В можно вычислить и по данным средних  . (9)Матрицы W и B содержат всю основную информацию о зависимости внутри групп и между группами. Для лучшего разделения наблюдений на группы нужно подобрать коэффициенты дискриминантной функции из условия максимизации отношения межгрупповой матрицы рассеяния к внутригрупповой матрице рассеяния при условии ортогональности дискриминантных плоскостей. Тогда нахождение коэффициентов дискриминантных функций сводится к решению задачи о собственных значениях и векторах [3]. Это утверждение можно сформулировать так: если спроектировать g групп р-мерных выборок на (g - 1) пространство, порожденное собственными векторами  , то отношение (2) будет максимальным, т. е. рассеивание между группами будет максимальным при заданном внутригрупповом рассеивании. Если бы мы захотели спроектировать g выборок на прямую при условии максимизации наибольшего рассеивания между группами, то следовало бы использовать собственный вектор  ), соответствующий максимальному собственному числу  . При этом дискриминантные функции можно получать: по нестандартизованным и стандартизованным коэффициентам.Нестандартизованные коэффициенты. Пусть  и  соответственно собственные значения и векторы. Тогда условие (2) в терминах собственных чисел и векторов запишется в виде ,что влечет равенство  , или в матричной записи , (10)где δij – символ Кронекера. Таким образом, решение уравнения  позволяет нам определить компоненты собственных векторов, соответствующих дискриминантным функциям. Если B и W невырожденные матрицы, то собственные корни уравнения такие же, как и у  . Решение системы уравнений (10) можно получить путем использования разложения Холецкого  матрицы  и решения задачи о собственных значениях .Каждое решение, которое имеет свое собственное значение  и собственный вектор  , соответствует одной дискриминантной функции. Компоненты собственного вектора можно использовать в качестве коэффициентов дискриминантной функции. Однако при таком подходе начало координат не будет совпадать с главным центроидом. Для того, чтобы начало координат совпало с главным центроидом нужно нормировать компоненты собственного вектора [4] . (11)Нормированные коэффициенты (11) получены по нестандартизованным исходным данным, поэтому они называются нестандартизованными. Нормированные коэффициенты приводят к таким дискриминантным значениям, единицей измерения которых является стандартное квадратичное отклонение. При таком подходе каждая ось в преобразованном пространстве сжимается или растягивается таким образом, что соответствующее дискриминантное значение для данного объекта представляет собой число стандартных отклонений точки от главного центроида. Стандартизованные коэффициенты можно получить двумя способами: 1) по формуле (11), если исходные данные были приведены к стандартной форме; 2) преобразованием нестандартизованных коэффициентов к стандартизованной форме:  , (12)где  сумма внутригрупповых квадратов i-й переменной, определяемой по формуле (5). Стандартизованные коэффициенты полезно применять для уменьшения размерности исходного признакового пространства переменных. Если абсолютная величина коэффициента для данной переменной для всех дискриминантных функций мала, то эту переменную можно исключить, тем самым сократив число переменных. Структурные коэффициенты определяются коэффициентами взаимной корреляции между отдельными переменными и дискриминантной функцией. Если относительно некоторой переменной абсолютная величина коэффициента велика, то вся информация о дискриминантной функции заключена в этой переменной. Структурные коэффициенты полезны при классификации групп. Структурный коэффициент можно вычислить и для переменной в пределах отдельно взятой группы. Тогда получаем внутригрупповой структурный коэффициент, который вычисляется по формуле , (13)где  внутригрупповой структурный коэффициент для i-й переменной и j-й функции;  внутригрупповые структурные коэффициенты корреля-ции между переменными iи k;  стандартизованные коэффициенты канонической функции для переменной k и функции j.Структурные коэффициенты по своей информативности несколько отличаются от стандартизованных коэффициентов. Стандартизованные коэффициенты показывают вклад переменных в значение дискриминантной функции. Если две переменные сильно коррелированы, то их стандартизованные коэффициенты могут быть меньше по сравнению с теми случаями, когда используется только одна из этих переменных. Такое распределение величины стандартизованного коэффициента объясняется тем, что при их вычислении учитывается влияние всех переменных. Структурные же коэффициенты являются парными корреляциями и на них не влияют взаимные зависимости прочих переменных. 1.2. Число дискриминантных функций Общее число дискриминантных функций не превышает числа дискриминантных переменных и, по крайней мере, на единицу меньше числа групп. Степень разделения выборочных групп зависит от величины собственных чисел: чем больше собственное число, тем сильнее разделение. Наибольшей разделительной способностью обладает первая дискриминантная функция, соответствующая наибольшему собственному числу  , вторая обеспечивает максимальное различение после первой и т. д. Различительную способность i-й функции оценивают по относительной величине в процентах собственного числа  от суммы всех  .Коэффициент канонической корреляции. Другой характеристикой, позволяющей оценить полезность дискриминантной функции является коэффициент канонической корреляции  . Каноническая корреляция является мерой связи между двумя множествами переменных. Максимальная величина этого коэффициента равна 1. Будем считать, что группы составляют одно множество, а другое множество образуют дискриминантные переменные. Коэффициент канонической корреляции для i-й дискриминантной функции определяется формулой: . (14)Чем больше величина , тем лучше разделительная способность дискриминантной функции. Остаточная дискриминация. Так как дискриминантные функции находятся по выборочным данным, они нуждаются в проверке статистической значимости. Дискриминантные функции представляются аналогично главным компонентам. Поэтому для проверки этой значимости можно воспользоваться критерием, аналогичным дисперсионному критерию в методе главных компонент. Этот критерий оценивает остаточную дискриминантную способность, под которой понимается способность различать группы, если при этом исключить информацию, полученную с помощью ранее вычисленных функций. Если остаточная дискриминация мала, то не имеет смысла дальнейшее вычисление очередной дискриминантной функции. Полученная статистика носит название «  » и вычисляется по формуле: , (15)где k – число вычисленных функций. Чем меньше эта статистика, тем значимее соответствующая дискриминантная функция. Величина  (16)имеет хи-квадрат распределение с  степенями свободы. Вычисления проводим в следующем порядке. Находим значение критерия  при k = 0. Значимость критерия подтверждает существование различий между группами. Кроме того, это доказывает, что первая дискриминантная функция значима и имеет смысл ее вычислять.Определяем первую дискриминантную функцию, и проверяем значимость критерия при k = 1. Если критерий значим, то вычисляем вторую дискриминантную функцию и продолжаем процесс до тех пор, пока не будет исчерпана вся значимая информация. |