Введение_в_математический_анализ. Методические указания к самостоятельной работе по дисципли не б. 1 Математика

• Название: Методические указания к самостоятельной работе по дисципли не б. 1 Математика
• Дата: 27.05.2022
• Размер: 168.01 Kb.
• Имя файла: Введение_в_математический_анализ.docx
• Тип: Методические указания; #552190
• страница: 22 из 27

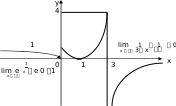
Пример 4.

f(x) _ (x1) ² ,

при

0  x  3 ;

_ 1

^ 3  x

, при

x 3 .

Решение. Функция f(x)определена на всей числовой оси.

Каждая из функций

1


e^x,

(x1)²

_и 1

3 x

в своей области опреде-

ления непрерывны, следовательно, функция f(x)может иметь разрыв только в точках x₁=0 и x₂=3. Найдем односторонние пределы функции f(x)в этих точках:

1 1

 ¹

lim

x00

lim

x00

f(x) lim

x00

f(x) lim

x00

e^x e^0  e

(x1)² 1 .

 _e  0,

Пределы конечны и различны => в точке x₁= 0 разрыв 1-

го рода. Так как

lim

x00

f(x)1

и по условию

f(0 )1, делаем за-

ключение, что функция y=f(x) непрерывна в точке x=0 справа.

lim

x30

f(x) lim ( x1) ²  4,

x30

lim

f(x) lim

1 _ 1

  .

x30

x30 _{3 x 0}

Один из пределов оказался равен –∞ => функция f(x)

имеет в точке x₂ = 3 разрыв 2-го рода.

График функции f(x)получим, если для x(,0) по-

1

строим график функции


y e^x, на промежутке [0,3] это будет

соответствующая часть параболы y (x1) ² , для x(3,) –

соответствующая ветвь гиперболы

y ¹ (рис. 5.13).

3 x

Рис. 5.13