Введение_в_математический_анализ. Методические указания к самостоятельной работе по дисципли не б. 1 Математика

• Название: Методические указания к самостоятельной работе по дисципли не б. 1 Математика
• Дата: 27.05.2022
• Размер: 168.01 Kb.
• Имя файла: Введение_в_математический_анализ.docx
• Тип: Методические указания; #552190
• страница: 20 из 27

Примеры на нахождение точек разрыва функции и их классификацию

Пример 1. Изобразить схематично график функции

y= f(x), удовлетворяющей условиям:

lim

x 10

lim

x 20

f(x) 2 ,

f(x) 3,

lim

x 10

lim

x 20

f(x) 1,

f(x);

f(1) 1;

lim

x 

f(x)  ,

lim

x 

f(x) 0;

f(0)=0.
График функции изображен на рис. 5.8.

x

Рис. 5.8

x= –1 – точка разрыва 1-го рода.

Так как

x= –1 справа.

lim

x 10

f(x) f(1),

то функция непрерывна в точке

В точке x= 2 разрыв 2-го рода.

В примерах 2–8 требуется найти точки разрыва функции, установить их характер и изобразить схематично график функции в окрестности точек разрыва (а если удастся, и во всей области определения).

Пример 2.

f(x)

x _.

x² 9

Решение. Функция определена и, следовательно, не- прерывна на всей числовой оси за исключением точек x₁ = –3 и x₂ = 3. В этих точках функция терпит разрыв. Найдем одно- сторонние пределы функции в этих точках.

lim

^x  ^3 _{  .}

₂  

x30 _x

9 _  0 _

Поясним полученный результат. Знаменатель функции

f(x)

x


x² 9

при x→ –3–0 будет стремиться к нулю, но так как

при этом левее точки x = –3 величина x² будет все время оста- ваться больше числа 9, то разность (x²– 9) будет стремиться к нулю, оставаясь все время положительной. Здесь и далее +0 обозначение бесконечно малой величины, которая стремится к нулю, оставаясь положительной; –0 – обозначение бесконечно малой величины, которая стремится к нулю, оставаясь отрица- тельной.

Закончим нахождение односторонних пределов:

lim

^x  ^{ 3}  _{   ;}

 

x  3  0 _x² <sub> 9

</sub>  0 _

lim

^x  <sup>3

</sup>    ;

lim

^x  <sup>3

</sup>    .

x 30 _x² _{ 9}

 _{ 0} 

x 30 _x² _{ 9}

 _{ 0} 








Все односторонние пределы оказались равны ∞ => x₁= – 3, x₂=3 – точки разрыва второго рода. Изобразим поведение функ- ции в окрестности точек разрыва на основании проведенного исследования (рис. 5.9).

В данном случае легко построить график функции полно- стью, если найти

^x  ^  ^{1 0}

lim

 ^{ lim x }



 0.

x   _x² _{9   }

x   _1⁹ ₁


2
x

Полученный результат означает, что при x → ± ∞график функции будет прижиматься к оси Ox.

Кроме этого, используя то, что данная функция нечетная и при этом f(0) = 0, можно построить график функции на всей области определения (рис.5.10).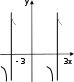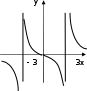





Рис. 5.9 Рис. 5.10


 
1