Введение_в_математический_анализ. Методические указания к самостоятельной работе по дисципли не б. 1 Математика
 Скачать 168.01 Kb. Скачать 168.01 Kb.
|
КЛАССИФИКАЦИЯ ТОЧЕК РАЗРЫВА ФУНКЦИИВ чём заключается необходимое и достаточное условие непрерывности функции в точке x0 ?Функция y=f(x)непрерывна в точке x0 тогда и только то- гда, когда lim xx0 0 f(x) lim xx0 0 f(x) lim x x0 f(x) f(x0 ). Если это условие каким-то образом нарушено, точку x0 на- зывают точкой разрыва функции y=f(x). Заметим, что если функция y = f(x) определена в некото- рой окрестности точки x0, но при этом не определена в самой точке x0 , точка x0 является точкой разрыва функции. Как осуществляется классификация точек разрыва функции?Определение. Точка x0 называется точкойразрыва1-горо-дафункции y = f(x) , если в этой точке существуют и конечны оба односторонних предела функции, но при этом хотя бы один из них отличен от значения f(x0). Точки разрыва 1-го рода изображены на рис. 5.1–5.4. 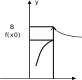 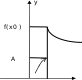 lim x x0 0 x0 x f(x) f(x0 ); lim x x0 0 x0 f(x) x A f(x0 ); lim x x0 0 f(x) B f(x0 ). lim x x0 0 f(x) f(x0 ). Рис. 5.1 Рис. 5.2 Функция, изображенная на рис. 5.1, называется непрерыв-ной слева, на рис. 5.2 – непрерывной справа. Точка разрыва, изо- браженная на рис. 5.4, называется точкой устранимого разрыва. Разрыв устраняется, если изменить значение функции в точке x0, приняв f(x0)=A. 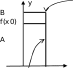 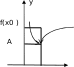 lim x x0 0 lim x x0 0 f(x) A f(x) B x0 x f(x0 ); f(x0 ). lim x x0 0 x0 f(x) x lim x x0 0 f(x) f(x0 ). Рис. 5.3 Рис. 5.4 Определение. Точка x0 называется точкой разрыва 2-городафункции y = f(x) , если хотя бы один из односторонних пределов функции в этой точке равен ∞ (рис. 5.5–5.7) или вооб- ще не существует. 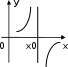 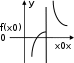 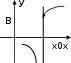 lim x x0 0 f(x); lim x x0 0 f(x) f(x0 ); lim x x0 0 f(x); lim x x0 0 f(x) . lim x x0 0 f(x) . lim x x0 0 f(x) B. Рис. 5.5 Рис. 5.6 Рис. 5.7 |
