Курс_Модел2_2 (1). Методические указания к выполнению курсовой работы дисциплины моделирование технологических процессов и основы оптимизации для студентов, обучающихся по направлению
 Скачать 3.02 Mb. Скачать 3.02 Mb.
|
|
МИНИСТЕРСТВО ВЫСШЕГО И СРЕДНЕГО СПЕЦИАЛЬНОГО ОБРАЗОВАНИЯ РЕСПУБЛИКИ УЗБЕКИСТАН ТАШКЕНТСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им ИСЛАМА КАРИМОВА К А Ф Е Д Р А АВТОМАТИЗАЦИЯ ПРОИЗВОДСТВЕННЫХ ПРОЦЕССОВ МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КУРСОВОЙ РАБОТЫ ДИСЦИПЛИНЫ «МОДЕЛИРОВАНИЕ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ И ОСНОВЫ ОПТИМИЗАЦИИ» для студентов, обучающихся по направлению «5311000 – АВТОМАТИЗАЦИЯ И УПРАВЛЕНИЕ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ И ПРОИЗВОДСТВ (ПО ОТРАСЛЯМ)» Ташкент 2021 МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КУРСОВОЙ РАБОТЫ ДИСЦИПЛИНЫ «МОДЕЛИРОВАНИЕ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ И ОСНОВЫ ОПТИМИЗАЦИИ» для студентов, обучающихся по направлению «5311000 - АВТОМАТИЗАЦИЯ И УПРАВЛЕНИЕ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ И ПРОИЗВОДСТВ (ПО ОТРАСЛЯМ)» Сост.: Мухитдинов Д.П., Шамсутдинова В.Х. Методические указания соответствуют государственному образовательному стандарту дисциплины «Моделирование технологических процессов и основы оптимизации» направления бакалаврской подготовки «5311000 – Автоматизация и управление технологическими процессами и производством». Пособие содержит краткое описание, математические модели, а также алгоритмы расчета теплообменных, массообменных и реакционных аппаратов. Представлены экспериментально-статистические методы составления математического описания. Приведены основы моделирования систем управления процессов химической технологии, используемые в рамках выполнения курсовой работы по дисциплине «Моделирование технологических процессов и основы оптимизации». Пособие предназначено для студентов третьего курса факультета электроники и автоматики, изучающих дисциплины «Моделирование технологических процессов и основы оптимизации. Подготовлено на кафедре автоматизации технологических процессов и производств Ташкентского государственного технического университета. Печатается по решению научно-методического совета Ташкентского государственного технического университета. Рецензент: Адилов Ф.Т. – д.т.н., проф. Зарипов О.О. – доц., проф. ©Ташкентский государственный технический университет СОДЕРЖАНИЕ
ВВЕДЕНИЕ Современное нефтехимическое производство – это комплекс химико-технологических стадий, информационных систем управления и коммуникаций, планово-экономических и маркетинговых служб, научно-технологических и проектных центров. Все более возрастающее значение в процессе функционирования нефтехимического комплекса приобретают информационные системы управления и передачи данных, что объясняется интенсивным развитием цифровой техники и способов обработки информации. В этой связи весьма целесообразно применение методов математического моделировании в решении задач анализа и синтеза химико-технологических процессов, а также в задачах построения систем управления данными процессами. Математическое моделирование является эффективным инструментом определения оптимальных управляющих параметров, особенно в случае процессов, физические и химические закономерности которых достаточно изучены. При этом определение управляющих параметров может осуществляться путем расчета математической модели объекта в широком диапазоне внешних возмущений. Среди методов разработки математических моделей следует выделить: – аналитические, в основе которых используются фундаментальные законы сохранения субстанции; – экспериментальные и экспериментально-аналитические, как правило, предполагающие проведение статистической обработки экспериментальных данных о состоянии входа и выхода исследуемого объекта. Владение навыками составления математического описания, а также знание моделей ХТП могут быть весьма эффективными и полезными прежде всего для операторов, инженеров и специалистов в области управления и автоматизации технологических процессов. I. МОДЕЛИРОВАНИЕ СИСТЕМЫ УПРАВЛЕНИЯ ТЕПЛООБМЕННЫМ ПРОЦЕССОМ План выполнения курсовой работы: 1. Изучение теплообменного процесса: – основные определения и закономерности; – математическая модель; – расчет коэффициентов теплоотдачи, теплопередачи; – алгоритм расчета динамики процесса. 2. Постановка задачи моделирования в соответствии с заданием на курсовую работу. 3. Получение уравнений динамики процесса. 4. Разработка моделирующей программы: – алгоритм расчета динамического режима работы теплообменника; – код моделирующей программы. 5. Анализ и представление результатов моделирования. 6. Анализ теплообменного процесса с точки зрения задач управления. 7. Разработка презентации курсовой работы (не более 8 слайдов, в т.ч. постановка задачи, математическая модель процесса, алгоритмы расчета, результаты моделирования и др.). 9. Подготовка доклада к защите (длительность доклада не более 3-4 мин.). Рекомендуемая литература: [1 – 7]. Краткое описание процесса Перенос энергии в форме тепла, происходящий между телами, имеющими различную температуру, называется теплообменом [1]. Движущей силой любого процесса теплообмена является разность температур более нагретого и менее нагретого тел, при наличии которой тепло самопроизвольно, в соответствии со вторым законом термодинамики, переходит от более нагретого к менее нагретому телу. Различают три принципиально различных элементарных способа распространения тепла: теплопроводность, конвекцию и тепловое излучение. Теплопроводность представляет собой перенос тепла вследствие беспорядочного (теплового) движения микрочастиц, непосредственно соприкасающихся друг с другом. Конвекцией называется перенос тепла вследствие движения и перемешивания макроскопических объемов газа или жидкости. Тепловое излучение – это процесс распространения электромагнитных колебаний с различной длиной волн, обусловленный тепловым движением атомов или молекул излучающего тела. В реальных условиях тепло передается не каким-либо одним из указанных выше способов, а комбинированным путем. Например, при теплообмене между твердой стенкой и газовой средой тепло передается одновременно конвекцией, теплопроводностью и излучением. Перенос тепла от стенки к газообразной (жидкой) среде или в обратном направлении называется теплоотдачей. Еще более сложным является процесс передачи тепла от более нагретой к менее нагретой жидкости (газу) через разделяющую их поверхность или твердую стенку. Этот процесс носит название теплопередачи. В непрерывно действующих аппаратах температуры в различных точках не изменяются во времени и протекающие процессы теплообмена являются установившимися (стационарными). В периодически действующих аппаратах, где температуры меняются во времени (при нагревании или охлаждении), осуществляются неустановившиеся, или нестационарные, процессы теплообмена. В химической промышленности широко распространены тепловые процессы – нагревание и охлаждение жидкостей, конденсация паров, испарение жидкостей, которые проводятся в теплообменных аппаратах, называемых теплообменниками. Теплообменники предназначены для передачи тепла от одних веществ к другим. Вещества, участвующие в процессе передачи тепла, называются теплоносителями. Теплоносители, имеющие более высокую температуру, принято называть нагревающими агентами, а теплоносители с более низкой температурой, чем среда, от которой они воспринимают тепло, – охлаждающими агентами. В зависимости от способа передачи тепла различают две основные группы теплообменников: 1) поверхностные теплообменники, в которых перенос тепла между обменивающимися теплом веществами происходит через разделяющую их поверхность теплообмена – глухую стенку; 2) теплообменники смешения, в которых тепло передается от одной среды к другой при их непосредственном соприкосновении. Поверхностные теплообменники широко распространены и их конструкции весьма разнообразны [2]. На рис. 2.1 показан кожухотрубчатый теплообменник жесткой конструкции, который состоит из корпуса, или кожуха 1, и приваренных к нему трубных решеток 2. В трубных решетках закреплен пучок труб 3. К трубным решеткам крепятся крышки 4. В теплообменнике одна из сред I движется в межтрубном пространстве, а другая II – внутри труб (в трубном пространстве). Среды обычно направляют противотоком друг к другу. При этом нагреваемую среду направляют снизу вверх, а среду, отдающую тепло, – в противоположном направлении. Такое направление движения каждой среды совпадает с направлением, в котором стремится двигаться данная среда под влиянием изменения ее плотности при нагревании или охлаждении.  Рис. 1.1. Кожухотрубный одноходовой (а) и многоходовой (б)теплообменники Расчет теплообменника с известной поверхностью теплопередачи заключается, как правило, в определении конечных температур теплоносителей при их известных начальных значениях, а также в определении требуемых расходов нагревающего или охлаждающего агентов. Математическое описание теплообменного процесса Расчет тепловой нагрузки Согласно основному уравнению теплопередачи, тепловой поток Q (расход передаваемой теплоты, тепловая нагрузка) определяется следующим образом: Q=FK∆tср, (1.1) где F – поверхность теплопередачи (м2), К – коэффициент теплопередачи (Вт/(м2·К)), ∆tср– средний температурныйнапор (средняя движущая сила) (К). Тепловую нагрузку Q при известных значениях расхода и теплофизических свойств теплоносителей можно рассчитать следующим образом: если агрегатное состояние одного из теплоносителей не меняется, то Q=Gc(tн – tк) или Q = Gc(tк −tн), (1.2) где G – расход теплоносителя (кг/с), с – удельная теплоемкость теплоносителя (Дж/(кг·град)) при средней температуре 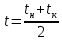 tн, tк – начальная и конечная температуры (К); 2) при конденсации насыщенных паров без охлаждения конденсата или при кипении Q=Gr (1.3) здесь r – теплота конденсации (Дж/кг); при конденсации перегретых паров с охлаждением конденсата Q=G(Iн– ctк), (1.4) где Iн – энтальпия (теплосодержание) пара (Дж/кг). Один какой-либо технологический параметр, не указанный в исходном задании (расход одного из теплоносителей или одна из температур), можно найти с помощью уравнения теплового баланса, приравнивая правые части уравнений (1.2) – (1.4) для горячего и холодного теплоносителей. В аппаратах с прямо- и противоточным движением теплоносителей средняя разность температур потоков ∆tср определяется как среднелогарифмическая между большей ∆tб и меньшей ∆tм разностями температур теплоносителей на концах аппарата: 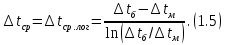 Если разности температур одинаковы или отличаются не более чем в два раза, то среднюю разность температур можно приближенно определить как среднеарифметическую: 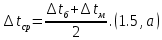 В многоходовых теплообменниках с простым смешанным током ∆tсрможно рассчитать по формуле: 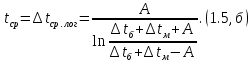 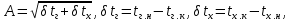 где tг.н,, tг.к. –начальнаяи конечная температура горячего теплоносителя; tх.н., хt.к. –начальная и конечная температура холодного теплоносителя; δtг, δtх – изменение температур. При изменении агрегатного состояния теплоносителя его температура постоянна вдоль всей поверхности теплопередачи и равна температуре кипения (или конденсации), зависящей от давления, состава теплоносителя. Коэффициент теплопередачи К, входящий в уравнение (1.1), можно рассчитать с помощью уравнения аддитивности термических сопротивлений на пути теплового потока: 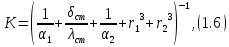 где α1, α2 – коэффициенты теплоотдачи со стороны теплоносителей; λст – теплопроводность стенки (Вт/(м·К)); δст – толщина стенки (м); 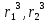 – термические сопротивления загрязнений с обеих сторон стенки ((м2·К)/Вт) [3, 4]. – термические сопротивления загрязнений с обеих сторон стенки ((м2·К)/Вт) [3, 4].Составление уравнения теплового баланса Решение задач управления, синтеза и анализа теплообменных процессов методами математического моделирования предполагает использование уравнения теплового баланса: приход тепла = расход тепла (статическая модель); накопление тепла = приход тепла – расход тепла (динамическая модель). Пусть задан расход более нагретого теплоносителя Gг, его энтальпия на входе аппарата Iг.н. и на выходе из аппарата Iг.к..Соответственно, расход более холодного теплоносителя – Gх, его начальная энтальпия Iх.н. и конечная –Iх.к.Тогда уравнение теплового баланса для установившегося (неизменного во времени) режима [1]: Q=Gг(Iг.н.–Iг.к.) = Gх(Iх.к.–Iх.н.) (1.7) Если теплообмен протекает без изменения агрегатного состояния теплоносителей, то энтальпии последних равны произведению теплоемкости с на температуру t (оС): Iг.н = cг.нtг.н, Iг.к = cг.кtг.к; Iх.н = cх.нtх.н, Iх.к = cх.кtх.к. (1.8) Величинысг.н.исг.к. представляют собой средние удельные теплоемкости более нагретого теплоносителя в пределах изменения температур от 0 до tг.н. (на входе в аппарат) и до tг.к.(на выходе из аппарата) соответственно;сх.н.исх.к. –средние удельные теплоемкости холодного теплоносителя в пределах 0 – tх.н. и 0 – tх.к. соответственно. Если теплообмен осуществляется при изменении агрегатного состояния теплоносителя (конденсация пара, испарение жидкости) или в процессе теплообмена протекают химические реакции, сопровождаемые тепловыми эффектами, то в тепловом балансе должно быть учтено тепло, выделяющееся при физическом или химическом превращении. Так, при конденсации насыщенного пара величина Iг.н. в уравнении (1.7) представляет собой энтальпию поступающего в аппарат пара, а Iг.к.–энтальпию удаляемого парового конденсата. В случае использования перегретого пара его энтальпия Iг.н.складывается из тепла, отдаваемого паром при охлаждении от температуры tг.н. до температуры насыщенияtгнас., тепла конденсации пара и тепла, выделяющегося при охлаждении конденсата: Q =Gг(Iг.н.– Iг.к.) =Gгcг.п.(tг.н. −tг.нас.)+Gгr+Gгcг.к.(tг.нас. – tг.к.), (1.9) где cг.п. и cг.к –удельные теплоемкости пара и конденсата;tг.к –температураконденсата на выходе. При обогреве насыщенным паром, если конденсат не охлаждается, т.е. tг.к = tг.н = tг.нас, первый и третий члены правой части уравнения (1.9) из теплового баланса исключаются. Для неустановившегося режима, когда наблюдается изменение температуры теплоносителя dt в интервале времени dτ, уравнения баланса для одного из теплоносителей, подаваемого в трубное пространство: dQ = Vρхcхdtх.к. = Gг(Iг.н.–Iг.к.)dτ–Gх (Iх.к.-Iх.н)dτ, где V – объем трубного пространства (м3), ρх – плотность нагреваемой среды (кг/м3). Преобразуем уравнение баланса и получим дифференциальное уравнение относительно температуры холодного теплоносителя на выходе аппарата: 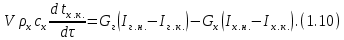 В качестве примера составим уравнение баланса для нагреваемой жидкости в трубном пространстве за малый промежуток времени dτ. В этом случае следует учесть: – теплоту, поступившую в теплообменник с жидкостью, dQ = Gхcхtх.н.dτ; – теплоту, полученную жидкостью от горячего теплоносителя через теплопередающую поверхность металлической стенки труб и затраченную на увеличение температуры жидкости tх.к.,dQ = KF∆tсрdτ; – теплоту, уходящую с жидкостью из теплообменника,dQ = Gxcxtх.к.dτ; Тогда уравнение баланса имеет вид: 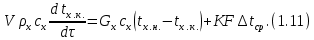 Расчет коэффициентов теплоотдачи Выбор уравнения для расчета коэффициентов теплоотдачи, используемых в уравнениях баланса, зависит от характера теплообмена (без изменения агрегатного состояния, кипение или конденсация), вида поверхности теплообмена, типа конструкции, режима движения теплоносителя [3, 4]. 1. При движениитеплоносителя в прямых трубах круглого сечения или в каналах некруглого сечения без изменения агрегатного состояния коэффициент теплоотдачи определяют по следующим уравнениям: 1.1. При развитом турбулентном движении (Re ≥104): 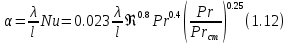 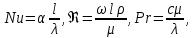 где Nu – критерий Нуссельта;Pr– критерий Прандтля; Prст– критерий Прандтля, рассчитанный при температуре стенки; ω – скорость (м/с). Определяющим размером l является эквивалентный диаметр (для труб круглого сечения – внутренний диаметр трубы dтвнутр(м)); определяющей температурой, при которой рассчитывают физические свойства среды, – средняя температура теплоносителя. Физические свойства: λ – теплопроводность; ρ – плотность; µ – динамическая вязкость (Па·с). 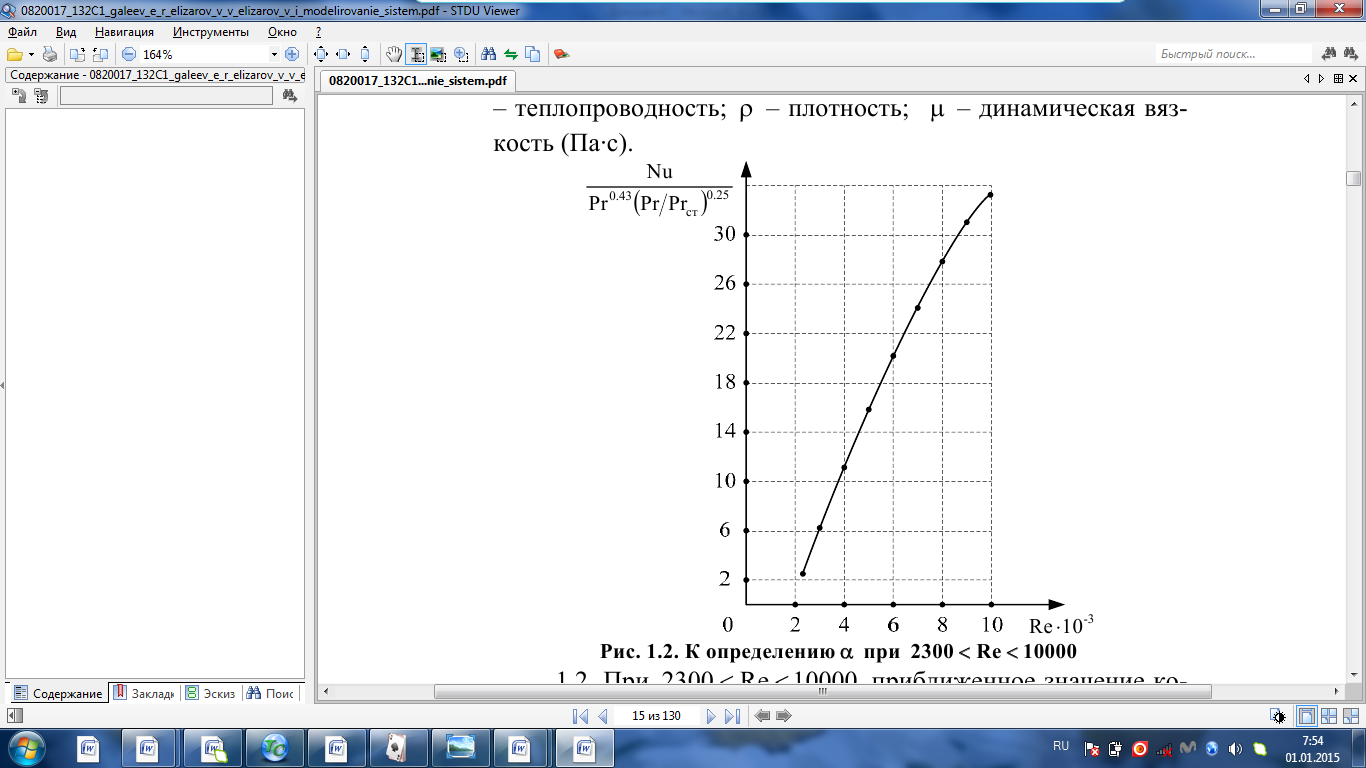 Рис. 1.2. К определению α при 2300 1.2. При 2300 1.3. В ламинарном режиме (Re ≤ 2300): а) при значениях 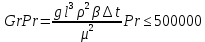 l (Gr – критерий Грасгофа, g – ускорение свободного падения (м/с2), β – коэффициент объемного расширения теплоносителя (1/град), ∆t – разность температур между стенкой и теплоносителем): l (Gr – критерий Грасгофа, g – ускорение свободного падения (м/с2), β – коэффициент объемного расширения теплоносителя (1/град), ∆t – разность температур между стенкой и теплоносителем):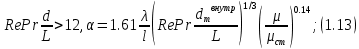 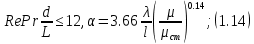 где µст – вязкость теплоносителя при температуре стенки; L – длина трубы (м); б) при значениях GrPr> 500000 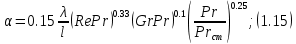 2. При движении теплоносителя в межтрубном пространстве с сегментными перегородками коэффициент теплоотдачи рассчитывают по уравнениям: 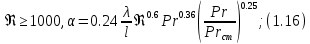 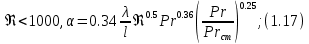 В уравнениях (1.16), (1.17) за определяющий геометрический размер принимают наружный диаметр теплообменных труб. Скорость потока определяют для площади сечения потока между перегородками [3]. 3. При конденсации пара на наружной поверхности пучка из n вертикальных труб коэффициент теплоотдачи: 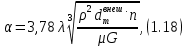 для n горизонтальных труб длиной L 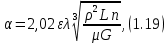 здесь dтвнеш. внешний диаметр трубы, ε = 0.7 при n ≤100 и ε= 0.6 при n > 100. |
