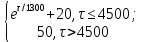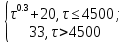Курс_Модел2_2 (1). Методические указания к выполнению курсовой работы дисциплины моделирование технологических процессов и основы оптимизации для студентов, обучающихся по направлению
 Скачать 3.02 Mb. Скачать 3.02 Mb.
|
|
Управление динамическими режимами работы теплообменного аппарата. Режимные параметры теплообменного оборудования являются переменными величинами как во времени, так и в пространстве. Такие параметры, как температуры теплоносителей в разных точках аппарата имеют различные значения. Основной причиной изменения параметров во времени является воздействия возмущений на аппарат в ходе его эксплуатации. В частности, отклонения входных параметров (расход, температура одного из теплоносителей) от проектных значений представляют собой возмущения на входе процесса. Наличие возмущений может привести к нарушению условий удовлетворительного функционирования аппарата, т.е. невыполнению требований по конечным температурам теплоносителей или их агрегатному состоянию. Для исключения таких ситуаций необходима система управления, реализованная на базе контрольно-измерительных приборов и ЭВМ. Управляющим параметром теплообменного аппарата, предназначенного для нагрева, охлаждения или конденсации одного из теплоносителей, является расход второго теплоносителя. Одним из способов определения значений управляющего параметра является расчет динамической модели процесса. Расчет модели проводится программным путем. Динамическая модель процесса состоит из дифференциальных уравнений, характеризующих изменение во времени температуры движущихся в теплообменнике сред, температуры теплопередающей стенки и др. [5]. Для решения уравнений могут использоваться численные методы. Рассмотрим работу теплообменного аппарата, предназначенного для нагревания технологического потока. Модель такого аппарата представлена дифференциальными уравнениями относительно температур tх.к. и tг.к. Соответствующие уравнения составляются аналитическими методами на основе фундаментальных законов сохранения тепла и по виду аналогичны уравнению (1.11). Расчет требуемого управления осуществляется системой управления (рис. 1.3). На основе измеренного значения Gх =Gх(τ) и первого приближения расхода Gг(τ) в начальный момент времени рассчитываются коэффициенты теплоотдачи α с учетом режима течения движущихся сред по одной из формул (1.12) – (1.19). 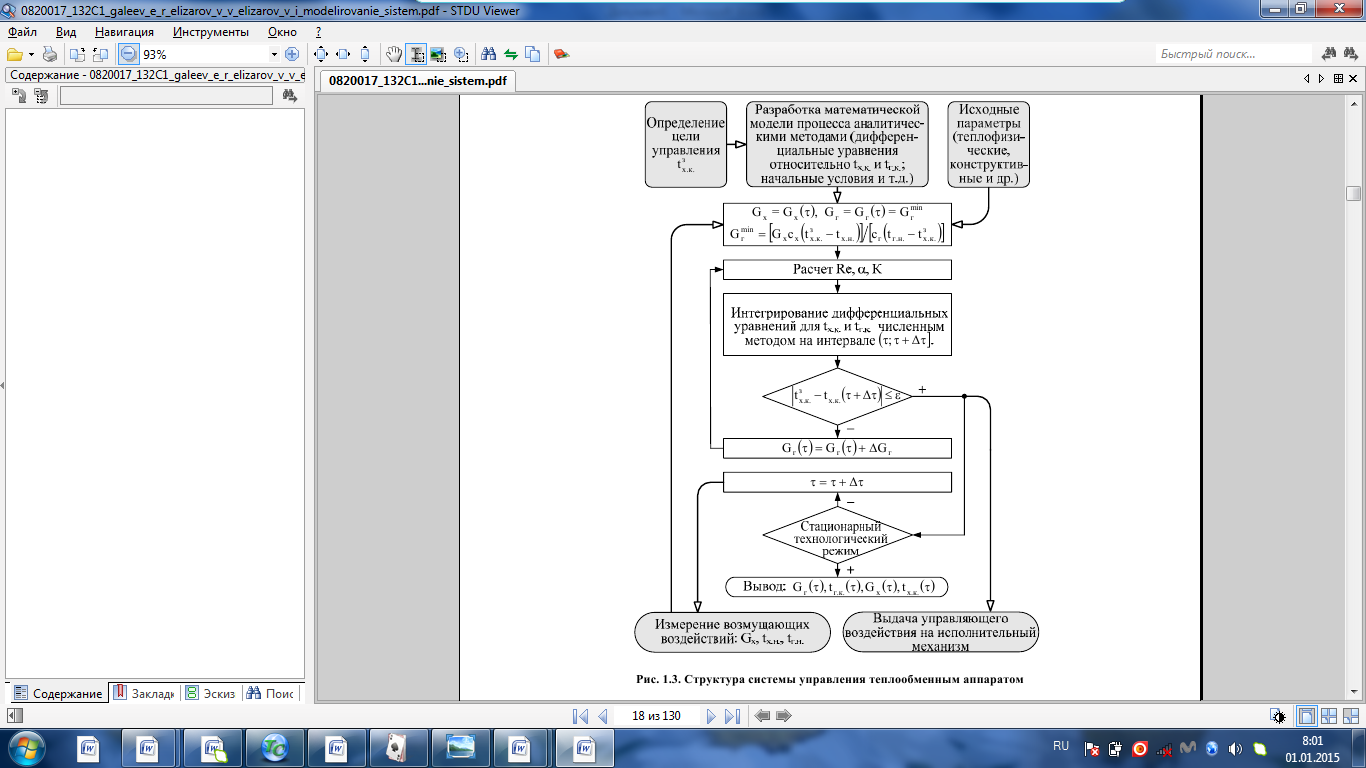 Рис. 1.3. Структура системы управления теплообменным аппаратом По формуле (1.6) рассчитывается коэффициент теплопередачи К. Далее интегрируются дифференциальные уравнения. В конце временного такта проверяется условие равенства температуры нагреваемой смеси на выходе аппарата заданному значению. Если условие выполняется, то переходят к расчету на следующем временном такте, иначе выбирается новое приближение Gг(τ) в текущем такте. 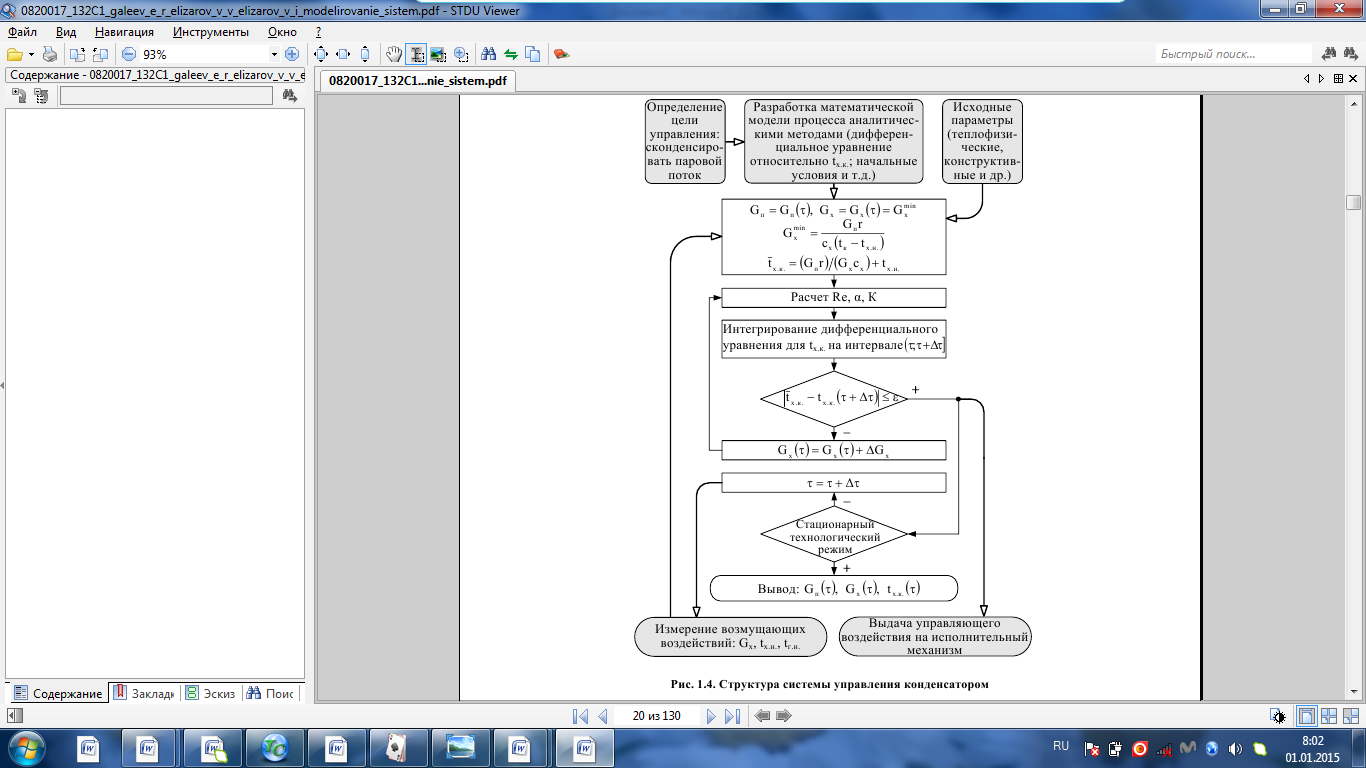 Рис. 1.4. Структура системы управления конденсатором Пусть расход нагреваемой смеси на входе теплообменника заданной конструкции условно смоделирован в виде функций времени Gх = Gх(τ). Требуется найти расход нагревающего агента Gг(τ), при котором температура нагреваемой смеси на выходе аппарата равна заданной tзх.к. в дискретные моменты времени τ = k∆τ ( k =1,2,3,...). При решении задачи управления конденсатором заданной конструкции, как правило, требуется определить расход охлаждающего агента Gx(τ) с начальной температурой tх.н., при котором полностью конденсируется паровая смесь. Возмущающими параметрами являются расход и температура паровой (газовой) смеси. Рассмотрим алгоритм поиска Gx(τ) (рис. 1.4) вдискретные моменты времени τ = k∆τ (k =1,2,3,... ). Расход паровой смеси на входе теплообменника условно смоделирован в виде функции времени Gп = Gп(τ). Известна температура tк или давление конденсации паров. Т.к. температура одного из теплоносителей остается постоянной, то динамическую модель процесса представим уравнением относительно температуры охлаждающего агента на выходе аппарата tх.к..По своей структуре уравнение аналогично выражению (1.11). Температура конденсата постоянна и равна tк. Условием окончания поиска на каждом такте является равенство температуры охлаждающего агента на выходе, рассчитанной из уравнений динамики, температуре, определяемой балансовым соотношением: 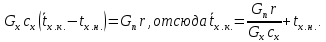 Начальные условия интегрирования дифференциальных уравнений задаются исходя из предположения о том, что аппарат до момента возникновения возмущений функционировал удовлетворительно. В этом случае: 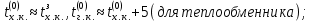 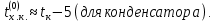 Процедура поиска управления продолжается до достижения теплообменным аппаратом стационарного (установившегося) режима работы, при котором состояние входа и выхода аппарата неизменны во времени. Варианты заданий 1а – 1г Тема курсовой работы: моделирование системы управления теплообменным аппаратом на основе анализа уравнений динамики процесса. Задание: – исследовать процесс функционирования кожухотрубного теплообменника, предназначенного для теплообмена между двумя водноорганическими растворами (оба раствора – коррозионно-активные жидкости с физико-химическими свойствами, близкими к свойствам воды); – составить динамическую модель процесса; – определить расход горячего раствора (подается в трубное пространство) в дискретные моменты времени, обеспечивающий температуру нагреваемой среды на выходе аппарата 45 оС; – зависимость расхода горячего теплоносителя, расхода нагреваемой смеси, а также температур теплоносителей на выходе аппарата от времени представить в табличном и графическом виде; – разработать презентацию курсовой работы и подготовить доклад к защите. Исходные данные и допущения: 1) длительность процесса определяется временем выхода на установившийся режим; 2) расход нагреваемой среды на входе теплообменника задан в виде функции времени Gх(τ); 3) начальные температуры нагреваемой смеси tх.н. и нагревающего агента (горячего теплоносителя) tг.н.; 4) теплофизические свойства горячего теплоносителя: плотность ρг, теплопроводность λг, динамическая вязкость µг, удельная теплоемкость cг; 5) теплофизические свойства нагреваемой смеси: плотность ρх, теплопроводность λx, динамическая вязкость µx, удельная теплоемкость cx; 6) параметры теплообменника: диаметр кожуха D, диаметр труб dт, число ходов z, число труб n, длина труб L, поверхность теплообмена F, площадь сечения потока между перегородками sп, площадь сечения одного хода по трубам sт(табл. 1.1); 7) для определения режима течения жидкости в трубном пространстве используется выражение: 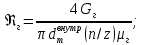 8) для определения режима течения жидкости в межтрубном пространстве используется выражение: 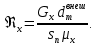 Таблица 1.1
|