Курс_Модел2_2 (1). Методические указания к выполнению курсовой работы дисциплины моделирование технологических процессов и основы оптимизации для студентов, обучающихся по направлению
 Скачать 3.02 Mb. Скачать 3.02 Mb.
|
|
Рис. 4.3. Зависимость константы скорости реакции от абсолютной температуры в аррениусовых координатах Константа А вычисляется как тангенс угла наклона прямой к оси абсцисс, постоянная В численно равна отрезку, отсекаемому прямой на оси ординат при 1 T = 0 (T = ∞). При исследовании причин зависимости скорости реакций от температуры вводят понятие энергии активации Ea (Дж/моль). Энергия активации есть минимальная избыточная энергия, которой должны обладать молекулы для протекания реакции. Обычно для химических реакций порядок величины Ea составляет десятки или сотни кДж/моль. С. Аррениус установил, что энергия активации связана с константой А простым соотношением Ea= AR, (4.5) где R – универсальная газовая постоянная. Подставив в (4.4) величину A из (4.5), получим 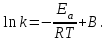 (4.6) (4.6) Дифференцируя (4.6) по температуре при Ea = const, придем к выражению 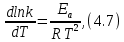 которое называется уравнением Аррениуса в дифференциальном виде. Из него путем интегрирования можно сноваполучить уравнение (4.6), где В – постоянная интегрирования. Обозначив B = ln k0, из (4.6) получим 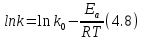 или 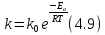 где k0 – предэкспоненциальный множитель (предэкспонент) константы скорости реакции. Выражение (4.9) называется уравнением Аррениуса в интегральном виде. Величины Ea и k0определяются природой реакции и практически не зависят от температуры. По уравнению Аррениуса константа скорости и скорость реакции экспоненциально зависят от абсолютной температуры. Энергию активации можно рассчитать по экспериментальным данным графическим или аналитическим способом. Графический способ заключается в нахождении величины A=−tgα по графику зависимости 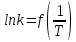 для данной реакции с последующим расчетом Ea по уравнению (4.5) (рис. 4.3). для данной реакции с последующим расчетом Ea по уравнению (4.5) (рис. 4.3).Аналитический способ предполагает применение уравнения (4.8) для двух различных температур (T2> T1; k (T2) = k2; k (T1)= k1): 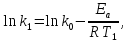 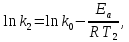 В результате вычитания второго уравнения из первого получим 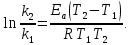 По полученному уравнению можно рассчитать энергию активации данной реакции, используя два экспериментальных значения константы скорости при двух различных температурах, или произвести пересчет константы скорости с одной температуры на другую при известной энергии активации. Математическая модель химического реактора Процесс химической реакции может проходить в кинетической области, диффузионной области и переходной области. В общем случае, когда концентрация реагента непостоянна в различных точках реактора или непостоянна во времени, материальный баланс составляют в дифференциальной форме (за объект расчета принята cA в потоке, проходящем за единицу времени) [12, 15]: 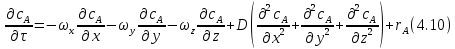 гдеcA – концентрациявеществаАвреакционнойсмеси; x, y, z – пространственные координаты; D – коэффициент диффузии; ωx, ωy, ωz – составляющие скорости потока (м/с); rA – скорость превращения исходного компонента А в целевой продукт. В зависимости от типа физико-химической системы и режима работы реактора уравнение (4.10) можно упростить. Реактор идеального смешения периодического действия (РИС-П) РИС-П применяют для простого, одностороннего, изотермического процесса. Так как в РИС-П в каждой точке объема все параметры одинаковы, то производные любогопорядка от концентрации по х, у, z равны нулю 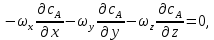 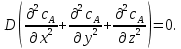 Уравнение (4.10) принимает вид полного дифференциала: 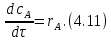 Реакторы периодического действия эффективны в случае продолжительно протекающих реакций при получении в одном и том же реакторе различных лекарственных препаратов, реактивов, красителей, когда для достижения достаточной степени превращения требуются большие затраты времени, а объем выпускаемого продукта сравнительно невелик. Реактор идеального смешения непрерывного действия (РИС-Н) РИС-Н может работать в режиме пуска, нормальной эксплуатации, останова и т.д., т.е. в нестационарном и в стационарном режимах. При большой мощности производства одного и того же продукта предпочтителен РИС-Н со стационарным (неизменным во времени) режимом. Уравнение материального баланса дляРИС-Н можно записать на основе уравнения (4.10) при условии, что 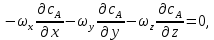 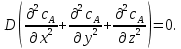 При объемной скорости (м3/с) на входе и выходе WВХ=WВЫХ=Wв стационарном режиме: 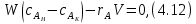 где V – объем реактора. Реактор идеального вытеснения (РИВ) Конструктивной характеристикой химического реактора вытеснения является отношение длины аппарата к его диаметру L/D >100. Реакционную смесь в аппарат подают непрерывно. Исходные продукты по мере прохождения по длине (высоте) аппарата превращаются в целевые. Химическое или физико-химическое превращение заканчивается на выходе из аппарата. Гидродинамический режим в РИВ состоит в том, что любая частица сырьевого потока движется только в одном направлении вдоль оси реактора, перемешивания продольные и по диаметру отсутствуют. Таким образом, объем реагирующих продуктов dV не смешивается с предыдущими и последующими элементами потока (поршневое движение). Состав каждого элемента потока изменяется в соответствии с термодинамикой и кинетическими особенностями рассматриваемого процесса. Уравнение (4.10) должно быть скорректировано, так как 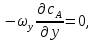 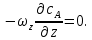 Если направление движения реакционной массы аппарата совпадает с осью х, то 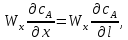 где 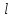 – продольная координата реактора. – продольная координата реактора.B объемеdV реактора идеального вытеснения диффузией можно пренебречь: D =0. Тогда уравнение материального баланса РИВ при нестационарном режиме имеет вид 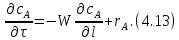 Модели реакторов с неидеальной структурой потоков Существуют две модели учета неидеальности потока, в некоторой степени приближающие расчеты к реальным процессам в реакторах. Первая из них основана на мысленной замене реального реактора некоторой последовательностью идеальных аппаратов (ячеечная модель). Вторая – на введении большего физического обоснования в системе математического описания процесса, в т.ч. с помощью математического описания процессов обратного перешивания (однопараметрическая диффузионная модель), обратного и радиального перемешивания (двухпараметрическая диффузионная модель). Ячеечная модель. Реальный аппарат разбивают на N последовательно соединенных реакторов идеального смешения (ячеек). Сумма всех ячеек равна объему проектируемого реактора. Число ячеек – единственный параметр ячеечной модели. Зная необходимое число N, рассчитывают каждую ячейку идеального смешения. Однопараметрическая диффузионная модель. В отличие от модели идеального вытеснения в диффузионной модели учитывают перемешивание реакционной смеси в осевом направлении, которое происходит в результате турбулентной диффузии. Изменение концентрации реакционного компонента в связи с появлением турбулентной диффузии описывают с применением коэффициента DT. В расчеты поэтой модели вводят допущения: по поперечному сечению реактора состав не изменяется, изменения происходят только вдоль оси аппарата; в аппарате отсутствуют застойные зоны и байпасные потоки. Уравнение, описывающее нестационарный процесс вреальном реакторе при наличии продольного перемешивания, имеет вид: 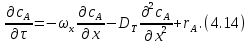 Расчет управляющих параметров реакционной установки Целью расчета реактора заданной конструкции является определение параметров процесса, которые обеспечивают максимальную степень превращения исходного вещества. Пусть в реактор подается бинарная смесь реагентов, состоящая из компонентов А1 и А2. Параметры смеси: состав (с – концентрация вещества А1, мол.доли), расход GA (моль/с).Кроме того, на вход реактора подается реагентВ, который вступает в реакцию с веществами А1 и А2: A1 + B→C, A2+ B→C. Температура реакционной смеси на входе реактора Tp(0) (К) поддерживается изменением расхода горячего теплоносителя GГ (кг/с) в теплообменник, предназначенного для нагревания реакционной смеси. Если реакция протекает с выделением тепла, то температура в изотермическом реакторе регулируется подачей холодного теплоносителя GX (кг/с). Математическое описание реакционного процесса представлено уравнениями кинетики и теплового баланса. В качестве возмущающего параметра процесса рассматривается изменение состава смеси реагентов А1и А2(изменение концентрации вещества А1). Скомпенсировать эти возмущения возможно изменением GГ, GXи температуры холодного теплоносителя TX(0) на входе реактора. 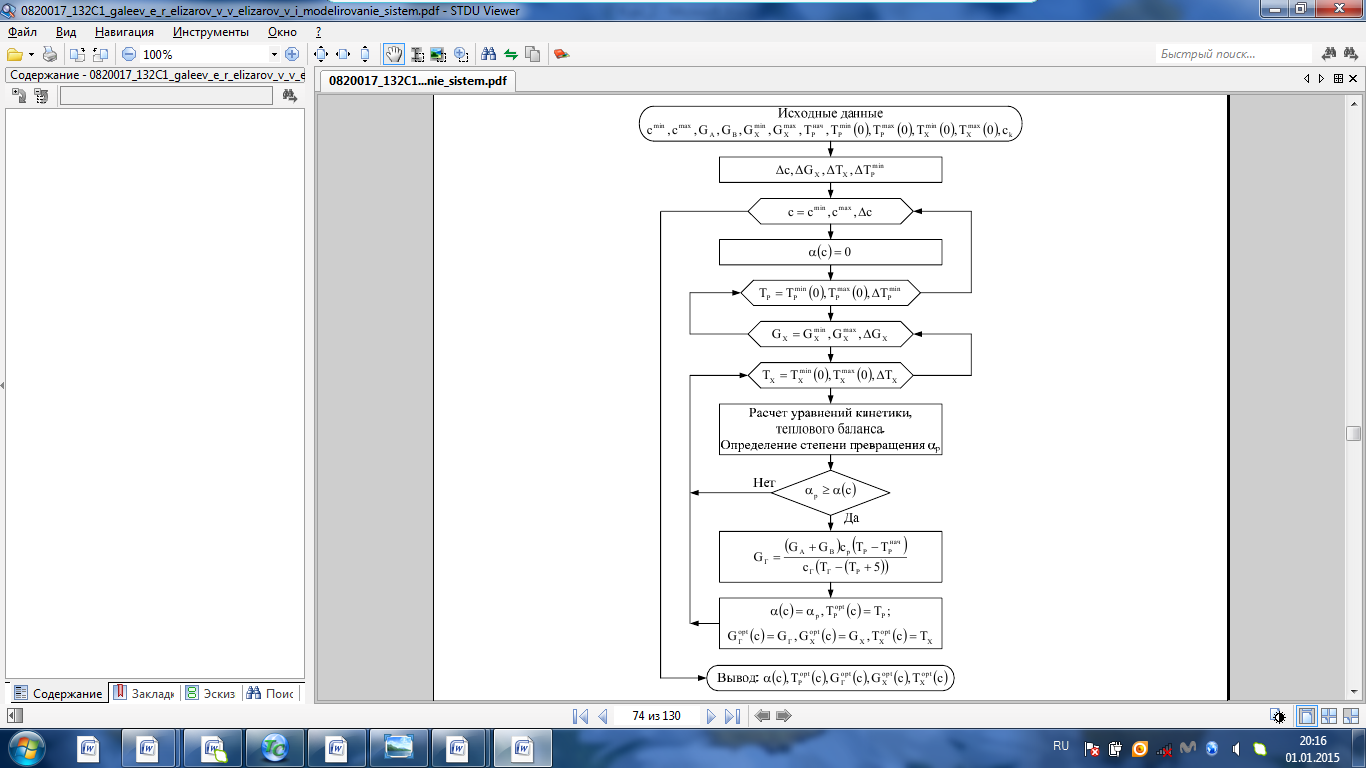 Рис. 4.4. Алгоритм расчета управляющих параметров реакционной установки Задав значение концентрации с из области возмущений (cmin,cmax) осуществляется поиск оптимальных значений GГ, GX, TX(0), при которых степень превращения веществ А1 и А2 будет максимальной (рис. 4.4). Расчет уравнений кинетики и теплового баланса проводится одним из численных методов. Расход GГ определяется с помощью уравнения теплового баланса для теплообменника, которое включает: массовые теплоемкости реакционной смеси сP и горячего теплоносителя cГ, температуры смеси на входе теплообменника TPнач и выходе TP, температуру теплоносителя на входе TГ(К). Использование аналитических зависимостей для определения управляющих параметров может быть реализовано в системе управления, структура которой приведена на рис. 4.5. 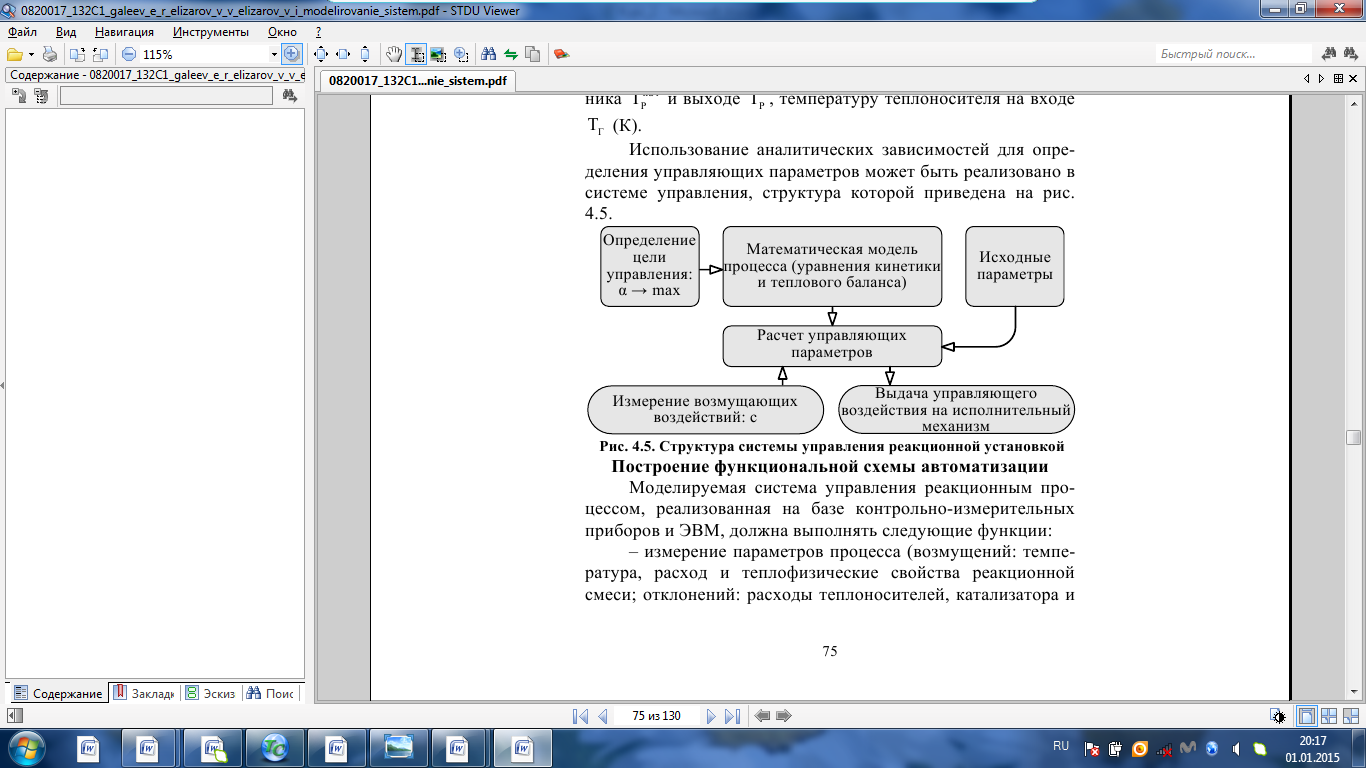 Рис. 4.5. Структура системы управления реакционной установкой Варианты заданий 4а – 4к Тема курсовой работы: моделирование системы управления реакционным аппаратом на основе анализа уравнений кинетики химической реакции. Задание: – исследовать процесс функционирования реактора, предназначенного для получения метил-третамилового эфира (МТАЭ) путем химического взаимодействия метанола с изоамиленами (2-метилбутен-1, 2-метилбутен-2) в присутствии катализатора; – для заданной области изменения состава смеси изоамиленов определить расход холодного теплоносителя в реактор, температуру теплоносителя и реакционной смеси, при которых степень превращения изоамиленов будет максимальной; – получить кинетические кривые по длине реактора для одного из составов смеси изоамиленов; – зависимость расхода нагревающего теплоносителя в теплообменник для нагревания реакционной смеси от состава смесиизоамиленов представить в табличном и графическом виде; – зависимость расхода холодного теплоносителя в реактор, температуры холодного теплоносителя от состава смеси изоамиленов представить в табличном и графическом виде; – разработать презентацию курсовой работы и подготовить доклад к защите. Исходные данные и описание процесса: 1) Технологическая схема установки состоит из теплообменника и реактора. 2) В целях повышения степени превращения реакционная смесь предварительно нагревается в теплообменнике. Такимобразом, температура реакционной смеси на входе реактора поддерживается изменением расхода горячего теплоносителя в теплообменнике. 3) Реакция взаимодействия изоамиленов с метанолом протекает с выделением тепла, ее проводят в трубчатом реакторе. Для поддержания требуемого температурного режима в межтрубное пространство реактора подается холодный теплоноситель. 4) Реакция описывается системой дифференциальных уравнений: 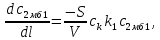 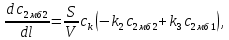 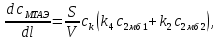 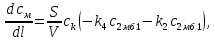 где ci– объемные мольные концентрации компонентов реакционной смеси (i=1 – 2-метилбутен-1, i = 2 – 2-метилбутен-2, i = 3 – МТАЭ, i = 4 – метанол); ck – объемная мольная концентрации катализатора; l – продольная координата реактора (дм); S – свободное сечение трубки реактора; V – объемный расход реакционной смеси в трубке (л/с). 5) Изменение температур реакционной смеси TP и холодного теплоносителя TX в реакторе определяются с помощью уравнений теплового баланса: 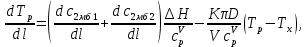 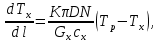 где ∆H – тепловой эффект реакции; cPV – изобарная теплоемкость реакционной смеси; K – коэффициент теплопередачи от реакционной массы к теплоносителю через стенки трубки; N, D – количество и диаметр трубок в реакторе; GX – массовый расход теплоносителя; сX – массовая теплоемкость теплоносителя. 6) Константы скорости реакции ki описываются уравнением Аррениуса: 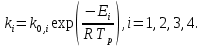 где k0,i – предэкспоненциальныймножитель, Ei– энергия активации компонентов, вступающих в реакцию, R – универсальная газовая постоянная. 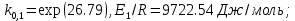 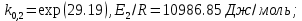 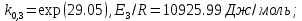 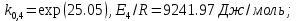 7) Температура реакционной смеси и горячего теплоносителя на входе теплообменника Tpнач, TГ; теплоемкость реакционной смеси и горячего теплоносителя cP, cГ; длина реактора L; пределы изменения температуры реакционной смеси на входе реактора Tpmin(0) ÷Tpmax(0); пределы изменения температуры теплоносителя на входе реактора TXmin(0) ÷TXmax(0); расход смеси изоамиленов GA; концентрация 2-метил-бутена-1 в смеси изоамиленовcmin÷cmax; расход метанола GB; пределы изменения расхода теплоносителя GXmin÷GXmin(табл. 4.1). 8) Плотности компонентов: ρ2мб1 = 650 кг/м3, ρ2мб1 = 662 кг/м3, ρмтаэ = 743 кг/м3, ρм = 791 кг/м3. Таблица 4.1
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
