Практическая работа. главное. Методическое пособие для учителя Авторский коллектив фгаоу дпо Академия Минпросвещения России

• Название: Методическое пособие для учителя Авторский коллектив фгаоу дпо Академия Минпросвещения России
• Анкор: Практическая работа
• Дата: 11.04.2022
• Размер: 2.16 Mb.
• Имя файла: главное.docx
• Тип: Методическое пособие; #461728
• страница: 3 из 9

Классификация задачи (вопрос 1)

Описание	Применить вычисления с процентами в рамках данной ситуации в реальном мире
Область математического содержания	Количество
Контекст	Применять
Познавательная деятельность	Научный

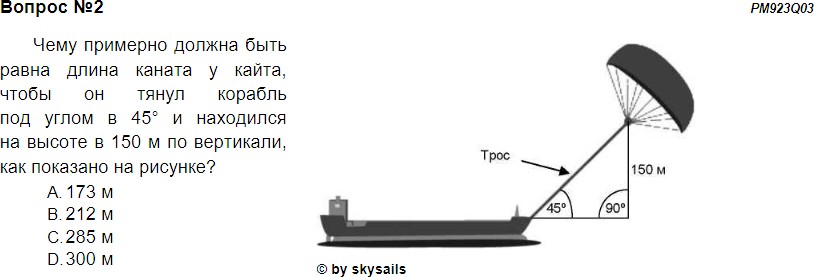Рис. 3. Пример задачи международного исследования математической грамотности PISA–2012

Классификация задачи (вопрос 2)

Описание	Использовать теорему Пифагора в рамках геометрического содержания реальной ситуации
Область математического содержания	Пространство и форма
Контекст	Применять
Познавательная деятельность	Научный

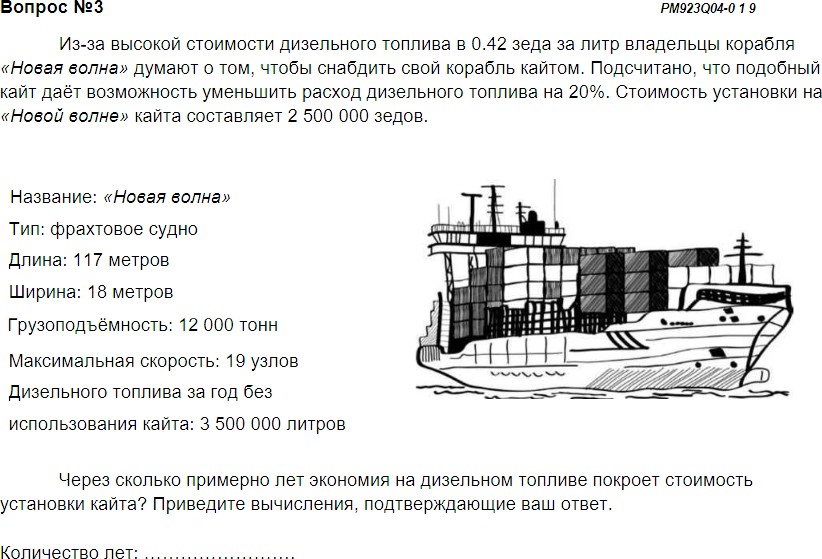Рис. 4. Пример задачи международного исследования математической грамотности PISA–2012
Классификация задачи (вопрос 3)

Описание	Решить ситуацию в реальном мире, включающую экономию затрат и расхода топлива
Область математического содержания	Изменения и зависимости
Контекст	Формулировать
Познавательная деятельность	Научный

2. Особенности заданий PISA и оценка уровня математической грамотности

   1. Особенности заданий на формирование и оценку математической грамотности

В исследованиях, которые ставят перед собой задачу оценивания учебных достижений учащихся, традиционную для мониторинговых исследований в области оценивания предметной подготовки учащихся, разработка инструментария обычно осуществляется на основе содержания программы по математике и программных требований к подготовке учащихся (примером такого исследования является существующая до 2021 года концепция TIMSS). Учащимся предлагаются учебные задачи разного уровня сложности, позволяющие проверить умение применять знания в стандартных или нестандартных учебных ситуациях. При разработке исследования PISA использован другой подход: определены математические знания и умения,

которые необходимы для решения повседневных задач.

К особенностям заданий исследования PISA относятся следующие:

1. 
   задача, поставленная вне предметной области и решаемая с помощью предметных знаний, например, по математике;
   
2. 
   контекст заданий близок к проблемным ситуациям, возникающим в повседневной жизни;
   
3. 
   вопросы изложены простым, ясным языком и, как правило, немногословны;
   
4. 
   требуют перевода с обыденного языка на язык предметной области (математики, физики и др.);
   
5. 
   формат заданий постоянно меняется, что исключает стратегию
   

«натаскивания».

Для успешного понимания и решения контекстных проблем, предложенных в тестах исследования PISA, требуется владеть определенной совокупностью
математических понятий, процедур, фактов и инструментов на определенном уровне понимания и глубины усвоения. Такая совокупность была определена на основе анализа стандартов по математике 11 развитых стран мира, в числе которых были страны, показавшие в исследованиях PISA самые высокие результаты. Учитывалось, какие знания эти страны считали реально достижимыми и необходимыми для обеспечения учащимся возможности начать работать или поступить в институты для получения высшего образования, а также достаточно ли этих знаний для того, чтобы 15-летние учащиеся были конструктивными, заинтересованными и размышляющими членами современного общества.

Разработчиками концепции исследования составлен следующий перечень математических тем, владение которыми необходимо для успешного выполнения тестовых заданий.

Функции:понятие функции, разнообразные формы их описания и представления: словесная, символьная, табличная и графическая.

Алгебраические выражения: словесная интерпретация и операции, работа со значениями переменных.

Уравнения и неравенства: линейные уравнения, системы линейных уравнений и неравенства, простые квадратные уравнения, аналитические и неаналитические методы решения (например, метод «проб и ошибок»).

Система координат: представление и описание данных, их расположения и зависимостей.

Отношенияврамкахгеометрическогообъектаисредигеометрических объектоввдвумерномитрехмерномпространстве.Пространственныефигурыиихсвойства,формулывычисленияплощадейповерхностииобъема. Измерения: количественная характеристика свойств фигур и объектов,

между фигурами и объектами.

Числаиединицыизмерения.
Арифметические и алгебраические операции: смысл и свойства этих операций и принятых соглашений (например, законов), включая возведение чисел в натуральную степень и извлечение простых квадратных корней.

Проценты,отношенияипропорции: вычисление их величины, применение пропорций и прямо пропорциональных отношений для решения проблем.

Оценка: отвечающие поставленной цели приближенные значения величин и числовых выражений, включая значимые цифры и округление.

Принципыподсчетов: простые сочетания и перестановки (в расчете на способ перебора вариантов).

Набор данных, представление и интерпретация: природа, происхождение, наборы разнообразных данных, различные способы их представления и интерпретации.

Изменчивость данных и ее описание: такие понятия, как изменчивость, распределение, центральная тенденция набора данных, способы описания и интерпретации этих данных в количественных выражениях.

Выборкиисоставлениевыборок: понятие выборки и выбора из совокупностей данных, включая простые выводы на основе свойств выборок.

Случайность и вероятность: понятие случайного события, случайное изменение и его представление, частота и вероятность событий, основные аспекты понятия вероятности.

Также были выделены ключевые компетенции, необходимые для форм овладения математической грамотностью:

• 
  коммуникация;
  
• 
  математическое моделирование;
  
• 
  представление;
  
• 
  рассуждения и аргументы;
  
• 
  разработка стратегии решения проблем;
  

• 
  использование символического, формального и технического языка и операций;
  
• 
  использование математических инструментов.
  

Тестовые задания по математике в исследовании PISA предлагаются учащимся в контекстной форме. К каждому заданию дается описание некоторой ситуации и предлагается от 1 до 6 вопросов, в которых ставятся проблемы, которые надо решить, пользуясь информацией, предложенной в описании ситуации и в самом вопросе. Поэтому успешность выполнения этих заданий существенно зависит не только от предметных знаний, но и от овладения учащимися стратегиями смыслового чтения и умения работать с текстом. К ним следует отнести, например, такие виды деятельности, как:

• 
  решать учебно-познавательные и учебно-практические задачи, требующие полного и критического понимания текста;
  
• 
  удерживать условия задания в процессе решения;
  
• 
  самоконтроль за выполнением условий (ограничений) в описании ситуации при нахождении решения и интерпретации полученного решения в рамках предложенной ситуации;
  
• 
  работать с информацией, представленной в различной форме (текста, таблицы, диаграммы столбчатой или круговой, схемы, рисунка, чертежа с обозначением видимых и невидимых элементов геометрической фигуры) в контексте конкретной проблемы.
  

Кроме того, математическая грамотность существенно зависит от овладения познавательными универсальными действиями логического и алгоритмического характера, общим приемом решения задач, которые в значительной степени формируются при изучении математики.

Данный перечень не выходит за рамки требований к математической подготовке выпускников основной российской школы, представленных в Федеральном государственном стандарте и в Примерной основной

образовательной программе образовательного учреждения.
Распределение заданий в исследовании PISA выглядит следующим образом:

• 
  25% – формулировать;
  
• 
  25% – интерпретировать;
  
• 
  50% – применять.
  

Приведем пример задания для формирования и оценки математической грамотности [2], в котором используются различные виды познавательной деятельности и формы ответов (рис. 5, 6, 7).


Рис. 5. Пример задания для формирования и оценки математической грамотности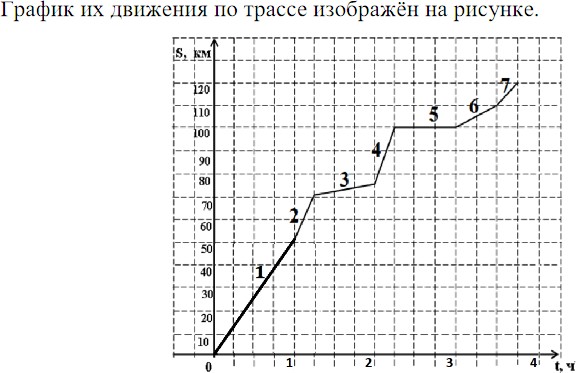


Рис. 6. Пример задания для формирования и оценки математической грамотности




Рис. 7. Пример задания для формирования и оценки математической грамотности
В исследование PISA–2022 будут включены новые темы – это явления роста (изменения и зависимости), геометрическая аппроксимация (пространство и формы), компьютерное моделирование (количество), принятие решений в условиях неопределенности (неопределенность и данные).

Появятся и новые типы заданий, которые представлены на рисунке 8.


Рис. 8. Новые типы заданий в исследовании PISA Пример задания PISA-2022 [16].

Самое короткое расстояние между двумя точками – отрезок прямой. Однако двигаться по прямой линии в городе не всегда представляется возможным. Посмотрите на карту, изображенную на рисунке. Серые линии обозначают дороги, а квадратные синие блоки – здания (рисунок 9).

Рис. 9. Пример задания PISA-2022

Исследуем различные стратегии планирования маршрута из одной точки города в другую (рис. 10, 11, 12).

Энн, Боб и Кори предлагают различные идеи нахождения самого короткого маршрута из точки A в точку B.

Энн всегда движется вправо или вверх, оставаясь ниже красной линии, соединяющей точки A и B, как можно ближе к ней (зеленая линия).

Боб всегда движется вправо или вверх, стараясь пересечь красную линию, соединяющую точки A и B (оранжевая линия).

Кори всегда движется вправо или вверх, оставаясь выше красной линии, соединяющей точки A и B, как можно ближе к ней (фиолетовая линия).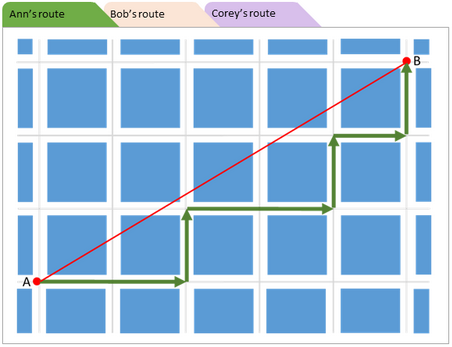


Рис. 10. Пример задания PISA-2022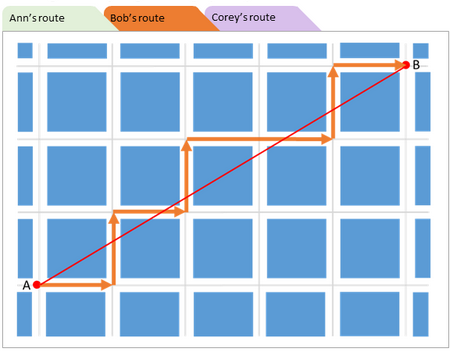




Рис. 11. Пример задания PISA-2022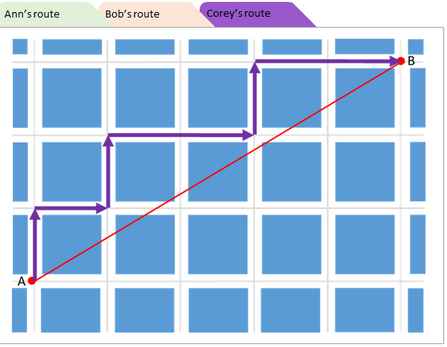

Рис. 12. Пример задания PISA-2022

С помощью мыши перемещайте точку А на разные отмеченные перекрестки дорог – для каждой позиции будет A показан маршрут для каждой стратегии доступа к В и соответствующее расстояние (рис. 13).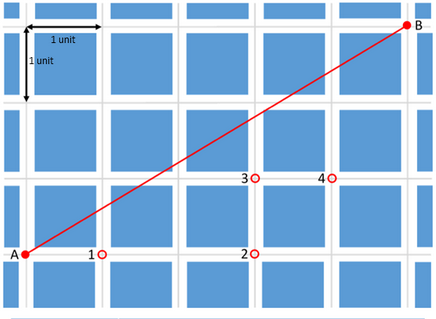



Рис. 13. Пример задания PISA-2022

Месторасположение точки А	Расстояние от A до B
	Маршрут Энн	Маршрут Боба	Маршрут Кори
1
2
3
4

Вы заметите, что независимо от расположения точки A и маршрута, длина от А до B остается одинаковой.

Объясните, почему при применении любой из трех стратегий длина маршрута остается одинаковой.