Практическая работа. главное. Методическое пособие для учителя Авторский коллектив фгаоу дпо Академия Минпросвещения России
 Скачать 2.16 Mb.
|
Особенности заданий Международного исследования PISA-2022Весной 2022 года российские школьники вновь примут участие в международном мониторинговом исследовании PISA. Приоритетным направлением предстоящего исследования будет математическая грамотность в обновленной диагностической модели (рис. 26). 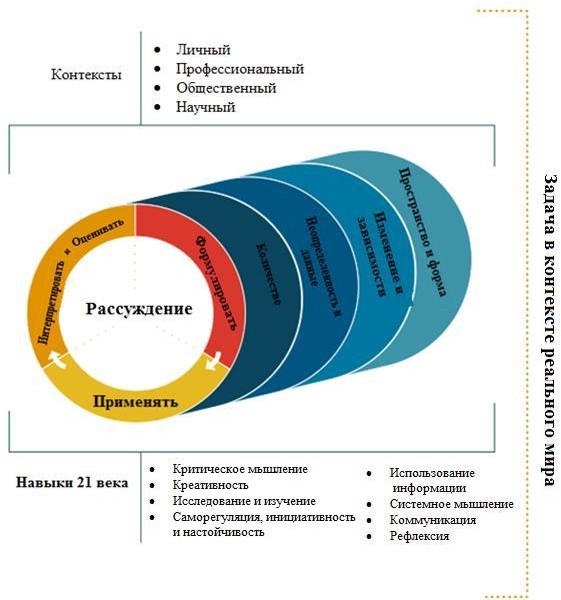 Рис. 26. Диагностическая модель математической грамотности PISA-2022 [7] Анализ данной модели показывает, что специальным предметом проверки станет способность 15-летних подростков на разных этапах применения метода математического моделирования математически рассуждать о возможности объяснения или обоснования тех или иных явлений и процессов с использованием математики, о полноте входной количественной информации для получения выводов, о правильности выбора той или иной математической модели, об обоснованности высказанных суждений и др. В школьном курсе математические рассуждения в основном связаны с поиском способа решения задачи и оценкой утверждений в категоричной дихотомической шкале: истина/ложь. В обыденной жизни оценки высказанных суждений часто бывают более мягкими, учитывающими, что для установления истинности или ложности суждения приведенной или доступной информации может быть недостаточно, а также что множество объектов высказывания, указанных в предложении, шире, чем область его истинности. В этом случае используется дополнительная категория: иногда истинно. Нельзя сказать, что при изучении математики в школе учащиеся не встречаются с такими ситуациями. Достаточно вспомнить задачи на решение уравнений, неравенств, проверку того, есть ли среди заданных чисел те, которые являются корнями уравнения или решениями неравенства, на установление множества чисел для которых данное равенство или неравенство является тождеством. Единственным отличием является отнесенность объектов высказывания не только к множеству математических объектов, но и реальных объектов, явлений или процессов. Для того чтобы осмыслить способы выполнения подобных заданий обратимся к математической логике. Пусть имеется предикат 𝑃(𝑥), то есть некоторое утверждение 𝑃 об объекте 𝑥 из множества 𝐴. Утверждение 𝑃(𝑥) истинно всегда, если доказано, что справедливо высказывание ∀𝑥 ∈ 𝐴: 𝑃(𝑥), то есть для любого объекта из множества 𝐴 утверждение 𝑃(𝑥) истинно. Утверждение 𝑃(𝑥) истинно иногда, если во множестве А найдены два таких элемента 𝑥1; 𝑥2 ∈ 𝐴, что 𝑃(𝑥1) истинно, а 𝑃(𝑥2) ложно. Утверждение 𝑃(𝑥) истинно никогда, если доказано, что справедливо высказывание ∃̅𝑥 ∈ 𝐴: 𝑃(𝑥). Рассмотрим способы решения подобных задач на конкретном примере из демоверсии заданий PISA-2022.
Для проверки первого утверждения удобно использовать геометрическую модель изменения роста девочки от 0 до 14 лет. Пусть ℎ0 − рост девочки в момент рождения, ℎ14 − ее рост в четырнадцать лет. Тогда очевидно, что справедливым является высказывание, что для любого значения ℎ > 0 справедливо неравенство 0 < ℎ14 < ℎ (рис. 27). Следовательно, 14 2 14 данное утверждение истинно всегда. 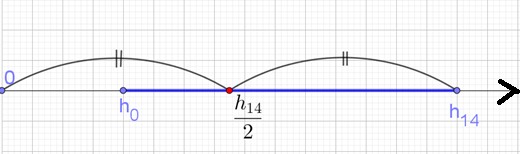 Рис. 27 Для проверки второго утверждения достаточно вспомнить, что в младших классах есть девочка, которая выше знакомой четырнадцатилетней девочки, и есть другая, которая ее ниже. 
Утверждение 1 истинно иногда, так как если взять число 2 и умножить его самого на себя, то получим четное число 4, а если взять число 3 и умножить его самого на себя, то получим нечетное число. Утверждение 2 истинно всегда, так как четным числом по определению называется целое число, делящееся на два. Обозначим произвольное целое число за 𝑛. Тогда результатом его удвоения будет выражение 2𝑛, которое делится на 2, следовательно, является четным числом. Утверждение 3 истинно никогда, так как произвольное целое нечетное число можно представить в виде 2𝑛 + 1, 𝑛 ∈ 𝑍. Если взять его половину, то получим 𝑛 + 0,5 ∉ 𝑍. Утверждение 4 истинно всегда, так как правая часть получена в результате умножения и деления выражения,  Задание 3. Каждое из представленных ниже утверждений истинно иногда.Приведите пример, когда оно истинно, и пример, когда оно ложно.
Приведенные примеры показывают, что постановка задач на оценку утверждений в категориях истинно всегда, иногда или никогда возможна как в математическом, так и в житейском контекстах. Включение подобных заданий в процесс обучения математике позволит учащимся лучше осмыслить условия истинности теорем и вводимых формул, а также покажет, в какихслучаях необходимо проведение доказательства, а в каких достаточно аргументировать свою позицию приведением примеров и контрпримеров. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
