Практическая работа. главное. Методическое пособие для учителя Авторский коллектив фгаоу дпо Академия Минпросвещения России
 Скачать 2.16 Mb. Скачать 2.16 Mb.
|
Что такое математическая грамотность и почему необходимо формировать математическую грамотность у современныхшкольников В исследовании PISA математическая грамотность определяется как «способность индивидуума проводить математические рассуждения и формулировать, применять, интерпретировать математику для решения проблем в разнообразных контекстах реального мира» [15]. Умение «формулировать ситуации математически» включает способность распознавать и выявлять возможности использовать математику, принять имеющуюся ситуацию и трансформировать ее в форму, поддающуюся математической обработке, создавать математическую модель, отражающую особенности описанной ситуации. Умение «применять математику» рассматривается как способность применять математические понятия, факты, процедуры, рассуждения и инструменты для получения решения или выводов. Эта деятельность включает выполнение математических процедур, необходимых для получения результатов и математического решения (например, анализировать информацию на математических диаграммах и графиках, работать с геометрическими формами в пространстве, анализировать данные). Работать с моделью, выявлять закономерности, определять связи между величинами и формулировать математические аргументы. Умение «интерпретировать» подразумевает способность размышлять над математическим решением или результатами, интерпретировать и оценивать их в контексте реальной проблемы. Эта деятельность включает перевод математического решения в контекст реальной проблемы, оценивание реальности математического решения или рассуждений по отношению к контексту проблемы. Этот процесс охватывает и интерпретацию, и оценку полученного решения или определение того, что результаты разумны и имеют смысл в рамках предложенной ситуации. Каждый из этих мыслительных процессов опирается на математические рассуждения, поэтому разработчики концепции исследования PISA-2022 дополнили их рассуждениями. Это означает, что учащимся потребуется продемонстрировать, как они умеют размышлять над аргументами, обоснованиями и выводами, над различными способами представления ситуации на языке математики, над рациональностью применяемого математического аппарата, над возможностями оценки и интерпретации полученных результатов с учетом особенностей предлагаемой ситуации. Каждое задание на оценку математической грамотности включает контекст. Контекст задания – особенности и элементы окружающей обстановки, представленные в задании в рамках описанной ситуации. Личный контекст обычно связан с повседневной личной жизнью учащегося (при общении с друзьями, занятиях спортом, покупками, отдыхом, повседневным бытом), его семьи, его друзей и сверстников. Проблемы, которые предлагаются в профессиональных контекстах, связаны со школьной жизнью или трудовой деятельностью. Общественные контексты связаны с жизнью общества (местного, национального или всего мира). Ситуации, связанные с жизнью местного общества, касаются проблем, возникающих в ближайшем окружении учащихся. Контексты, отнесенные к научным, обычно связаны с применением математики к науке или технологии, явлениям физического мира. Математическое содержание, которое используется при конструировании заданий, сконцентрировано вокруг четырех фундаментальных идей. Изменение и зависимости – задания, связанные с математическим описанием зависимости между переменными в различных процессах, относятся к алгебраическому материалу. Пространство и форма – задания, относящиеся к пространственным и плоским геометрическим формам и отношениям, т.е. к геометрическому материалу. Количество – задания, связанные с числами и отношениями между ними, в программах по математике этот материал чаще всего относится к курсу арифметики. Неопределенность и данные – эта область охватывает вероятностные и статистические явления и зависимости, которые являются предметом изучения разделов статистики и вероятности. Школьники России показывают средние результаты, занимая в рейтинге места с 27 по 35. Одной из причин является то, что для их оценки используются не типичные учебные задачи, характерные для традиционных систем обучения и мониторинговых исследований математической подготовки, а близкие к реальным проблемные ситуации, представленные в некотором контексте и разрешаемые доступными учащемуся средствами математики. На рисунке 1 представлена диагностическая модель математической грамотности. 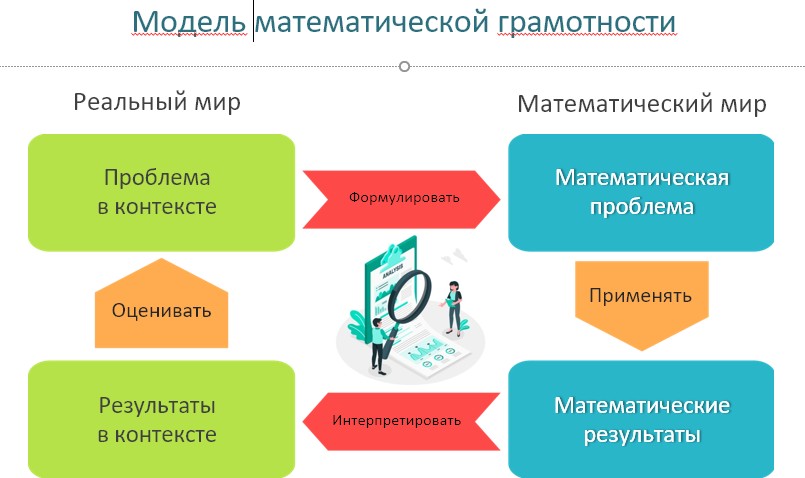 Рис. 1. Диагностическая модель математической грамотности Рассмотрим примеры задач, которые использовались в международном исследовании PISA в 2012 году [13] (рис.2, 3, 4). 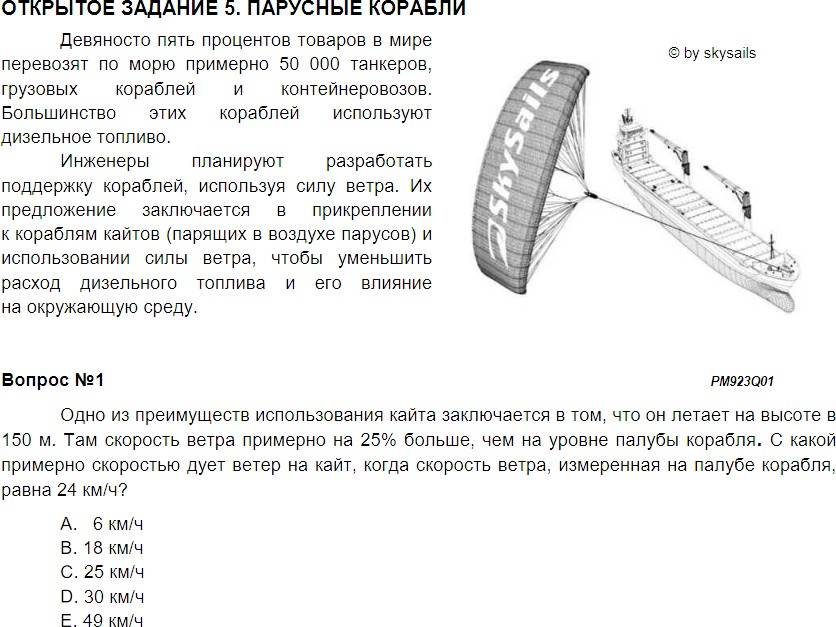 Рис. 2. Пример задачи международного исследования математической грамотности PISA–2012 |
