Лекции 2 курс СПО математика 48 часов. лекции 2 курс. Методическое пособие по дисциплине математика г. Балахна 2021г Данное методическое пособие предназначено для студентов, обучающихся по специальностям

• Название: Методическое пособие по дисциплине математика г. Балахна 2021г Данное методическое пособие предназначено для студентов, обучающихся по специальностям
• Анкор: Лекции 2 курс СПО математика 48 часов
• Дата: 11.02.2022
• Размер: 1.81 Mb.
• Имя файла: лекции 2 курс.doc
• Тип: Методическое пособие; #358225
• страница: 3 из 8

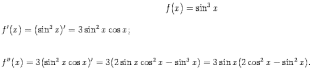П ример 1:

Найти вторую производную функции .

Первая производная равна

далее находим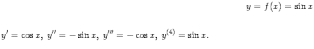

             

Пример 2.   Найти вторую и третью производные функции

Тогда

Применение первой и второй производной для исследования функции
Возрастание и убывание функции
Пусть на отрезке [a,b] определена непрерывная функция f(x),имеющая внутри отрезка конечную производную. Тогда, для того чтобы f(x) была возрастающей (убывающей) на [a,b], достаточно выполнение условия

>0 ( <0 ) для всех Х из (a,b)

Пример 1:

Дана функция у = х³ – 3х² Определить, возрастает или убывает функция в точках х = -1, х = 0, х = 2

Решение:

Дифференцируем данную функцию х² – 6х

При х = -1 получаем f ' (-1) = 10>0 т.е. ф-ция возрастает.

При х = 0 имеем f ’(0) = 0 в этом случае функция может возрастать, убывать или иметь экстремум.

При х = 2 f ‘(2)=-2< 0 т.е функция убывает

Пример 2:

Определить возрастает или убывает данная функция в указанных точках.

У=х² , при х = -3, х = -1, х=4

у = х³ при х = -1, х=3, х=5
Нахождение экстремума функции
Первое правило:

1. Продифференцировать данную функцию

2. Найти критические точки, т.е точки, в которых либо =0, либо не существует. В этих точках возможен экстремум.

3. Выяснить знак производной в окрестности каждой критической точки:

• 
  если слева от точки производная >0, а справа <0, то функция в этой точке имеет максимум;
  
• 
  если слева от точки производная <0, а справа >0, то функция в этой точке
  

имеет минимум

• 
  если слева и справа от точки производная имеет один и тот же знак, то функция в этой точке не имеет экстремума
  

Пример 3:

Исследовать функцию у = х²- 3х на экстремум по первому правилу

Решение:

1.у' = 2х-3

2.Решаем уравнение у' = 0 2х-3=0, х=1,5

Экстремум возможен только в этой точке, т.к. производная существует во всей области определения функции

3. Находим знак производной слева и справа от этой точки ( х= 1,5)

у' ( 0) = -3 <0 у' ( 2)=1 >0

т.к. слева от х=1,5 производная отрицательна, а справа положительна, то функция имеет минимум
Второе правило:

1. Продифференцировать данную функцию

2. Найти критические точки

3. Найти вторую производную в критических точках:

• 
  если y’’(x₀)< 0, то функция имеет в точке x₀ максимум;
  
• 
  если y’’(x₀) > 0, то минимум
  
• 
  если y’’(x₀) = 0 или не существует, то в этом случае следует пользоваться первым правилом
  

Пример 4:

Исследовать функцию у = х³ + 2х² на экстремум по второму правилу

Решение:

Дифференцируем данную функцию х² + 4х

Находим критические точки, где

3х² + 4х =0 х₁ = 0 х₂ = -4/3

Вычисляем вторую производную y’’ = 6x + 4

Определяем знак y’’ в точках х₁ и х₂ .

y’’(0) = 4 > 0 - минимум

y’’(-4/3) = - 4 < 0 - максимум

Исследование кривых на выпуклость, вогнутость


Пусть – функция, дифференцируемая на интервале . Рассмотрим кривую, являющуюся графиком функции .

Кривая, заданная функцией , называется выпуклой на интервале , если все точки кривой лежат ниже любой ее касательной на этом интервале.

Кривая называется вогнутой на интервале , если все точки кривой лежат выше любой ее касательной на этом интервале.

Точка кривой M₀(x₀, f(x₀)), отделяющая выпуклую ее часть от вогнутой, называется точкой перегиба.

Для того, чтобы кривая в данной точке была выпукла, достаточно, чтобы вторая производная функции в этой точке была отрицательна, т. е.

Для того, чтобы кривая в данной точке была вогнута, достаточно, чтобы вторая производная функции в этой точке была положительна, т. е.
Исследование кривых на перегиб
1-е правило

- чтобы кривая имела перегиб при х = х₀ необходимо, чтобы вторая производная в точке х₀ либо обращалась в нуль, либо не существовала

- чтобы кривая имела перегиб при х = х₀ достаточно, чтобы слева и справа от точки х₀ вторая производная имела разные знаки

2-е правило

- чтобы кривая имела перегиб при х = х₀ достаточно, чтобы вторая производная в точке х₀ либо обращалась в нуль, а третья производная в этой точке была отлична от нуля
Пример 5.

Определить направление выпуклости и точки перегиба кривой

Решение

- область определения - вся ось абсцисс; область непрерывности - вся ось абсцисс

- находим первую производную и вычисляем вторую производную

Ищем точки х из области определения функции, в которых или не существует.



Вторая производная равна нулю в точках . Эти точки являются искомыми, так как область определения и область непрерывности данной кривой есть вся ось абсцисс. Других точек х, которые могли бы быть абсциссами точек перегиба, нет, так как существует всюду.

Исследуем найденные точки, определяя знак слева и справа от каждой из них. Результаты исследования запишем в таблицу, подобную той, которая составляется при отыскании точек экстремума

Таблица

 

x		0	(0, 1)	1
		0		0
	выпукла	нет перегиба	выпукла	точка перегиба	вогнута

 

Пример 6.

Дана кривая у = ( х³ – 21 х² )/2. Найти точки перегиба

Решение:

Находим первую производную у’ =1/2 (3х² – 42х)

Вычисляем вторую производную

У” = 1/2  (6х -42) =3(х – 7)

Вторая производная равна нулю в точке х = 7 ( 3(х-7)=0 )

Т.к. вторая производная существует во всей области определения функции, то перегиб может быть лишь при х = 7

x	(- , 7)	7	(7, +)
		0
	выпукла	перегиб	вогнута

Асимптоты
При исследовании функции часто приходится устанавливать вид ее графика (а значит, и характер функции) при неограниченном удалении точки графика от начала координат (при стремлении переменной точки в бесконечность). При этом важным случаем является тот, когда график функции при удалении его переменной точки в бесконечность неограниченно приближается к некоторой прямой.

Если , то прямая является асимптотой графика (при ). Эта асимптота параллельна оси Ox и называется горизонтальной асимптотойАналогично, прямая является асимптотой графика y = f(x) (при ), если .

 

Рассмотрим асимптоты, параллельные оси Oy.

Прямая x=x₀ называется вертикальной асимптотой, если хотя бы один из пределов , , является бесконечным

Следовательно, для отыскания вертикальных асимптот нужно найти точки разрыва функции второго рода.

Пример 7. Найти вертикальные асимптоты для функции .

Решение

Функция определена и непрерывна во всех точках числовой оси, за исключением точки x₀ = 2, в которой функция терпит разрыв,

= –¥, = +¥. Следовательно, прямая х=2 является вертикальной асимптотой для графика y = . Кроме того, = 0 и = 0, следовательно, прямая y = 0 является горизонтальной асимптотой при и при .

 

Прямая называется наклонной асимптотой функции , если функцию можно представить в виде f(x)=kx + b

Определим числа k и b.



Определим коэффициент .



Если хотя бы один из пределов не существует, то при кривая не имеет наклонной асимптоты.

Аналогично решается вопрос об асимптотах при .