Лекции 2 курс СПО математика 48 часов. лекции 2 курс. Методическое пособие по дисциплине математика г. Балахна 2021г Данное методическое пособие предназначено для студентов, обучающихся по специальностям
 Скачать 1.81 Mb.
|
Неопределенный интеграл и его свойстваФункция F(x) называется первообразной функции f (х) на интервале (а; b), если выполняется равенство  Из этого определения следует, что для нахождения первообразной необходимо по заданной функции f(x ) найти функцию F(x), производная которой равна f(x). Пример: Найти первообразную функцию для функции f(x) =cosx Решение: Первообразной функции f(x) =cosxявляется функция F(x) = sin x, так как F’(x) = (sin x)’ = cos x = f(x) Первообразными будут также любые функции F(x) = sin x + C, где С – постоянная величина, так как F’(x)=(sinx +C)’ = cosx = f(x) Множество всех первообразных функций F(x) + C для функции f(х) называется неопределённым интегралом от функции f(х) и обозначается символом  , где C - произвольная постоянная. Функцию f(x) принято называть подынтегральной функцией, произведение f(x) dx - подынтегральным выражением, х – переменная интегрирования.Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции Геометрически неопределенный интеграл представляет собой множество интегральных кривых y=F(x) + C, каждому числовому значению С соответствует определенная кривая. График каждой кривой называется интегральной кривой. Cвойства неопределенного интеграла: 1. Дифференциал от неопределенного интеграла равен подинтегральному выражению  2. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной  3. Постоянный множитель можно выносить за знак интеграла  4. Неопределенный интеграл от алгебраической суммы конечного числа непрерывных функций равен алгебраической сумме интегралов от этих функций  Таблица основных неопределённых интегралов               Пример 1. 1. Вычислить неопределенный интеграл 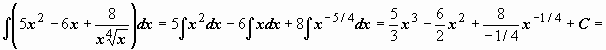  Пример 2. 1. Вычислить неопределенный интеграл  Пример 3. Подведение под знак дифференциала постоянного слагаемого 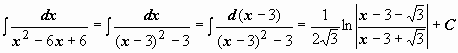 Пример 4. Подведение под знак дифференциала постоянного множителя  Пример 5.  Замена переменной в неопределённом интеграле (интегрирование подстановкой) Если интеграл  не может быть вычислен непосредственно по основным формулам, то введением новой независимой переменной во многих случаях удается преобразовать подинтегральное выражение f(x)dx. При этом интеграл приводится к табличному или к такому, прием вычисления которого уже известен. Замена переменной и составляет существо метода, называемого методом подстановки.Два правила подстановки: Независимую переменную заменяют по формуле x = t(z), где t(z) – дифференцируемая функция. Тогда dx = t'(z) dz, а интеграл приводят к виду . После интегрирования получится функция независимой переменной z. Чтобы возвратиться к переменной х, надо определить z через х и подставить это значение вместо z в найденную функцию.Полагаем z = f(x), тогда f(x)dx = g(z)dz. Вычисление интеграла сводится к вычислению  . Чтобы возвратиться к переменной х, надо подставить в полученную функцию f(x) вместо z Пример 1.  задача сведена к вычислению  , гдеt = cos(x)  Пример 2. Вычислить интеграл  Делаем подстановку t=sin(x), тогда 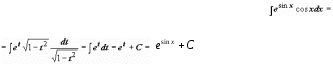  В результате  Пример 3. 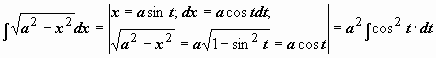 Пример 4.   Метод интегрирования по частям Пусть u=u(x) и v=v(x) функции, имеющие непрерывные производные. Тогда d(uv) = udv+ vdu. Интегрируя это равенство получим  или  Эта формула называется формулой интегрирования по частям. Интегрирование по частям состоит в том, что подинтегральное выражение заданного интеграла представляется каким-либо образом в виде произведения двух множителей u и dv. Типы интегралов, вычисляемые по частям ( Р(х) – многочлен, к – число, u = Р(х )): dv = P(x) dx  Пример 1. Найти интеграл В интегралах рассматриваемого типа за всегда обозначается логарифм Находим дифференциал du 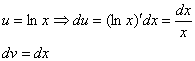 Теперь находим функцию . Для того чтобы найти функцию необходимо проинтегрировать равенства : 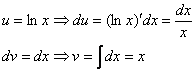 Теперь открываем наше решение и конструируем правую часть формулы: .  Пример 2. Найти интеграл Обозначим: u(x) = lnx. Тогда, если обозначить «остаток» подинтегрального выражения через dv(x): dv(x) = xdx, можно применять формулу.   ТЕМА 4. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ Основные свойства и методы вычисления Пусть на отрезке [a,b] (b>a) задана непрерывная функция y = f(x) , принимающая на этом отрезке неотрицательные значения : 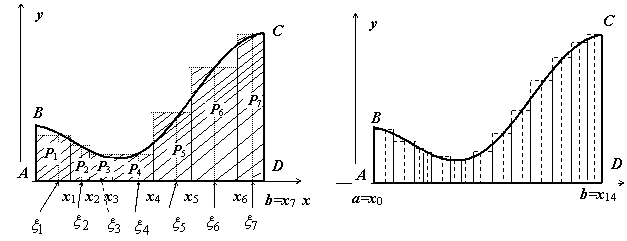 при  . Требуется определить площадь фигуры S, ограниченной снизу отрезком [a,b], слева и справа - прямыми x = a и x = b, сверху – функцией y = f(x). Эта фигура называется криволинейной трапеции ABCD  Для решения этой задачи разделим произвольным образом основание AD фигуры точками x0 = a, x1 , x2 , …, xn-1 = a, xn = b на n частей [x0 , x1], [x1 , x2], …, [xi-1 , xi], …, [xn-1 , xn]; символом 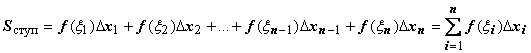 будем обозначать длину i-го отрезка:  . На каждом из отрезков [xi-1 , xi] выберем произвольную точку , найдём , вычислим произведение (это произведение равно площади прямоугольника Pi с основанием [xi-1 , xi] и высотой ) и просуммируем эти произведения по всем прямоугольникам. Полученную сумму обозначим S n  . Sn называется интегральной суммой функции y = f(x) на отрезке [a,b] Sn равно площади ступенчатой фигуры, образованной прямоугольниками Pi , i = 1,2,…,n; на левом рисунке эта площадь заштрихована. Sступ не равна искомой площади S, она только даёт некоторое приближение к S. О  бозначим через длину наибольшего частичного отрезка Если существует (конечный) предел последовательности интегральных сумм Sn при 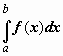 , не зависящий ни от способа разбиения отрезка [a,b] на части [xi-1 , xi], ни от выбора точек , то функция f(x) называется интегрируемой по отрезку [a,b], а этот предел называется определённым интегралом от функции f(x) по отрезку [a,b] и обозначается  . Функция f(x), как и в случае неопределённого интеграла, называется подынтегральной, числа a и b - соответственно, нижним и верхним пределами интегрирования. К  ратко определение иногда записывают так: . В этом определении предполагается, что b> a. Свойства определенного интеграла  Если b=a, то если b<a, то    6 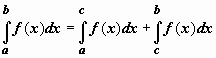 . Если функция y=f(x) интегрируема на отрезке [a,b] , то для любой точки с внутри отрезка верно равенствоИнтегрирование неравенств. Если в любой точке 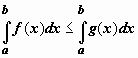выполняется неравенство  , и функции f(x), g(x) интегрируемы по отрезку [a,b], то  . Геометрический смысл определённого интеграла 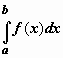 Если f(x) >0 на отрезке [a,b], то равен площади криволинейной трапеции ABCD, ограниченной снизу отрезком [a,b], слева и справа - прямыми x = a и x = b, сверху – функцией y = f(x). Вычисление определённого интеграла. Формула Ньютона-Лейбница Е 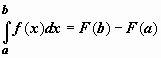 сли f(x) непрерывна на отрезке [a, b], и F(x) - некоторая первообразная функции  , то Пример 1. применения формулы Ньютона-Лейбница: 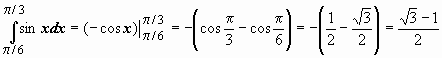 . Пример 2. Вычислить определенный интеграл Решение:  Пример 3.  Вычислить интегралы: 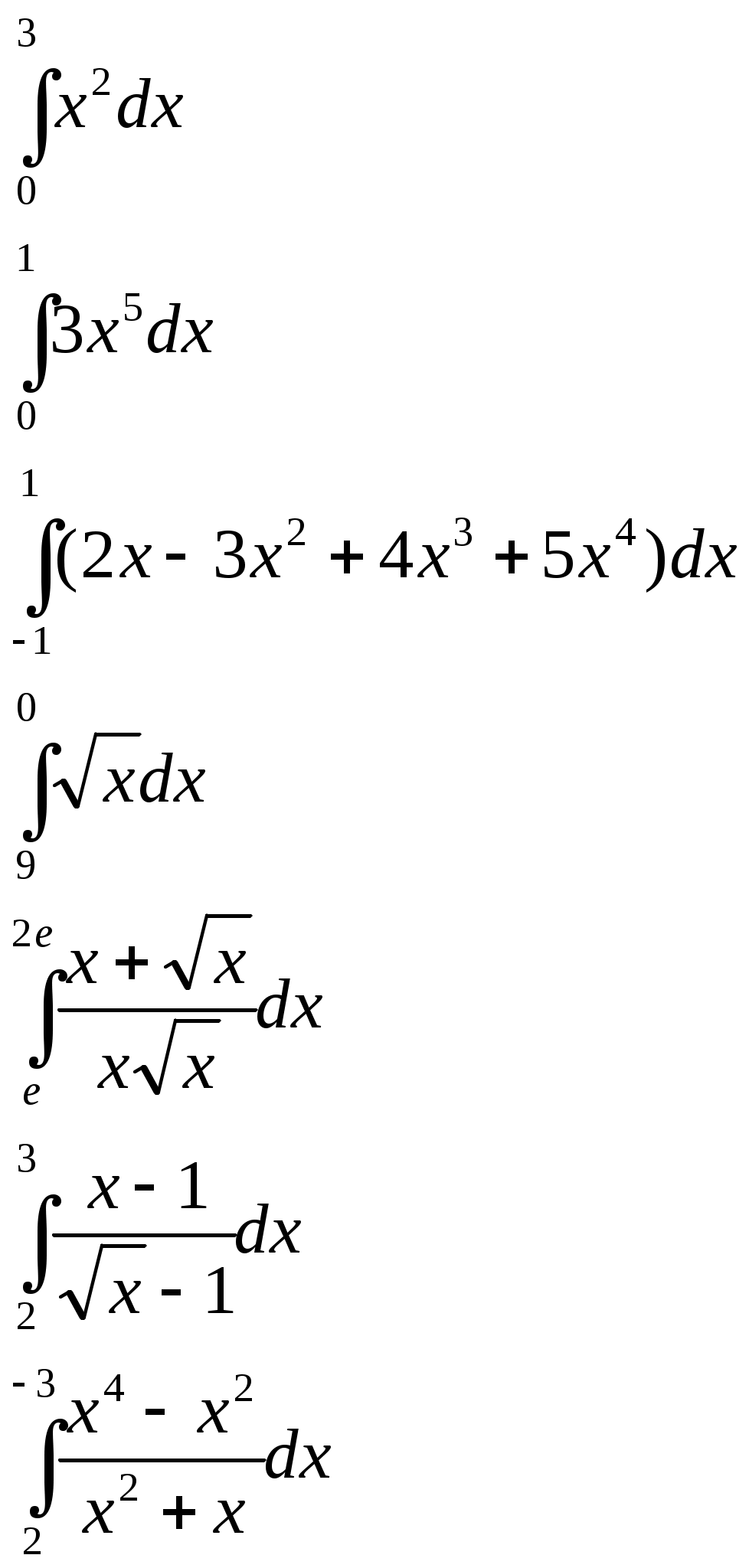 Замена переменной в определённом интеграле Теорема. Пусть функция 1.определена, непрерывно дифференцируема и монотонна на отрезке 2. ф ункция 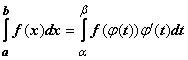непрерывна на отрезке [a, b]Т  огда Пример 4. 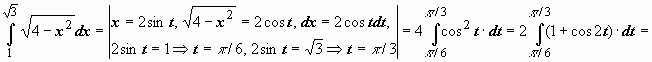 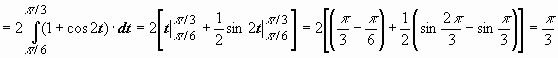 Пример Вычислить определенный интеграл Пример Вычислить определенный интеграл Вычисление площадей плоских фигур Пример 1. Найти площадь фигуры, ограниченной линиями 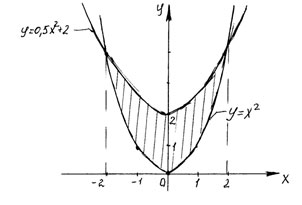 ,  . Рисунок 2 Решение:  – парабола, вершина (m,n). (0;2) – вершина
Найдём пределы интегрирования. 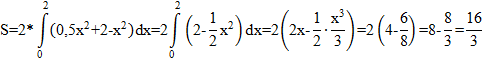    Ответ:  (кв.ед).Пример 2. Вычислить площадь фигуры, ограниченной линиями , , , . Выполним чертеж (уравнение задает ось ): 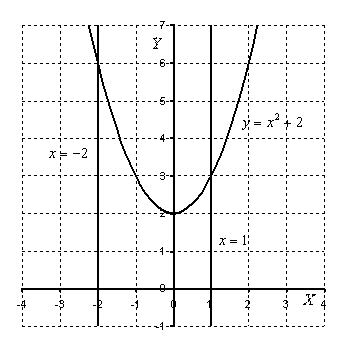 На отрезке график функции расположен над осью , поэтому: 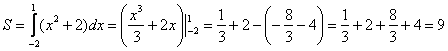 Ответ: Пример 3. Вычислить площадь фигуры, ограниченной линиями a) f( x ) = 2 х – х 2 и осью абсцисс Решение: График функции f(x) = 2x - х2 парабола. Вершина: (1; 1). 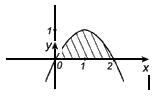  Ответ: Пример 4. Найти площадь фигуры, ограниченной линиями Решение: График функции – прямая.
Функция является обратной функции y = х 2 на промежутке [0; +∞).
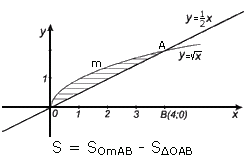 Пределы интегрирования указаны в таблицах значений функций. 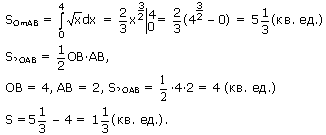 Ответ: ( кв . ед ) |