|
|
Лекции 2 курс СПО математика 48 часов. лекции 2 курс. Методическое пособие по дисциплине математика г. Балахна 2021г Данное методическое пособие предназначено для студентов, обучающихся по специальностям
Пусть функция определена в точке и некоторой ее окрестности. Придадим аргументу приращение такое, что точка попадает в область определения функции. Функция при этом получит приращение 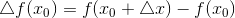 . .
Производной функции в точке называется предел отношения приращения функции в этой точке к приращению аргумента , при (если этот предел существует и конечен), т.е.
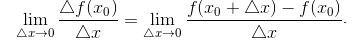
Обозначают: 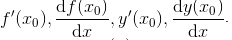
Производной функции в точке справа (слева) называется
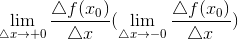
(если этот предел существует и конечен).
Обозначают: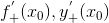 – производная y=f(x) в точке справа, – производная y=f(x) в точке справа,
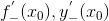 – производная y=f(x) в точке слева. – производная y=f(x) в точке слева.
Теорема: Функция y=f(x) имеет производную в точке тогда и только тогда, когда в этой точке существуют и равны между собой производные функции справа и слева. Причем
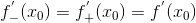 . .
Теорема (необходимое условие существования производной функции в точке). Если функция y = f(x) имеет производную в точке , то функция f(x) в этой точке непрерывна.
Физический и геометрический смысл производной
Если функция y = f(x) и ее аргумент x являются физическими величинами, то производная – скорость изменения переменной y относительно переменной x в точке . Например, если S = S(t) – расстояние, проходимое точкой за время t, то ее производная – скорость в момент времени . Если q = q(t) – количество электричества, протекающее через поперечное сечение проводника в момент времени t, то – скорость изменения количества электричества в момент времени , т.е. сила тока в момент времени .
2) Геометрический смысл производной.
Пусть – некоторая кривая, – точка на кривой .
Любая прямая, пересекающая не менее чем в двух точках называется секущей.
Касательной к кривой в точке называется предельное положение секущей если точка стремится к , двигаясь по кривой.
Рассмотрим кривую y = f(x) (т.е. график функции y = f(x)). Пусть в точке 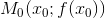 он имеет невертикальную касательную . Ее уравнение: он имеет невертикальную касательную . Ее уравнение: 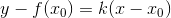 (уравнение прямой, проходящей через точку (уравнение прямой, проходящей через точку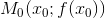 и имеющую угловой коэффициент k). и имеющую угловой коэффициент k).
По определению углового коэффициента , где – угол наклона прямой к оси .
Таким образом, – угловой коэффициент касательной к графику функции y = f(x) в точке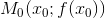 - геометрический смысл производной функции в точке - геометрический смысл производной функции в точке
Поэтому уравнение касательной к кривой y = f(x) в точке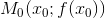 можно записать в виде можно записать в виде
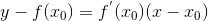
Правила дифференцирования
Пусть функции и имеют производные в точке , то справедливы следующие правила дифференцирования:
1) Производная константы равна нулю, т.е , где C – константа.
2) Производная суммы (разности) равна сумме (разности) производных, т.е 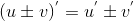 . . . .
3) Производная произведения находится по правилу: 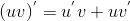 . .
4) Константу можно выносить за знак производной
, где - константа.
5) Производная дроби находится по правилу: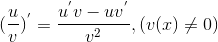 . .
6) Пусть функция y = f(x) имеет производную в точке , причем 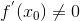 . Если существует обратная функция , то она имеет производную в точке и . Если существует обратная функция , то она имеет производную в точке и 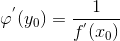 (производная обратной функции). (производная обратной функции).
Таблица производных
На основе определения производной и правил дифференцирования можно составить список табличных производных основных элементарных функций.
1. (u)' = u1 u' ( принадлежит R1 )
2. (au)' = au lna u'.
3. (eu)' = eu u'.
4. (loga u)' = u'/(u ln a).
5. (ln u)' = u'/u.
6. (sin u)' = cos u u'.
7. (cos u)' = - sin u u'.
8. (tg u)' = 1/ cos2u u'.
9. (ctg u)' = - u' / sin2u.
10. (arcsin u)' = u' / .
11. (arccos u)' = - u' / .
12. (arctg u)' = u'/(1 + u2).
13. (arcctg u)' = - u'/(1 + u2).
Пример 1
Найти производную функции y = x2 − 5x.
Решение.
Применяя линейные правила дифференцирования, получаем:
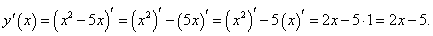
Пример 2
Найти производную функции , где a и b - константы.
Решение.
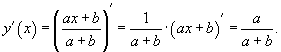
Пример 3
Найти производную функции 2√x − 3sin x.
Решение.
Используя простейшие правила дифференцирования, получаем:
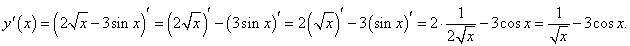
Пример 4
Найти производную функции y = 3sin x + 2cos x.
Решение.
Данное выражение представляет собой линейную комбинацию двух тригонометрических функций. Производная имеет следующий вид:
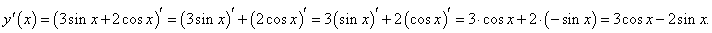
Пример 5
Найти производную функции
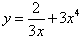
Решение
Применяя линейные свойства производной, получаем следующий ответ:
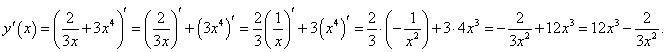
П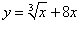 ример 6 Найти производную функции ример 6 Найти производную функции
Решение
Используя приведенные выше формулы дифференцирования, имеем:
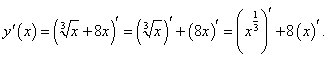
Здесь первое слагаемое является степенной функцией с показателем 1/3. Тогда для производной получаем следующее выражение:
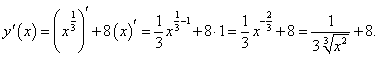
Пример 7
Вычислить производную следующей функции
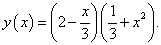
Решение
Чтобы решить данный пример с помощью рассмотренных выше правил дифференцирования, перемножим обе скобки и запишем функцию в таком виде:
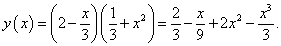
Теперь легко найти производную:
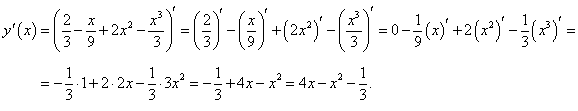
Пример 8 Найти производную функции 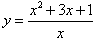 , не используя формулу производной частного. , не используя формулу производной частного.
Решение
Разделив числитель на знаменатель почленно, запишем функцию в виде
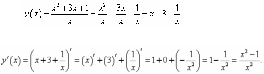
Далее, применяя линейные свойства производной, находим:
Производная сложной функции
Если функция имеет производную в точке , а функция имеет производную в точке , то сложная функция 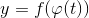 имеет производную в точке , причем имеет производную в точке , причем 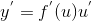 (правило дифференцирования сложной функции). (правило дифференцирования сложной функции).
Пример 9. Найти производную сложной функции y= .
Решение.
Представим функцию y= в виде двух функций: y = eu и u = x2. Имеем: y'x =y 'u u'x = (eu)'u(x2)'x = eu 2x. Подставляя x2 вместо u, получим y=2x
Пример 10. Найти производную сложной функции y=ln sin x.
Решение.
Обозначим u=sin x, тогда производная сложной функции y = lnu
вычисляется по формуле
y' = (ln u)'u(sin x)'x=
Пример11. Найти производную сложной функции y= , u=x4 +1.
Решение.
По правилу дифференцирования сложной функции, получим:
y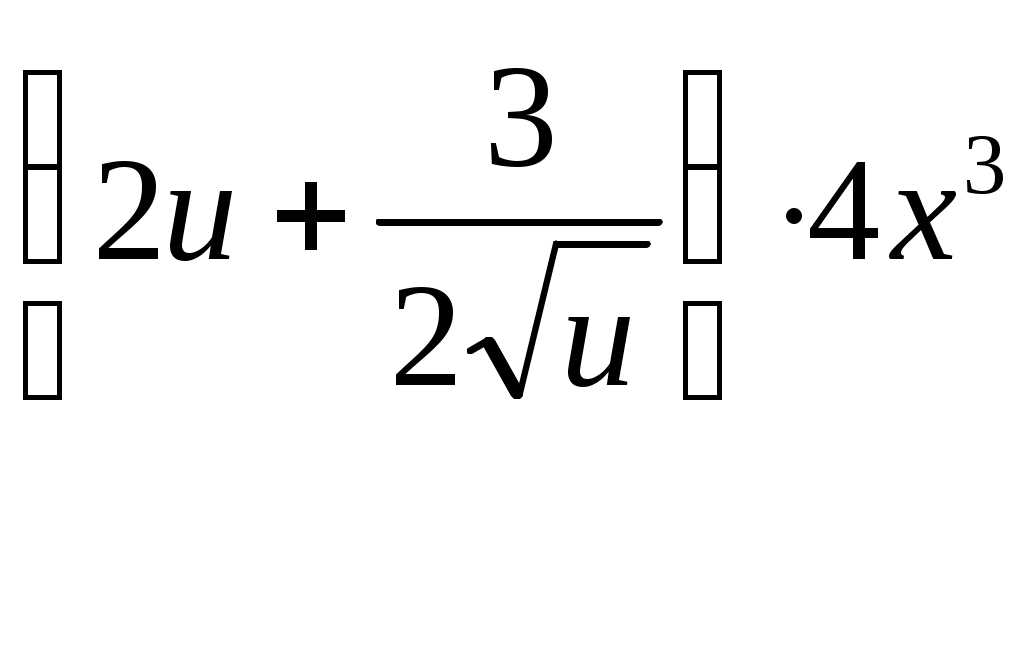 'x =y 'u u'x =( )'u(x4 +1)'x = 'x =y 'u u'x =( )'u(x4 +1)'x =
Т ак как u=x4+1, то y'x= ак как u=x4+1, то y'x=
Дифференциал и его геометрический смысл
Пусть функция у=ƒ(х) имеет в точке х отличную от нуля производную.
 , тогда , тогда
Дифференциал функции у=ƒ(х) в точке х равен произведению ее производной на дифференциал аргумента:
dy= ƒ'(х)dx
Дифференциалом аргумента называется приращение аргумента: dx = ∆х
Дифференциал dу называют также дифференциалом первого порядка.
Из формулы следует равенство dy/dx=ƒ'(х).
С геометрической точки зрения дифференциал функции в точке х представляет собой приращение ординаты касательной к графику функции в этой точке, когда х получит приращение ∆х. При малых ∆х величина приращения функции ∆у приближенно равна дифференциалу: ∆у = dy
Основные свойства дифференциала
Пусть u=u(x) и v=v(x) дифференцируемые функции, тогда
dC = 0, гдеС = const;
d(Cu) =C du
d(u + v) = du + dv
d(uv)= udv + vdu
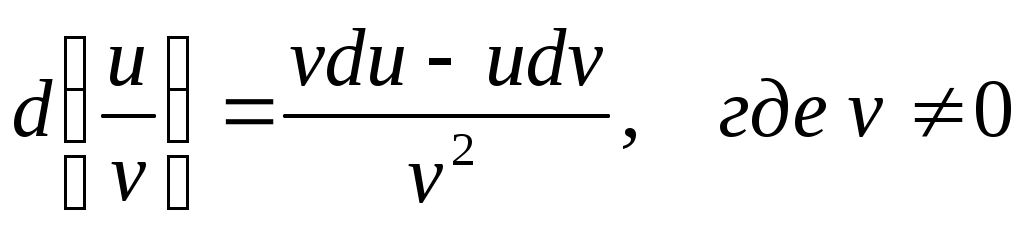
d(f(u))=ƒ'(u)du
Применение дифференциала к приближенным вычислениям
Пример 1: Найти дифференциал функции y=cos(x)
dy = (cos x)’dx, dy = - sinx dx
Пример 2: Найти дифференциал функции ƒ(х)=3x2-sin(l+2x).
Решение: По формуле dy=ƒ'(х) dx находим
dy=(3х2-sin(l+2x))'dx = (6х - 2cos(l+2х))dx.
Пример 3: Найти дифференциал функции y = 2,5x4 – 7,5x2 + 8 и вычислить насколько изменится значение функции при изменении ее аргумента от х = 2 до х = 2,003
Решение:
∆у ≈dy=y'dx=(10x3 – 15x) ∆х = (10*8 – 15*2)*0.003 =50*0.003 = 0.15
∆у≈0.15
Пример 4: Дана функция f(x) = 2x3 – 6x2 + 4x - 1
Найти (приближенно) значение F(1,005)
Решение:
Пусть х= 1 и ∆х = 0,005, тогда
F(x + ∆х) = F(1,005) = F(x) + ∆F(х) = F(1) + ∆F(х)
F(1) = 2*1 – 6*1 + 4*1 – 1 = – 1
∆F(х) ≈ dF(x) = F'(х) dx = (6x2 – 12x + 4) ∆x = (6*1 – 12*1 + 4) * 0,005 = -0,01
F(1,005) = -1 + (-0,01) = - 1,01

Пример 5: Найти приближенное значение приращения функции у=х3-2х+1 при х=2 и ∆х=0,001.

Решение: Применяем формулу ∆у≈dy=(х3-2х+1)'•∆х=(3х2-2)•∆х.
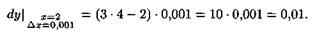
Итак, ∆у≈ 0,01.
Посмотрим, какую погрешность допустили, вычислив дифференциал функции вместо ее приращения. Для этого найдем ∆у:
∆у=((х+∆х)3-2(х+∆х)+1)-(х3-2х+1)=х3+3х2•∆х+3х•(∆х)2+(∆х)3-2х-2•∆х+1-х3+2х-1=∆х(3х2+3х•∆х+(∆х)2-2);
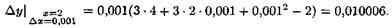
Абсолютная погрешность приближения равна
|∆у-dy|=|0,010006-0,011=0,000006.
Подставляя значения ∆у и dy, получим
ƒ(х+∆х)-ƒ(х)≈ƒ'(х)∆х
или
ƒ(х+∆х)≈ƒ(х)+ƒ'(х)•∆х.
Формула используется для вычислений приближенных значений функций.

Пример 6:
Вычислить приближенно arctg(1,05).

Решение: Рассмотрим функцию ƒ(х)=arctgx. По формуле :
F(x + ∆х) = F(x) + ∆F(х)
arctg(x+∆х)≈arctgx+(arctgx)'•∆х,
т. е.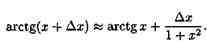
Так как х+∆х=1,05, то при х=1 и ∆х=0,05 получаем:
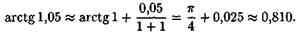

Таблица дифференциалов
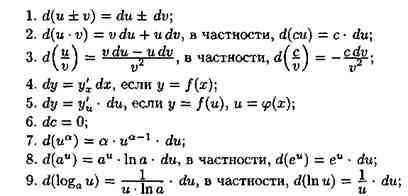 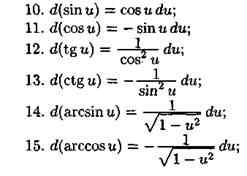 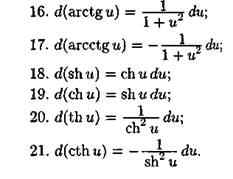
Производные высших порядков
Определение: Пусть F’(x) – производная от функции F(x) , тогда производная от функции F’(x) называется второй производной от функции F(x) и обозначается F”(x).
Физический смысл: Если функция у = F(x) описывает закон движения материальной точки по прямой, то первая производная F’(x) – мгновенная скорость точки в момент времени, а вторая производная равна скорости изменения функции, т.е. ускорению движущейся точки в этот момент времени.
Итак, у"=(у')'.
Производная от производной второго порядка, если она существует, называется производной третьего порядка и обозначается у'" (или ƒ'"(х)).
Итак, у'"=(y")'
Производной n-го порядка (или n-й производной) называется производная от производной (n-1) порядка:
y(n)=(y(n-1))' .
Производные порядка выше первого называются производными высших порядков.
Начиная с производной четвертого порядка, производные обозначают римскими цифрами или числами в скобках (уV или у(5)— производная пятого порядка). |
|
|
 Скачать 1.81 Mb.
Скачать 1.81 Mb.
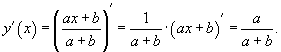
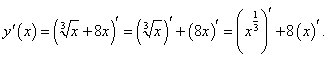
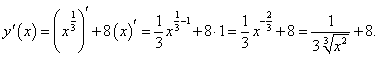
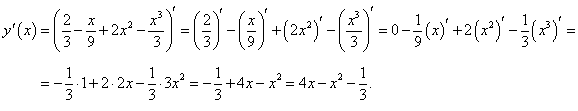
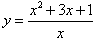 , не используя формулу производной частного.
, не используя формулу производной частного. 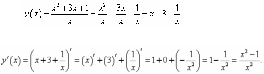
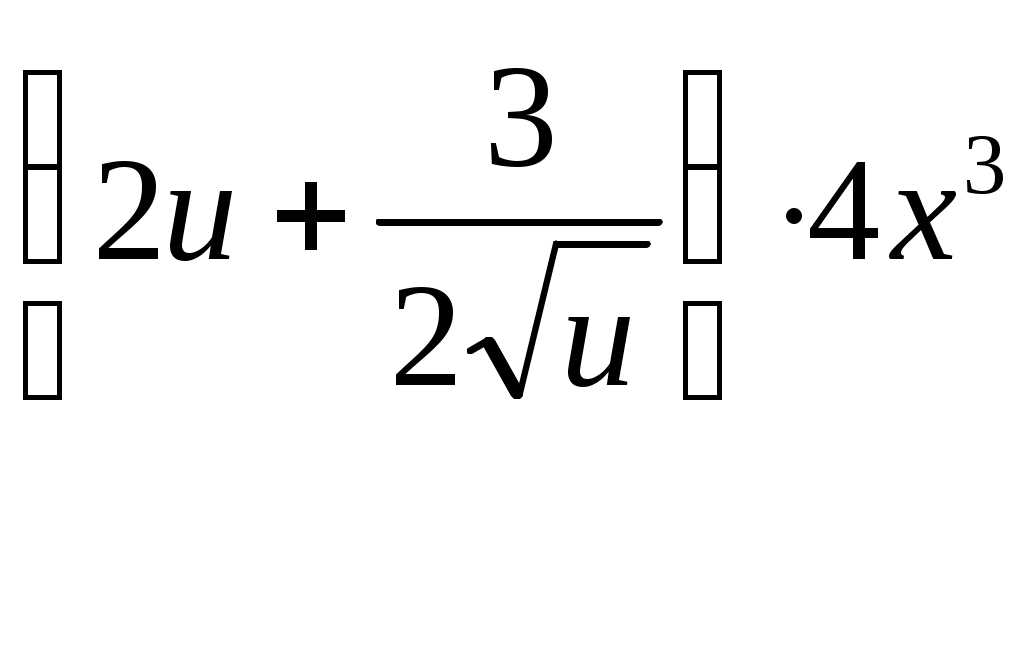 'x =y 'u u'x =( )'u(x4 +1)'x =
'x =y 'u u'x =( )'u(x4 +1)'x =