Лекции 2 курс СПО математика 48 часов. лекции 2 курс. Методическое пособие по дисциплине математика г. Балахна 2021г Данное методическое пособие предназначено для студентов, обучающихся по специальностям

• Название: Методическое пособие по дисциплине математика г. Балахна 2021г Данное методическое пособие предназначено для студентов, обучающихся по специальностям
• Анкор: Лекции 2 курс СПО математика 48 часов
• Дата: 11.02.2022
• Размер: 1.81 Mb.
• Имя файла: лекции 2 курс.doc
• Тип: Методическое пособие; #358225
• страница: 8 из 8

ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ

Задачи математической статистики

Установление закономерностей, которым подчинены массовые случайные явления, основано на изучении методами теории вероятностей статистических данных - результатов наблюдений.

Статистические данные представляют собой данные, полученные в результате обследования большого числа объектов или явлений; следовательно, математическая статистика имеет дело с массовыми явлениями.

Первая задача математической статистики - указать способы сбора и группировки статистических сведений, полученных в результате наблюдений или в результате специально поставленных экспериментов.

Вторая задача математической статистики - разработать методы анализа статистических данных в зависимости от целей исследования.

Современная математическая статистика разрабатывает способы определения числа необходимых испытаний до начала исследования, в ходе исследования и решает многие другие задачи. Современную математическую статистику определяют как науку о принятии решений в условиях неопределенности

Итак, задача математической статистики состоит в создании методов сбора и обработки статистических данных для получения научных и практических выводов.

Генеральная и выборочная совокупность статистических данных

Пусть требуется изучить совокупность однородных объектов относительно некоторого качественного или количественного признака, характеризующего эти объекты.

Качественными признаками объект обладает либо не обладает. Они не поддаются непосредственному измерению (например, спортивная специализация, квалификация, национальность, территориальная принадлежность и т. п.).

Количественные признаки представляют собой результаты подсчета или измерения. В соответствии с этим они делятся на дискретные и непрерывные.

Иногда проводиться сплошное обследование, т.е. обследуют каждый из объектов совокупности относительно признака, которым интересуются. На практике сплошное обследование применяют сравнительно редко. Например, если совокупность содержит очень большое число объектов, то провести сплошное обследование физически невозможно. В таких случаях случайно отбирают из всей совокупности ограниченное число объектов и подвергают их изучению.

Различают генеральную и выборочную совокупности.

Выборочной совокупностью (выборкой) называют совокупность случайно отобранных объектов.

Генеральной (основной) совокупностью называют совокупность, объектов из которых производится выборка.

Объемом совокупности (выборочной или генеральной) называют число объектов этой совокупности. Например, если из 1000 деталей отобрано для обследования 100 деталей, то объем генеральной совокупности N = 1000, а объем выборки n =100. Число объектов генеральной совокупности N значительно превосходит объем выборки n .

Способы выборки

При составлении выборки можно поступать двумя способами: после того как объект отобран и над ним произведено наблюдение, он может быть возвращен либо не возвращен в генеральную совокупность. В соответствии со сказанным выборки подразделяют на повторные и бесповторные.

Повторной называют выборку, при которой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность.

Бесповторной называют выборку, при которой отобранный объект в генеральную совокупность не возвращается.

На практике обычно пользуются бесповторным случайным отбором.

Для того чтобы по данным выборки можно было достаточно уверенно судить об интересующем признаке генеральной совокупности, необходимо, чтобы объекты выборки правильно его представляли (выборка должна правильно представлять пропорции генеральной совокупности) - выборка должна быть репрезентативной (представительной).

Выборка будет репрезентативной, если:

• 
  каждый объект выборки отобран случайно из генеральной совокупности;
  
• 
  все объекты имеют одинаковую вероятность попасть в выборку.
  

Дискретный вариационный ряд

Обычно полученные наблюдаемые данные представляют собой множество расположенных в беспорядке чисел. Просматривая это множество чисел, трудно выявить какую-либо закономерность их варьирования (изменения). Для изучения закономерностей варьирования значений случайной величины опытные данные подвергают обработке.

Пример. Проводились наблюдения над числом Х оценок полученных студентами ВУЗа на экзаменах. Наблюдения в течение часа дали следующие результаты: 3; 4; 3; 5; 4; 2; 2; 4; 4; 3; 5; 2; 4; 5; 4; 3; 4; 3; 3; 4; 4; 2; 2; 5; 5; 4; 5; 2; 3; 4; 4; 3; 4; 5; 2; 5; 5; 4; 3; 3; 4; 2; 4; 4; 5; 4; 3; 5; 3; 5; 4; 4; 5; 4; 4; 5; 4; 5; 5; 5. Здесь число Х является дискретной случайной величиной, а полученные о ней сведения представляют собой статистические (наблюдаемые) данные.

Расположив приведенные выше данные в порядке неубывания и сгруппировав их так, что в каждой отдельной группе значения случайной величины будут одинаковы, получают ранжированный ряд данных наблюдения.

В примере 1 имеем четыре группы со следующими значениями случайной величины: 2; 3; 4; 5. Значение случайной величины, соответствующее отдельной группе сгруппированного ряда наблюдаемых данных, называют вариантом, а изменение этого значения варьированием.

Варианты обозначают малыми буквами латинского алфавита с соответствующими порядковому номеру группы индексами - x_i. Число, которое показывает, сколько раз встречается соответствующий вариант в ряде наблюдений называют частотой варианта и обозначают соответственно - n_i.

Сумма всех частот ряда   - объем выборки. Отношение частоты варианта к объему выборки n_i/ n = w_i называют относительной частотой.

Статистическим распределением выборки называют перечень вариантов и соответствующих им частот или относительных частот (табл. 1, табл. 2).

Пример 2. Задано распределение частот выборки объема n = 20: 

Таблица 1

xi	2	6	12
ni	3	10	7

Написать распределение относительных частот.

Решение. Найдем относительные частоты, для чего разделим частоты на объем выборки:

W₁ = 3/20 = 0,15; W₂ = 10/20 = 0,50; W₃ = 7/20 = 0,35.

Напишем распределение относительных частот: 

Таблица 2

xi	2	6	12
wi	0,15	0,50	0,35

Контроль: 0,15 + 0,50 + 0, 35 = 1.

Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот (в качестве частоты, соответствующей интервалу, принимают сумму частот, попавших в этот интервал).

Дискретным вариационным рядом распределения называют ранжированную совокупность вариантов x_i с соответствующими им частотами n_i или относительными частотами w_i.

Для рассмотренного выше примера 1 дискретный вариационный ряд имеет вид: 

Таблица 3

xi	2	3	4	5
ni	8	12	23	17
wi	8/60	12/60	23/60	17/60

Контроль: сумма всех частот вариационного ряда (сумма значений второй строки таблицы 3) есть объем выборки (в примере 1 n = 60); сумма относительных частот вариационного ряда должна быть равна 1 (сумма значений третьей строки таблицы 3)

Интервальный вариационный ряд

Если изучаемая случайная величина является непрерывной, то ранжирование и группировка наблюдаемых значений зачастую не позволяют выделить характерные черты варьирования ее значений. Это объясняется тем, что отдельные значения случайной величины могут как угодно мало отличаться друг от друга и поэтому в совокупности наблюдаемых данных одинаковые значения величины могут встречаться редко, а частоты вариантов мало отличаются друг от друга.

Нецелесообразно также построение дискретного ряда для дискретной случайной величины, число возможных значений которой велико. В подобных случаях следует строить интервальный вариационный ряд распределения.

Для построения такого ряда весь интервал варьирования наблюдаемых значений случайной величины разбивают на ряд частичных интервалов и подсчитывают частоту попадания значений величины в каждый частичный интервал.

Интервальным вариационным рядом называют упорядоченную совокупность интервалов варьирования значений случайной величины с соответствующими частотами или относительными частотами попаданий в каждый из них значений величины.

Для построения интервального ряда необходимо:

1. 
   определить величину частичных интервалов;
   
2. 
   определить ширину интервалов;
   
3. 
   установить для каждого интервала его верхнюю и нижнюю границы;
   
4. 
   сгруппировать результаты наблюдении.
   

1. Вопрос о выборе числа и ширины интервалов группировки приходится решать в каждом конкретном случае исходя из целей исследования, объема выборки и степени варьирования признака в выборке.

Приблизительно число интервалов k можно оценить исходя только из объема выборки n одним из следующих способов:

• 
  по формуле Стержеса: k = 1 + 3,32·lg n;
  
• 
  с помощью таблицы 1.
  

Таблица 1

Объем выборки, n	25-40	40-60	60-100	100-200	Больше 200
Число интервалов, k	5-6	6-8	7-10	8-12	10-15

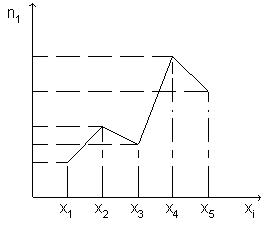
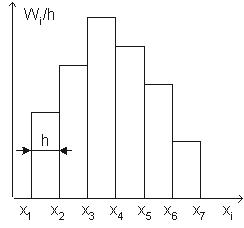
2. Обычно предпочтительны интервалы одинаковой ширины. Для определения ширины интервалов h вычисляют:

• 
  размах варьирования R - значений выборки: R = x_max- x_min,
  

где x_max и x_min - максимальная и минимальная варианты выборки;

• 
  ширину каждого из интервалов h определяют по следующей формуле: h = R/k.
  

3. Нижняя граница первого интервала x_h1 выбирается так, чтобы минимальная варианта выборки x_min попадала примерно в середину этого интервала: x_h1= x_min- 0,5·h.

Промежуточные интервалы получают прибавляя к концу предыдущего интервала длину частичного интервала h:

x_hi= x_hi-1+h.

Построение шкалы интервалов на основе вычисления границ интервалов продолжается до тех пор, пока величина x_hi удовлетворяет соотношению:

x_hi< x_max+ 0,5·h.

4. В соответствии со шкалой интервалов производится группирование значений признака - для каждого частичного интервала вычисляется сумма частот n_i вариант, попавших в i-й интервал. При этом в интервал включают значения случайной величины, большие или равные нижней границе и меньшие верхней границы интервала.

Полигон и гистограмма

Для наглядности строят различные графики статистического распределения.

По данным дискретного вариационного ряда строят полигон частот или относительных частот.

Полигоном частот называют ломанную, отрезки которой соединяют точки (x₁; n₁), (x₂; n₂), ..., (x_k; n_k). Для построения полигона частот на оси абсцисс откладывают варианты x_i, а на оси ординат - соответствующие им частоты n_i. Точки ( x_i; n_i) соединяют отрезками прямых и получают полигон частот (Рис. 1).

Полигоном относительных частот называют ломанную, отрезки которой соединяют точки (x₁; W₁), (x₂; W₂), ..., (x_k; W_k). Для построения полигона относительных частот на оси абсцисс откладывают варианты x_i, а на оси ординат - соответствующие им относительные частоты W_i. Точки ( x_i; W_i) соединяют отрезками прямых и получают полигон относительных частот.

В случае непрерывного признака целесообразно строить гистограмму.

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношению n_i/ h (плотность частоты).

Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии n_i/ h.

Площадь i - го частичного прямоугольника равна hn_i/ h = n_i - сумме частот вариант i - го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, т.е. объему выборки.

Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношению W_i/ h (плотность относительной частоты).

Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии W_i/ h (Рис. 2).

Площадь i - го частичного прямоугольника равна hW_i/ h = W_i - относительной частоте вариант попавших в i -й интервал. Следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. единице. 

Рис. 1. Полигон частот

Рис. 2. Гистограмма относительных частот

 

Оценка параметров генеральной совокупности
Характеристики положения

Основными параметрами генеральной совокупности являются математическое ожидание (генеральная средняя) М(Х) и среднее квадратическое отклонение . Это постоянные величины, которые можно оценить по выборочным данным. Оценка генерального параметра, выражаемая одним числом, называется точечной.

Точечной оценкой генеральной средней является выборочное среднее  .

Выборочным средним называется среднее арифметическое значение признака выборочной совокупности.

Если все значения x₁, x₂,..., x_n признака выборки различны (или если данные не сгруппированы), то: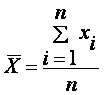



Если же все значения признака x₁, x₂,..., x_n имеют соответственно частоты n₁, n₂,..., n_k, причем n₁+ n₂+...+ n_k= n (или если выборочное среднее вычисляется по вариационному ряду), то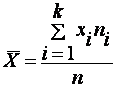



В том случае, когда статистические данные представлены в виде интервального вариационного ряда, при вычислении выборочного среднего   значениями вариант считают середины интервалов.

Выборочное среднее является основной характеристикой положения, показывает центр распределения совокупности, позволяет охарактеризовать исследуемую совокупность одним числом, проследить тенденцию развития, сравнить различные совокупности (выборочное среднее является той точкой, сумма отклонений наблюдений от которой равна 0).

Для оценки степени разброса (отклонения) какого-то показателя от его среднего значения, наряду с максимальным и минимальным значениями, используются понятия дисперсии и стандартного отклонения.

Дисперсия выборки или выборочная дисперсия (от английского variance) – это мера изменчивости переменной. Термин впервые введен Фишером в 1918 году.

Выборочной дисперсией D_в называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения  .

Если все значения x₁, x₂,..., x_n признака выборки объема n различны, то: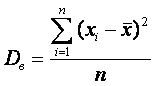



Если же все значения признака x₁, x₂,..., x_n имеют соответственно частоты n₁, n₂,..., n_k, причем n₁+ n₂+...+ n_k= n, то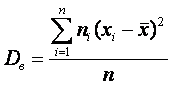



Дисперсия меняется от нуля до бесконечности. Крайнее значение 0 означает отсутствие изменчивости, когда значения переменной постоянны.

Среднее квадратическое отклонение (стандартное отклонение), (от английского standard deviation) вычисляется как корень квадратный из дисперсии.

Чем выше дисперсия или стандартное отклонение, тем сильнее разбросаны значения переменной относительно среднего.

Непараметрическими характеристиками положения являются мода и медиана.

Модой M_o называется варианта, имеющая наибольшую частоту или относительную частоту.

Медианой M_e называется варианта, которая делит вариационный ряд на две части, равные по числу вариант.

При нечетном числе вариант (n=2k+1)

M_e= x_k+1,

а при четном числе вариант (n=2k)

M_e= (x_k+ x_k+1)/2.

ИСПОЛЬЗУЕМАЯ ЛИТЕРАТУРА

1. 
   Богомолов Н. В., Самойленко П. И. Математика. – М.: издательство «Дрофа», 2009.
   
2. 
   Виноградов Ю.Н., Гомола А.И. Математика и информатика. М.: Издательский центр «Академия», 2010.
   
3. 
   Гмурман В.Е. Теория вероятностей и математическая статистика: Учебное пособие для студентов вузов. Изд. 6-е, стер.. - М.: Высш. шк., 1997.
   Ильин, В.А. Линейная алгебра и аналитическая геометрия: Учебник / В.А. Ильин, Г.Д. Ким. - М.: Проспект, 2012. - 400 c.
   
4. 
   Григорьев С. Г., Задулина С. В. Математика: учебник для студ. сред.проф. учреждений. – 3-е изд. – М.: ОИЦ «Академия», 2009.
   
5. 
   Дадаян А. А. Сборник задач по математике: учеб.пособие для ссузов. – М.: Форум: Инфра-М, 2010.
   
6. 
   Кремер Н.Ш. Высшая математика для экономистов. Учебник Москва, ЮНИТИ 2000
   
7. 
   Кремер Н.Ш. Теория вероятностей и математическая статистика для экономистов. Учебник-М.ЮНИТИ 2001 . 
   
8. 
   Лунгу, К.Н. Сборник задач по высшей математике. 1 курс: С контрольными работами: линейная алгебра; аналитическая геометрия; основы математического анализа; комплексные числа / К.Н. Лунгу, Д.Т. Письменный, С.Н. Федин, Ю.А. Шевченко. - М.: Айрис-пресс, 2011. - 576 c.