Лекции 2 курс СПО математика 48 часов. лекции 2 курс. Методическое пособие по дисциплине математика г. Балахна 2021г Данное методическое пособие предназначено для студентов, обучающихся по специальностям
 Скачать 1.81 Mb.
|
|
Министерство образования Нижегородской области Государственное бюджетное профессиональное образовательное учреждение «Балахнинский технический техникум» МЕТОДИЧЕСКОЕ ПОСОБИЕ по дисциплине МАТЕМАТИКА г.Балахна 2021г Данное методическое пособие предназначено для студентов, обучающихся по специальностям: Разработчик:
Рассмотрено на заседании Протокол № ________ от ________________ Председатель СОДЕРЖАНИЕ
ВВЕДЕНИЕ В современных условиях специалист среднего звена должен получить более широкую подготовку, чтобы иметь возможность продолжить образование и самообразование, быть востребованным на рынке труда. Это осуществимо при наличии хорошей подготовки специалиста по основополагающим дисциплинам, к которым относится и математика. Данное методическое пособие будет предназначено для студентов II курса по специальностям: Документационное обеспечение и архивоведение, Право и организация социального обеспечения, Страховое дело, Операционная деятельность в логистике, изучающих дисциплину «Математика» по учебной программе в объеме 72 часа, а также для студентов I курса по специальности «Банковское дело», изучающих дисциплину «Элементы высшей математике» в объеме 77 час. Т.к. большая часть объема учебной нагрузки студентов отведена на самостоятельную работу, то целью данного пособия является помощь студентам выработать навыки решения практических задач по математике. Пособие не заменяет учебник, но помогает как в усвоении теории, так и в приобретении навыков решения задач. Оно включает в себя основной теоретический материал и образцы решения типовых задач. Пособие будет полезно тем студентам, которые по различным причинам не смогли посетить все учебные занятия. Также оно будет полезно для подготовки к практическим занятиям, для более успешного понимания и усвоения материала. ТЕМА 1. ПРЕДЕЛЫ И НЕПРЕРЫВНОСТЬ Предел функции в точке и на бесконечности Определение предела функции в точке. Число b называется пределом функции у=f(x) при x стремящемся к a, если для любого положительного числа можно указать такое положительной число = ( ), что для всех x, отличных от a и удовлетворяющих неравенству |x-a|<, имеет место неравенство |f(x)-b|< Обозначение предела. Если b есть предел функции f(x) при x стремящемся к a, то записывают это так: Предел функции на бесконечности. Пусть задана функция у = f(x) с неограниченной сверху областью определения. Число b называется пределом данной функции при х, стремящемся к плюс бесконечности, если для любого числа существует такое положительное число М, что при всех значениях аргумента х из области определения, таких, что x > M, выполняется неравенство |f(x) – b| < . Запись этого факта:  Если область определения данной функции неограниченна снизу, то число b называется пределом данной функции при х, стремящемся к минус бесконечности, если для любого числа < 0 существует такое положительное число М, что при всех значениях аргумента х из области определения, таких, что x < –M, выполняется неравенство |f(x) – b| < . Записывается это так:  Геометрический смысл равенства состоит в следующем: прямая у = b является горизонтальной асимптотой графика функции у = f(х) (и в положительном, и в отрицательном направлении). Теоремы о пределах ТЕОРЕМА 1. Предел суммы двух функций при x стремящемся к a равен сумме пределов этих функций, то есть Т 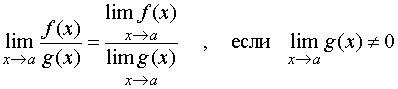 ЕОРЕМА 2. Предел произведения двух функций при x стремящемся к a равен произведению пределов этих функций, то есть Т  ЕОРЕМА 3. Предел частного двух функций при x стремящемся к a равен частному пределов, если предел знаменателя отличен от нуля, то есть  и равен плюс (минус) бесконечности, если предел знаменателя 0, а предел числителя конечен и отличен от нуля ТЕОРЕМА 4. Предел постоянной величины равен самой постоянной величине: ТЕОРЕМА 5. Постоянный коэффициент можно выносить за знак предела:   Замечательные пределы Первый замечательный предел равен Второй замечательный равен Вычисление пределов функции, раскрытие неопределенностей Пример 1. Найти предел  Пример 2. Найти предел 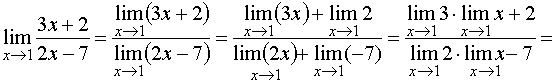 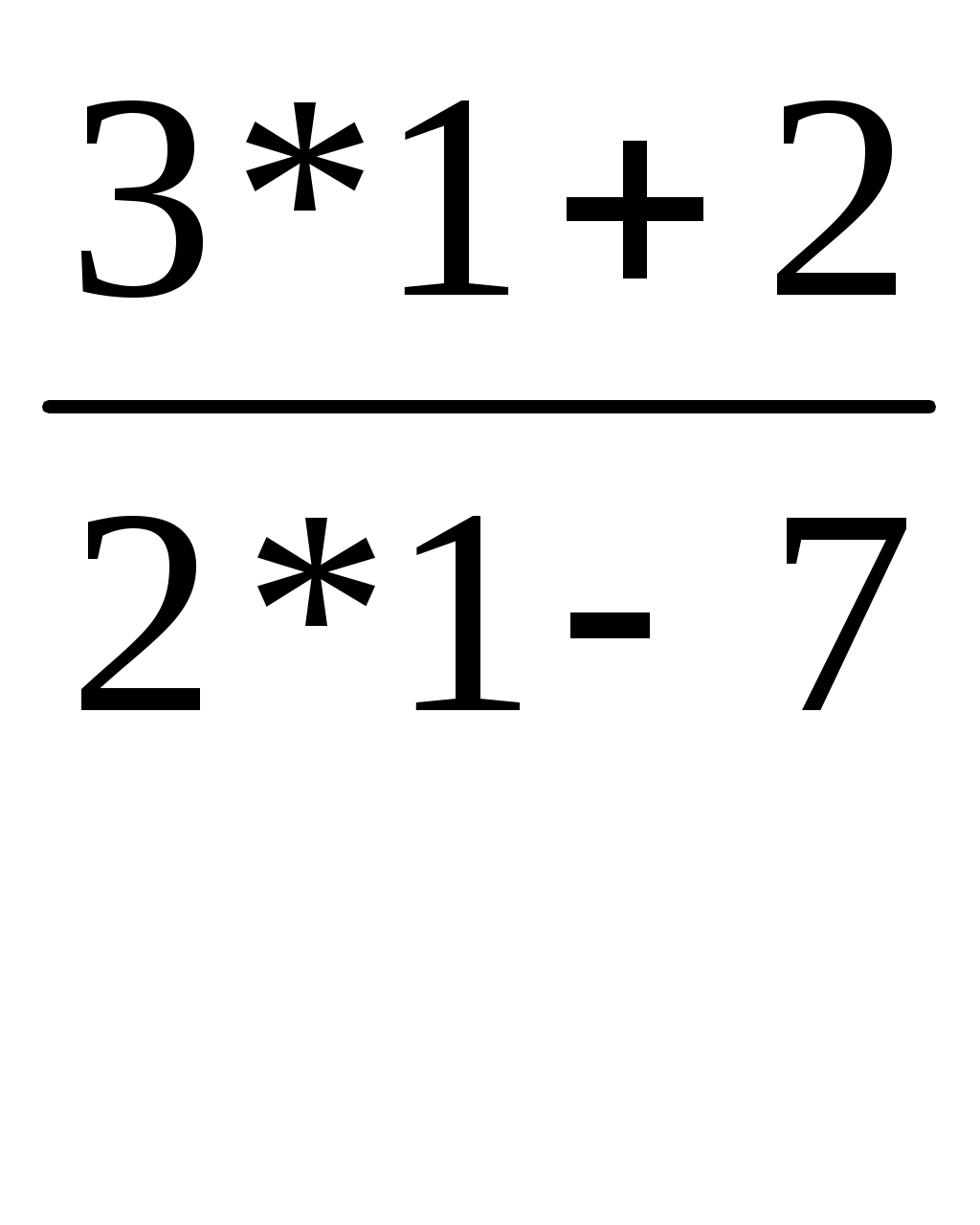 Пример 3. Найти предел Это преобразование справедливо при всех значениях x, отличных от 2, поэтому в соответствии с определением предела можем написать 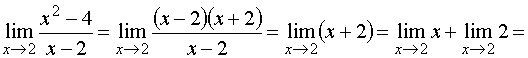  Вычисление пределов с помощью теоремы о первом замечательном пределе Пример. Найти предел 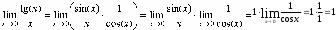 Вычисление пределов с помощью теоремы о втором замечательном пределе П 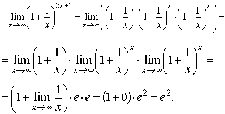 ример. Найти предел Комментарий. Вначале мы разложили выражение под пределом на множители, после применили теорему о пределе произведения. Пределы второго и третьего сомножителей равны e. Для нахождения предела первого сомножителя используем теорему о пределе суммы. Наконец, предел 1/x при x стремящемся к бесконечности равен 0, так как числитель дроби ограничен, а знаменатель неограниченно возрастает. Раскрытие неопределенности 1. Пределы с неопределенностью Правило: для того, чтобы раскрыть неопределенность необходимо разделить числитель и знаменатель на в старшей степени (т.е.на х2) Пример 1. Вычислить предел Согласно нашему правилу попытаемся подставить бесконечность в функцию. Что у нас получается вверху? Бесконечность. А что получается внизу? Тоже бесконечность. Таким образом, у нас есть так называемая неопределенность вида . Как решать пределы данного типа? Необходимо разделить числитель и знаменатель на х2 Пример 2. Вычислить предел З  десь неопределенность вида . Разделить числитель и знаменатель на Пример 3. Вычислить предел Здесь неопределенность вида . Разделить числитель и знаменатель на Ответ=2/0=0 2. Пределы с неопределенностью вида Правило: если в числителе и знаменателе находятся многочлены, и имеется неопределенность вида , то для ее раскрытия нужно разложить числитель и знаменатель на множители. Пример 4. Вычислить предел Решение Сначала попробуем подставить -1 в дробь: Получена неопределенность . Разложить числитель на множители. Ответ -7 Пример 5. Вычислить предел 3. Пределы с неопределенностью вида Метод умножения числителя и знаменателя на сопряженное выражение Следующий тип пределов похож на предыдущий тип. Единственное, помимо многочленов, добавятся корни. Пример 6. Найти предел При подстановки в выражение х =3 получена неопределенность вида , которую нужно устранить. Освобождаемся от корней. Умножаем числитель и знаменатель на сопряженное выражение  Ответ: -3/10Пример 7. Найти предел О твет: -12 Непрерывность функции. Точки разрыва и их классификация Пусть функцияy=f(x) определена в точке х0 и в некоторой окрестности этой точки. Функция y=f(x) называется непрерывной в точке х0, если существует предел функции в этой точке и он равен значению функции в этой точке, т.е. 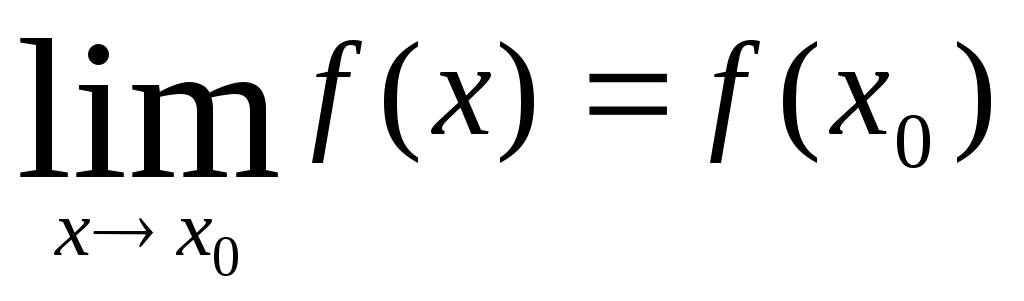 Равенство означает выполнение трех условий: функция f(x) определена в точке х0 и ее окрестности; функция f(x) имеет конечный предел при х-> х0 ; предел функции в точке х0 равен значению функции в этой точке, т.е. выполняется равенство 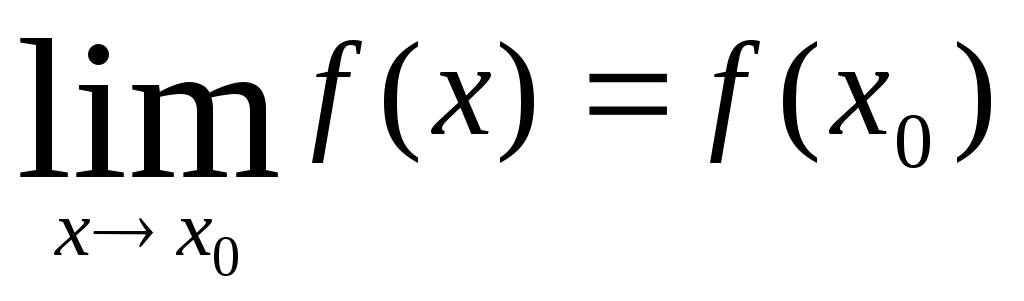Рассмотрим это определение с другой точки зрения. Пусть дана функция y=f(x), определенная в некоторой области. Если выбрать некоторое начальное значение аргумента х0 , то соответствующее значение функции f(x0) называется начальным. Если прибавить к начальному значению аргумента х0 некоторое его приращение х, то получим значение аргумента х0+ х, которому соответствует значение функции f(х0+ х). f(х0+ х)- f(x0) называется приращением функции и обозначается у. х и у могут быть как положительными, так и отрицательными числами. Если lim х=0 при х->0 , limу=0 при y->0, то приращения х и у называются бесконечно малыми. Таким образом: Если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции , то функция y=f(x) называется непрерывной в точке х0 Пример 8. Показать, что функция у= х2 непрерывна в произвольной точке х0 Решение: Возьмем приращение аргумента х т.е. рассмотрим точку х0+ х. Тогда у (х0+ х)=( х0+ х)2. у=( х0+ х)2 - х02 = х02 + 2 х0 х+( х)2 – х02 limу= lim(2 х0 х+( х)2) = 2 х0lim х + lim( х)2 =0 при х->0 т.е функция у= х2 непрерывная функция на всей числовой оси Точки разрыва функции и их классификация Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции. Если х= х0 – точка разрыва функции y=f(x) , то в ней не выполняется хотя бы одно их 3-х условий первого определения непрерывности функции. Все точки разрыва разделяются на точки разрыва первого и второго рода Точка разрыва х0 называется точкой разрыва первого рода функции y=f(x), если в этой точке существуют конечные пределы функции слева и справа (односторонние пределы), т.е. lim f(x) =A и lim f(x) = BПри этом: 1. если А=В, то точка х0 называется точкой устранимого разрыва 2. если А# В , то точка х0 называется точкой конечного разрыва Величину | A- B | называют скачком функции в точке разрыва первого рода Точки устранимого разрыва и конечного скачка называются точками разрыва 1–го рода. Их отличительным признаком является существование конечных односторонних пределов. Точка разрыва х0 называется точкой разрыва второго рода функции y=f(x), если по крайней мере один из односторонних пределов (слева или справа) не существует, или равен бесконечности Пример 9. Найти точки разрыва функции, если они существуют, б) найти односторонние пределы в точках разрыва и установить тип точек разрыва функции f(x)=2 x/(3+x) Решение: Функция f(x)=2 x/(3+x) не определена в точке х=-3, значит это точка разрыва. Найдем односторонние пределы в этой точке. Сначала найдем односторонние пределы функции lim 2x/(3+x) = - при х → -3-0 lim 2x/(3+x) = + , при х → -3+0 Один (оба) из односторонних пределов равен бесконечности, значит точка х=-3 точка разрыва второго рода. Пример 10. Найти точки разрыва функции и определить их тип f(x)= (x2 – 25)/(x-5) Решение: Область определения функции (- ,5) (5, +). Точка х = 5 – точка разрыва Рассмотрим lim f(x) при х → 5-0 Lim (x-5)(x+5)/(x -5)= lim (x+5) при х → 5 Lim (x+5) = 10 при x → 5-0 Lim (x+5) = 10 при x → 5+0 Т.е. односторонние пределы равны и х = 5 – точка устранимого разрыва 1 рода Пример 11. Исследовать функцию на непрерывность и определить вид точек разрыва У= 1/х Решение: Область определения функции (- ,0) (0, +). Точка х = 5 – точка разрыва Точка х = 0 – точка разрыва Рассмотрим односторонние пределы Lim 1/x = - при х → 0-0 Lim 1/x = + при х → 0+0 Т.е. х=0 – точка разрыва 2 рода Пример 12. Исследовать функцию на непрерывность и определить вид точек разрыва f(x) = x / (1+x2) Решение: Область определения функции (- ,-1) (-1, +). Точка х = -1 – точка разрыва Рассмотрим односторонние пределы Lim x/(1+x2) = - при х = -1-0 Lim x/(1+x2) = + при х = -1+0 Т.е. х=-1– точка разрыва 2 рода Пример 13. Исследовать функцию н а непрерывность Решение. Данная функция не определена в точках x = −1 и x = 1. Следовательно, функция имеет разрывы в точках x = ±1. Чтобы определить тип разрыва, вычислим односторонние пределы в этих точках. 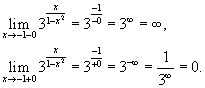 Поскольку левосторонний предел при x = −1 равен бесконечности, то данная точка является точкой разрыва второго рода. 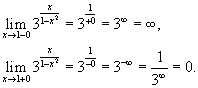 Аналогично, левосторонний предел в точке x = 1 равен бесконечности. Эта точка также является точкой разрыва второго рода. Пример 14. Показать, что функция имеет устранимый разрыв в точке x = 0. Решение: Д анная функция не определена при x = 0. Поскольку sin x является непрерывной функцией для всех x, то искомая функция также непрерывна при всех x за исключением точки x = 0. Так как то в данной точке существует устранимый разрыв. Мы можем сконструировать новую функцию 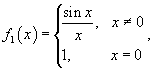 которая будет непрерывной при любом действительном x. Пример 15. Найти точки разрыва функции , если они существуют. Решение: Данная функция существует при всех значениях x, однако она состоит из двух различных функций и, поэтому, не является элементарной. Исследуем "поведение" этой функции вблизи точки x = 0, где ее аналитическое выражение изменяется. Вычислим односторонние пределы при x = 0. 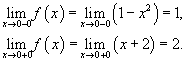 Следовательно, функция имеет точку разрыва первого рода при x = 0. Скачок функции в этой точке равен  При всех других значениях x функция является непрерывной, поскольку обе составляющие функции слева и справа от точки x = 0 представляют собой элементарные функции без точек разрыва. Пример 16. Найти точки разрыва функции , если они существуют. Решение: Данная элементарная функция определена для всех x, исключая точку x = 0, где она имеет разрыв. Найдем односторонние пределы в этой точке. 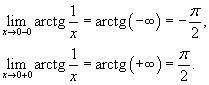 Видно, что в точке x = 0 существует разрыв первого рода ТЕМА 2. ПРОИЗВОДНАЯ. ИССЛЕДОВАНИЕ ФУНКЦИЙ С ПОМОЩЬЮ ПРОИЗВОДНОЙ |