Лекции 2 курс СПО математика 48 часов. лекции 2 курс. Методическое пособие по дисциплине математика г. Балахна 2021г Данное методическое пособие предназначено для студентов, обучающихся по специальностям
 Скачать 1.81 Mb.
|
|
ТЕМА 5. МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ Общая характеристика матрицы Матрицей размерности m*n называется таблица чисел (элементов), содержащая m строк и n столбцов. 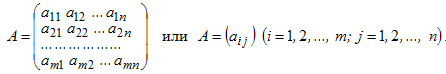 В алгебраических выражениях часто используются специального вида матрицы: Θ — нулевая D — диагональная E — единичная Если в матрице А переставить соответствующие строки и столбцы местами, то получится матрица Ат , которую называют транспонированной матрицей А. Пример: 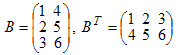 Если число строк и столбцов матрицы совпадает и равно n, то матрица называется квадратной n-го порядка.Две матрицы А и В одинаковой размерности равны, если все соответствующие элементы матриц равны. Действия над матрицами Умножение матрицы на число. Любую матрицу можно умножить на любое число, при этом все элементы матрицы умножаются на это число. Сложение матриц. Две матрицы А и В одинаковой размерности можно сложить, при этом все соответветствующие элементы матриц складываются. Свойства линейных операций 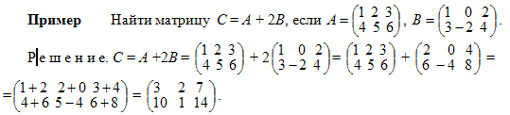      Умножение матриц Две матрицы можно умножить, если число строк второй матрицы равно числу столбцов первой матрицы. При умножении матриц получается матрица, число строк которой равно числу строк первой матрицы, а число столбцов равно числу столбцов второй матрицы. Элементы матрицы произведения С = АВ находятся по формуле: 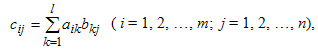 где l — число строк второй и число столбцов первой матриц. Свойства умножения матриц: 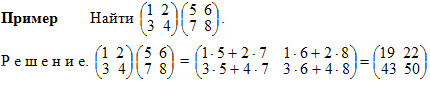   (где Е — единичная матрица)  Пример. Произведите умножение матриц  Всегда: строки первой матрицы умножаются на столбцы второй матрицы, то есть никогда не будет ситуации когда необходимо будет умножать столбцы первой на строки второй! Важно: матрицы при умножении нельзя менять местами!!! — результат умножения будет другим Обратная матрица
Пусть имеется квадратная матрица n-го порядка 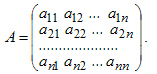 Матрица А-1 называется обратной матрицей по отношению к матрице А, если А*А-1 = Е, где Е — единичная матрица n-го порядка. Единичная матрица — такая квадратная матрица, у которой все элементы по главной диагонали, проходящей от левого верхнего угла к правому нижнему углу, — единицы, а остальные — нули, например: 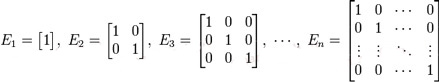 Обратная матрица может существовать только для квадратных матриц т.е. для тех матриц, у которых число строк и столбцов совпадают. Теорема условия существования обратной матрицы Для того чтобы матрица имела обратную матрицу необходимо и достаточно, чтобы она была невырожденной. Матрица А = (А1, А2,...Аn) называется невырожденной, если векторы-столбцы являются линейно независимыми. Число линейно независимых векторов-столбцов матрицы называется рангом матрицы . Поэтому можно сказать, что для того, чтобы существовала обратная матрица, необходимо и достаточно, чтобы ранг матрицы равнялся ее размерности, т.е. r = n. Алгоритм нахождения обратной матрицы Записать в таблицу для решения систем уравнений методом Гаусса матрицу А и справа (на место правых частей уравнений) приписать к ней матрицу Е. Используя преобразования Жордана, привести матрицу А к матрице, состоящей из единичных столбцов; при этом необходимо одновременно преобразовать матрицу Е. Если необходимо, то переставить строки (уравнения) последней таблицы так, чтобы под матрицей А исходной таблицы получилась единичная матрица Е. Записать обратную матрицу А-1, которая находится в последней таблице под матрицей Е исходной таблицы. Пример. Для матрицы А найти обратную матрицу А-1 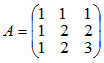 Решение: Записываем матрицу А и справа приписываем единичную матрицу Е. Используя преобразования Жордана, приводим матрицу А к единичной матрице Е. Вычисления приведены в таблице 31.1. 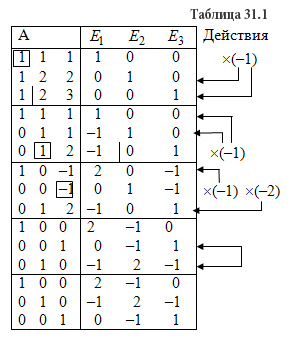 Проверим правильность вычислений умножением исходной матрицы А и обратной матрицы А-1. 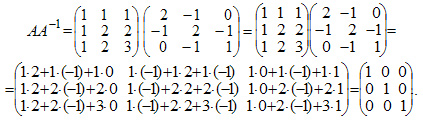 В результате умножения матриц получилась единичная матрица. Следовательно, вычисления произведены правильно. Ответ: 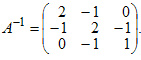 Определитель матрицы
Для любой квадратной матрицы может быть найдена величина, называемая определителем. Определитель — это квадратная таблица чисел или математических символов (Δd). Для матрицы второго порядка 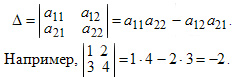 определитель вычисляется по формуле: Разложение по строке или столбцу Формулы разложения по строке или столбцу: 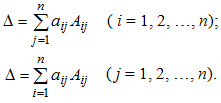 Первые n формул называются формулами разложения определителя по строке, а вторые n формул называются формулами разложения определителя по столбцу. В этих формулах  - алгебраические дополнения элементов аij матрицы А, где Mij — миноры элементов аij матрицы А.Минором Mij элемента аij матрицы n-го порядка А называется определитель матрицы (n-1)-го порядка, получаемой из матрицы А вычеркиванием i-й строки и j-го столбца, на пересечении которых находится элемент aij/ 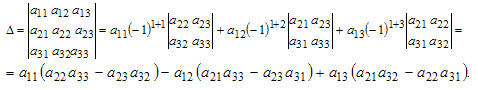 Правило Саррюса Дописывание двух первых строк или столбцов. 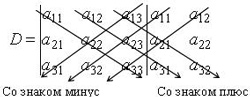 В этом случае считаем так: a11*а22*а33 + а12*а23*31+а13*а21*а32 — а13*а22*а31 — а11*а23*а32 — а12*а21*а33 Пример Вычислить определитель 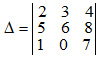 двумя способами: с помощью разложения по первой строке и по правилу треугольника.Решение: 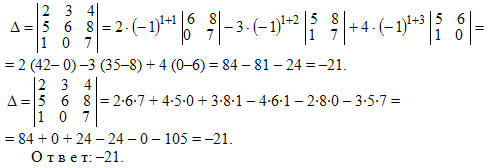 Свойства определителей Свойство 1. Определитель не изменится, если все строки заменить соответствующими столбцами и наоборот.  Свойство 2. При перестановке двух каких-либо строк или столбцов местами определитель изменяет знак.  Свойство 3. Определитель равен нулю, если он имеет две равные строки (столбца). Свойство 4. Множитель, общий для всех элементов строки или столбца, можно выносить за знак определителя.  Свойство 5. Если к элементам какой-либо строки или столбца прибавить соответствующие элементы другой строки или столбца, то определитель не изменится. Следствие из свойств 32.4 и 32.5: Если к элементам какой-либо строки или столбца прибавить соответствующие элементы другой строки или столбца, умноженные на некоторое число, то определитель не изменится. Свойство 6. Сумма произведений элементов какой-либо строки или столбца на алгебраические дополнения соответствующих элементов другой строки или столбца равна нулю. Пример. Вычислить определитель, используя свойства:  Решение: 1. Третью строку умножим на подходящие множители и прибавим к остальным: 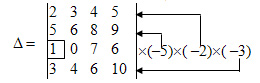 получим: 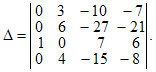 Метод Крамера Решение систем уравнений Пусть имеется система уравнений: 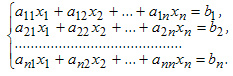 Обозначим через Δ определитель матрицы системы и через Δj определитель, который получается из определителя Δ заметой j-го столбца столбцом правых частей системы ( j=1,2,...n). 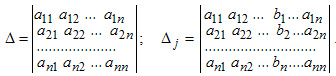 Теорема. Если определитель матрицы отличен от нуля, т.е. Δ ≠0, то система имеет единственное решение, которое находится по формуле:  ТЕМА 6. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ ВЕРОЯТНОСТЬ. ТЕОРЕМЫ СЛОЖЕНИЯ И УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ Основные понятия комбинаторики В разделе математики, который называется комбинаторикой, решаются некоторые задачи, связанные с рассмотрением множеств и составлением различных комбинаций из элементов этих множеств. Например, если взять 10 различных цифр 0, 1, 2, 3,: , 9 и составлять из них комбинации, то будем получать различные числа, например 143, 431, 5671, 1207, 43 и т.п. Мы видим, что некоторые из таких комбинаций отличаются только порядком цифр (например, 143 и 431), другие - входящими в них цифрами (например, 5671 и 1207), третьи различаются и числом цифр (например, 143 и 43). Таким образом, полученные комбинации удовлетворяют различным условиям. В зависимости от правил составления можно выделить три типа комбинаций: перестановки, размещения, сочетания. Предварительно познакомимся с понятием факториала. Произведение всех натуральных чисел от 1 до n включительно называют n-факториаломи пишут . Пример. Вычислить: а) ; б) ; в) . Решение. а)  .б) Так как  и  , то можно вынести за скобки  Тогда получим  .в)  .Перестановки Комбинация из n элементов, которые отличаются друг от друга только порядком элементов, называются перестановками. Перестановки обозначаются символом Рn, где n- число элементов, входящих в каждую перестановку. (Р - первая буква французского слова permutation- перестановка). Число перестановок можно вычислить по формуле  или с помощью факториала:  Запомним, что 0!=1 и 1!=1. Пример. Сколькими способами можно расставлять на одной полке шесть различных книг? Решение. Искомое число способов равно числу перестановок из 6 элементов, т.е.  .Размещения Размещениями из m элементов в n в каждом называются такие соединения, которые отличаются друг от друга либо самими элементами (хотя бы одним), либо порядком из расположения. Размещения обозначаются символом  , где m- число всех имеющихся элементов, n- число элементов в каждой комбинации. (А-первая буква французского слова arrangement, что означает "размещение, приведение в порядок").При этом полагают, что n  m.Число размещений можно вычислить по формуле  ,т.е. число всех возможных размещений из m элементов по n равно произведению n последовательных целых чисел, из которых большее есть m. Запишем эту формулу в факториальной форме:  .Пример. Сколько вариантов распределения трех путевок в санатории различного профиля можно составить для пяти претендентов? Решение. Искомое число вариантов равно числу размещений из 5 элементов по 3 элемента, т.е.  .Сочетания Сочетаниями называются все возможные комбинации из m элементов по n, которые отличаются друг от друга по крайней мере хотя бы одним элементом (здесь m и n-натуральные числа, причем n m).Число сочетаний из m элементов по n обозначаются  (С-первая буква французского словаcombination - сочетание).В общем случае число из m элементов по n равно числу размещений из m элементов по n, деленному на число перестановок из n элементов:  Используя для чисел размещений и перестановок факториальные формулы, получим:  Пример. В бригаде из 25 человек нужно выделить четырех для работы на определенном участке. Сколькими способами это можно сделать? Решение. Так как порядок выбранных четырех человек не имеет значения, то это можно сделать  способами.Находим по первой формуле  .Кроме того, при решении задач используются следующие формулы, выражающие основные свойства сочетаний:   (по определению полагают  и  ); . |