Задачник. Методика расчета статистических показателей здоровья населения и деятельности учреждений здравоохранения
 Скачать 0.88 Mb. Скачать 0.88 Mb.
|
|
1.2. Средние величины. Оценка достоверности результатов исследований Эталонные задачи Задача 1 Для нормирования труда медицинской сестры процедурного кабинета хирургического отделения старшей медицинской сестрой в течение месяца проводился хронометраж затрат рабочего времени на подготовку кабинета к работе. Получены следующие результаты (в минутах): 30, 23, 28, 25, 25, 27, 26, 24, 22, 25, 20, 27, 28, 24, 21, 26, 25, 24,27, 26, 23, 25, 21, 22, 26, 25, 24, 25, 29. Постройте вариационный ряд, назовите его основные характеристики. Рассчитайте средние затраты рабочего времени на подготовку процедурного кабинета. Дайте оценку изменчивости (вариабельности) признака в данном вариационном ряду. Проведите анализ достоверности и точности полученных результатов. Решение эталонной задачи 1: Строим вариационный ряд, размещая значение признака (затраты рабочего времени) в порядке возрастания и подсчитываем частоты встречаемость различных значений:
Основные характеристики построенного вариационного ряда: V - (варианта) – числовое значение признака (в минутах). P - (частота) – частота встречаемости каждого признака в вариационном ряду. A - (амплитуда) – разность между значениями максимальной и минимальной вариант (Vmax – Vmin). A = 10 мин. i - (интервал) – разность между соседними вариантами. i = 1 мин. Mo - (мода) – наиболее часто встречающаяся варианта. Mo = 25 мин. Me - (медиана) – варианта, делящая вариационный ряд пополам. Me = 25 мин. В нашем случае мода совпадает с медианой. Член ряда – варианта со своей частотой (V и P). N – количество наблюдений (30). Для расчета средних затрат рабочего времени необходимо рассчитать среднюю арифметическую взвешенную, поскольку Р ≠ const. Формула для расчета: М = 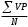 , , М = 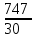 = 24,9 ≈ 25 минут, = 24,9 ≈ 25 минут, Промежуточные расчеты удобно производить в таблице:
Для оценки вариабельности признака используется среднее квадратическое отклонение: 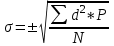 , где , где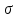 - среднее квадратическое отклонение, - среднее квадратическое отклонение,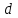 - отклонение варианты от средней, - отклонение варианты от средней,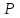 - частота встречаемости признака, - частота встречаемости признака,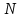 - число наблюдений. - число наблюдений.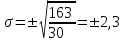 минуты. минуты.Результаты промежуточных расчетов также заносим в таблицу:
Распределение вариант в однородном вариационном ряду подчиняется правилу трех сигм (3 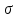 ): если к средней арифметической величине прибавить или отнять 1 ): если к средней арифметической величине прибавить или отнять 1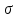 , то при нормальном распределении в этих пределах будет находится не менее 68,3 % всех вариант, что считается нормой для изучаемого явления. В пределах М±2 , то при нормальном распределении в этих пределах будет находится не менее 68,3 % всех вариант, что считается нормой для изучаемого явления. В пределах М±2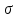 находится 95,5% всех вариант, в пределах М±3 находится 95,5% всех вариант, в пределах М±3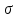 - 99,7% всех вариант. - 99,7% всех вариант.Исследуем вариационный ряд по правилу трех сигм, для этого в обе стороны от средней будем откладывать последовательно по 1 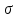 : :
Построенный нами вариационный ряд укладывается в пределы 3 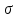 , степень вариабельности признака 99,7%. Результаты исследования достоверны, средняя является типичной для данного вариационного ряда. , степень вариабельности признака 99,7%. Результаты исследования достоверны, средняя является типичной для данного вариационного ряда.Оценка точности статистической величины проводится по величине ее ошибки. 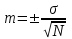 . .Если рассчитанная нами средняя больше или равна утроенному произведению своей ошибки, то ошибка считается малой, несущественной, не влияющей на результат исследований. 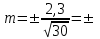 0,4 минуты, 0,4 минуты,М 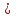 1,2 – неравенство истинное, величиной ошибки можно пренебречь. 1,2 – неравенство истинное, величиной ошибки можно пренебречь.Вывод: Средние затраты рабочего времени на уборку процедурного кабинета составляют 25 минут. Полученный результат достоверен. Величина ошибки не существенна. |

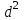 = V-M
= V-M