Задачник. Методика расчета статистических показателей здоровья населения и деятельности учреждений здравоохранения
 Скачать 0.88 Mb. Скачать 0.88 Mb.
|
|
Задача 2 Определите, эффективно ли действие применяемой вакцины «Г», если их 1 400 привитых заболело 140 человек, а в группе 800 человек, не получивших прививку, число заболевших составило 150 человек. Решение эталонной задачи 2: Эффективность действия вакцины можно определить по наличию достоверной разности показателей заболеваемости среди групп привитых и не привитых. Достоверность разности показателей определяется с помощью доверительного коэффициента (t): 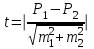 , где , где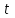 - доверительный коэффициент, коэффициент Стьюдента, - доверительный коэффициент, коэффициент Стьюдента,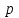 - относительная величина, - относительная величина,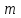 - ошибка относительной величины. - ошибка относительной величины.Рассчитаем долю заболевших среди привитых и не привытых: 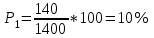 , ,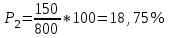 . .Рассчитаем среднюю ошибку относительной величины: 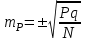 , где , где 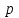 - относительная величина, - относительная величина,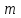 - ошибка относительной величины, - ошибка относительной величины,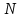 - число наблюдений, - число наблюдений,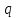 = 100 - = 100 - 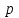 . .Производим расчеты: 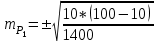 = =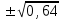 , ,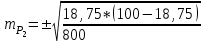 = =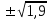 , ,Применяем формулу расчета коэффициента Стьюдента: 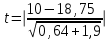 = 5,5. = 5,5.Разность статистически достоверна при величине 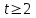 . . Вывод. Рассчитанный коэффициент Стьюдента больше 2, следовательно разность между показателями заболеваемости привитых и не привитых лиц статистически достоверна. Применение вакцины данной эффективно, поскольку позволяет снизить заболеваемость. Ситуационные задачи Задача 1 В поликлинике № 5 за апрель текущего года пролечено 33 человека с диагнозом DS: Острый бронхит. Длительность лечения (в днях): 7, 8, 9, 8, 7, 10, 12, 9, 8, 11, 10, 8, 7, 6, 9, 7, 11, 8, 10, 6, 7, 8, 9, 8, 10, 9, 7, 7, 8, 10, 9, 7, 8. Постройте вариационный ряд, назовите его основные характеристики. Рассчитайте среднюю длительность лечения больных острым бронхитом. Дайте оценку изменчивости признака в данном вариационном ряду. Проведите анализ достоверности полученных результатов. Задача 2 В отчетном году был проведен профилактический осмотр школьников с измерением параметров физического развития. В группе девочек 7 лет получены следующие результаты по массе тела (в кг): 24, 25, 27, 26, 24, 20, 23, 25, 21, 28, 25, 26, 24, 21, 22, 25, 24, 26, 27, 21, 25, 26, 23, 26, 24, 23, 19, 22, 29, 28, 19, 25, 24, 25. Постройте вариационный ряд, рассчитайте средний вес девочек. Оцените достоверность результатов исследования. Задача 3 В больнице были проведены измерения уровня звука, создаваемого изделиями медицинской техники (хирургическая аппаратура, лабораторное, физиотерапевтическое, рентгенологическое оборудование). Получены следующие результаты (в дБ): 56, 55, 48, 54, 60, 49, 55, 56, 61, 54, 55, 60, 51, 55,52,53,57,57,49,52,58,53,60, 52,56,54, 53,55,57, 54,55,54, 50, 50, 51, 51, 52, 53, 55, 56, 58, 59, 56, 57. Постройте вариационный ряд, назовите его основные характеристики. Рассчитайте средний уровень шума. Оцените вариабельность признака в данном вариационном ряду и достоверность результатов исследования. Задача 4 При расчете средней длительности пребывания больных на койке в хирургическом стационаре получен результат 14 дней. Рассчитанное среднее квадратическое отклонение составило 2 дня. Оцените меру разнообразия признака в вариационном ряду и достоверность результатов исследования, если за отчетный период в хирургическом стационаре были пролечены 400 человек. Сравните данные с длительностью госпитализации, указанной в федеральной и территориальной программах государственных гарантий обеспечения граждан бесплатной медицинской помощью. Задача 5 Перед экзаменом у группы студентов общей численностью 64 человека было проведено исследование пульса. Средняя частота пульса составила 84 пульсовых движения в минуту. Рассчитано среднее квадратическое отклонение — 4 пульсовых движения в минуту. Оцените изменчивость признака в вариационном ряду и достоверность результатов проведенного исследования. Задача 6 При 5-дневной рабочей неделе стоматолог-терапевт должен выполнить 25 условных единиц трудоемкости (УЕТ) в смену. Рассчитайте среднедневное число УЕТ, выполненное стоматологом-терапевтом, если в течение месяца зарегистрированы следующие данные (абсолютное число УЕТ в день): 31, 24, 28, 30, 30, 28, 29, 25, 29, 32, 33, 26, 27, 34, 26, 28, 29, 31, 27, 28, 30, 27, 28, 29. Постройте вариационный ряд, охарактеризуйте его. Дайте оценку изменчивости признака в данном вариационном ряду. Определите меру точности полученной средней величины. Задача 7 При проведении профилактического медосмотра у 1 200 студентов педиатрического факультета медицинской академии выявлено 720 заболеваний. Рассчитайте показатель заболеваемости и оцените достоверность результатов исследования. Задача 8 С целью изучения заболеваемости по данным обращаемости с болезнями органов пищеварения у группы из 4 000 детей была проведена выкопировка сведений из «Историй развития ребенка». Зарегистрировано 240 заболеваний данного класса болезней. Рассчитайте показатель заболеваемости по обращаемости с болезнями органов пищеварения и оцените достоверность результатов исследования. Задача 9 Определите, достоверно ли снижение заболеваемости ОРВИ среди детей, если известно, что в январе заболели 1800 человек из 2400, а в феврале - 1550 из 2500 наблюдаемых. Задача 10 Среди учащихся старших классов школы № 199 исследовали частоту пульса (в минуту) во время и после сдачи экзамена. Средняя частота пульса во время сдачи экзамена составила 96,4 пульсовых движения в минуту (m1±3,9), а после экзамена – 76,2 пульсовых движения в минуту (m2±4,1). Определите, достоверно ли снижение частоты пульса после экзамена. Задача 11 В районе Р. за год зарегистрировано 1 800 случаев заболеваний по классу «Болезни нервной системы» у детей первого года жизни. В районе Н. за это же время зарегистрированы 1 600 случаев. Среднегодовая численность детей в возрасте от 0 до 1 года в районе Р. составила 4 500, а в районе Н. – 5 500 человек. Оцените достоверность разности между уровнями заболеваемости. Задача 12 С целью изучения профилактической эффективности новой вакцины против гриппа были сформированы основная и контрольная группы с численностью 600 человек каждая. В контрольной группе, где прививочные мероприятия не проводились, впоследствии 79 человек заболели гриппом. В основной группе гриппом заболели 53 человека. Определите, существенно ли снизилась заболеваемость гриппом вследствие проведенной вакцинации. Целесообразно ли было ее проведение? Задача 13 В стоматологической поликлинике в течение года изучалась противокариесная эффективность зубной пасты «D». В группе лиц (400 человек), регулярно использовавших зубную пасту «D», заболеваемость кариесом составила 68%. Среди 500 человек, составивших контрольную группу и применявших другие зубные пасты, заболеваемость кариесом составила 73%. Определите, является ли существенным влияние употребления зубной пасты «D» на заболеваемость кариесом? Задача 14 Рассчитайте средний объем платных медицинских услуг, проводимых клиникой, если спрос на услуги различного профиля составил (абсолютное число пациентов в день): 11, 17,16, 18, 15, 12, 12, 17, 14,13, 14,16, 18,17, 19,15, 17, 16,19, 15, 16, 17, 18, 18, 13. Постройте вариационный ряд, охарактеризуйте его. Оцените изменчивость признака в данном вариационном ряду. Определите меру точности средней величины. Задача 15 Определите среднее число дней временной нетрудоспособности в цехах №1 и №2 предприятия N. Дайте оценку полученному результату (m и σ).
Существенна ли разность показателей заболеваемости с ВУТ в цехах № 1 и № 2? Задача 16 Определите, эффективно ли действие испытуемого гипотензивного лекарственного препарата, если стойкая нормализация артериального давления зарегистрирована у 260 больных из 400, страдающих гипертонической болезнью и пролеченных с применением данного лекарственного средства, и у 900 из 2 000 человек, получавших традиционное лечение, без применения указанного препарата. Задача 17 Определите, эффективно ли внедрение современных организационных технологий в практическое здравоохранение. Введение сестринского процесса в реабилитацию пациентов (32 человека), перенесших ОНМК, повысило удовлетворенность качеством медицинской помощи до 89,5% респондентов. В группе контроля (30 человек) технологии сестринского процесса не применялись, удовлетворенность качеством медицинской помощи выявлена среди 68,6% опрошенных. 1.3. Прямой метод стандартизации Эталонная задача Примените прямой метод стандартизации и определите, в каком населенном пункте показатели смертности выше с учетом возрастной структуры населения.
Решение эталонной задачи: Прямой метод стандартизации применяется для сравнения показателей, рассчитанных для неоднородных по ряду признаков (пол, возраст, сроки госпитализации, квалификация лечащего врача и т.д.) совокупностей. І. Этап. Расчет общих и специальных интенсивных показателей. В данной задаче – это показатели общей и повозрастной смертности (расчет приведен в разделе «Анализ медико-демографических показателей»). Полученные данные заносим в соответствующие графы таблицы.
ІІ. Этап. Выбор «стандарта» и его «расчет». За стандарт принимают такой показатель, в котором наиболее полно отражаются различия сравниваемых групп. В нашем случае за стандарт примем общую численность населения в пунктах А и В: 10 000 + 10 000 = 20 000, аналогично по каждой возрастной группе. «Расчет стандарта» - определение доли каждой возрастной группе в «стандарте». Исходим из того, что все население составляет 1000 долей, тогда доля возрастной группы 20-29 лет составляет: 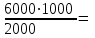 300 долей. 300 долей.Аналогично расчет производим для каждой возрастной группы. Полученные результаты заносим в соответствующие графы таблицы:
ІІІ. Этап. Расчет специальных стандартизированных показателей. В нашем случае специальные показатели – это повозрастные показатели. Из определения смертности следует, что при показателе смертности 5‰ (для возрастной группы в населенных пунктах А и В) из каждой тысячи человек умирает 5. При условии, что «условная» численность группы будет 300 (доля стандарта), составляем пропорцию: 1 000 – 5 300 – Х, Х = 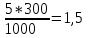 . .Аналогично рассчитываем все повозрастные показатели для каждого населенного пункта. полученные результаты заносим в таблицу:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
