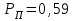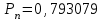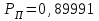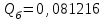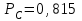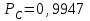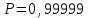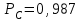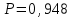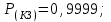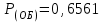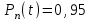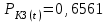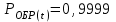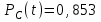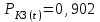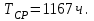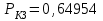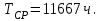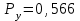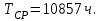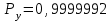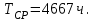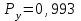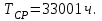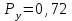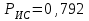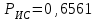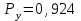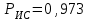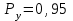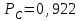Пособие КиНЭС. Министерстерство образования и науки российской федерации
 Скачать 0.95 Mb. Скачать 0.95 Mb.
|
|
Приложение 2 Варианты заданий к расчетной работе № 2. Прибор состоит из пяти блоков, причем выход из строя любого из этих блоков приводит к отказу прибора. Блоки выходят из строя независимо друг от друга. Определить, какую модель следует использовать для определения надежности прибора и чему равна вероятность его исправной работы, если вероятность безотказной работы каждого блока р составляет 0,9. Прибор состоит из пяти блоков. Отказ прибора происходит при выходе из строя первого блока и одновременном выходе из строя всех остальных блоков. Определить, какую модель необходимо использовать для определения надежности прибора и чему равна вероятность его исправной работы, если вероятность безотказной работы каждого блока р составляет 0,9. Построить модель надежности и определить вероятность безотказной работы системы из последовательно соединенных резисторов, приведенной на рис. 1. Тип отказа резисторов — тепловая деструкция, причем все резисторы равнонадежные с вероятностью безотказной работы 0,95. Рис. 1. Схема соединения резисторов к задаче 3. Построить модели надежности и определить вероятности безотказной работы электрических соединений резисторов, показанных на рис. 2, считая все резисторы равнонадежными с вероятностью безотказной работы 0,95. Тип отказа резисторов — тепловая деструкция. 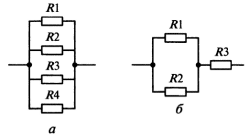 Рис. 2. Схемы (а, б) соединений резисторов к задаче 4. Построить модель надежности и определить вероятность безотказной работы электрического соединения конденсаторов, показанного на рис. 3. Типы отказов конденсаторов — короткое замыкание и обрыв. Все конденсаторы равнонадежны с вероятностью безотказной работы 0,9. Рис. 3. Схема соединений конденсаторов к задаче 5. Используя условия задачи 5 построить модель надежности и определить вероятность безотказной работы схемы соединения конденсаторов, приведенной на рис. 4. 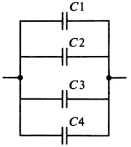 Рис. 4. Схема соединения конденсаторов к задаче 6. Построить модель надежности и определить вероятность безотказной работы схемы соединения резисторов и конденсаторов, изображенной на рис. 5. Все элементы равнонадежны с вероятностью безотказной работы 0,9. Тип отказа конденсаторов — короткое замыкание, а резисторов — тепловая деструкция. Рис. 5. Схема соединения резисторов и конденсаторов к задаче 7. Построить модель надежности и определить вероятность безотказной работы схемы соединения резисторов и конденсаторов, приведенной на рис. 6. Все элементы равнонадежны с вероятностью безотказной работы 0,9. Тип отказа конденсаторов — короткое замыкание, а резисторов — тепловая деструкция. 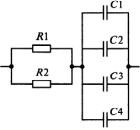 Рис. 6. Схема соединений резисторов и конденсаторов к задаче 8. По структурной модели надежности, показанной на рис. 7, определить вероятность безотказной работы устройства, если вероятности безотказной работы элементов схемы следующие: р1 = 0,95; р2 = 0,9; р3 = 0,92; р4 = 0,9; р5 = 0,8. Рис. 7. Структурная модель надежности устройства к задаче 9. По структурной модели надежности, показанной на рис. 8, определить вероятность безотказной работы устройства, если вероятности безотказной работы элементов схемы следующие: р1 = 0,95; р2 = 0,9; р3= 0,92; р4 = 0,9; р5 = 0,8. 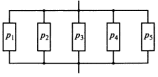 Рис. 8. Структурная модель надежности устройства к задаче 10. По структурной модели надежности, показанной на рис. 9, определить вероятность безотказной работы устройства, если вероятности безотказной работы элементов схемы следующие: р1 = 0,95; р2 = 0,9; р3 = 0,92; р4 = 0,9; р5 = 0,8. 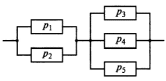 Рис. 9. Последовательно-параллельная модель надежности устройства к задаче 11. По структурной модели надежности, показанной на рис. 10, определить вероятность безотказной работы устройства, если вероятности безотказной работы элементов схемы следующие: р1 = 0,95; р2 = 0,9; р3 = 0,92; р4 = 0,9; р5 = 0,8. 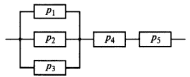 Рис. 10. Последовательно-параллельная модель надежности устройства к задаче 12. По структурной модели надежности, показанной на рис. 11, определить вероятность безотказной работы устройства, если вероятности безотказной работы элементов схемы следующие: р1 = 0,95; р2 = 0,9; р3 = 0,92; р4 = 0,9; р5 = 0,8. 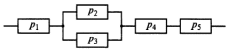 Рис. 11. Последовательно-параллельная модель надежности устройства к задаче 13. По структурной модели надежности, показанной на рис. 12, определить вероятность безотказной работы устройства, если вероятности безотказной работы элементов схемы следующие: р1 = 0,95; р2 = 0,9; р3 = 0,92; р4 = 0,9; р5 = 0,8. 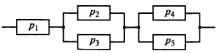 Рис. 12. Последовательно-параллельная модель надежности устройства к задаче 14. По структурной модели надежности, показанной на рис. 13, определить вероятность безотказной работы устройства, если вероятности безотказной работы элементов схемы следующие: p1 = 0,95; р2 = 0,9; р3 = 0,92; р4 = 0,9; р5 = 0,8. 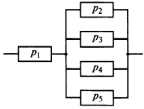 Рис. 13. Последовательно-параллельная модель надежности устройства к задаче 15. По структурной модели надежности, представленной на рис. 14, определить вероятность безотказной работы системы, если p1 = 0,9; р2 = 0,85; р3 = 0,95; р 4 = 0,9. 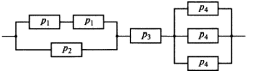 Рис. 14. Структурная модель надежности системы к задаче 16. Прибор состоит из двух блоков, соединенных последовательно (рис. 15). Вероятности отказов этих блоков соответственно q1 = 0,11 и q2 = 0,33. Найти вероятность исправной работы прибора. 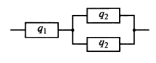 Рис. 15. Параллельно-последовательная модель надежности прибора к задаче 17. Структурная модель надежности блока представлена на рис. 16. Найти вероятность отказа блока, имеющего равнонадежные элементы с вероятностью безотказной работы 0,8. 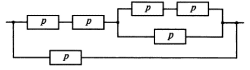 Рис. 16. Параллельно-последовательная модель надежности блока к задаче 18. Найти вероятность безотказной работы системы, структурная модель надежности которой приведена на рис. 17, если 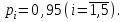 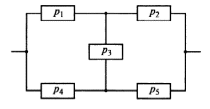 Рис. 17. Сложная модель надежности системы к задаче 19. Решение. Приняв за базовый третий элемент с p3, заменим заданную схему двумя эквивалентными схемами I и II (рис. 18) и определим вероятность безотказной работы каждой из них. , 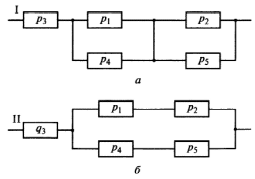 Рис. 18. Параллельно-последовательные эквивалентные модели надежности схемы , приведенной на рис. 17. Вероятность безотказной работы схемы I с равнонадежными элементами равна 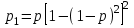 . .Вероятность безотказной работы схемы II равна 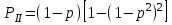 . .Тогда согласно формуле 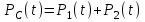 получим получим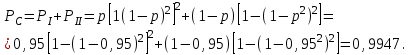 Найти вероятность безотказной работы системы, структурная модель надежности которой приведена на рис. 19, если вероятность безотказной работы каждого из ее узлов p = 0,9. 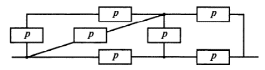 Рис. 19. Сложная модель надежности системы к задаче 20. Найти вероятность безотказной работы системы, структурная модель надежности которой приведена на рис. 20, если вероятности безотказной работы ее узлов составляют p1 = 0,9 и р2 = 0,8. 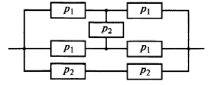 Рис. 20. Сложная модель надежности системы к задаче 21. Найти вероятность безотказной работы прибора, структурная модель надежности которого приведена на рис. 21, если известны вероятности безотказной работы ее узлов: р1 = 0,8; р2 = = 0,85. 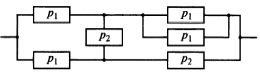 Рис. 21. Сложная модель надежности прибора к задаче 22. Найти вероятность безотказной работы системы, структурная модель надежности которой приведена на рис. 22, если р1 = 0,7 и р2= 0,8. 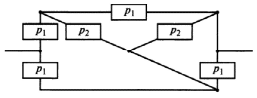 Рис. 22. Сложная модель надежности системы к задаче 23. Структурные модели надежности пяти блоков (I...V) приведены на рис. 23. Вероятности безотказной работы элементов этих блоков подчиняются экспоненциальному закону. Найти среднюю наработку до первого отказа каждой модели, если р1 = 0,95, р2 = 0,9 в течение 1000 ч., и интенсивности их отказов, если р1= р2=0,9 в течение 100 ч. 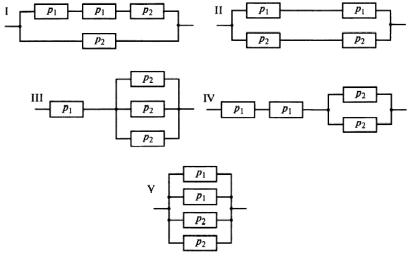 Рис. 23. Структурные модели надежности пяти блоков (I...V) к задаче 24. В структурной модели надежности системы, представленной на рис. 24, р=0,9 , р1=0,8. Определить вероятность безотказной работы этой системы. 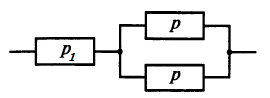 Рис. 24. Структурная модель надежности системы к задаче 25. В структурной модели надежности системы, показанной на рис. 25, р=0,9. Найти вероятность безотказной работы этой системы. Рис. 25. Структурная модель надежности системы к задаче 26. В структурной модели надежности системы, показанной на рис. 26, р=0,7. Найти вероятность безотказной работы этой системы. 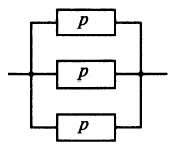 Рис. 26. Структурная модель надежности системы к задаче 27. В структурной модели надежности системы, приведенной на рис. 27, р = 0,9, р1 = 0,95. Найти вероятность безотказной работы системы. 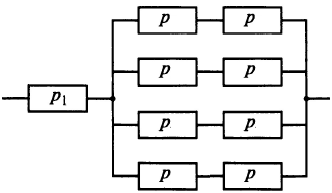 Рис. 27. Структурная модель надежности системы к задаче 28. Ответы к вариантам заданий по расчетной работе №2.
ОГЛАВЛЕНИЕ ПРЕДИСЛОВИЕ ВВЕДЕНИЕ 1.СИСТЕМОТЕХНИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ТЕХНОЛОГИЧЕСКОГО ПРОЦЕССА ПРОИЗВОДСТВА ЭЛЕКТРОННЫХ СРЕДСТВ 2. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ 2.1. Случайные величины. Выборка 2.2. Законы распределения случайных величин 2.3. Основные виды законов распределения для непрерывных случайных величин 2.4. Числовые характеристики случайных величин 2.5. Статистическая проверка гипотез 2.6. Ошибки измерения физических величин и методы их исключения 3. ВЫБОР НАИБОЛЕЕ СУЩЕСТВЕННЫХ ФАКТОРОВ ОБЪЕКТА МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ 3.1. Метод экспертных оценок 3.2. Метод начальных моментов 3.3. Дисперсионный анализ 4. КАЧЕСТВО ЭЛЕКТРОННЫХ СРЕДСТВ 4.1. Основные сведения об электронном средстве и показателях его качества 4.2. Система управления качеством электронных средств 4.3. Себестоимость и уровень качества электронных средств 4.4. Контроль качества электронного средства 4.5. Структурная схема системы управления качеством электронных средств 4.6. Статистические методы анализа качества электронных средств 4.6.1. Контрольный лист 4.6.2. Графические методы 4.6.3. Диаграмма разброса ( поле корреляции ) 4.6.4. Метод расслаивания 4.6.5. Диаграмма Парето 4.6.6. Причинно – следственная диаграмма 4.6.7. Статистический контроль качества электронных средств на основе контрольных карт 4.6.7.1. Виды статистического контроля 4.6.7.2. Контрольная карта для средних значений 4.6.7.3. S – карта и R – карта 4.6.7.4. Контрольная карта для количественных признаков 4.6.7.5. Контрольная карта для качественных признаков 4.7. Автоматизированные системы контроля качества электронных средств 4.8. Прогнозирование качества электронных средств 5. НАДЕЖНОСТЬ ЭЛЕКТРОННЫХ СРЕДСТВ 5.1. Основные понятия в теории надежности электронных средств 5.2. Количественные показатели надежности электронных средств 5.2.1. Единичные показатели надежности 5.2.2. Комплексные показатели надежности 5.3. Методика расчета надежности электронного средства по внезапным отказам 5.4. Резервирование электронных средств ЗАКЛЮЧЕНИЕ БИБЛИОГРАФИЧЕСКИЙ СПИСОК ПРИЛОЖЕНИЯ Учебное издание ЗАХАРОВ Юрий Владимирович КАЧЕСТВО И НАДЕЖНОСТЬ ЭЛЕКТРОННЫХ СРЕДСТВ УЧЕБНОЕ ПОСОБИЕ Редактор Л.С.Журавлева Компьютерная верстка С.Н.Эштыкова Дизайн обложки С.Н.Эштыкова | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||