Пособие КиНЭС. Министерстерство образования и науки российской федерации
 Скачать 0.95 Mb. Скачать 0.95 Mb.
|
|
2.3. ОСНОВНЫЕ ВИДЫ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ДЛЯ НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН РАВНОВЕРОЯТНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ Простейшим распределением для непрерывной СВ Х является равновероятный закон распределения с плотностью распределения f(x) вида: 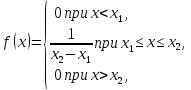 где х1 и х2 – пределы изменения СВ Х. Тогда: 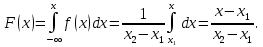 Равновероятный закон распределения СВ применяется в теории надежности ЭС. ЭКСПОНЕНЦИАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ Распределение СВ Х подчиняется экспоненциальному закону, если плотность распределения f(x) имеет вид: 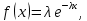 где λ – интенсивность случайного события – постоянная величина. Тогда функция распределения: 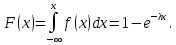 Характерный признак этого распределения - постоянство значения λ. Экспоненциальный закон используется при математическом моделировании зависимости показателя качества ЭС от определяющих его численную величину факторов, когда более поздним измерениям (по времени) показателя качества придается больший «вес» по сравнению с ранними. Он широко применяется при расчете надежности нерезервированных изделий по внезапным отказам, вызванных большим количеством входящих в их состав комплектующих элементов. НОРМАЛЬНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ Нормальный закон распределения (НЗР) – наиболее часто встречающийся на практике вид распределения СВ при решении задач оценки и управления качеством ЭС. В теории надежности с помощью НРЗ описывается работоспособность ЭС в процессе износа и физического « старения» материалов и электрорадиоэлементов, а также при возникновении отказов из-за ухода показателей качества изделия за пределы заданных допусков вследствие воздействия климатических и механических факторов. Анализ общих условий возникновения НЗР показывает, что если отклонение показателя качества изделия γ от номинального значения вызвано действием достаточно большого числа k независимых или слабо зависимых факторов xi 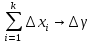 и среди k факторов нет явно превалирующих над остальными, то закон распределения параметра γ при увеличении k стремится к нормальному. Причем закон распределения факторов xi может быть любым. Это утверждение является следствием центральной предельной теоремы теории вероятностей (теоремы Ляпунова). Для нормального закона распределения случайной величины Х : 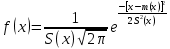 ; ;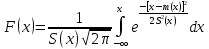 . .В этих выражениях m(x) и s(x) – выборочные математическое ожидание и среднее квадратическое отклонение СВ Х. Из выражения для функции распределения F(x) можно найти вероятность нахождения непрерывной СВ в пределах значений x1 и x2: 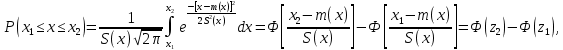 где Ф(z)– нормированная функция Лапласа. Значения функции Ф(z) табулированы [2]. Из приведенного выражения можно вычислить вероятность нахождения СВ Х в пределах: ±S; ±2S; ±3S. Они равны соответственно: 0,683; 0,955; 0,9973. Практически рассеяние СВ, подчиненной НЗР, находится в пределах m(x)±3S(x), т.к. вероятность попадания за пределы этого участка очень мала (0,0027), т.е. такое событие можно считать практически невозможным. Отсюда следует правило «трех сигм»: если случайная величина Х имеет нормальный закон распределения, то отклонение ее значений от математического ожидания по абсолютной величине не превосходит утроенного среднеквадратического отклонения S (S – выборочная оценка σ (сигмы)).  2.4.ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН ХАРАКТЕРИСТИКИ ПОЛОЖЕНИЯ 1. Математическое ожидание – среднее значение СВ в генеральной совокупности. Оно характеризует центр распределения СВ Х. Статистическое (выборочное) значение математического ожидания вычисляется по формуле: 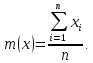 2. Медиана Me – значение СВ, которое делит упорядоченный ряд статистических данных на две равные по объему группы. Если в упорядоченном ряде нечетное (2k+1) число значений статистических данных, то значение xk+1 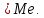 Если в упорядоченном ряде четное (2k) число значений статистических данных, то значение 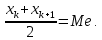 3. Мода Mo – значение СВ, которое наиболее часто встречается в наблюдаемом ряде статистических данных. Бывают одномодальные, двумодальные и многомодальные распределения. ХАРАКТЕРИСТИКИ РАССЕЯНИЯ 1.Размах ( R ) статистических данных: 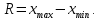 2.Центр интервала статистических данных (xср.): 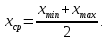 3.Дисперсия – математическое ожидание квадрата отклонения СВ от среднего значения. Она характеризует степень рассеяния СВ Х от среднего значения m(x). Статистическое (выборочное) значение дисперсии вычисляется по формуле: 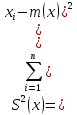 4.Среднеквадратическое отклонение (S). S – корень квадратный от дисперсии; имеет ту же размерность, что и СВ Х: 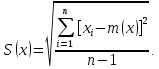 5.Коэффициент вариации (V). Характеризует рассеивание СВ Х в относительных единицах ( безразмерная величина или значение, выраженное в процентах). 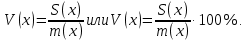 2.5. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ Под статистическими понимают гипотезы, которые относятся к отдельным параметрам закона распределения СВ Х или к самому закону. В теории простых гипотез проверяемую гипотезу обозначают через Н0 и называют ее нулевой гипотезой. Конкурирующую гипотезу называют альтернативной и обозначают Н1. ГИПОТЕЗА О РАВЕНСТВЕ ДИСПЕРСИЙ Берутся две выборки изделий объемом n1 и n2. У изделий контролируется показатель качества Х и вычисляются значения 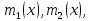 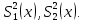 Нулевая гипотеза Н0: 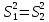 . .Альтернативная - Н1: 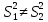 . .При НЗР параметра Х для проверки гипотезы Н0 используется F-критерий Фишера. Для этого: а) вычисляется Fрасч.. 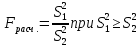 , ,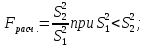 (1) (1)б) определяется табличное значение Fтабл. 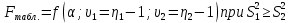 , ,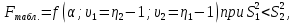 где α – уровень принимаемого решения , 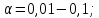 в) сравниваются Fрасч.. и Fтабл.. Если Fрасч..<Fтабл., то гипотеза о равенстве дисперсий в двух выборках справедлива с вероятностью 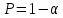 . .Если Fрасч..≥Fтабл., то с вероятностью 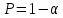 верна гипотеза Н1. верна гипотеза Н1.ГИПОТЕЗА ОБ ОДНОРОДНОСТИ ДИСПЕРСИЙ Для k выборок одинакового объема n по результатам контроля показателя качества Х вычислены дисперсии 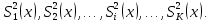 Необходимо проверить отличается ли хотя бы одна выборка по дисперсии от остальных. Необходимо проверить отличается ли хотя бы одна выборка по дисперсии от остальных.Гипотеза Н0: дисперсии однородны (нет отличия ). Гипотеза Н1: дисперсии неоднородны (отличаются друг от друга). Для проверки гипотезы используется G-критерий: а) находится 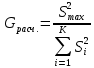 , ,где 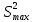 - максимальная дисперсия из вычисленных; - максимальная дисперсия из вычисленных;б) определяется табличное значение Gтабл. 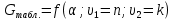 ; ;в) сравниваются Gрасч. иGтабл. Если Gрасч.<Gтабл., то принимается гипотеза Н0 с вероятностью Р=1-α. Если Gрасч.≥Gтабл., то принимается гипотеза Н1 с вероятностью Р=1-α. ГИПОТЕЗА О РАВЕНСТВЕ СРЕДНИХ Берутся две выборки изделий объемом n1 и n2. По результатам контроля показателя качества Х вычисляются значения 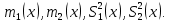 Нулевая гипотеза Н0 :(выборки не отличаются по средним значениям),т.е. 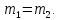 Альтернативная гипотеза Н1: 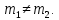 Для проверки гипотезы используется t-критерий Стьюдента. Для этого: а) проверяется равенство дисперсий (см. гипотезу о равенстве дисперсий); б) вычисляется расчетное значение tрасч. 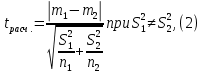 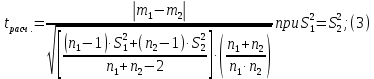 в) определяется tтабл.=f(α,υ), где 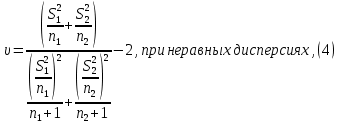 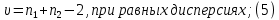 г) сравниваются tрасч.иtтабл.. Если tрасч.<tтабл., то принимается гипотеза Н0 с вероятностью Р=1-α. Если tрасч.≥tтабл., то принимается гипотеза Н1 с вероятностью Р=1-α. ГИПОТЕЗА О ЗАКОНЕ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ 1. Для проверки соответствия экспериментальных данных нормальному закону распределения используется критерий Колмогорова. Для этого: а) строится эмпирическая функция распределения F*(x) по выборке объемом n в интервале xmin≤X≤xmax (см. раздел 2.2); б) строится теоретическая функция распределения F(x) в интервале xmin≤X≤xmax, путем нахождения величин 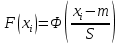 для всех q интервалов, где xi – среднее значение i-го интервала (i=1,2,…,q) , а Ф(z) – табулированная функция Лапласа [2]; для всех q интервалов, где xi – среднее значение i-го интервала (i=1,2,…,q) , а Ф(z) – табулированная функция Лапласа [2];в) функции F*(x) и F(x) наносятся на один график; г) определяется максимальная величина модуля разности между F*(x) и F(x): 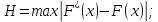 д) определяется вспомогательная величина 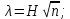 е) определяется вероятность 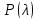 из таблицы: из таблицы:
ж) если 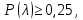 то принимается гипотеза: экспериментальное распределение статистических данных СВ Х подчиняется нормальному закону. то принимается гипотеза: экспериментальное распределение статистических данных СВ Х подчиняется нормальному закону.2. Оценку соответствия экспериментальных данных нормальному закону распределения можно осуществить, используя критерий Пирсона. Сущность критерия: а) строится распределение СВ Х в интервале xmin≤X≤xmax(см. раздел 2.2); б) вычисляется 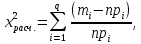 где q – число интервалов длиной l; mi – число значений СВ Х, попавших в i-й интервал; n – объем выборки; 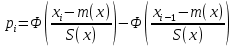 – вероятность попадания СВ Х в i-й интервал , Φ (z) – табулированная функция Лапласа [2] ; – вероятность попадания СВ Х в i-й интервал , Φ (z) – табулированная функция Лапласа [2] ;в) определяется табличное значение 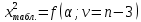 , где , где 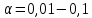 . Значения . Значения 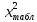 табулированы [2]; табулированы [2];г) сравниваются 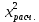 и и 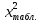 . .Если 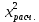 < < 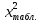 , то с вероятностью Р=1-α принимается гипотеза: экспериментальное распределение СВ Х подчиняется нормальному закону; если , то с вероятностью Р=1-α принимается гипотеза: экспериментальное распределение СВ Х подчиняется нормальному закону; если 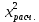 ≥ ≥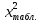 , то с вероятностью Р=1-α оно не соответствует нормальному закону распределения. , то с вероятностью Р=1-α оно не соответствует нормальному закону распределения.2.6. ОШИБКИ ИЗМЕРЕНИЯ ФИЗИЧЕСКИХ ВЕЛИЧИН И МЕТОДЫ ИХ ИСКЛЮЧЕНИЯ При обработке экспериментальных данных, полученных по результатам измерения показателей качества ЭС , возникает задача их анализа и исключения аномальных результатов (ошибок), если есть сомнения в их наличии. В зависимости от причин, их вызывающих, ошибки делят на случайные, систематические и грубые (промахи). СЛУЧАЙНЫЕ, СИСТЕМАТИЧЕСКИЕ И ГРУБЫЕ ОШИБКИ Под случайными понимают ошибки, численные значения которых непредсказуемо меняются от одного опыта к другому. Они являются следствием ошибок при применении контрольно-измерительных приборов для измерений, случайных ошибок экспериментатора, неточных соблюдений методики измерения, непостоянством самой контролируемой величины. Для количественной оценки случайных ошибок применяют математический аппарат теории вероятностей и математической статистики. Наиболее полно случайные ошибки могут быть оценены функцией их распределения с последующей статистической обработкой экспериментальных данных. Отличие систематической ошибки от случайной состоит в том, что ее значение остается постоянным при проведении серии однотипных измерений. Причины возникновения случайных ошибок обычно бывают известны, следовательно, они могут быть исключены из окончательного результата, если их величина предварительно определена. К систематическим ошибкам можно отнести: ошибки эталонов, по которым проградуированы контрольно-измерительные приборы; ошибки, связанные с методикой измерения вследствие неучета температурных и других поправок; применения приближенных формул расчета ; «личные» ошибки экспериментатора, т.е. присущие данному лицу и др. Различают постоянные (неизменные во времени) и прогрессирующие (возрастающие или убывающие во времени) систематические ошибки. Грубые ошибки (аномальные результаты) являются результатом нарушения условий и процесса измерений. Их характерным признаком является резкое отличие одного (нескольких) экспериментальных данных от остальных результатов. Повторение эксперимента (если это возможно) является наиболее надежным, достоверным и эффективным способом обнаружения грубых ошибок. Современные математические методы обработки результатов экспериментальных данных базируются на вероятностном подходе и считается, что ошибки измерения показателей качества ЭС являются случайными. При этом необходимым условием является то, что к началу этой обработки все грубые и систематические ошибки выявлены и устранены. Рассмотрим практический метод исключения грубых ошибок, если их не удалось исключить в процессе проведения измерений показателей качества ЭС. МЕТОД ИСКЛЮЧЕНИЯ РЕЗКО ВЫДЕЛЯЮЩИХСЯ РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА |
