Пособие КиНЭС. Министерстерство образования и науки российской федерации
 Скачать 0.95 Mb.
|
0,33), представляющих два технических направления: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Эксперт | Параметры | ||||||||||||||||
| А | Б | В | Г | Д | Е | Ж | З | ||||||||||
| Группа I | 1 | 3 | 4 | 6 | 1 | 7 | 8 | 5 | 2 | ||||||||
| 2 | 4 | 3 | 7 | 1 | 5,5 | 8 | 5,5 | 2 | |||||||||
| 3 | 4 | 3 | 5 | 1,5 | 7 | 8 | 6 | 1,5 | |||||||||
| 4 | 4 | 3 | 5,5 | 1,5 | 8 | 7 | 5,5 | 1,5 | |||||||||
| 5 | 3,5 | 3,5 | 5,5 | 1,5 | 7 | 8 | 5,5 | 1,5 | |||||||||
| Группа II | 6 | 1 | 3 | 4 | 2 | 6,5 | 8 | 6,5 | 5 | ||||||||
| 7 | 2,5 | 4 | 7 | 2,5 | 6 | 8 | 5 | 1 | |||||||||
| 8 | 3 | 4 | 5 | 1 | 7,5 | 7,5 | 6 | 2 | |||||||||
| 9 | 2,5 | 2,5 | 5 | 1 | 7 | 7 | 7 | 4 | |||||||||
В строках табл.4 записаны нормализованные ранги j-го эксперта (j=1, 2, …,F; F=9) по i-му параметру (i=1, 2, …,M; M=8). Нормализация рангов осуществляется при наличии «связанных» рангов.
Например, девятый эксперт произвел следующую ранжировку параметров:
Параметр А Б В Г Д Е Ж З
Ранжировка 2 2 4 1 5 5 5 3 .
Параметры А и Б при ранжировании по натуральному ряду М=1(1)8 поделили между собой 2 и 3 места. Значит им приписывается ранг
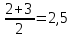. Параметры Д, Е, Ж поделили между собой 6, 7, 8 места; им приписывается ранг 
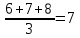. Таким образом получим правильную ранжировку для девятого эксперта в виде:Параметр А Б В Г Д Е Ж З
Ранжировка 2,5 2,5 5 1 7 7 7 4 .
Аналогичным способом получены ранжировки параметров всеми остальными экспертами (если у них были «связанные ранги») в табл.4.
После обработки данных табл.4 получены следующие результаты (расчеты производились по формулам пункта 4 алгоритма метода); они представлены в табл.5.
Таблица 5
Сумма рангов и коэффициент весомости параметров
| Параметр h, β | А | Б | В | Г | Д | Е | Ж | З |
| hi | 27,5 | 30 | 50 | 13 | 61,5 | 69,5 | 52 | 20,5 |
| βi | 0,74 | 0,71 | 0,43 | 0,94 | 0,27 | 0,16 | 0,4 | 0,84 |
Вычислены:
W=0,88;
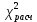=55,5.Табличное значение статистики χ2 для степеней свободы v=7 и уровня значимости α=0,01 равно 18,475. Так как
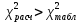, то с вероятностью 0,99 можно утверждать, что результаты расчетов не противоречат предположению о согласованности специалистов относительно информативности параметров, степень которой определена коэффициентом конкордации W=0,88.Учитывая, что ранжирование параметров проведено экспертами, представляющими две группы специалистов, можно оценить степень согласованности их между собой, используя коэффициент ранговой корреляции Спирмэна ρ [3]
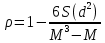,где S(d2) – сумма квадратов разности сопоставляемых пар в ранжировках;
М – число сопоставляемых пар в ранжировках, равное числу параметров.
Величина ρ может принимать значения в диапазоне от -1 до +1; при отсутствии связи между группами эта величина равна 0.
В случае наличия « связанных» рангов:
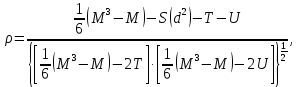
где
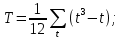
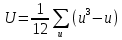;t, u – число одинаковых рангов в первой (Z) и второй (Y) ранжировках.
При M>10 для оценки значимости коэффициента ранговой корреляции используется нормальный закон распределения частот появления каждого значения величины ρ и применяется соотношение [3]:
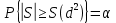,где α - вероятность, что
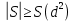.Коэффициент ρ считается значимым, если расчетное значение суммы квадратов разностей
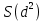меньше табличного 
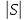, полученного при заданных уровнях значимости α и М.Если M≤10, то распределение частот отличается от нормального закона распределения, и этим пренебречь нельзя. В этом случае используются специальные таблицы распределения частот [3].
Проведя отдельно ранжирование параметров по их информативности для групп I и II (по данным табл.4) и учтя результаты, полученные для всех экспертов совместно (табл.5), приходим к результатам, представленным в табл.6.
Таблица 6
Сводные результаты экспертизы
| Вид ранжировки | Параметры | W при α=0,01 | ||||||||
| А | Б | В | Г | Д | Е | Ж | З | |||
| X (F=9) | 3 | 4 | 5 | 1 | 7 | 8 | 6 | 2 | 0,88 | |
| Z (FI=5) | 4 | 3 | 6 | 1 | 7 | 8 | 5 | 2 | 0,92 | |
| Y (FII=4) | 2 | 4 | 5 | 1 | 7 | 8 | 6 | 3 | 0,95 | |
Коэффициент ранговой корреляции для ранжированных рядов Z и Y (табл.6) равен ρZY=0,905. Задаваясь уровнем значимости α=0,01, при М=8 из [3] находим, что
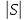=18. Так как 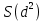=8 <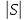 , коэффициент ρZY=0,905 можно считать значимым и гипотезу о наличии связи между ранжировками справедливой.Аналогично можно вычислить коэффициенты для ранжированных рядов (ZX) и (YX). Получим ρZX=0,952, ρYX=0,976, значимые при α=0,01.
На основе рассчитанных коэффициентов весомости βi (табл.5) и при установлении статистической значимости коэффициента конкордации проводится анализ результатов для выбора наиболее информативных параметров. Для этого вычисляется средний коэффициент весомости
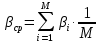и выбираются все параметры, значения βi которых превосходят по величине βср.В данном случае βср=0,562 и наиболее информативными параметрами, характеризующими качество вычитающих потенциалоскопов, будут: Г, З, А, Б.
3.2.МЕТОД НАЧАЛЬНЫХ МОМЕНТОВ
Известно [4], что нестабильные параметры содержат больше информации об объекте, чем стабильные.
Мерой нестабильности показателя качества электронного средства, является значимое расхождение его среднего значения m или дисперсии s2 (или обоих этих показателей совместно) от базовых величин
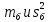. Поэтому, если получить количественную характеристику 
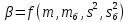, показывающую степень значимости расхождения средних значений m и mб с учетом s2 и 
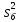, то ее можно использовать для выбора информативных показателей качества ЭС. В качестве основы получения величины β предлагается t – критерий Стьюдента. Математический аппарат данного критерия рассмотрен в разделе 2.5 пособия при проверке гипотезы о равенстве средних m1 и m2.
Алгоритм метода
1. По результатам контроля показателя качества y все изделия делятся на два класса (соответствующие и несоответствующие требованиям нормативно-технической документации или по уровню качества: отличные и хорошие; отличные и удовлетворительные и т. д.).
2. Вычисляются выборочные средние значения и дисперсии каждого исследуемого показателя для 1 и 2 классов:
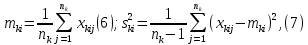
где xkij – измеренное значение i-го показателя у j-го изделия, принадлежащего k-му классу; i=1, 2, …, M, M – число факторов; j = 1, 2, …, nk , nk – число изделий в k-м классе; k=1, 2 – номер класса.
3. Проверяется гипотеза о равенстве дисперсий для каждого i-го показателя на основе F-критерия Фишера (см. раздел 2.5 пособия).
4. Вычисляются расчетные значения tрасч. исследуемых показателей по формуле (2) или (3). Выбор формулы для вычисления tрасч. зависит от результатов, полученных в п.3.
5. Определяются табличные значения
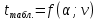.6. Отбираются показатели, для которых выполняется неравенство tрасч.>tтабл..
7. Для отобранных показателей качества ЭС находится коэффициент весомости
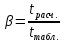и осуществляется их упорядоченность по степени убывания значения β, т. е. в порядке убывания их информативности.