Пособие КиНЭС. Министерстерство образования и науки российской федерации
 Скачать 0.95 Mb. Скачать 0.95 Mb.
|
|
Критерий Романовского. Имеется упорядоченный статистический ряд измеренных значений случайной величины Х: x1, x2, …, xi, …, xn. x1=xmin; xn=xmax. Здесь: x1 или (и) xn – значения, которые вызывают сомнения (резко отличаются от остальных измерений). В практических случаях в качестве x1 и xn может быть несколько измерений, т.е. их может быть ≥2; n – объем выборки. Сущность критерия: а) вычисляется 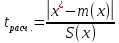 , , где x* - резко выделяющееся значение, в качестве которого взято значение (несколько значений) x1 или (и) xn; m(x) и s(x) – выборочные математическое ожидание и среднее квадратическое отклонение, вычисленные без значения (нескольких значений) х* при объеме выборки n-1 (или n-≥2, если несколько измерений имеют значение х*); б) определяется 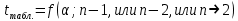 из табл.1 из табл.1Таблица 1 Табличные значения критерия Романовского
в) сравниваются tрасч. и tтабл. . Если tрасч.> tтабл., то с вероятностью Р=1-α значение x* статистического ряда не принадлежит к рассматриваемой совокупности СВ Х и оно должно быть исключено при обработке экспериментальных данных. В дальнейшем эта процедура повторяется со значением, находящимся рядом с x*, пока не будут исключены все аномальные экспериментальные данные. Пример. При анализе изготовления электронного средства для n независимых равноточных измерений показателя качества ( без резко выделяющегося значения xn=xmax ) получено среднее значение m(x)=8,6 и среднее квадратическое отклонение s(x)=0,121. Известно , что n измерение дало результат xn=x*=8,92. Необходимо выяснить с вероятностью P=0,98, является ли этот результат аномальным результатом , если n=61. Решение. Вычислим 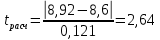 . . Из табл.1 имеем: 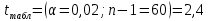 . .Поскольку 2,64>2,4, то это означает, что измерение х61=8,92 является аномальным ( с вероятностью 0,98) и должно быть исключено при обработке экспериментальных данных. Следующий этап исследования – проверка на аномальность значения x60. Вопрос решился бы иначе, если бы, например, число измерений в результате эксперимента равнялось 11. В этом случае по табл.1 имеем: 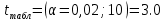 . Поскольку 2,64<3,0, то исключать х*=х11=8,92 не следует из полученного ряда измерений. . Поскольку 2,64<3,0, то исключать х*=х11=8,92 не следует из полученного ряда измерений.КОНТРОЛЬНЫЕ ВОПРОСЫ Что такое генеральная совокупность и выборка изделий? Какие выборочные оценки называются состоятельными, несмещенными и эффективными? Как строится полигон? Как строится гистограмма? Дайте характеристики положения случайных величин. Дайте характеристики рассеяния случайных величин. Сущность гипотезы о равенстве дисперсий. Сущность гипотезы о равенстве средних. Сущность критерия Колмогорова. Что такое критерий Пирсона и для чего он используется? Что понимают под случайными, систематическими и грубыми ошибками? Сущность критерия Романовского. 3.ВЫБОР ПОКАЗАТЕЛЕЙ ДЛЯ ОЦЕНКИ КАЧЕСТВА И НАДЕЖНОСТИ ЭЛЕКТРОННЫХ СРЕДСТВ При оценке качества и надежности ЭС первостепенной задачей является выбор контролируемых показателей. Это обусловлено следующими причинами: 1) часть показателей содержит незначительную информацию о качестве ЭС и характере его изменения во времени; 2) с уменьшением числа показателей упрощается алгоритм принятия решения об уровне качества ЭС и минимизируются материальные и временные затраты. В общем случае задача выбора контролируемых показателей ЭС представляет процедуру упорядочения их в ряд по степени значимости (важности) и исключения последних членов ряда, несущих малую информацию о его качестве. Рассмотрим основные методы выбора единичных показателей для оценки качества и надежности ЭС. 3.1.МЕТОД ЭКСПЕРТНЫХ ОЦЕНОК Экспертный метод отличается от статистических тем, что здесь «датчиком» информации служат эксперты (компетентные специалисты). Для ограничения возможности проявления субъективизма при экспертизе и соответственно повышения ее эффективности предлагается следующая аксиоматика метода. Аксиома 1. Объектом экспертизы служат задачи, которые на данном этапе исследования не могут быть разрешены соответствующими теоретическими или экспериментальными методами. Аксиома 2. Цель экспертизы формулируется в ясной и четкой форме, не допускающей различных толкований. Аксиома 3. К экспертизе должны привлекаться специалисты различных научных школ , технических и производственных направлений при безусловном исключении лиц, субъективно заинтересованных в одностороннем решении вопроса. Аксиома 4. Перед проведением экспертизы эксперту необходимо предоставить всю имеющуюся априорную информацию о качестве изделия на стадиях его проектирования, производства и эксплуатации . Аксиома 5. Ответы экспертов рассматриваются как результаты независимых опытов. В связи с этим положением при проведении экспертизы должны быть исключены возможности общения экспертов между собой в той мере, в какой это может повлиять на независимость опытов. Аксиома 6. Резко выделяющиеся результаты (грубые ошибки) должны быть исключены из множества полученных ответов экспертов. Для этого используется критерий Романовского (см. раздел 2.6). Алгоритм метода 1. Выбор экспертов. Ввиду влияния на ответы экспертов множества случайных причин, результат экспертизы отдельного эксперта по конкретному показателю качества ЭС aji (1 ≤ aji ≤ M; j=1, 2, …, F, F – число экспертов; i=1, 2, …, M – общее число исследуемых показателей) является случайной величиной, колеблющейся около среднего значения mi 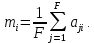 Тогда наименьшая допустимая численность экспертов Fmin в зависимости от вероятности правильного решения задачи P и допустимой погрешности результата экспертизы 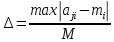 находится из табл.2. находится из табл.2.Таблица 2 Наименьшая допустимая численность экспертов Fmin
На практике обычно задаются величиной P = 0,95 , а значение ∆ выбирается из условия ∆≤0,35. 2. Опрос экспертов. Эксперт наиболее важному показателю качества ЭС ставит ранг 1, второму по важности – 2 и т.д. Наименее важный показатель имеет ранг M. Таким образом происходит ранжировка показателей по натуральному ряду от 1 до M. Когда эксперт считает, что 2 или более показателей имеют одинаковую степень важности, то он им ставит «связанный» ранг, равный среднему значению мест, которые они поделили между собой. Условием правильной ранжировки для j-го эксперта при наличии у него «связанных» рангов является выполнение равенства: 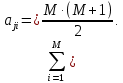 Например, если показатели x1 и x5 при ранжировании по натуральному ряду от 1 до M поделили между собой 3 и 4 места, то им обоим приписывается «связанный» ранг (3 + 4) / 2 = 3,5. 3. Построение матрицы рангов. Результаты опроса F экспертов представляется матрицей рангов с элементами aji, имеющей число строк равное числу экспертов и число столбцов равное числу показателей качества изделия (табл.3). Таблица 3 Матрица рангов показателей качества ЭС
4. Обработка результатов экспертизы: - грубые ошибки экспертов исключаются из рассмотрения на основе критерия Романовского; - определяется сумма рангов hi по каждому показателю 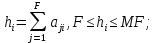 - оценивается степень согласованности мнений экспертов с помощью коэффициента конкордации W (0≤W≤1, W=1 при абсолютном совпадении ответов всех экспертов) по формуле 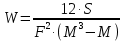 - при отсутствии « связанных» рангов, - при отсутствии « связанных» рангов,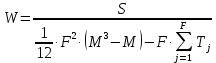 - при наличии «связанных» рангов, - при наличии «связанных» рангов,где 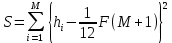 , ,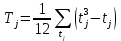 , tj – число одинаковых рангов в j – строке матрицы; , tj – число одинаковых рангов в j – строке матрицы;- оценивается значимость коэффициента конкордации по критерию χ2. Расчетное значение χ2 равно: 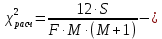 при отсутствии «связанных» рангов; при отсутствии «связанных» рангов;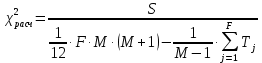 - при наличии «связанных» рангов. - при наличии «связанных» рангов.Коэффициент конкордации W считается статистически значимым, если 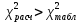 , где , где 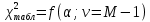 ; ;- при статистической значимости W производится ранжировка показателей качества ЭС по величине hi. Показатель качества ЭС, имеющий минимальное значение hmin, считается наиболее важным, а - hmax – наименее важным; - определяются коэффициенты весомости показателей βi по формуле 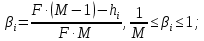 - показатели качества ЭС располагаются в ряд в порядке убывания их коэффициентов весомости, т.е. в порядке убывания их важности. Рассмотренный метод экспертных оценок имеет недостаток – влияние субъективизма на результат экспертизы. Вместе с тем, объективно признается, что при решении многих задач экспертный метод является единственным и эффективным при современном состоянии знаний об объекте эксперимента. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||