Пособие КиНЭС. Министерстерство образования и науки российской федерации
 Скачать 0.95 Mb. Скачать 0.95 Mb.
|
4.6.1. КОНТРОЛЬНЫЙ ЛИСТКонтрольный лист позволяет оценить состояние производства и качество произведенных за день изделий.Для дискретных значений показателя качества ЭС контрольный лист представляет статистический ряд наблюдений. Пример такого статистического ряда измерений приведен в табл. 12. Таблица 12 Пробивное напряжение биэлектрических слоев 160 однотипных МОП-структур
В табл. 12: х- пробивное напряжение; m- частота пробивного напряжения в конкретном интервале (число интервалов – 32). Контрольный лист для непрерывных случайных величин строится аналогично табл. 12 (см. раздел 2.2). 4.6.2. ГРАФИЧЕСКИЕ МЕТОДЫ Графические методы представления статистических данных показателя качества ЭС : 1) полигон ( m/n = Pi=f (x) или mi=f(х)) – для дискретных случайных величин; 2) гистограмма ( m/n = Pi =f (x) или mi=f(х)) – для непрерывных случайных величин; 3) кумулятивная кривая (кумулята) ( 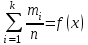 ) )или 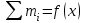 – для дискретных и непрерывных случайных величин. – для дискретных и непрерывных случайных величин.На основе полученных в результате измерения показателя качества значений абсолютных частот mi (или частостей mi/n) подсчитывают накопленные частоты (частости). Накопленная частота (частость) каждого значения показателя качества получается суммированием всех частот (частостей), предшествующим значениям параметра. График накопленных частот представляет кумулятивную кривую. Часто ее называют интегральной кривой. Накопленные частоты (частости) интервального ряда относятся не к серединам интервалов, а к верхним границам каждого из них. Высота последней ординаты соответствует объему наблюдений всего ряда или 100% (рис. 9). Рис.9 построен по данным табл.12. 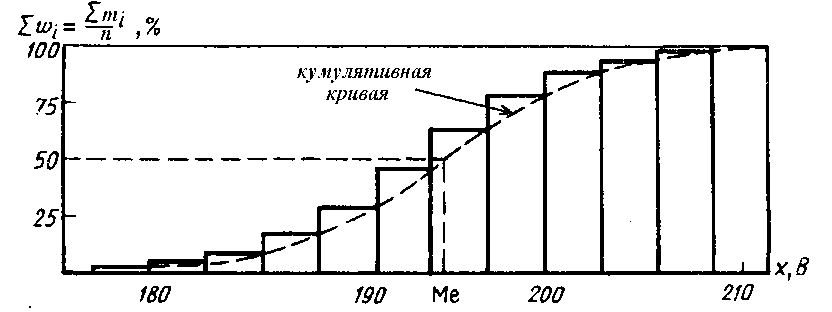 Рис. 9. Кумулятивная кривая Кумулятивная прямая имеет более плавный характер изменения, чем гистограмма или полигон , т.к. накопление приводит к сглаживанию. 4.6.3. ДИАГРАММА РАЗБРОСА ( ПОЛЕ КОРРЕЛЯЦИИ ) Диаграмма разброса применяется для исследования зависимости (корреляции) между двумя видами статистических данных. Поэтому ее часто называют полем корреляции. С помощью диаграммы разброса удобно наблюдать процесс изменения показателя качества ЭС во времени при воздействии тех или иных факторов. Пример. Требуется выяснить влияние термообработки интегральной схемы (ИС) при Т=1200С в течение t=24 ч. на уменьшение обратного тока р-n перехода. Взято 25 ИС и замерены значения Jобр (табл.13), где: x (Jобр при t=0 ч) ; y (Jобр при t=24 ч). Таблица 13 Значение обратного тока до и после обработки интегральных микросхем
Из таблицы имеем: Xmax=92; Ymax=88; Xmin=60; Ymin=57. Наносим на график по оси абсцисс значения Х, по оси ординат - значения Y. При этом длину осей делают почти равной разности между их max и min значениями. На вид график приближается к квадрату. В нашем случае Xmax- Xmin=32; Ymax- Ymin=31; поэтому промежутки между делениями шкалы можно делать одинаковыми. На график наносим данные в порядке измерений и получаем точки диаграммы рассеяния (рис.10). 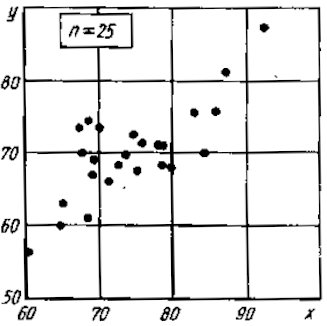 Рис. 10. Диаграмма рассеяния Совокупность точек на графике - диаграмма рассеяния. Если разброс значений исследуемого показателя качества составляет несколько порядков, то удобно применять логарифмический масштаб по осям. Если на одну и ту же точку графика попадает несколько значений показателя качества, то они обозначаются как точка в круге и возле точки проставляется число данных. С помощью диаграммы разброса можно выяснить, имеется ли корреляционная связь между показателями, оценить с помощью коэффициента парной или множественной корреляции степень этой связи и методом наименьших квадратов определить вид этой связи. Примеры корреляционных связей между двумя случайными величинами xи yприведены на рис.11. 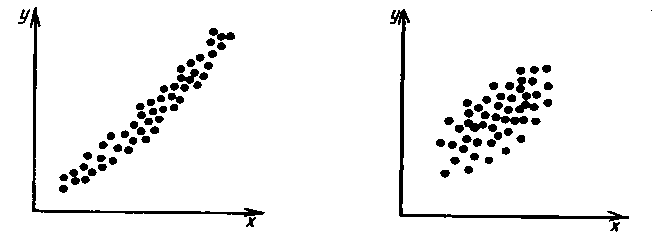 Прямая корреляция Легкая прямая корреляция 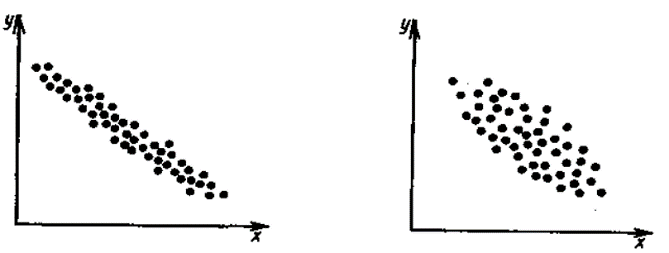 Обратная (отрицательная) Легкая обратная корреляция корреляция 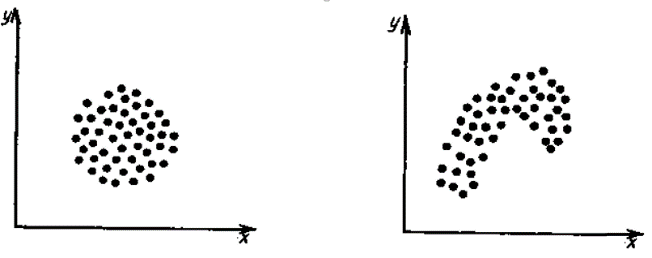 Отсутствие корреляции Криволинейная корреляция Рис.11. Виды корреляционных связей Криволинейную корреляцию можно разделить на участки, имеющие прямолинейный характер, и исследовать каждый участок в отдельности как прямолинейную корреляцию. Степень корреляционной связи случайных величин X и Y может быть оценена: - коэффициентом корреляции (прямолинейная); - корреляционным отношением (криволинейная). Прямолинейную корреляционную связь между показателями Y и X можно найти, используя формулу 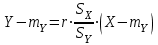 , ,где r - коэффициент парной корреляции 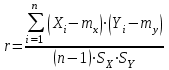 ; ;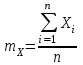 - среднее значение показателя Х; - среднее значение показателя Х;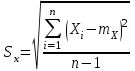 - среднее квадратическое отклонение Х; - среднее квадратическое отклонение Х;n - число пар наблюдений над показателями Х и У. По аналогичным формулам вычисляются среднее значение и среднее квадратическое отклонение для показателя У. Коэффициент парной корреляции находится в пределах: -1 r 1. При r=1 - связь функциональная. Зависимость между X и Y в виде формулы (например, закон Ома, все точные законы механики, физики, химии, астрономии). При r<1 - связь статистическая. Каждому фиксированному значению X соответствует ряд изменяющихся вместе с X значений Y и наоборот. При r = 0 показатели Х и У абсолютно не зависят друг от друга. Показатели X и Y считаются статистически зависимыми с вероятностью Р = 1 - 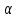 , если выполняется условие: , если выполняется условие: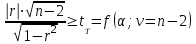 , ,где tT – табличное значение t-статистики Стьюдента [2]. Знак коэффициента корреляции r говорит о следующем: “ – “ X Y и наоборот X Y; “+” X Y и наоборот X Y. 4.6.4. МЕТОДЫ РАССЛАИВАНИЯПростой и эффективный статистический метод, широко используемый в системе управления качеством ЭС – метод расслаивания. Он поставлен на первое место среди семи статистических методов контроля и анализа качества различных изделий.В основе метода - расслаивание статистических данных (т.е. группировка данных) в зависимости от условий их получения и обработка каждой группы в отдельности. Данные, разделенные на группы в соответствии с их особенностями, называют слоями (стратами), а сам процесс разделения на слои (страты) - расслаиванием (стратификацией). Существуют различные разновидности метода расслаивания, применение которых зависит от конкретных задач. В производственных условиях обычно используется метод 4М , учитывающий четыре фактора, зависящие от: человека-исполнителя (man); машины-оборудования (machine); материала-технологии (material); метода-способа производства (method). Расслаивание осуществляется: по исполнителям - квалификации, полу, стажу работы и т.п.; по оборудованию-году выпуска, марке, типу конструкции, выпускающей фирме и т.п.; по технологии- качеству сырья, производственному процессу, фирме-производителю и т.п.; по способу производства – технологическому процессу , масштабу производства и т.п. В результате расслаивания обязательно должны соблюдаться два условия: 1) различия между значениями показателя качества изделия внутри слоя должны быть как можно меньше по сравнению с различием их значений в нерасслоенной исходной совокупности; 2) различие между слоями (различие между средними значениями случайных величин слоев) должно быть как можно больше. Пример. Рассмотрим гистограмму результатов измерения пробивного напряжения полупроводниковых структур (рис.12), изготовленных исполнителем А (левая часть n=75) и B (правая часть n=85), по данным из табл. 12. 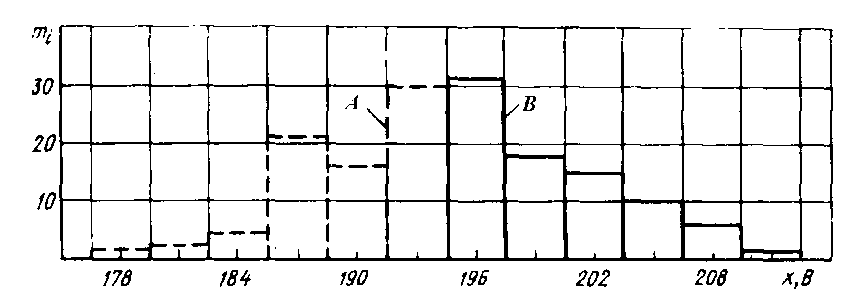 Рис. 12. Гистограмма результатов измерения пробивного напряжения МОП-структуры, изготовленные исполнителем B, более качественные, т.к. имеют большее пробивное U. Результаты исполнителей A и B заметно отличаются друг от друга. Вычислив среднее значение и дисперсию, имеем: mА=189,4 ; SА2=13,2; mВ=199,8; SВ2=14,7. Общее среднее m =194,95 ; общая дисперсия S2=41,2. Результаты показывают, что проведенное расслаивание резко уменьшает дисперсию внутри слоев. При контроле качества изготовления изделий на практике возникает задача предполагаемого источника ухудшения его качества , когда разброс (дисперсия) значений показателя качества около среднего значения возрастает. В случае нормального закона распределения контролируемого показателя качества изделия такую информацию возможно получить путем расслаивания дисперсии с помощью дисперсионного анализа. Общая (суммарная) изменчивость статистических данных, характеризующих качество изделия, состоит из случайной и систематической изменчивости. Источники случайной изменчивости – несоблюдение методик измерения, некачественные исходные материалы, низкая квалификация исполнителей и т.п. Источники постоянной изменчивости – ошибки эталонов, по которым проградуированы измерительные приборы, неучет температурных и др. поправок, изменение условий технологического процесса, параметров технологического оборудования и т.п. При статистическом анализе экспериментальных данных дисперсия внутри выборки Sвн2 характеризуется в основном случайной изменчивостью, а дисперсия между выборками Sср2 - систематической. Сравнивая дисперсию, обусловленную случайным или систематическим фактором, с общей (суммарной) дисперсией, с помощью дисперсионного анализа можно решить вопрос о значимости влияния этого фактора на Sсумм.2. Пример. Имеем 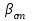 (статистический коэффициент усиления транзисторов по току) для четырех выборок, каждая из которых содержит 5 транзисторов. Выборки взяты из генеральной совокупности, подчиняющейся нормальному закону распределения. Результаты расчетов: (статистический коэффициент усиления транзисторов по току) для четырех выборок, каждая из которых содержит 5 транзисторов. Выборки взяты из генеральной совокупности, подчиняющейся нормальному закону распределения. Результаты расчетов: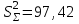 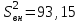 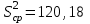 общая; внутри выборок; между выборками. По критерию Фишера: 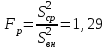 ; ;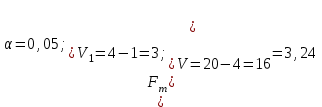 . .Так как Fр < Fт, то в исследуемом технологическом процессе систематические изменения не превалируют и влияние их в общую изменчивость процесса равноценно случайным изменениям (хотя Sср.2 < Sвн.2). Если бы оказалось Fр Fт, то в технологическом процессе превалировала бы систематическая изменчивость. В этом случае источник снижения качества изделия надо искать в технологическом оборудовании. В нашем же примере нет источника, ухудшающего качество изделия, и технологический процесс проходит в соответствии с требованиями нормативно-технической документации. 4.6.5. ДИАГРАММА ПАРЕТО Названа по имени итальянского экономиста Парето (1845 - 1923). Широко применяется как один из семи основных методов контроля качества продукции. Используется при решении следующих задач: появлении некачественных изделий в процессе производства; неисправностях технологического оборудования; увеличении времени от выпуска партии изделия до ее сбыта; наличии на складе нереализованной продукции; поступлении рекламаций от заказчика. Диаграмма Парето позволяет установить основные факторы, которые надо исследовать с целью преодоления возникших проблем. Построение диаграммы Парето начинают с классификации возникающих проблем (например: проблемы, относящиеся к работе оборудования, работе исполнителей и т.д.). Затем производят сбор и анализ статистического материала по каждому фактору, определяющему проблему, для выявления превалирующих. В прямоугольной системе координат по оси абсцисс откладывают равные отрезки, соответствующие рассматриваемым факторам, а по оси ординат - величину их вклада в решаемую проблему. Причем порядок расположения факторов таков, что влияние каждого последующего фактора, расположенного по оси абсцисс, уменьшается по сравнению с предыдущим. В результате получается диаграмма , где число столбцов соответствует числу факторов, а их высота - степени влияния на решаемую проблему. Пример. На рис. 13 приведена гистограмма распределения вклада различных технологических операций в суммарное количество дефектов готовых интегральных схем (ИС). Р 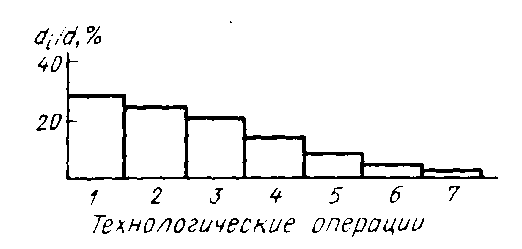 ис. 13. Гистограмма распределения вклада дефектов различных технологических операций в суммарное количество дефектов готовых ИС: 1 - пайка (26%); 2 – герметизация (22%); 3 - разварка выводов (19%); 4 – фотолитография (18%); 5 - осаждение диэлектрика (7%); 6 – диффузия (5%); 7 – металлизация (3%)  Суммируя последовательно высоту всех столбцов гистограммы (рис.13), строим ломаную кумулятивную кривую, которая называется кривой Парето или диаграммой Парето (рис.14). Рис.14.Диаграмма Парето В диаграмме Парето: по оси абсцисс - факторы (технологические операции), при которых появился тот или иной дефект ИС; по оси ординат - относительная доля числа дефектов от рассматриваемого фактора (операции); di - число дефектов от i-й операции; d - общее число дефектов готовых ИС. Из рис. 14 видно, что наибольший процент брака готовой продукции (67%) дают первые три операции, которые представляют собой сборочные операции. Из оставшихся 4 операций главенствующее положение занимает фотолитография (18%), остальные 3 операции - дают в сумме 15% брака. Поэтому, с точки зрения повышения качества ИС, надо проанализировать сборочные операции и операцию фотолитографии. При использовании диаграммы Парето для контроля важнейших факторов наиболее распространенным методом анализа является АВС-анализ (анализ трех основных групп). Сущность АВС-анализа рассмотрим на примере. Пример. На складе скопилось большое количество готовой продукции. Реализация задерживается из-за длительного времени выходного контроля готовых изделий. В результате изготовитель несет большие потери в связи с задержкой поставок. Анализ показал, что изготовитель проводит выходной контроль всех изделий одинаково, без всякого различия в их стоимости. Разделим все изделия, хранящиеся на складе, по группам в зависимости от их стоимости (табл.14). Таблица 14 Складские запасы изделий
Для проведения АВС-анализа построим таблицу с накоплением до 100% (табл.15). Таблица 15 Таблица накопленных процентов
Имея табл.15, строим диаграмму Парето (рис.15). 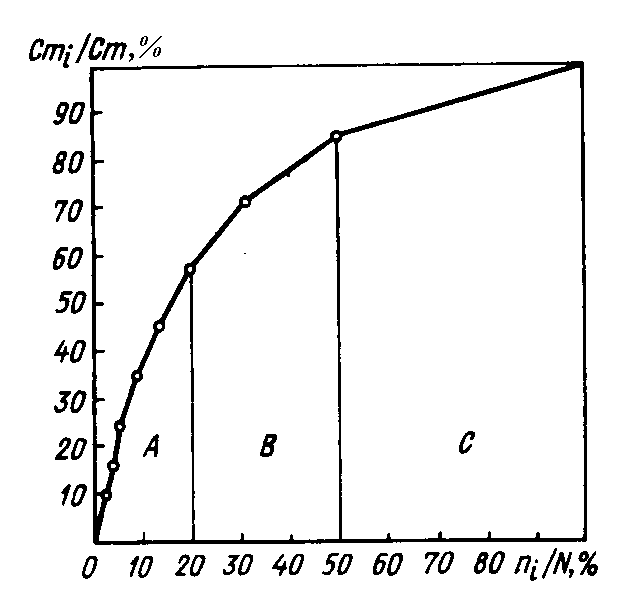 Рис. 15. Диаграмма Парето АВС- анализа Кривая Парето получилась сравнительно плавной из-за наличия большого числа групп. Согласно табл.15 и рис.15: на долю наиболее дорогих изделий (стоимость от 30 тыс. до 100 тыс. р. за одно изделие) первые 7 строк таблицы , составляющих 20% общего числа изделий, приходится 57,0% общей стоимости всей готовой продукции; на долю самых дешевых изделий последняя строка таблицы , составляющих 50% от всего количества изделий на складе, приходится 13,4% от общей стоимости. Назовем группу изделий стоимостью от 30 тыс.р. до 100 тыс.р. группой А; группу самых дешевых изделий до 10 тыс.р. (последняя строка табл.15) ‑ группой С; промежуточную группу, стоимость которой 29,6% (100-57-13,4) (восьмая и девятая строка) ‑ группой В. Данные сведем в табл. 16. Таблица 16 Таблица АВС-анализа складского запаса изделий
Из табл.16 следует, что контроль изделий на складе будет эффективнее в том случае, если контроль изделий группы А будет самым жестким, а контроль изделий группы С ‑ упрощенным. АВС-анализ широко применяется для контроля за производительностью труда, контроля денежных сумм, связанных со сбытом и т.д. Если, например, АВС-анализ применить для случая, изображенного на рис.13, получим: А ‑ сборочные операции; В ‑ фотолитография; С ‑ прочие технологические операции изготовления ИС. 4.6.6. ПРИЧИННО – СЛЕДСТВЕННАЯ ДИАГРАММА Все многообразие факторов и причин, определяющих качество ЭС, можно рассматривать с помощью метода 4М. Зависимость между процессом 4М, представляющим собой систему причинных факторов, и качеством, представляющим собой результат действия этих причинных факторов, имеет вид (рис.16): 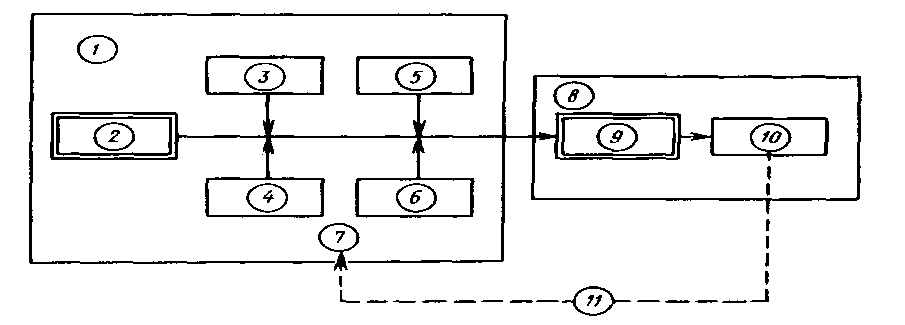 Рис. 16. Причинно-следственная диаграмма: 1 - система причинных факторов; 2 - основные факторы производства; 3 – материал; 4 – человек; 5 – машина; 6 – метод; 7 - процесс 4М; 8 – следствие; 9 – параметры, определяющие качество; 10 - показатели качества; 11 - контроль и управление качеством Если в результате процесса качество изделия неудовлетворительное, то в какой-то точке процесса произошло отклонение от заданных условий. Эту причину необходимо обнаружить и устранить. Для производства качественных изделий необходимо наиболее важным показателям качества (являющимся следствием) поставить в соответствие определенные факторы производства (составляющие систему причинных факторов). При этом важно иметь зависимость между характеристиками качества и параметрами процесса. Показатели качества, являющиеся следствием процесса, имеют всегда разброс значений. Поиск факторов, оказывающих наибольшее влияние на разброс значений показателей качества, называют исследованием причин. Итак, причинно-следственная диаграмма позволяет выявить и систематизировать различные факторы и условия (например, исходные материалы, условия технологической операции, параметры технологического оборудования, исполнители и т.п.), влияющие на показатели качества. Информацией о показателях качества для построения диаграммы служат: журнал регистрации технологической операции; данные текущего контроля; данные испытаний; сообщения производственного персонала и т.д. Сложная причинно-следственная диаграмма анализируется с помощью расслоения по обязательным факторам, таким, как материалы, оборудование, исполнители, время проведения операций и т.п. При значительном разбросе между слоями принимают определенные меры для ликвидации причины его появления. В результате остаются только случайные факторы, уменьшить число которых сложнее, но возможно с помощью причинно-следственной диаграммы. Последовательность ее построения заключается в следующем. Собрать данные, имеющие отношение к браку; выявить количество дефектов; подсчитать сумму потерь от вида дефекта. С помощью диаграммы Парето и АВС-анализа оценить вклад каждого вида дефекта в суммарный брак изделий, определив группы А, В и С видов дефектов. Разбить весь процесс жизненного цикла изделия на основные этапы, влияющие на появление групп дефектов А и В. Построить причинно-следственную диаграмму выбранных групп дефектов. Рассортировать причины на устранимые, трудноустранимые и неустранимые. Подготовить и реализовать план мероприятий по исключению устранимых и уменьшению влияния трудноустранимых причин. Собрать данные (за срок после выполнения плана мероприятий), имеющие отношение к браку изделий; выявить количество дефектов, отнесенных ранее к группам А и В; подсчитать сумму потерь от каждого вида дефекта. Построить вновь диаграмму Парето и проверить эффективность проведенных работ. 4.6.7. СТАТИСТИЧЕСКИЙ КОНТРОЛЬ КАЧЕСТВА ЭЛЕКТРОННЫХ СРЕДСТВ НА ОСНОВЕ КОНТРОЛЬНЫХ КАРТ 4.6.7.1. ВИДЫ СТАТИСТИЧЕСКОГО КОНТРОЛЯ Статистический контроль - это процесс установления соответствия между состоянием изделия и заданными на него нормами. В зависимости от стадии “жизни” изделия различают производственный и эксплуатационный контроль. Производственный контроль, т.е. статистический контроль на стадии технологического процесса производства, охватывает все вспомогательные, подготовительные и технологические операции. В зависимости от места в цепи технологического процесса производственный контроль подразделяют на входной, операционный и приемочный. Входной контроль - контроль продукции поставщика, поступившей к заказчику и предназначенной для использования при изготовлении, ремонте или эксплуатации ЭС. Материалы, полуфабрикаты, комплектующие изделия подвергаются входному контролю на соответствие требованиям нормативно-технической документации. Операционный контроль - контроль изделия после завершения определенной операции. Приемочный контроль - контроль готового изделия по окончании всех технологических операций. Эксплуатационный контроль - контроль, осуществляемый на стадии эксплуатации ЭС. Статистический контроль в основном базируется на контроле измеренных значений показателей качества изделия и сравнении их значений с заданными по нормативно-технической документации. Поэтому он часто называется параметрическим контролем. Перечисленные виды контроля могут быть сплошными (100%) и выборочными. Контроль по количественному признаку - регистрация числовых значений измеряемых показателей качества изделия. Контроль по качественному признаку - выделяются категории, к которым принадлежат контролируемые изделия. Частным случаем контроля по качественному признаку является контроль по альтернативному признаку - когда производится разбиение изделий на качественную и некачественную продукцию. Летучий контроль - выборки для контроля берутся из партии изготавливаемых изделий в случайное время. 4.6.7.2. КОНТРОЛЬНАЯ КАРТА ДЛЯ СРЕДНИХ ЗНАЧЕНИЙ Контрольная карта позволяет осуществить непосредственное регулирование технологического процесса и контроль качества изделия. Контрольная карта графически представляет собой три линии (рис 17). 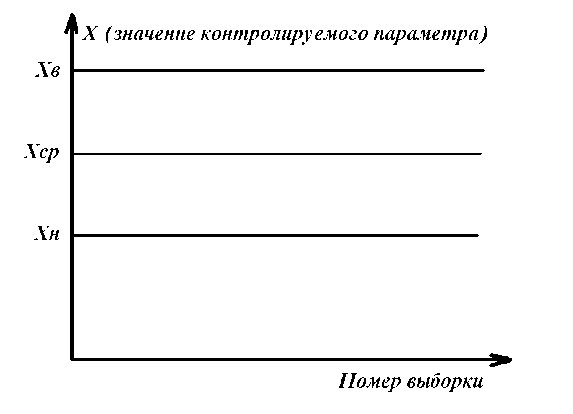 Рис. 17. Общий вид контрольной карты При построении контрольной карты главным является правильный выбор нижней Хн и верхней Хв границ допустимого изменения контролируемого показателя качества ЭС (границ регулирования для контрольной карты). При нормальном законе распределения в пределах 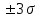 находится 99,73% всех значений контролируемого показателя качества. Отсюда следует, что почти все средние, вычисленные по результатам выборок из генеральной совокупности с математическим ожиданием М(х) и средним квадратическим отклонением , приходятся на участок с границами находится 99,73% всех значений контролируемого показателя качества. Отсюда следует, что почти все средние, вычисленные по результатам выборок из генеральной совокупности с математическим ожиданием М(х) и средним квадратическим отклонением , приходятся на участок с границами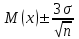 . .Эти две границы называют границами регулирования контрольной карты для средних 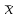 (х-карты): (х-карты):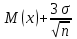 ‑ верхняя граница (уровень) регулирования; ‑ верхняя граница (уровень) регулирования;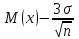 ‑ нижняя граница (уровень) регулирования. ‑ нижняя граница (уровень) регулирования.Существуют три варианта оценки качества изготовления изделия: по измеряемым показателям качества (физические, электрические , механические характеристики и др.); по доле бракованных изделий в %; по числу дефектов (по контролируемым показателям) на единицу продукции. Вычисление границ регулирования для 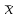 -карты. -карты.Если известны М(х) и , то верхняя и нижняя границы для 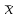 -карты равны: -карты равны: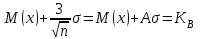 ; ;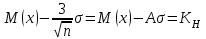 ; ;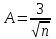 ‑ коэффициент. ‑ коэффициент.Если М(х) и неизвестны, то берут выборочные оценки m(x) и S. 4.6.7.3. S – КАРТА И R - КАРТА Чтобы получить более точное представление о ходе технологического процесса, наряду с 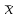 -картой ведут либо S-карту, с помощью которой непрерывно контролируют среднее квадратическое отклонение, либо R-карту для контроля размахов выборок. При этом создание контрольной карты обычно начинают с изготовления карт для среднего квадратического отклонения или размахов, а не с карты для средних значений, так как к моменту начала контроля производства имеется мало исходных данных для оценки М(х) и, следовательно, для создания карты средних значений. -картой ведут либо S-карту, с помощью которой непрерывно контролируют среднее квадратическое отклонение, либо R-карту для контроля размахов выборок. При этом создание контрольной карты обычно начинают с изготовления карт для среднего квадратического отклонения или размахов, а не с карты для средних значений, так как к моменту начала контроля производства имеется мало исходных данных для оценки М(х) и, следовательно, для создания карты средних значений.Построение S-карты и R-карты аналогично карте средних значений [10, с.184-186]. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
