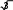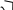39
j20 2.74ej100451 A
j13
I3 I1 Z
Z2
2 Z3
4.5e j230551
24
39
j7 j13
2.74e j580351 A
Токи İ2 и İ3 можно найти и по другому:
U Z I I
Z2 Z3
4.5e j230551 (24
j7)(15
j20) 68.4e j50301 B
bc bc1
Z
2
3
1 Z
39 j13
I Ubc
68.4
j50301
2.74ej100451 А
Z
2
2 25e j160151
j50301
3
I Ubc
Z3
68.4
25e j530051
2.74e j580351 А
Найдем мощности всей цепи и отдельных ее ветвей: Š=ÚÏ =120 4,5ej230 551 540ej230 551 BAДля определения активной и реактивной мощностей полную мощность, выраженную комплексным числом в показательной форме, переводим в алгебраическую форму. Тогда действительна часть комплекса будет представлять собой активную мощность, а мни мая—реактивную: Š =540 соs 23° 55’ +j540sin 23° 55’ —494 + j218 ВA откуда
Р=494 Вт; Q=218 BAр.
Активную и реактивную мощности можно найти и по-другому:
1
P ReUI Re120 4.5ej230551 120 4.5cos 230551 494 Bm
P rI2 10 4.52 202 Bm P rI2 180 Bm
1 1 1 2 2 2
P rI2180 Bm
3 3 3
Проверка показывает, что Р = Р1 +Р2 +Р3
1
Q ImUI Im120 4.5ej230551 120 4.5sin 230551 218
BAp
Q xI2 6 4.52 122 BAp Q xI2 52.5 BAp
1 1 1 2 2 2
Q xI2 150
BAp
3 3 3
Учитывая, Q1 и Q3 что положительны (реактивная мощность индук тивных катушек), а Q2 отрицательно (реактивная мощность конденсатора), получим Q1=Q1 -Q2 +Q3=218 ВАр
На рис. 15 приведена векторная диаграмма токов и напряжений построенная по расчетным данным. Порядок ее построения следующий: по результатам расчетов отложены векторы токов İ1 İ2 и İ3, затем по направлению İ1 отложен вектор r1 İ1 перпендикулярно к нему в сторону опережения — вектор j x1 İ1. Их сумма дает вектор Z1 İ1. Далее в фазе с İ2 построен вектор r2 İ2 перпендикулярно к нему в сторону отставания вектор jx2İ2 а их сумма дает вектор напряжения на параллельном участке Úbc. Тот же вектор может быть получен, если в фазе с İ3 отложить r3 İ3 и к нему прибавить вектор ‚ j x3 İ3, опережаюiций İ3 на 90°. Сумма векторов Z1 İ1 и Úbc дает вектор приложенного напряжения Ú.
Задача 2. Определить эквивалентное комплексное сопротивление, цепи (рис. 16,а), ток и напряжение между точками а и b, с и d,
если U =130 В, r1 =2 Ом, r2 =3 Ом, ωL1=3 Ом, ωL2= 7 Ом, ωM2= 1 Ом.
Ре шен и е. Из рис. 16, а следует, что при заданном направлении тока в каждой катушке потоки самоиндукции и взаимной индукции одинаково направлены. Следовательно, катушки включены согласно. Заданная цепь может быть представлена схемой замещения, показанной на рис. 16,б. Составим для нее уравнение по второму закону Кирхгофа:
Ú= r1 İ + jωL1 İ + jωM İ+ r2 İ+ jωL2 İ+ jωM İ. Эквивалентное комплексное соцротивление цепи
Z= r1
+ jωL1
+ r2
+ jωL2
+2 jωM =5 j12=13ej670201 Ом
Искомый ток
İ=Ú/Z= 130/13ej670201 =10e j670201 А
Комплексные напряжения между точками a и b, c и d равны:
UabUcd (r1 (r2 jM)I (2 j4) 10e j670 201 jM)I (3 j8) 10e j670 201 44.7e j30 501 B 85.5ej20 051 B
На рис.- 16, в представлена векторная диаграмма. По действительной оси отложен вектор напряжения, от него в сторону отставания на 67°201 направлен вектор тока, затем отложены векторы падения напряжения в каждой из катушек.
ТРЕХФАЗНЫЕ ЦЕПИ
При изучении трехфазных цепей особое внимание необходимо обратить на преимущества, которые дает трехфазная система по сравнению с однофазной. Рассматривая схемы соединения обмоток генераторов, надо уяснить связь между фазными и линейными напряжениями в схеме соединения звездой, а также связь между фазными и линейными токами в схеме соединения треугольником.
Необходимо четко представить, что в трехфазной цепи могут быть два режима: симметричный и несимметричный. Расчет трехфазной цепи в симметричном режиме сводится к расчету для одной фазы и производится аналогично расчету обычной цепи однофазного тока. Трехфазная цепь может рассматриваться как разветвленная цепь с тремя источниками питания и для ее расчета применяются методы, используемые при расчете сложных электрических цепей. Например, если несимметричный приемник соединен звездой без нейтрального провода, то для расчета трехфазной цепи можно применить метод узлового напряжения в комплексной форме.
После изучения настоящего раздела студенты должны:
знать основные элементы трехфазных цепей, способы соединения фаз обмотки генератора и включения в трехфазную цепь приемников; способы изображения трехфазной симметричной системы э. д. с.;
понимать роль нейтрального провода; принципы построения потенциальных диаграмм; влияние рода и схемы включения нагрузки на величину тока, в нейтральном проводе; схемы электроснабжения предприятий;
уметь анализировать различные режимы симметричных и несимметричных цепей; читать схемы соединения трехфазных, и однофазных приемников; предвидеть последствия коммутационных измемений в цепи на ее электрическое состояние.
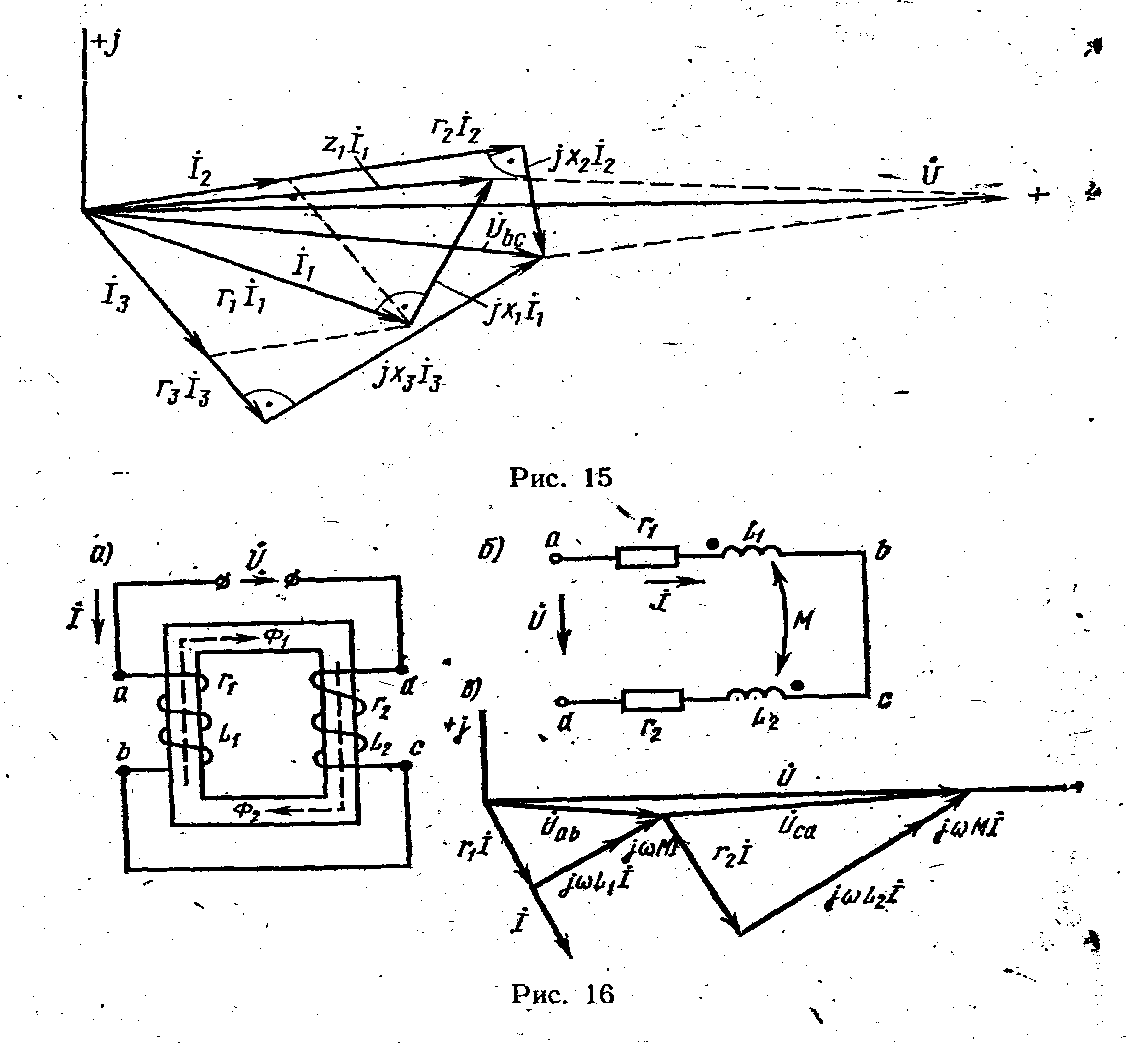
Задача 1. В трехфазную сеть с линейным напряжением Uл =220 В включен приемник, соединенный треугольником, сопротивление каждой фазы которого Z= (10+j10) Ом (рис. 17). Найти токи в каждой фазе нагрузки и линии и показания каждого ваттметра. Построить векторную диаграмму. Найти те же величины в случае обрыва цепи в точке .
Р е ш е н и е. Расчет токов в трехфазных цепях производится комплексным методом. Примем, что вектор линейного напряжения ÚAB направлен по действительной оси, тогда
0
ÚAB = Úab= 220 В; ÚBC = Úbc= 220e j120 В;
CA ca
Ú = Ú = 220ej1200 В .
Определяем фазные токи:
Iab
Uab
Z
220
10 j10
j1200
15.6e j450
11 j11 A;
I Ubc 220e
15.6e j1650
15 j4.03 A;
bc
Ica
Z
Uca
Z
10 j10
220ej1200
10 j10
15.6ej750
4.03 j15 A.
Находим линейные токи:
IA Iab Ica
6.97
j26 26.9e j750 A
bc ab
B
I I I 26 j6.97 26.9ej1650 A
ca bc
C
I I I 19 j19 26.9ej450 A
Определяем показание ваттметров
A
P1 ReUAB
I Re220 26.9ej750 220 26.9cos 750
1530 Bm
P2 ReU
CBIC
Re 220e j1200 26.9e j450 Re220ej600 26.9e j450
220 26.9cos15 0 5730 Bm Активная мощность цепи (алгебраическая сумма показаний ваттметров) Р равна: Р = Р 1 + Р 2 = 1530 + 5730 = 7260 Вт,
ф
 или  P P 3UЛIЛcos 220 26.9cos 450 3rI2 7260 Bm
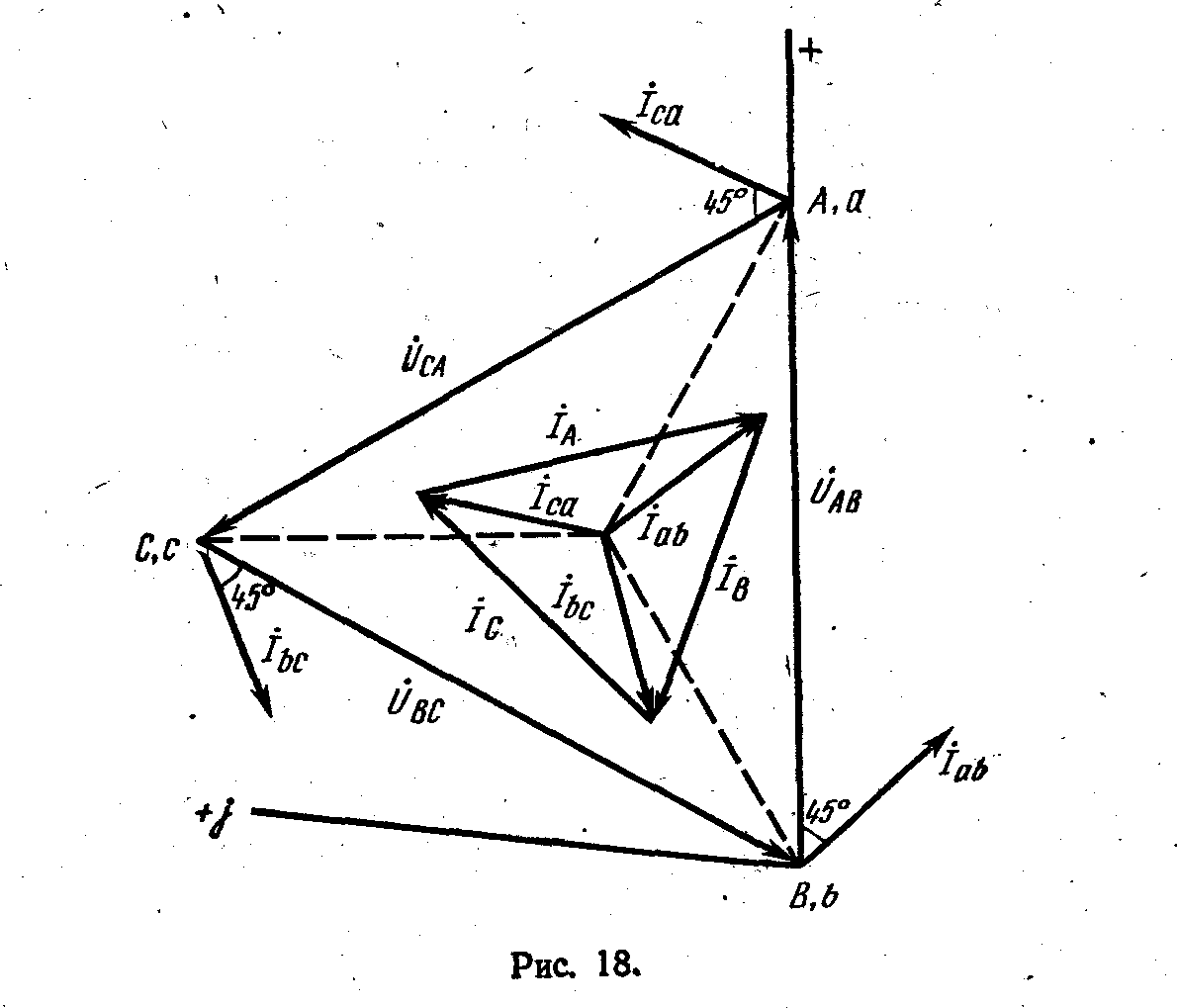
На рис. 18 приводится векторная диаграмма напряжений и токов. При обрыве в точке d токи в фазах нагрузки будут:
I
Ubc
bc
220e j1200
15
j4.03 A;
Z 10
j10
|
 Скачать 0.82 Mb.
Скачать 0.82 Mb.