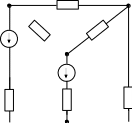
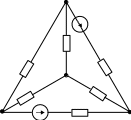
Вариант 17 надо выполнить. 1-2-3-4 РГР247. Министерство высшего и среднего специального образования республики узбекистан

• Название: Министерство высшего и среднего специального образования республики узбекистан
• Анкор: Вариант 17 надо выполнить
• Дата: 19.10.2021
• Размер: 0.82 Mb.
• Имя файла: 1-2-3-4 РГР247.docx
• Тип: Документы; #250591
• страница: 26 из 28

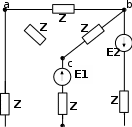
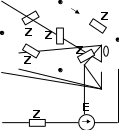
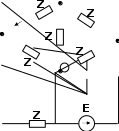
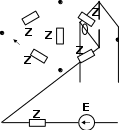
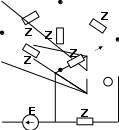
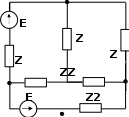
Z

_E1 ^Z Z

c

b a b

Z

_E2 ^Z Z

E_1c

_Z Z Z

E₂

_{Z Z} Z

dРис-1

dРис-2

b

E

Z

Z Z

^{Z d} Z^E Z

a c

dРис-3

b

E

Z

Z

Z
^{Z d} Z

Z _E

a c

Рис-4
b

E

Z

Z _E Z

^{Z d} ZZ

a c

Рис-5 Рис-6
b b

Z

Z

Z

E

^{Z d} Z

Z _E

a c

Z

Z Z

^{Z d} Z

E Z E

a c

Рис-7 Рис-8

b

E _a

Z

Z Z

Z

^d Z

E _Z

a c

Рис-9

Рис-10

_a a

Рис-11


a

Рис-12

Рис-14

Рис-13

Рис-15 Рис-16




Рис-18

Рис-17

ЗАДАНИЕ 4

Для электрической схемы изображенной на рис.3.1-3.17, по заданным в табл. 3 параметрам и линейному напряжению определить фазные и линейные токи в нейтральном проводе (для четырех проводной схемы), активную мощность всей цепи и каждой фазы отдельно. Построить векторную диаграмму токов и напряжений на комплексной плоскости.

Рис. 3-1

Рис.3-2

Рис. 3-3 Рис. 3-4

Рис. 3-5 Рис.3-6

Рис. 3-7

Рис.3-8

Рис. 3-9

Рис.3-10

Рис. 3-11 Рис. 3-12

Рис. 3-13 Рис. 3-14

Рис. 3-15 Рис. 3-16

r_b

Рис.3-17
Контрольная работа №3

Варианты для расчета линейных электрических цепей трехфазного переменного тока для самостоятельных работ

Таблица 3

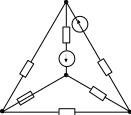
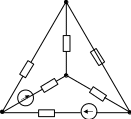
Ва р	Рис	UЛ B	RA О м	RВ Ом	RС Ом	xА Ом	xВ Ом	xС Ом	rАВ Ом	rВС Ом	rСА Ом	xАВ Ом	xВС Ом	xСА Ом
0	3-1	127	8	8	8	6	6	6	-	-	-	-	-	-
1	3-1	220	8	8	8	6	6	6	-	-	-	-	-	-
2	3-1	380	8	8	8	6	6	6	-	-	-	-	-	-
3	3-2	127	3	4	6	4	3	8	-	-	-	-	-	-
4	3-2	220	8	4	6	4	3	8	-	-	-	-	-	-
5	3-2	380	8	4	6	4	3	8	-	-	-	-	-	-
6	3-3	127	4	8	6	3	4	8	-	-	-	-	-	-
7	3-3	220	4	8	6	3	4	9	-	-	-	-	-	-
8	3-3	380	4	3	6	8	4	8	-	-	-		-	-
9	3-4	127	16 .8	8	8	14,2	6	4	-	-	-	-	-	-
10	3-4	220	16 .8	8	8	14,2	6	4	-	-	-	-	-	-
11	3-4	380	16 .8	8	8	8	6	4	-	-	-	-	-	-
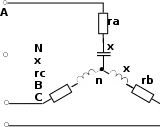
12	3-5	127	10	-	-	-	10	10	-	-	-	-	-	-
13	3-5	220	10	-	-	-	10	10	-	-	-	-	-	-
14	3-5	380	10	-	-	-	10	10	-	-	-	-	-	-
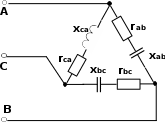
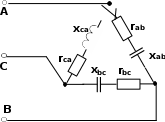
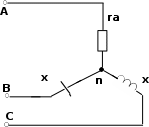
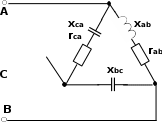
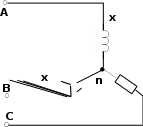
15	3-6	127	-	-	-	-	-	-	8	8	8	6	6	6
16	3-6	220	-	-	-	-	-	-	8	8	8	6	6	6
17	3-6	380	-	-	-	-	-	-	8	8	8	6	6	6
18	3-7	127	-	-	-	-	-	-	8	4	6	4	3	8
19	3-7	220	-	-	-	-	-	-	8	4	6	4	3	8
20	3-7	380	-	-	-	-	-	-	8	4	6	4	3	8
21	3-8	127	-	-	-	-	-	-	4	8	6	3	4	8
22	3-8	220	-	-	-	-	-	-	4	8	6	3	4	8
23	3-8	380	-	-	-	-	-	-	4	8	6	3	4	8
24	3-9	127	-	-	-	-	-	-	16,8	8	3	14,2	6	4
25	3-9	220	-	-	-	-	-	-	16,8	8	3	14,2	6	4

Продолжение табл. 3

Ва р	Рис	UЛ B	RA Ом	RВ Ом	RС Ом	xА О м	xВ Ом	xС Ом	rАВ Ом	rВС Ом	rСА Ом	xАВ Ом	xВС Ом	xСА Ом
26	3-9	380	-	-	-	-	-	-	16,8	8	8	14,2	6	4
27	3- 10	127	-	-	-	-	-	-	10	-	-	-	10	10
28	3- 10	220	-	-	-	-	-	-	10	-	-	-	10	10
29	3- 10	380	-	-	-	-	-	-	10	-	-	-	10	10
30	3- 11	127	10	-	-	-	10	10	-	-	-	-	-	-
31	3- 11	220	10	-	-	-	10	10	-	-	-	-	-	-
32	3- 11	380	10	-	-	-	10	10	-	-	-	-	-	-
33	3- 12	127	15	-	-	-	5	5	-	-	-	-	-	-
34	3- 12	220	15	-	-	-	5	5	-	-	-	-	-	-
35	3- 12	380	15	-	-	-	5	5	-	-	-	-	-	-
36	3- 13	127	-	-	-	-	-	-	-	3	8	4	6	8
37	3- 13	220	-	-	-	-	-	-	-	3	8	4	6	8
38	3- 13	380	-	-	-	-	-	-	-	3	8	4	6	8
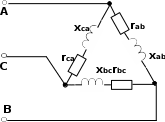
39	3- 14	127	-	-	-	-	-	-	8	4	8	-	6	10
40	3- 14	220	-	-	-	-	-	-	8	4	8	-	6	10
41	3- 14	380	-	-	-	-	-	-	8	4	8	-	6	10
42	3- 15	127	-	-	-	-	-	-	-	5	6	5	8	4
43	3-	220	-	-	-	-	-	-	-	5	6	5	8	4

	15
44	3- 15	380	-	-	-	-	-	-	-	5	6	5	3	4
45	3- 16	127	-	-	-	-	-	-	5	-	6	10	8	4
46	3- 16	220	-	-	-	-	-	-	5	-	6	10	8	4
47	3- 16	380	-	-	-	-	-	-	5	-	6	10	8	4
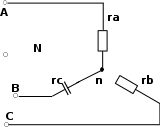
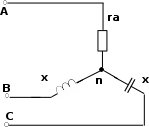
48	3- 17	127	-	3	-	15	-	10	-	-	-	-	-	-
49	3- 17	220	-	3	-	15	-	10	-	-	-	-	-	-
50	3- 17	380	-	3	-	15	-	10	-	-	-	-	-	-

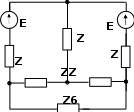
Задача 1. Рассчитать электрическую цепь синусоидального тока со смешанным соединением приемников.

Для схемы, изображенной ва рис. 13, г (на рис. 13, г ток i₂ направлен по часовой стрелке, ток i₃- против часовой стрелки), известно, что

U = 120 В r₁ = 10 Ом r₂ = 24 Ом r₃ = 15 Ом L₁ = 19,1 мГ L₁ = 63,5 мГ C₂ = 455 мкФ f = 50 Гц

Определить токи İ₁ İ₂ İ₃ в ветвях цепи, напряжения на участках цепи Ú_ab Ú_bc активную, реактивную и полную мощности и построить векторную диаграмму.

Р е ш е н и е. Выражаем сопротивления ветвей цепи в комплексной

Z r jx ze^{ j}

форме:

Z₁

 r₁

• 
  jL₁
  

 10  j2  50 19.110^3  10  j6 Ом

Переходя от алгебраической формы записи комплексного числа к

показательной, получаем:

Z ze^j1

1

1
6

 11.6e^j310

tg ^L1


r

1
1

Z₂  r₂

1




2
^jC

 24  j

10


2  50  455

 24  j7  25e^{ j16}0¹⁵1 Ом

Z₃  r₃

• 
  jL₃
  

 15  j2  50  63.5 10^3  15  j20  25e^j530051 Ом

Выражаем заданное напряжение U в комплексной форме. Если начальная фаза напряжения не задана, то ее можно принять равной нулю и располагать вектор напряжения совападающим с положительным и

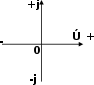Рис.14

направлением действительной оси. В этом случае мнимая составляющая комплексного числа будет отсутст вовать (рис. 14):

Полное комплексное сопротивление цепи

1
Z Z

Z₂ Z<sub>3

 10  j6 </sub> (24  j7)(15  j20) _

Z₂  Z₃

39  j13

10  j6  ^25e

 j16⁰15¹

 25e

53⁰10¹

 24.4  j10.8  26.7e^j230⁵⁵1 Ом

_41ej18⁰25¹

Определяем ток İ₁ в неразветвленной части цепи:

I  ^U

1 <sub>Z

</sub> 120

_26.7ej23⁰55¹

_{ 4.5e} j23⁰55¹ _А

Токи İ₂ и İ₃ в параллельных ветвях могут быть выражены через ток в неразветвленной части цепи:

Z
I₂  I₁

2

Z₃

• 
  Z₃
  

_{ 4.5e} j23⁰55¹ _ ^{15 }