Методы математической обработки данных педагогического исследования. мат пдф (1). Монография Чебоксары 2019 удк 796799 ббк 75. 1 К72 Рецензенты др экон наук, профессор

• Название: Монография Чебоксары 2019 удк 796799 ббк 75. 1 К72 Рецензенты др экон наук, профессор
• Анкор: Методы математической обработки данных педагогического исследования
• Дата: 23.06.2022
• Размер: 0.59 Mb.
• Имя файла: мат пдф (1).docx
• Тип: Монография; #612510
• страница: 19 из 37

Корреляционный анализ

Видывзаимосвязеймеждупризнаками.

Еще Гиппократ обратил внимание на то, что между телосложением и темпераментом людей, между строением их тела и предрасположенно- стью к заболеваниям существует определенная связь.

В предыдущих главах были рассмотрены простейшие ситуации, когда в ходе исследования измерялись значения только одного варьирующего признака генеральной совокупности. Остальные признаки либо считались постоянными для данной совокупности, либо относились к случайным факторам, определяющим варьирование исследуемого признака. Как пра- вило, исследования в спорте значительно сложнее и носят комплексный характер. Например, при контроле за ходом тренировочного процесса из- меряется спортивный результат, и одновременно может оцениваться це- лый ряд биомеханических, физиологических, биохимических и других параметров (скорость и ускорения общего центра масс и отдельных зве- ньев тела, углы в суставах, сила мышц, показатели систем дыхания и кро- вообращения, объем физической нагрузки и энергозатраты организма на ее выполнение и т. д.).

При этом часто возникает вопрос о взаимосвязи отдельных признаков. Например, как зависит спортивный результат от некоторых элементов техники спортивных движений? как связаны энергозатраты организма с объемом физической нагрузки определенного вида? насколько точно по результатам выполнения некоторых стандартных упражнений можно су- дить о потенциальных возможностях человека в конкретном виде спор- тивной деятельности? и т. п. Во всех этих случаях внимание исследова- теля привлекает зависимость между различными величинами, описываю- щими интересующие его признаки.

Этой цели служит математическое понятие функции, имеющее в виду случаи, когда определенному значению одной (независимой) переменной Х,называемой аргументом,соответствует определенное значение другой (зависимой) переменной Y, называемой функцией. Однозначная зависи- мость между переменными величинами Y и X называется функциональ-ной,т.е. Y = f(X) (“игрек есть функция от икс”).

Например, в функции Y = 0,5X каждому значению Y соответствует в два раза большее значение X. Такого вида функциональная зависимость между можностью первой и второй нагрузок и ЧСС представлена при гра- фическом способе определения PWC₁₇₀в велоэргометрической пробе (рис. 2.3.1). Если же в функции Y = —2(X + a)², то каждому значению Yсоответствует 2 строго определенных значения X. В биохимии этот вид функциональной зависимости выявлен между активностью ферментов и рH-среды (рис. 2.3.2).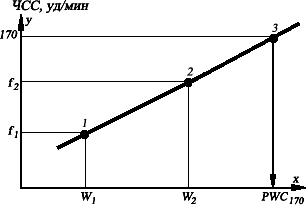


Рис. 2.3.1. Графический способ определения PWC₁₇₀: f₁ и f₂ –

ЧСС при первой и второй нагрузках; W₁ и W₂ –

мощность первой и второй нагрузок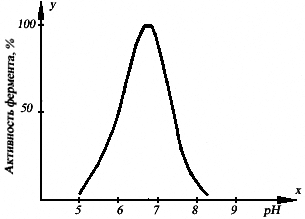




Рис. 2.3.2. Влияние pH-среды на активность ферментов

Но такого рода однозначные или функциональные связи между пере- менными величинами встречаются не всегда. Известно, например, что между ростом (длиной тела) и массой человека существует положитель- ная связь: более высокие индивиды имеют обычно и большую массу, чем индивиды низкого роста. То же наблюдается и в отношении качественных признаков: блондины, как правило, имеют голубые, а брюнеты – карие глаза. Однако из этого правила имеются исключения, когда сравнительно низкорослые индивиды оказываются тяжелее высокорослых, и среди населения хотя и нечасто, но встречаются кареглазые блондины и голубо- глазые брюнеты.

Причина таких “исключений” в том, что каждый биологический при- знак, выражаясь математическим языком, является функцией многих пе- ременных; на его величине сказывается влияние и генетических и средо- вых факторов, в том числе и случайных, что вызывает варьирование при- знаков. Отсюда зависимость между ними приобретает не функциональ-

ный, а статистический характер, когда определенному значению од- ного признака, рассматриваемого в качестве независимой переменной, со- ответствует не одно и то же числовое значение, а целая гамма распреде- ляемых в вариационный ряд числовых значений другого признака, рас- сматриваемого в качестве независимой переменной. Такого рода зависи- мость между переменными величинами называется корреляционной или корреляцией(термин “корреляция” происходит от лат. correlatio– соотно- шение, связь). При этом данный вид взаимосвязи между признаками про-являетсявтом,чтоприизмененииоднойизвеличинизменяетсясреднеезначениедругой.

Если функциональные связи одинаково легко обнаружить и на еди- ничных, и на групповых объектах, то этого нельзя сказать о связях корре- ляционных, которые изучаются только на групповых объектах методами математической статистики.

Задача корреляционного анализа сводится к установлению направле- ния и формы связи между признаками, измерению ее тесноты и к оценке достоверности выборочных показателей корреляции.

Корреляционная связь между признаками может быть линейнойикри-волинейной(нелинейной),положительнойиотрицательной.

Прямая корреляция отражает однотипность в изменении признаков: с увеличением значений первого признака увеличиваются значения и дру- гого, или с уменьшением первого уменьшается второй.

Обратная корреляция указывает на увеличение первого признака при уменьшении второго или уменьшение первого признака при увеличении второго.

Например, более дальний прыжок и большее количество тренировок – прямая корреляция, уменьшение времени, затраченного на преодоление дистанции, и большее количество тренировок – обратная корреляция.

Корреляционныеполяицельихпостроения.

Корреляция изучается на основании экспериментальных данных, представляющих собой измеренные значения (x_i, y_i) двух признаков. Если экспериментальных данных немного, то двумерное эмпирическое распре- деление представляется в виде двойного ряда значений x_iи у_i. При этом корреляционную зависимость между признаками можно описывать раз- ными способами. Соответствие между аргументом и функцией может быть задано таблицей, формулой, графиком и т. д.

Корреляционный анализ, как и другие статистические методы, осно- ван на использовании вероятностных моделей, описывающих поведение исследуемых признаков в некоторой генеральной совокупности, из кото- рой получены экспериментальные значения x_iи у_i.

Когда исследуется корреляция между количественными признаками, значения которых можно точно измерить в единицах метрических шкал (метры, секунды, килограммы и т.д.), то очень часто принимается модель двумерной нормально распределенной генеральной совокупности. Такая модель отображает зависимость между переменными величинами x_iи у_iграфически в виде геометрического места точек в системе прямоугольных

координат. Эту графическую зависимость называются также диаграммойрассеиванияили корреляционнымполем.

Данная модель двумерного нормального распределения (корреляци- онное поле) позволяет дать наглядную графическую интерпретацию ко- эффициента корреляции, т.к. распределение в совокупности зависит от пяти параметров: μ_x, μ_y– средние значения (математические ожидания); σ_x, σ_y – стандартные отклонения случайных величин Х и Y и р – коэффи- циент корреляции, который является мерой связи между случайными ве- личинами Х и Y.

Если  = 0, то значения x_iи y_i, полученные из двумерной нормальной совокупности, располагаются на графике в координатах х, у в пределах области, ограниченной окружностью (рис. 2.3.3, а). В этом случае между случайными величинами Хи Yотсутствует корреляция и они называются некоррелированными. Для двумерного нормального распределения не- коррелированность означает одновременно и независимость случайных величин Х и Y.

Если  = 1 или  = –1, то между случайными величинами Х и Y суще- ствует линейная функциональная зависимость (Y = c+ dX). В этом случае говорят о полной корреляции. При  = 1 значения x_iи y_iопределяют точки, лежащие на прямой линии, имеющей положительный наклон (с увеличе- нием x_iзначения y_iтакже увеличиваются), при  = –1 прямая имеет отри- цательный наклон (рис. 2.3.3, б).

В промежуточных случаях (–1 <  < 1) точки, соответствующие значе- ниям x_i, y_iпопадают в область, ограниченную некоторым эллипсом (рис. 2.3.3, в. г), причем при  > 0 имеет место положительная корреляция (с увеличением x_iзначения y_iимеют тенденцию к возрастанию), при  < 0 корреляция отрицательная. Чем ближе  к 1, тем уже эллипс и тем теснее экспериментальные значения группируются около прямой линии.

Здесь же следует обратить внимание на то, что линия, вдоль которой группируются точки, может быть не только прямой, а иметь любую дру- гую форму: парабола, гипербола и т. д. В этих случаях мы рассматривали бы так называемую, нелинейную (или криволинейную) корреляцию (рис. 2.3.3, д).

Таким образом, визуальный анализ корреляционного поля помогает выявить не только наличия статистической зависимости (линейную или нелинейную) между исследуемыми признаками, но и ее тесноту и форму. Это имеет существенное значение для следующего шага в анализе – вы- бора и вычисления соответствующего коэффициента корреляции.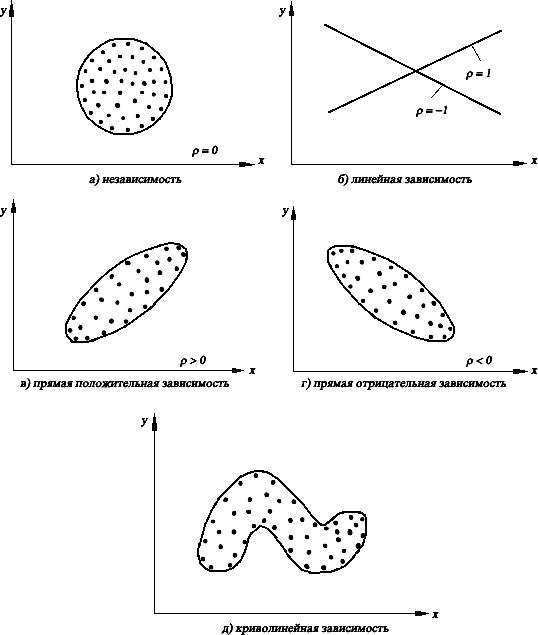



Рис. 2.3.3. Графическая интерпретация взаимосвязи между показателями

Корреляционную зависимость между признаками можно описывать разными способами. В частности, любая форма связи может быть выра- жена уравнением общего вида Y = f(X), где признак Y – зависимая пере-менная,или функцияот независимой переменной X, называемой аргумен-том. Соответствие между аргументом и функцией может быть задано таблицей, формулой, графиком и т. д.