Методы математической обработки данных педагогического исследования. мат пдф (1). Монография Чебоксары 2019 удк 796799 ббк 75. 1 К72 Рецензенты др экон наук, профессор

• Название: Монография Чебоксары 2019 удк 796799 ббк 75. 1 К72 Рецензенты др экон наук, профессор
• Анкор: Методы математической обработки данных педагогического исследования
• Дата: 23.06.2022
• Размер: 0.59 Mb.
• Имя файла: мат пдф (1).docx
• Тип: Монография; #612510
• страница: 20 из 37

Пример 2.3.1. Определить форму и направление взаимосвязи между резуль- татами в беге на 30 и 100 м у 12 исследуемых с помощью построения графика корреляционного поля, если данные выборок таковы:

^xi<sup>, с 4,6; 4,8; 4,9; 4,7; 4,6; 4,8; 4,7; 4,9; 5,0; 4,7; 4,9; 4,8;

y</sup>i^{, с 12,4; 13,1; 13,5; 13,1; 12,5; 13,3; 13,2; 13,7; 13,7; 13,0; 13,6; 13,2.}

Решение.

1. 
   Построим график данного корреляционного поля, отложив на оси Хв порядке возрастания результаты в беге на 30 м, а на оси Y– результаты в беге на 100 м.
   

2. 
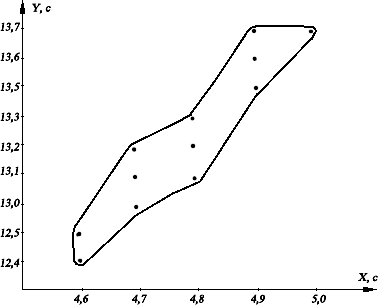
   Делаем вывод о форме и направлении взаимосвязи между исследуемыми показателями.
   

Вывод: график данного корреляционного поля позволяет предположить, что, возможно, между результатами в беге на 30 и 100 м у исследуемой группы наблю- дается прямая, положительная взаимосвязь, т.е. со снижением показателя времени в беге на 30 м будет происходить повышение результатов в беге на 100 м.

Пример 2.3.2. Определить форму и направление взаимосвязи между показате- ^{лями пульса покоя и абсолютными значениями пробы PWC}170 ^{у 15 исследуемых с} помощью построения графика корреляционного поля, если данные выборок таковы: ^xi^{, уд/мин 80; 72; 78; 71; 80; 80; 84; 82; 78; 81; 70; 83;}

72; 73; 81.

^yi^{, кГм/мин 858; 979; 1071; 1071; 920; 1022; 879; 1000; 1004; 1071; 1022; 807;}

1099; 982; 817.

Решение.

1. 
   Построим график данного корреляционного поля, отложив на оси Х в по- рядке возрастания показатели пульса покоя, на оси Y – абсолютные значения ^{пробы PWC}170^.
   

2. 
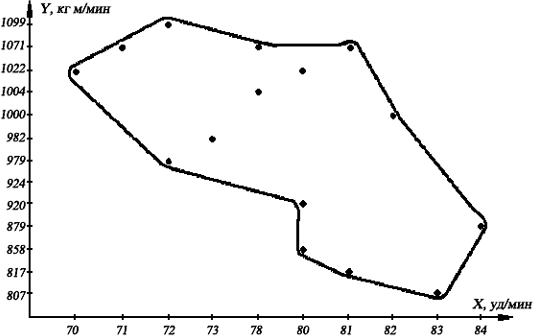
   Делаем вывод о форме и направлении взаимосвязи между исследуемыми показателями.
   

Вывод: график данного корреляционного поля позволяет предположить, что, ^{возможно, между пульса покоя и абсолютными значениями пробы PWC}170 ^{у ис-} следуемой группы наблюдается прямая, обратная зависимость, т.е. со снижением ^{показателя пульса покоя происходит увеличение абсолютных значений PWC}170^.

Коэффициентыкорреляциииихсвойства.

Коэффициент корреляции  для генеральной совокупности, как пра- вило, неизвестен, поэтому он оценивается по экспериментальным дан- ным, представляющим собой выборку объема п пар значений (x_i, y_i), по- лученную при совместном измерении двух признаков Хи Y. Коэффициент корреляции, определяемый по выборочным данным, называется выбороч-нымкоэффициентомкорреляции(или просто эмпирическимкоэффициен-томкорреляции). Его принято обозначать символом r.

Коэффициенты корреляции – удобный показатель связи, получивший широкое применение в практике. К их основным свойствам необходимо отнести следующие:

1. 
   Коэффициенты корреляции способны характеризовать только ли- нейные связи, т.е. такие, которые выражаются уравнением линейной функции. При наличии нелинейной зависимости между варьирующими признаками следует использовать другие показатели связи.
   
2. 
   Значения коэффициентов корреляции – это отвлеченные числа, ле- жащее в пределах от –1 до +1, т.е. –1 < r< 1.
   
3. 
   При независимом варьировании признаков, когда связь между ними отсутствует, r= 0.
   
4. 
   При положительной, или прямой, связи, когда с увеличением значе- ний одного признака возрастают значения другого, коэффициент корре- ляции приобретает положительный (+) знак и находится в пределах от 0 до +1, т.е. 0 <r < 1.
   
5. 
   При отрицательной, или обратной, связи, когда с увеличением зна- чений одного признака соответственно уменьшаются значения другого, коэффициент корреляции сопровождается отрицательным (–) знаком и находится в пределах от 0 до –1, т.е. –1 < r < 0.
   
6. 
   Чем сильнее связь между признаками, тем ближе величина коэффи- циента корреляции к 1. Если r =  1, то корреляционная связь перехо- дит в функциональную, т.е. каждому значению признака Хбудет соответ- ствовать одно или несколько строго определенных значений признака Y.
   
7. 
   Только по величине коэффициентов корреляции нельзя судить о до- стоверности корреляционной связи между признаками. Этот параметр за- висит от числа степеней свободы k = n –2, где: n – число коррелируемых пар показателей Х и Y. Чем больше n, тем выше достоверность связи при одном и том же значении коэффициента корреляции.
   

В практической деятельности, когда число коррелируемых пар при- знаков Хи Yне велико (n 30), то при оценке зависимости между показа- телями используется следующую градацию:

1. 
   высокаястепеньвзаимосвязи– значения коэффициента корреляции находится в пределах от 0,7 до 0,99;
   
2. 
   средняястепеньвзаимосвязи– значения коэффициента корреляции находится в пределах от 0,5 до 0,69;
   
3. 
   слабаястепеньвзаимосвязи– значения коэффициента корреляции находится от 0,2 до 0,49.
   

НормированныйкоэффициенткорреляцииБравэ-Пирсона.

В качестве оценки генерального коэффициента корреляции  исполь- зуется коэффициент корреляции r Бравэ–Пирсона. Для его определения принимается предположение о двумерном нормальном распределении ге- неральной совокупности, из которой получены экспериментальные дан- ные. Это предположение может быть проверено с помощью соответству- ющих критериев значимости. Следует отметить, что если по отдельности одномерные эмпирические распределения значений x_iи y_iсогласуются с нормальным распределением, то из этого еще не следует, что двумерное распределение будет нормальным. Для такого заключения необходимо еще проверить предположение о линейности связи между случайными ве- личинами Х и Y. Строго говоря, для вычисления коэффициента корреля- ции достаточно только принять предположение о линейности связи между случайными величинами, и вычисленный коэффициент корреля- ции будет мерой этой линейной связи.


xy
Коэффициент корреляции Бравэ–Пирсона (r^P ) относится кпарамет-

рическим коэффициентам и для практических расчетов вычисляется по формуле:

_{rP =}∑(x_i–x̄)⋅(y_i–ȳ) _{. (2.3.1)}

^xy √∑(x_i–x̄)²⋅∑(y_i–ȳ )²


xy

xy
Из формулы (2.3.1) видно, что для вычисления r^P необходимо найти средние значения признаков Хи Y, а также отклонения каждого статисти- ческого данного от его среднего (x_i — x̄) ⋅ (y_i — ȳ). Зная эти значения, находятся суммы ^∑(x_i — x̄) ⋅ (y_i — ȳ), ^∑(x_i — x̄)², ^∑(y_i — ȳ)². Затем, вы- числив значение r^P , необходимо определить достоверность найденного коэффициента корреляции, сравнив его фактическое значение с таблич- ным для k = n –2 (прилож. 7). Если r_ф ≥ r_st, то можно говорить о том, что между признаками наблюдается достоверная взаимосвязь. Если r_ф < r_st, то между признаками наблюдается недостоверная корреляционная взаи- мосвязь.

Пример 2.3.3. Определить достоверность взаимосвязи между результатами в беге на 500 м и показателями пульса после выполненной нагрузки у 12 исследуе- мых с помощью расчета нормированного коэффициента корреляции, если данные выборок таковы:

^xi<sup>, с 78,2; 77,8; 78,9; 81,2; 76,5; 79,1; 77,4; 78,9; 79,8; 80,8; 76,4; 77,6;

y</sup>i^{, уд/мин 162; 156; 162; 168; 156; 162; 156; 162; 168; 174; 156; 162.}

Решение.

1. 
   Данные тестирования заносим в рабочую таблицу и сделаем необходимые расчеты.
   

xi	(xi — x̄)	(xi — x̄)2	yi	(yi — ȳ)	(yi — ȳ)2	(xi — x̄)⋅ (yi — ȳ)
78,2	-0,4	0,16	162	0	0	0
77,8	-0,8	0,64	156	-6	36	4,8
78,9	0,3	0,09	162	0	0	0
81,2	2,6	6,76	168	6	36	15,6
76,5	-2,1	4,41	156	-6	36	12,6
79,1	0,5	0,25	162	0	0	0

Окончаниетаблицы

xi	(xi — x̄)	(xi — x̄)2	yi	(yi — ȳ)	(yi — ȳ)2	(xi — x̄)⋅ (yi — ȳ)
77,4 78,9 79,8 80,8 76,4 77,6	-1,2 0,3 1,2 2,2 -2,2 -1,0	1,44 0,09 1,44 4,84 4,84 1,00	156 162 168 174 156 162	-6 0 6 12 -6 0	36 0 36 144 36 0	7,2 0 7,2 26,4 13,2 0
x̄ = 78,6		∑(xi — x̄)2 = 25,96	ȳ =162		∑(yi — ȳ)2 = 360	∑(xi — x̄) ⋅ (yi– ȳ) = 87

2. 
   Рассчитаем значение нормированного коэффициента корреляции Пирсона, используя формулу (10.1):
   

_{rP =}^∑(x_i—x̄)⋅(y_i—ȳ) ₌ 87


_≈ 87
≈ 0,90.

^xy √^∑(x — x̄)² ⋅ ^∑(y — ȳ)² √25,96 ⋅ 360

96,67

i i

3. 
   Рассчитаем число степеней свободы по формуле:
   

k= n–2 = 12 – 2 = 10.

4. 
   Произведем сравнение расчетного значения нормированного коэффициента ^{корреляции (r}ф^{= 0,90) с табличным значением для k= 10 при}  ^{= 1% (прилож. 7) и} сделаем вывод.
   

^{Вывод: 1) т.к. r}ф ^{= 0,90  0, то между данными выборок наблюдается прямая} положительная взаимосвязь, т.е. низкому результату в беге соответствует высо- кий показатель пульса нагрузки;

^{2) т.к. r}ф^{= 0,90  r}st^{= 0,71 для k= 10 при  = 1%, то с уверенностью  = 99% можно} говорить о том, что выявленная зависимость достоверна.