Методы математической обработки данных педагогического исследования. мат пдф (1). Монография Чебоксары 2019 удк 796799 ббк 75. 1 К72 Рецензенты др экон наук, профессор

• Название: Монография Чебоксары 2019 удк 796799 ббк 75. 1 К72 Рецензенты др экон наук, профессор
• Анкор: Методы математической обработки данных педагогического исследования
• Дата: 23.06.2022
• Размер: 0.59 Mb.
• Имя файла: мат пдф (1).docx
• Тип: Монография; #612510
• страница: 23 из 37

Регрессионный анализ

Понятиерегрессии.

В практических исследованиях возникает необходимость аппроксими-ровать (описать приблизительно) диаграмму рассеяния математиче-ским уравнением. То есть зависимость между переменными величинами Yи Хможно выразить аналитически с помощью формул и уравнений и графически в виде геометрического места точек в системе прямоугольных координат. График корреляционной зависимости строится по уравнениям функции ȳ_x = f(x) и x̄_y = f(y), которые называются регрессией (термин “регрессия” происходит от лат. regressio– движение назад).Здесь ȳ_x и x̄_y – средние арифметические из числовых значений зависимых перемен- ных Yи X.

Для выражения регрессии служат эмпирические и теоретические ряды, их графики – линии регрессии, а также корреляционные уравнения(уравнениярегрессии)икоэффициентлинейнойрегрессии.

Показатели регрессии выражают корреляционную связь двусторонне, учитывая изменение средней величины ȳ_x признака Y при изменении зна- чений x_iпризнака X, и, наоборот, показывают изменение средней величины x̄_y признака Хпо измененным значениям y_iпризнака Y.Исключение состав- ляют временные ряды, или ряды динамики, показывающие изменение при- знаков во времени. Регрессия таких рядов является односторонней.

Рядырегрессии, особенно их графики, даютнаглядноепредставлениео форме и тесноте корреляционной связи между признаками, в чем и за- ключается их ценность. Форма связи между показателями, влияющими на уровень спортивного результата и общей физической подготовки занима- ющихся физической культурой и спортом, может быть разнообразной. И поэтому задача состоит в том, чтобы любую форму корреляционной связи выразить уравнением определенной функции (линейной, параболической и т.д.), что позволяет получать нужную информацию о корреляции между переменными величинами Y и X, предвидеть возможные изменения при- знака Yна основе известных изменений X, связанного с Yкорреляционно.

Уравнениелинейнойрегрессии.

Обычно признак Yрассматривается как функция многих аргументов – x₁,x₂,x₃,…,x_m– и может быть записана в виде: y=a+bx₁+cx₂+dx₃+…, где а,b,си d– параметры уравнения, определяющие соотношение между аргументами и функцией. В практике учитываются не все, а лишь некото- рые аргументы, в простейшем случае, как при описании линейной регрес- сии, – всего один:

y =a+bx (2.4.1)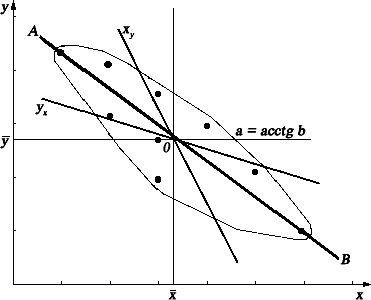

В этом уравнении параметр а – свободный член; графически он пред- ставляет отрезок ординаты (у) в системе прямоугольных координат. Па- раметр bназывается коэффициентомрегрессии. С точки зрения аналити- ческой геометрии b– угловой коэффициент, определяющий наклон линии регрессии по отношению к осям, координат. В области регрессионного анализа этот параметр показывает, насколько в среднем величина одного признака (Y) изменяется при изменении на единицу меры другого корре- ляционно связанного с Y признака X. Наглядное представление об этом параметре и о положении линий регрессии Y по Х и X по Y в системе пря- моугольных координат дает рисунок 2.4.1.

Рис. 2.4.1. Схема линий регрессии Yпо Хи Хпо Yв системе прямоугольных координат

Линии регрессии, как показано, пересекаются в точке 0 (x̄, ȳ), соответ- ствующей средним арифметическим значениям корреляционно связанных друг с другом признаков Yи X. Линия АВ, проходящая через эту точку, изоб- ражает полную (функциональную) зависимость между переменными вели- чинами Yи X, когда коэффициент корреляции r= 1. Чем сильнее связь между Yи X, тем ближе линии регрессии к АВ, и, наоборот, чем слабее связь между варьирующими признаками, тем более удаленными оказываются линии ре- грессии от АВ. При отсутствии связи между признаками, когда r= 0, линии регрессии оказываются под прямым углом (90°) по отношению друг к другу.

Уравнение регрессии тем лучше описывает зависимость, чем меньше рассеяние диаграммы, чем больше теснота взаимосвязи. Уравнение пря- мой линии пригодно для описания только линейных зависимостей. В слу- чае нелинейных зависимостей математическая запись может отобра- жаться уравнениями параболы, гиперболы и др.

Необходимо также сделать одно важное замечание о значении показа- телей, характеризующих взаимосвязь признаков (коэффициентов корре- ляции, регрессии и т. п.). Все они дают лишь количественную меру связи, но ничего не говорят о причинах зависимости. Определить эти причины – дело самого исследователя.

Коэффициентыуравненияпарнойлинейнойрегрессии.

Как уже было определено выше, в случае линейной зависимости урав- нение регрессии является уравнением прямой линии. Таких уравнений два:

Y = a₁ + b_y/x ⋅ X^¯ – прямое

и X = a₂ + b_x/y ⋅ Y^¯ – обратное, (2.4.2)

где aи b– коэффициенты, или параметры, которые надлежит определить.

Значение коэффициентов регрессии вычисляется по формуле:

_{b = r ⋅} σ_{y =} ^∑(x_i—x̄)⋅(y_i—ȳ)

y/x _σx

и

^∑(x_i — x̄)²

_bx/y _{= r ⋅} σ_{x =} ∑(x_i–x̄)⋅(y_i–ȳ )_{. (2.4.3)}

σ_y ∑(y_i–ȳ )²

Коэффициенты регрессии b имеют размерность, равную отношению размерностей изучаемых показателей X и Y, и тот же знак, что и коэффи- циент корреляции.

Коэффициенты аопределяются по формуле:

a₁ = Y^¯ — b_y/x ⋅ X^¯ и a₂ = X^¯ — b_x/y ⋅ Y^¯ . (2.4.4)

Чтобы вычислить этот коэффициенты, надо просто в уравнения ре- грессии подставить средние значения коррелируемых переменных.

Для оценки качества уравнений регрессии вычисляются остаточныесредниеквадратическиеотклонения(или абсолютныепогрешностиуравнений) по формуле:

σ_y/x = σ_y ⋅ ^√1 — r²;



σ_x/y = σ_x ⋅ √1 — r². (2.4.5)

Эти оценки абсолютны и, следовательно, не могут быть сравнимы друг с другом. Поэтому вводят оценки относительнойпогрешностиурав-нений, которые выражаются в процентах и служат для точности пред-сказания (прогнозирования) результатов одного показателя по заранееизвестным значениям другого. Относительные погрешности уравнений регрессии определяются по формуле:

σ^/ = ^σy/x ⋅ 100%;

y/x _ȳ

σ^/ = ^σx/y ⋅ 100%. (2.4.6)

x/y _x̄

Значение этой оценки, если r = 1, равно нулю и, если r = 0, макси- мально. Остаточное среднее квадратическое отклонение характеризует колеблемость Y относительно линии регрессии по Х в прямом уравнении регрессии и, наоборот, в обратном случае. А, следовательно, чем меньше величина относительной погрешности уравнения регрессии, тем точнее будет оно осуществлять прогноз значений одного показателя по заранее известным значениям другого.

Связьмеждукоэффициентамирегрессииикорреляции.

Между коэффициентом корреляции и параметром парной линейной регрессии существует зависимость, которая применительно к выбороч- ным оценкам может быть представлена следующим образом:

b = r ⋅ ^σY¯ , (2.4.7)

σ_X¯

^{где σY}¯ ^{и σX}¯ ^{– средние квадратические ошибки.}

Приведенное выражение позволяет оценить параметр регрессии без решения системы нормальных уравнений при условии, что коэффициент корреляции уже определен. На основе формулы (2.4.7) легко показать, что выборочный коэффициент корреляции равен среднему геометрическому выборочных коэффициентов регрессии. Действительно, сравнив фор- мулы (2.4.3) с основной формулой (2.3.1) коэффициента корреляции, ви- дим, что их числители равны ^∑(x_i — x̄) ⋅ (y_i — ȳ). Это свидетельствует об определенной связи между этими характеристиками. Выборочный коэф- фициент корреляции выражается тогда равенством r²=b_y/x b_x/y, откуда

r = ±_√b_y/x ⋅ b_x/y. (2.4.8)

Эта формула ценна тем, что, во-первых, может быть использована для нахождения неизвестной величины коэффициента корреляции по извест- ным значениям коэффициента регрессии b_y/xи b_x/y,а во-вторых, позволяет контролировать правильность расчета коэффициента корреляции, если известны величины b_y/xи b_x/y. Знак выборочного коэффициента корреля- ции совпадает со знаком выборочных коэффициентов регрессии, что сле- дует из формулы (2.4.3). Если зависимость между признаками функцио-

b
нальная, то b_y/x = ¹

x/y

и, следовательно, r= 1. И, наоборот, при полном

отсутствии взаимосвязи между признаками b_y/x= 0, b_x/y= 0 и r= 0.

Определениепараметровпарнойлинейнойрегрессии.

Определение параметров линейной регрессии – одна из задач регрес- сионного анализа. Она решается способом наименьших квадратов, осно- ванным на требовании, чтобы сумма квадратов отклонений вариант от ли- нии регрессии была наименьшей. Этому требованию удовлетворяет сле- дующая система нормальных уравнений:
Ряды регрессии – это ряды усредненных значений (y_xи x_y) варьирую- щих признаков Yи X,соответствующих значениям аргументов y_iи x_i.По- этому эмпирические уравнения регрессии следует записывать так:

y_x=a_y/x+b_y/x xи x_y=a_x/y+b_x/y y. (2.4.9)

Формулы для определения параметров а и b принимают следующие выражения:

a_y/x = ȳ — b_y/x ⋅ x̄;

a_x/y = x̄ — b_x/y ⋅ ȳ. (2.4.10)

Уравнение линейной регрессии можно выразить в виде отклонений ва- риант от их средних арифметических:

y_x — ȳ = b_y/x ⋅ (x_i — x̄);

x_y — x̄ = b_x/y ⋅ (y_i — ȳ). (2.4.11)

В таком случае система нормальных уравнений для определения пара- метров аи bбудет следующая:

an + b Σ(x_i — x̄) = Σ(y_i — ȳ);
a Σ(x_i — x̄) + b Σ(x_i — x̄)² = Σ(x_i — x̄) ⋅ (y_i — ȳ).

Поскольку ^∑(x_i — x̄) = 0 и ^∑(y_i — ȳ) = 0, то параметр b выразится в виде приведенной формулы (2.2.3); параметр алегко найти по формуле (2.4.4).

Если средние ȳ и x̄ перенести в правую часть уравнения (2.4.11), то при a = ȳ система нормальных уравнений принимает следующий вид:

y_x = ȳ + b_y/x ⋅ (x_i — x̄);

x_y = x̄ + b_x/y ⋅ (y_i — ȳ). (2.4.12)

Заменив в формуле (2.4.12) параметры b_y/xи b_x/yна их значения из фор- мулы (2.4.3), получим систему уравнений парной линейной регрессии:

_{y = ȳ +} ^∑(x_i—x̄)⋅(y_i—ȳ) _{⋅ (x — x̄);}

^{x ∑}(x_i — x̄)²


y
x = x̄ + ^{∑(xi–x̄)⋅(yi–ȳ)} ⋅ (y — ȳ). (2.4.13)

∑(y_i–ȳ )²

Эти уравнения удобны для определения параметров при отыскивании эмпирических уравнений регрессии в практической работе для точности прогнозирования результатов.

Графическоепредставлениеуравненияпарнойлинейнойрегрессии.

Эмпирические ряды регрессии Y по Х и Х по Y изображаются в виде линейного графика, при построении которого наиболее точным является использование способа наименьших квадратов, предложенного в 1806 г. К. Гауссом и независимо от него А. Лежандром. В основу этого способа положена теорема, согласно которой сумма квадратов отклонений вари- ант (x_i) от среднего арифметического (x̄) есть величина наименьшая, т. е.

^∑ (x_i — x̄)² = min. Отсюда и название метода, который нашел широкое применение не только в биологии, но и в технике. Мы уже говорили об этом методе и применяли его, когда находили параметры а и b линейной регрессии, отыскивая эмпирическое уравнение.

При графическом изображении эмпирического уравнения регрессии (например, показатели роста и веса 10 исследуемых спортсменов), пред- ставленного на рисунке 2.4.2 используется следующая последовательность:

1. 
   Определив форму и направление взаимосвязи между эмпириче- скими данными на основе данных расчета нормированного коэффициента корреляции, производят расчет уравнений регрессии (прямого и обрат- ного) по формуле (2.4.13).
   
2. 
   Подставляя в конечный вид уравнений, выражающих зависимость между переменными величинами Yи X,эмпирические данные x_iи y_iнахо- дят координаты точек линий регрессии для усредненных значений y_xи x_y.
   
3. 
   На графике, выполненном в прямоугольной системе координат, на оси хоткладывают значения переменных x_i, на оси у– значения y_iи отме- чают точками рассчитанные координаты линий регрессии для усреднен- ных значений y_xи x_y(рис. 2.4.2).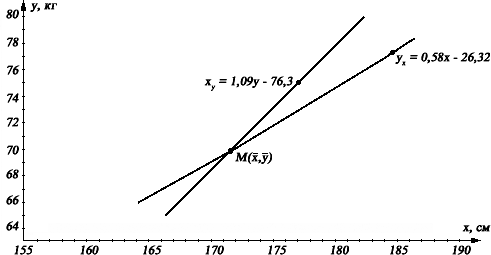
   
4. 
   Две линии регрессии на графике пересекаются в точке М с коорди- натами средних значений показателей x_iи y_i.
   

Рис. 2.4.2. Графическое изображение эмпирического уравнения регрессии

График линий регрессии отражает ряды теоретически ожидаемых зна- чений функции по известным значениям аргумента. При этом, чем силь- нее взаимосвязь между величинами x_iи y_i, тем меньше угол между лини- ями регрессии. При r = 1 линии уравнения регрессии либо совпадают, либо расположены параллельно, так как корреляционная зависимость между признаками в этом случае переходит в функциональную. И, наобо- рот, чем слабее зависимость между признаками, тем больше угол между линиями на графике. При r = 0 линии регрессии расположены перпенди- кулярно.

Пример 2.4.1. Рассчитать и построить график уравнения прямолинейной ре- грессии для показателей роста и веса 8 исследуемых и сделать вывод о точности расчета уравнений, если данные выборок таковы:

^xi<sup>, см 166; 180; 173; 174; 185; 179; 168; 171;

y</sup>i^{, кг 63; 75; 70; 70; 73; 75; 65; 70.}