Методы математической обработки данных педагогического исследования. мат пдф (1). Монография Чебоксары 2019 удк 796799 ббк 75. 1 К72 Рецензенты др экон наук, профессор

• Название: Монография Чебоксары 2019 удк 796799 ббк 75. 1 К72 Рецензенты др экон наук, профессор
• Анкор: Методы математической обработки данных педагогического исследования
• Дата: 23.06.2022
• Размер: 0.59 Mb.
• Имя файла: мат пдф (1).docx
• Тип: Монография; #612510
• страница: 21 из 37

Пример 2.3.4. Определить достоверность взаимосвязи между показателями веса и количеством подтягиваний на перекладине у 11 исследуемых с помощью расчета нормированного коэффициента корреляции, если данные выборок та- ковы:

^xi^{, кг} 51; 50; <sup>48; 51; 46; 47; 49; 60; 51; 52; 56;

y</sup>i^{, кол-раз 13; 15; 13; 16; 12; 14; 12; 10; 18; 10; 12.}

Решение.

1. 
   Данные тестирования заносим в рабочую таблицу и сделаем необходимые расчеты.
   

xi	(xi — x̄)	(xi — x̄)2	yi	(yi — ȳ)	(yi — ȳ)2	(xi — x̄)⋅ (yi — ȳ)
51 50 48 51 46 47 49 60 51 52 56	0 -1 -3 0 -5 -4 -2 9 0 1 5	0 1 9 0 25 16 4 81 0 1 25	13 15 13 16 12 14 12 10 18 10 12	0 2 0 3 -1 1 -1 -3 5 -3 -1	0 4 0 9 1 1 1 9 25 9 1	0 -2 0 0 5 -4 2 -27 0 -3 -5
x̄ = 51		∑(xi — x̄)2 = 162	ȳ =13		∑(yi — ȳ)2 = 60	∑(xi — x̄)⋅ (yi — ȳ) = -34

2. 
   Рассчитаем значение нормированного коэффициента корреляции Пирсона, используя формулу (2.3.1):
   

_{rP =} ^∑(x_i—x̄)⋅(y_i—ȳ) ₌ —34


_≈ —34
≈ —0,34.

^xy √^∑(x — x̄)² ⋅ ^∑(y — ȳ)^{2 √162 ⋅ 60}

98,59

i i

3. 
   Рассчитаем число степеней свободы по формуле:
   

k= n–2 = 11 – 2 = 9.

4. 
   Произведем сравнение расчетного значения нормированного коэффициента ^{корреляции (r}ф ^{= -0,34) с табличным значением для k = 9 при}  ^{= 5% (прилож. 7)} и сделаем вывод.
   

^{Вывод: 1) т.к. r}ф ^{= -0,34  0, то между данными выборок наблюдается прямая} отрицательная взаимосвязь, т.е. с увеличение показателей веса у исследуемых снижается их результат в количестве подтягиваний на перекладине;

^{2) т.к. r}ф^{= -0,34  r}st^{= 0,60 для K= 10 при  = 5%, то с уверенностью  = 95%}

можно говорить о том, что выявленная зависимость недостоверна.
Оценка достоверности коэффициента корреляции.Ошибкаэмпирическогокоэффициентакорреляции.

Эмпирический коэффициент корреляции служит оценкой генераль- ного параметра  и как случайная величина сопровождается ошибкой, ко- торая определяется по формуле

r
_{s =} 1–r²

√ⁿ

(2.3.2)

или, когда объем выборки не превышает 100 наблюдений,


s = ^√1–r2 = ^√1–r2. (2.3.3)

^r √^n–2

n–2

Отношение выборочного коэффициента корреляции к своей ошибке служит критерием для проверки нулевой гипотезы – предложения о том, что в генеральной совокупности этот показатель равен нулю, т. е.  = 0.

Нулевая гипотеза опровергается, если

t_ф = ^r⋅√n ≥ t_st или t_ф = ^r⋅√n–2 = r ⋅ √ ^n–2 ≥ t_st (при n 100)

1–r<sup>2

√</sup>1–r²

1–r²

для k=n–2и принятого уровня значимости ().

^{Пример_2.3.5.'>Пример 2.3.5. Для найденной величины коэффициента корреляции r}ху ^{= 0,90 между} результатами в беге на 500 м и показателями пульса после нагрузки у 12 исследу- емых (пример 2.3.3) t-критерий определяется следующим образом:

ф ₂
t = 0,90 ⋅ √ ^{12 — 2}

1 — (0,90)
≈ 6,53.

^{Вывод:т.к. t}ф^{= 6,53 > t}st^{= 4,59 для 0,1%-ного уровня значимости и k= 10 (при-} лож. 1), нулевая гипотеза о том, что в генеральной совокупности значение  = 0, опровергается.

Пример 2.3.6. Проверим нулевую гипотезу ( = 0) в отношении коэффициента корреляции, равного –0,34, между показателями веса и количеством подтягиваний на перекладине у 11 исследуемых (пример 2.3.4). В данном случае

ф ₂
t = ^|—0,34^| ⋅ √ ^{11 — 2}

1 — (—0,34)
≈ 1,08.

^{Вывод:т.к. t}ф ^{= 1,08 < t}st^{= 2,26 для k= 11 – 2 = 9 и 5%-ного уровня значимости}

(прилож. 1), то нулевая гипотеза о том, что в генеральной совокупности значение

 = 0 подтверждается (р< 0,05).

Значимость, или достоверность, коэффициента корреляции можно установить, пользуясь также таблицей приложения 7. Нулевая гипотеза опровергается, если эмпирический коэффициент корреляции превысит указанную в таблице величину для принятого уровня значимости и числа степеней свободы k=n – 2. Так, для k = 10 и  = 1 % в таблице приложе- ния 7 находим 0,79. Поскольку найденный в примере 2.3.3 эмпирический коэффициент корреляции r_xy= 0,90 выше стандарта, нулевая гипотеза о том, что в генеральной совокупности  = 0, отрицается. Если же значение эмпирического коэффициента корреляции ниже стандарта (пример 2.3.4), то нулевая гипотеза подтверждается на 5%-ном уровне значимости.

Установлено, что при малом объеме выборки эмпирический коэффи- циент корреляции (r) оказывается несколько ниже, чем генеральный па- раметр (). Поэтому лучшая оценка  получается по формуле (Л. Закс, 1976):

r^∗ = r ⋅ [1 +

1 — r²

].

2(n — 3)

Так, в отношении корреляции между результатами в беге на 500 м и показателями пульса после нагрузки у 12 исследуемых более точной оценкой генерального параметра (_ху) будет величина

xy
r^∗ = 0,90 ⋅ [1 +

1 — (0,90)²

_{2(12 — 3)} ] = 0,9095 ≈ 0,91.

Разумеется, что при наличии большого числа наблюдений (n > 100) эта поправка оказывается незначительной и ее можно не вносить.

Правильное применение коэффициента корреляции предполагает нор- мальность распределения двумерной совокупности сопряженных значе- ний случайных переменных величин Yи X.Из математической статистики известно, что при малом числе испытаний и сравнительно сильной корре- ляции (r> 0,5) распределение коэффициента корреляции п-го числа выбо- рок, взятых из нормально распределяющейся совокупности, значительно отклоняется от нормальной кривой. Это показано на рисунке 2.3.4, где изображены кривые распределения эмпирического коэффициента корре- ляции при n = 12 для значений генерального параметра  = 0; 0,4 и 0,8. При значениях , приближающихся к единице, кривая распределения эм- пирического коэффициента корреляции (r) становится все более асиммет- ричной. Следовательно, эмпирический коэффициент корреляции не будет точной оценкой генерального параметра (), если он вычислен на мало- численной выборке и его величина значительно отклоняется от 0,5.

26. 
    преобразованиеФишера
    

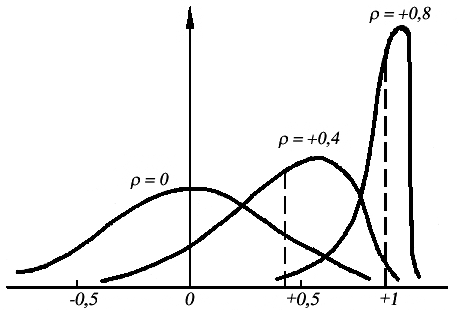
Рис. 2.3.4. Кривые распределения эмпирического коэффициента корреляции (r) при n = 12 для разных значений генерального параметра 

Имея в виду это обстоятельство, Фишер нашел более точный способ оценки генерального параметра  по величине выборочного коэффици- ента корреляции r. Этот способ сводится к замене коэффициента корре- ляции преобразованной величиной z, которая связана с эмпирическим ко- эффициентом корреляции, следующим образом:

z = ¹ ln⋅ ^1+r, или z = 1,15129 lg⋅ ^1+r.

2 1–r 1–r

Распределение величины z является почти неизменным по форме, так как мало зависит от численности выборки и от значения коэффициента корреляции в генеральной совокупности. Величина z меняет свое значе- ние от – до +,а ее распределение быстро приближается к нормальному распределению со средним значением (рис. 2.3.5)

z̄ = ¹ ln⋅ ^1+ρ + ^ρ и дисперсией σ² = ¹ .

2 1–ρ

2(n–1)

^Z n–3

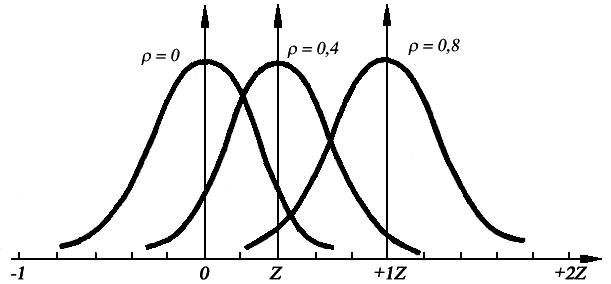
Рис. 2.3.5. Распределение величины z при n = 12

Преобразование коэффициента корреляции в величину zпроизводится по таблице приложения 8. В таблице содержатся величины z, соответству- ющие значениям эмпирического коэффициента корреляции r. Критерием достоверности показателя zслужит следующее отношение:

t = ^z = z ⋅ √n — 3.

z _sz

Этот критерий пригоден для выборки любого объема; он используется во всех случаях, когда вместо коэффициента корреляции r берется отве- чающее ему значение z. Нулевая гипотеза проверяется с помощью t-кри- терия Стьюдента для принятого уровня значимости и числа степеней сво- боды k=n–2.

Применение z-преобразования позволяет с большей уверенностью оценивать значимость эмпирического коэффициента корреляции, а также и разность между двумя выборочными коэффициентами r₁–r₂, когда воз- никает такого рода необходимость.

Проверим нулевую гипотезу в отношении преобразованного по z ко- эффициента корреляции между результатами в беге на 500 м и показате- лями пульса после нагрузки у исследуемых. Этот показатель, полученный в результате 12 наблюдений, оказался равным r = 0,90. В приложении 8 этой величине соответствует z = 1,472. Критерий t_ф= 1,472  √12 — 3= 1,472  3 = 4,416. Для k = 12 – 2 = 10 и 1%-ного уровня значимости в приложении 1 находим t_st= 3,17. Так как t_ф>t_st, нулевая гипотеза должна быть отвергнута.

Минимальное число наблюдений для планируемой точности коэффи-циента корреляции.

Статистическая недостоверность вычисленного на малочисленной вы- борке коэффициента корреляции ничего, собственно, не доказывает. Ведь при повторной выборке нулевая гипотеза может оказаться несостоятель- ной. Можно рассчитать необходимый объем выборки для заданной точ- ности коэффициента корреляции. Для этого служит формула


n = ₂ + 3,
_t2

(2.3.4)

z

где п – искомый объем выборки, t – величина, заданная по принятому уровню значимости; z – преобразованная (по Фишеру) величина эмпири- ческого коэффициента корреляции.

Пример 2.3.7. Эмпирический коэффициент корреляции, рассчитанный для n= 14, ^{оказался равным 0,482. Этой величине соответствует z = 0,523. Критерий t}z^=0,523√^{14—3 = 1,73. В приложении 1 для 5%-ного уровня значимости и k =14 – 2=12 находим t}st^{= 2,18. Нулевая гипотеза остается в силе. Воспользуемся формулой} (2.3.5) и определим необходимое число наблюдений, чтобы с  = 1%, которому соответствует t= 2,58, можно было бы судить о достоверности этого выборочного коэффициента:

(2,58)²

n = ₂ + 3 ≈

6,656

+ 3 = 24 + 3 = 27.

(0,523) 0,274

Вывод: число наблюдений (п) нужно довести, по меньшей мере, до 27, чтобы удовлетворить требованию выдвинутых условий, т. е. с вероятностью р> 0,99 от- вергнуть нулевую гипотезу и считать выборочный коэффициент корреляции ста- тистически достоверным.

Оценкаразностимеждукоэффициентамикорреляции.

При сравнении коэффициентов корреляции, вычисленных на незави- симых выборках, нулевая гипотеза сводится к предположению, что в ге- неральной совокупности разница между этими показателями равна нулю. Нулевая гипотеза проверяется с помощью t-критерия, который представ- ляет отношение разности между эмпирическими коэффициентами корре- ляции r₁и r₂к ее статистической ошибке, определяемой по формуле

^{sdz =} √^{s2 + s2 , (2.3.5)}

r₁ r₂

где s² и s² – ошибки сравниваемых коэффициентов корреляции, вычис-

r₁ r₂

ляемые по формулам (2.3.2) и (2.3.3), смотря по объемам выборок, для ко- торых вычислены коэффициенты корреляции.

Нулевая гипотеза отбрасывается при t_ф>t_stдля принятого уровня зна- чимости () и числа степеней свободы k = (n₁ – 2) + (n₂ – 2) = n₁ + n₂ – 4. Более точная оценка разности между коэффициентами корреляции, вычисленными на малочисленных выборках, получается при использова- нии метода z, т. е. на основании преобразованных коэффициентов корре- ляции. При этом t-критерий определяется по разности z₁ – z₂, отнесенной

к своей ошибке:

t_dz =^z1–z2. (2.3.6)

_√1 ₊1

n₁—3 n₂—3