Методы математической обработки данных педагогического исследования. мат пдф (1). Монография Чебоксары 2019 удк 796799 ббк 75. 1 К72 Рецензенты др экон наук, профессор

• Название: Монография Чебоксары 2019 удк 796799 ббк 75. 1 К72 Рецензенты др экон наук, профессор
• Анкор: Методы математической обработки данных педагогического исследования
• Дата: 23.06.2022
• Размер: 0.59 Mb.
• Имя файла: мат пдф (1).docx
• Тип: Монография; #612510
• страница: 24 из 37

Решение.

1. 
   Данные тестирования заносим в рабочую таблицу и сделаем соот- ветствующие расчеты.
   

xi	(xi — x̄)	(xi — x̄)2	yi	(yi — ȳ)	(yi — ȳ)2	(xi — x̄) ⋅ (yi — ȳ)
166	-9	81	63	-7	49	63
180	5	25	75	5	25	25
173	-2	4	70	0	0	0
174	-1	1	70	0	0	0
185	10	100	73	3	9	30
179	4	16	75	5	25	20
168	-7	49	65	-5	25	35
171	-4	16	70	0	0	0
x̄ = 175		∑(xi — x̄)2 = 292	ȳ = 70		∑(yi — ȳ)2 = 133	∑(xi — x̄)⋅ (yi — ȳ) = 173

2. 
   Рассчитаем значение нормированного коэффициента корреляции по формуле (2.3.1):
   

xy
_{rP =}^∑(x_i — x̄) ⋅ (y_i — ȳ) ₌ 173


_≈ 173

≈ 0,88.

√^∑(x_i — x̄)² ⋅ ^∑(y_i — ȳ)^{2 √292 ⋅ 133}

197,07

3. 
   Произведем расчет конечного вида уравнений парной линейной ре- грессии по формуле (2.4.13):
   

y = ȳ + ^{∑(xi —x̄)⋅(yi—ȳ)} ⋅ ⁽x — x̄⁾ = 70 + ¹⁷³ ⋅ ⁽x — 175⁾ ≈ 70 + 0,59x — 103,25 ≈

^{x ∑}(x_i — x̄)²

≈ 0,59x — 33,25;

292

x = x̄ + ^{∑(xi—x̄)⋅(yi— ȳ)} ⋅ ⁽y — ȳ⁾ = 175 + ¹⁷³ ⋅ ⁽y — 70⁾ ≈ 175 + 1,3y — 91 ≈

^{y ∑}(y_i — ȳ)²

≈ 1,3y + 84.

133

То есть yx = 0,59x – 33,25; xy = 1,3y + 84.

4. 
   Рассчитаем абсолютные погрешности уравнений регрессии по фор- муле (2.4.5):
   

σ = σ ⋅ ^√1— r² = ^√292 ⋅ √1 — 0,7744 ≈ 3,07 кг;

y/x y ₇

σ = σ ⋅ ^√1— r² = ^√133 ⋅ √1 — 0,7744 ≈ 2,07 см.

x/y x ₇

4. 
   Рассчитаем относительные погрешности уравнений регрессии по формуле (2.4.6):
   

σ^/ = ^σy/x ⋅ 100% = ^3,07 ⋅ 100% ≈ 4,39%;



^y/x y 70

σ^/ = ^σx/y ⋅ 100% = ^2,07 ⋅ 100% ≈ 1,18%.

x/y _x

175

6. 
   Для графического представления корреляционной зависимости между при- знаками рассчитаем координаты линий регрессии, подставив в конечный вид уравнений регрессии данные любого исследуемого (например, первого из списка).
   

Тогда: 1. при х= 166 см у = 64,69 кг  64,7 кг; 2. при у= 63 кг х= 165,9 см  166 см.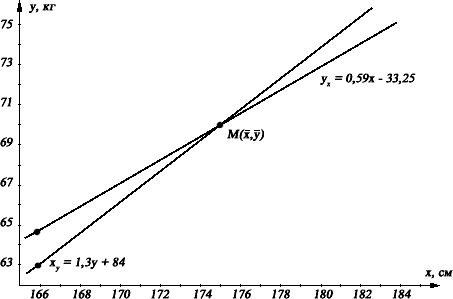

6. 
   Построим график данного уравнения регрессии и сделаем вывод.
   

Вывод:1) с уверенностью в 99% можно утверждать, что в исследуемой группе наблюдается тесная положительная взаимосвязь между показателями роста и веса, т.к. rху = 0,88  rst = 0,83 для k = 6 (прилож. 7);

2. 
   относительная погрешность ху = 1,3у + 84 меньше (1,18%), следовательно, более точно прогнозировать показатель роста исследуемых по данным их веса;
   
3. 
   на графике линии уравнения регрессии располагаются под острым углом, так как значения коэффициента корреляции близки к единице.
   

Пример 2.4.2. Рассчитать и построить график уравнения прямолинейной ре- ^{грессии для относительных значений PWC}170 ^{и времени челночного бега 3х10 м у} 13 исследуемых и сделать вывод о точности расчета уравнений, если данные вы- борок таковы:

^xi^{, кГ м/мин/кг 15,6; 13,4; 17,9; 12,8; 10,7; 15,7; 11,7; 12,3; 12,3; 11,1; 14,3;}

12,7; 14,4;

^yi^{, с 6,9; 7,2; 7,1; 6,7; 7,6; 7,0; 6,4; 6,9; 7,7; 7,6; 7,9; 8,2; 6,8.}

Решение.

1. 
   Данные тестирования заносим в рабочую таблицу и сделаем соответствую- щие расчеты.
   

xi	(xi — x̄)	(xi — x̄)2	yi	(yi — ȳ)	(yi — ȳ)2	(xi — x̄) ⋅ (yi — ȳ)
15,6	2,1	4,41	6,9	-0,3	0,09	-0,63
13,4	-0,1	0,01	7,2	0	0	0
17,9	4,4	19,36	7,1	-0,1	0,01	-0,44
12,8	-0,7	0,49	6,7	-0,5	0,25	0,35
10,7	-2,8	7,84	7,6	0,4	0,16	-1,12
15,7	2,2	4,84	7,0	-0,2	0,04	-0,44
11,7	-1,8	3,24	6,4	-0,8	0,64	1,44
12,3	-1,2	1,44	6,9	-0,3	0,09	0,36
12,3	-1,2	1,44	7,7	0,5	0,25	-0,60
11,1	-2,4	5,76	7,6	0,4	0,16	-0,96
14,3	0,8	0,64	7,9	0,7	0,49	0,56
12,7	-0,8	0,64	8,2	1	1	-0,80
14,4	0,9	0,81	6,8	-0,4	0,16	-0,36
x̄ = 13,5		∑(xi — x̄)2= = 50,92	ȳ = 7,2		∑(yi — ȳ)2= = 3,34	∑(xi — x̄) ⋅ (yi — ȳ)= = -2,64

2. 
   Рассчитаем значение нормированного коэффициента корреляции по фор- муле (2.3.1):
   

_{rP =} ^∑(x_i—x̄)⋅(y_i—ȳ) ₌ —2,64


≈ ^—2,64 ≈ —0,20.

^xy √^∑(x — x̄)² ⋅ ^∑(y — ȳ)² √50,92 ⋅ 3,34

13,04

i i

3. 
   Произведем расчет конечного вида уравнений парной линейной регрессии по формуле (2.4.13):
   

y = ȳ + ^{∑(xi—x̄)⋅(yi—ȳ)} ⋅ ⁽x — x̄⁾ = 7,2 + ^—2,64 ⋅ ⁽x — 13,5⁾

^{x ∑}(x_i — x̄)²

50,92

≈ 7,2 — 0,05x + 0,675 ≈ 7,875 — 0,05x;

x = x̄ + ^{∑(xi—x̄)⋅(yi—ȳ)} ⋅ ⁽y — ȳ⁾ = 13,5 + ^—2,64 ⋅ ⁽y — 7,2⁾ ≈

^{y ∑}(y_i — ȳ)²

3,34

≈ 13,5 — 0,79y + 5,688 ≈ 19,188 — 0,79y.

То есть yx = 7,875 – 0,05x; xy = 19,188 – 0,79y.

4. 
   Рассчитаем абсолютные погрешности уравнений регрессии, используя фор- мулу (2.4.5):
   

σ = σ ⋅ ^√1 — r² = ^√3,34 ⋅ √1 — 0,04 ≈ 0,52 c;

y/x y ₁₂

σ = σ ⋅ ^√1 — r² = ^√50,92 ⋅ √1 — 0,04 ≈ 2,02 кГм/мин/кг.

x/y x ₁₂

5. 
   Рассчитаем относительные погрешности уравнений регрессии по формуле
   

(2.4.6):

σ^/ = ^σy/x ⋅ 100% = ^0,52 ⋅ 100% ≈ 7,22%;

y/x _y

7,2

σ^/ = ^σx/y ⋅ 100% = ^2,02 ⋅ 100% ≈ 14,96%.

x/y _x

13,5

6. 
   Для графического представления корреляционной зависимости между при- знаками рассчитаем координаты линий регрессии, подставив в конечный вид уравнений регрессии данные любого исследуемого (например, четвертого из списка):
   

Тогда: 1) при х= 12,8 кГм/мин/кг у = 7,235 с  7,2 с;

2) при у= 6,7 с х= 13,895 кГм/мин/кг  13,9 кГм/мин/кг.

7. 
   Построим график данного уравнения регрессии и сделаем вывод.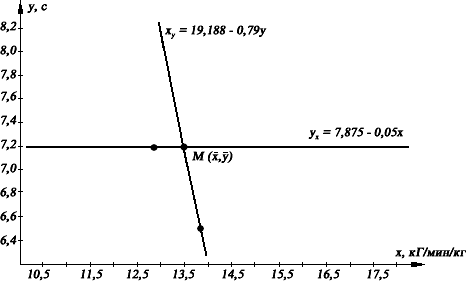
   

Вывод:1) в исследуемой группе наблюдается недостоверная обратная взаимосвязь между данными относительных значений PWC170 и времени челночного бега 3х10 м, т.к. rху = -0,20  rst = 0,55 для k = 11 при = 95% (прилож. 7);

2. 
   относительная погрешность у = 7,875 – 0,05х меньше (7,22%), сле- довательно, более точно прогнозировать результат в челночном беге по данным относительных значений пробы PWC170;
   
3. 
   на графике линии уравнения регрессии расположены почти под пря- мым углом, так как значения коэффициента корреляции близки к нулю.
   

Коэффициентдетерминации.

Квадрат коэффициента корреляции называется коэффициентом де-терминации(D), и в некоторых случаях тесноту взаимосвязи определяют на основании его расчета, который производится по формуле:

D = r² ⋅ 100%. (2.4.14)

Этот коэффициент определяет часть общей вариации одного показа- теля, которая объясняется вариацией другого показателя. Иначе говоря, коэффициент детерминации является мерой определенности линейной

y/x
регрессии. Чем больше коэффициент детерминации, тем меньше наблю- даемые значения y_iпри каждом значении x_iотклоняются от линии регрес- сии Yна X,тем точнее определена линия регрессии. Так, например, если r = 0,90, то D = 81 % общего рассеяния значений y_i(характеризуемого дисперсией σ² ) можно объяснить линейной связью с изменяющимися значениями x_i.

Пример 2.4.3. 10 студентов первого курса, специализирующиеся в легкой ат- летике, были подвергнуты испытаниям в следующих контрольных упражнениях ^{(тестах): беге с ходу на дистанции 30 м (результаты в секундах – x}i^{) и тройном прыжке с места (результаты в метрах – y}i^{). Определить тесноту взаимосвязи между} данными проведенных тестов с помощью расчета коэффициента детерминации.

Решение.

1. 
   Данные тестирования заносим в рабочую таблицу и сделаем необходимые расчеты.
   

xi	(xi — x̄)	(xi — x̄)2	yi	(yi — ȳ)	(yi — ȳ)2	(xi — x̄) ⋅ (yi — ȳ)
3,5	-0,13	0,0169	8,05	0,72	0,5184	-0,094
3,6	-0,03	0,0009	7,34	0,01	0,0001	0,000
3,6	-0,03	0,0009	7,37	0,04	0,0016	-0,001
3,6	-0,03	0,0009	7,77	0,44	0,1936	-0,013
3,8	0,17	0,0289	7,04	-0,29	0,0841	-0,049
3,7	0,07	0,0049	7,17	-0,16	0,0256	-0,011
3,9	0,27	0,0729	6,50	-0,83	0,6889	-0,224
3,4	-0,23	0,0529	8,15	0,82	0,6724	-0,189
3,6	-0,03	0,0009	6,98	-0,35	0,1225	0,010
3,6	-0,03	0,0009	6,97	-0,36	0,1296	0,011
x̄=3,63		∑(xi — x̄)2=0,181	ȳ=7,33		∑(yi — ȳ)2=2,4368	∑(xi — x̄) ⋅ (yi — – ̄y)=-0,560

2. 
   Рассчитаем значение нормированного коэффициента корреляции Пирсона, используя формулу (2.3.1):
   

_{rP =} ^∑(x_i—x̄)⋅(y_i—ȳ) ₌ —0,560


≈ ^—0,560 ≈ —0,84.

^xy √^∑(x — x̄)² ⋅ ^∑(y — ȳ)^{2 √0,181 ⋅ 2,4368}

0,664

i i

3. 
   Рассчитаем для вычисленного значения r= -0,84 значение коэффициента детерминации, используя формулу (2.3.2):
   

D = (—0,84)² ⋅ 100% = 70,56%.

Вывод: следовательно, только 70,56% взаимосвязи спортивного результата в беге на 30 м и в тройном прыжке объясняется их взаимовлиянием. Остальная часть (100% – 70,56% = 29,44%) вариации объясняется влиянием других неучтенных факторов.