Методы математической обработки данных педагогического исследования. мат пдф (1). Монография Чебоксары 2019 удк 796799 ббк 75. 1 К72 Рецензенты др экон наук, профессор

• Название: Монография Чебоксары 2019 удк 796799 ббк 75. 1 К72 Рецензенты др экон наук, профессор
• Анкор: Методы математической обработки данных педагогического исследования
• Дата: 23.06.2022
• Размер: 0.59 Mb.
• Имя файла: мат пдф (1).docx
• Тип: Монография; #612510
• страница: 15 из 37

Пример 2.2.5. С помощью метода Стьюдента определить достоверность раз- личий в показателях роста у 11 учеников первого класса, проведенных в начале и конце учебного года, если данные выборок таковы:

^{Начало года: x}i<sup>, см 136; 130; 127; 132; 125; 138; 120; 131; 118; 123; 128.

Конец года: y</sup>i^{, см 139; 135; 131; 136; 128; 142; 125; 135; 122; 124; 132.}

Решение.

1. 
   Данные тестирования заносим в рабочую таблицу и сделаем необходимые расчеты.
   

Xi	yi	zi= (xi–yi)	(zi — z̄)	(zi — z̄)2
136	139	-3	-3 + 4 = 1	1
130	135	-5	-5 + 4 = -1	1
127	131	-4	-4 + 4 = 0	0
132	136	-4	-4 + 4 = 0	0
125	128	-3	-3 + 4 = 1	1
138	142	-4	-4 + 4 = 0	0
120	125	-5	-5 + 4 = -1	1
131	135	-4	-4 + 4 = 0	0
118	122	-4	-4 + 4 = 0	0
123	124	-1	-1 + 4 = 3	9
128	132	-4	-4 + 4 = 0	0
x̄ =128	ȳ =132	z̄ =-4		∑(zi — z̄)2 =13

2. 
   На основании расчета средних величин выборок выдвигаем рабочую гипотезу. Рабочая гипотеза: т.к. x̄ =128 см  ȳ =132 см, то предположим, что в течение учебного года у исследуемых наблюдается достоверное увеличение показателей
   

роста.

3. 
   Подтвердим выдвинутое предположение расчетом величины t-критерия Стьюдента, используя формулу (2.2.5).
   

^{|z̄| ⋅} √^{n ⋅ (n — 1)} t =

√^∑(z_i — z̄)<sup>2

|—4| ⋅</sup> √^{11 ⋅ (11 — 1)}


=
≈

√<sup>13

4 ⋅</sup> √¹¹⁰

3,61
≈ 11,62.

4. 
   Рассчитать число степеней свободы по формуле (2.2.6):
   

k= 2 (n – 1) = 2  (11-1) = 20.

5. 
   ^{Сравним расчетное значение t-критерия (t}ф^{= 11,62) с табличным значением} для k= 20 при  = 0,1% ( = 99,9%) (прилож. 1) и сделаем вывод.
   

^{Вывод:т.к. t}ф^{= 11,62  t}st^{= 3,85 для k= 20 при  = 0,1%, то с уверенностью }

= 99,9% можно говорить о том, что различия в показателях роста у исследуемых школьников в начале и конце учебного года достоверны.

Пример 2.2.6. Проведено измерение показателей кистевой динамометрии пра- вой и левой рук у 9 исследуемых. Определить достоверность различий методом Стьюдента в полученных результатах, если данные выборок таковы:

^{Правая рука: x}i<sup>, кГ 36; 29; 38; 35; 39; 42; 37; 38; 39.

Левая рука: y</sup>i^{, кГ 30; 32; 38; 26; 43; 35; 30; 32; 40.}

Решение.

1. 
   Данные тестирования заносим в рабочую таблицу и сделаем необходимые расчеты.
   

xi	yi	zi= (xi–yi)	(zi — z̄)	(zi — z̄)2
36	30	6	3	9
29	32	-3	-6	36
38	38	0	-3	9
35	26	9	6	36
39	43	-4	-7	49
42	35	7	4	16
37	30	7	4	16
38	32	6	3	9
39	40	-1	-4	16
x̄ =37	ȳ =34	z̄ =3		∑(zi — z̄)2 =196

2. 
   На основании расчета средних величин выборок выдвигаем рабочую гипотезу.
   

Рабочаягипотеза:т.к. x̄ =37 кГ  ȳ =34 кГ, то предположим, что у исследу- емых выше показатели кистевой динамометрии правой руки, чем левой.

3. 
   Подтвердим выдвинутое предположение расчетом величины t-критерия Стьюдента, используя формулу (2.2.5):
   

^{|z̄| ⋅} √^{n ⋅ (n — 1)} t =

√^∑(z_i — z̄)<sup>2


|3| ⋅</sup> √^{9 ⋅ (9 — 1)}


=


√<sup>196

3 ⋅</sup> √<sup>72

=</sup> 14
≈ 1,82.

4. 
   Рассчитаем число степеней свободы по формуле (2.2.6):
   

k= 2 (n – 1) = 2 (9 – 1) = 16.

5. 
   ^{Сравниваем расчетное значение t-критерия (t}ф^{= 1,82) с табличным значе- нием для k= 16 при}  ^{= 5% (} ^{= 95%) (прилож. 1) и сделаем вывод.}
   

^{Вывод:т.к. t}ф^{= 1,82  t}st^{= 2,12 для k= 16 при  = 95%, то можно говорить о}

том, что различия в показателях кистевой динамометрии правой и левой рук у ис- следуемой группы недостоверны.

Сравнениедвухвыборочныхдисперсийизнормальныхсовокупностей.

F-критерийФишера-Снедекора.

Для проверки гипотезы о равенстве генеральных дисперсий t-крите- рий оказывается недостаточно точным, особенно на малочисленных вы- борках. В поисках лучшего критерия Р.Э. Фишер нашел, что если две не- зависимые выборки получены из генеральных совокупностей Xи Yс оди-

наковыми дисперсиями σ² и σ², то при доказательстве предположения о

x y

том, что обе выборки независимы и получены из нормально распределен- ных генеральных совокупностей, вместо разности σ² – σ² лучше взять

x y

разность натуральных логарифмов этих величин (lnσ² – lnσ² ), где σ² 

x y1 x


y
 σ², то эта величина, обозначенная через Z, распределяется нормально не только при наличии больших, но и среднего объема совокупностей. При вычислении Zвместо натуральных логарифмов можно использовать де-

сятичные логарифмы, имея в виду, что Z= 2,3036(lgσ² –lgσ²), или Z=

x y

= 2,3026  lgσ² /σ², а также Z= 1,1513  lgσ² /σ², где σ²  σ².

x y x y x y

Д. Снедекор предложил вместо логарифма отношений использовать отношение выборочных дисперсий F(F-критерийиликритерийФишера-Снедекора):


σ
2


_σ2
F = ^x. (2.2.7)

y

Критерий F функционально связан с вероятностью, он имеет непре- рывную функцию распределения и зависит только от чисел степеней сво- боды: k₁ = n_х– 1 и k₂ = n_у– 1 сравниваемых дисперсий. Характерным для F оказывается то, что он полностью определяется выборочными диспер- сиями и не зависит от генеральных параметров, так как предполагается,

что обе дисперсии σ² и σ² из одной и той же генеральной совокупности.

x y

Поэтому при k  отношение σ²/σ²  1. График плотности вероятности

x y

F распределения для k₁ и k₂ и критических границ F₁ и F₂ приводится на рисунке 2.2.3. Видно, что распределение F при небольшом объеме вы- борки n имеет асимметричную форму, которая по мере увеличения числа испытаний (n) приближается к нормальной кривой.


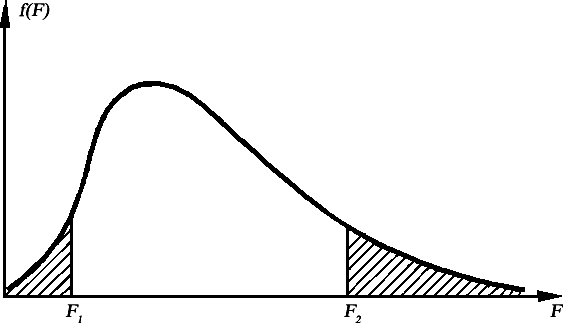
Рис. 2.2.3. График плотности вероятности F-распределения для типичных значений k₁ и k₂ числа степеней свободы

и критические границы F₁ и F₂.


σ
2


_σ2
Закономерность функции F = ¹ для двух уровней значимости р₁ = 0,05

2

и р₂ = 0,01 и соответствующих степеней свободы k₁ и k₂ табулирована в

виде критических (стандартных) значений критерия F (прил. 2). В этой таблице степени свободы для большей дисперсии берутся по горизонтали (верхняя строка), а по вертикали (первая графа) – степени свободы для меньшей дисперсии. При этом всегда берется отношение большей дис-

персии (σ²) к меньшей (σ²), поэтому F 1. В случае равенства значений

x y

дисперсий (σ² = σ²), величина F-критерия равна единице (F= 1). Чем

x y

значительнее расхождение между выборочными дисперсиями, тем больше будет величина F-критерия, и, наоборот, чем меньше разница

между дисперсиями σ² и σ², тем меньше окажется величина F-критерия.

x y

Нулевая гипотеза исходит из признания равенства дисперсий σ² = σ².

x y

Если эмпирические значения критерия Фишера (F_ф) меньше теоретиче- ских, указанных в таблице (F_st) для соответствующего уровня значимости и степеней свободы k₁ и k₂ (прилож. 2), они рассматриваются как случай- ные, различия между выборками не достоверны, т. е. они принадлежат к одной генеральной совокупности. Если же F_ф F_st, нулевая гипотеза от- вергается, разница между сравниваемыми величинами признается стати- стически достоверной, т. е. выборки взяты из разных совокупностей.